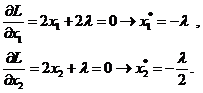Метод множителей лагранжа уравнение связи

Функция Лагранжа

Назначение сервиса . Онлайн-калькулятор используется для нахождения экстремума функции через множители Лагранжа в онлайн режиме (см. пример и пример решения графическим способом). При этом решаются следующие задачи:

1. составляется функция Лагранжа L(X) в виде линейной комбинации функции F(X) и ограничений g_i(x);
2. находятся частные производные функции Лагранжа, ∂L/∂x_i, ∂L/∂λ_i;
3. составляется система из (n + m) уравнений, ∂L/∂x_i = 0.
4. определяются переменные x_i и множители Лагранжа λ_i.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Метод множителей Лагранжа применяется как в линейном программировании, так и в нелинейном. В экономике этот метод используется в задаче потребительского выбора.

Правило множителей Лагранжа

Пример 1 . Методом множителей Лагранжа решить следующую задачу оптимизации:
min f(x) = x₁ 2 + x₂ 2
h₁(x) = 2x₁ + x₂ -2 = 0
Соответствующая задача оптимизации без ограничений записывается в следующем виде:
L(x, λ) = x₁ 2 + x₂ 2 + λ(2x₁ + x₂ – 2) → min
Решение:

Для того чтобы проверить, соответствует ли стационарная точка X минимуму, вычислим матрицу Гессе функции L(x, λ), рассматриваемой как функция от x,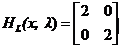
,
которая оказывается положительно определенной (2*2 – 0*0 = 4 > 0).
Это означает, что L(x, λ) – выпуклая функция. Следовательно, координаты x * = (-λ, λ/2) определяют точку глобального минимума. Оптимальное значение λ находится путем подстановки значений x₁ * и x₂ * в уравнение ограничений 2x₁ + x₂ -2 = 0, откуда вычисляем значение λ:
2λ + λ/2 = -2, откуда λ = -0.8
Таким образом, минимум достигается в точке x * с координатами x₁ * = 0.8 и x₂ * = 0.4. Значение ЦФ:
min f(x) = 0.8
Ответ: x * = [0.8; 0.4] T , f(x * ) = 0.8

Пример 2 . Исследовать на условный экстремум функцию f(x,y)_max = x 2 + 8xy+3y 2 при данных уравнениях связи.
9x +10y = 29

Условный экстремум. Метод множителей Лагранжа. Первая часть.

Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $\varphi (x,y)=0$.

Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $\varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=\psi(x)$, то подставив $y=\psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=f\left(x,\psi(x)\right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.

Метод множителей Лагранжа для функций двух переменных.

Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ (параметр $\lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:

Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_^<''>dx^2+2F_^<''>dxdy+F_^<''>dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F 0$, то $d^2F 0$, т.е. имеем условный минимум функции $z=f(x,y)$.

Примечание относительно формы записи определителя $H$. показать\скрыть

Некоторые авторы записывают определитель $H$ в иной форме (с знаком «-«):

В этой ситуации сформулированное выше правило изменится следующим образом: если $H > 0$, то функция имеет условный минимум, а при $H m$):

Обозначив множители Лагранжа как $\lambda_1,\lambda_2,\ldots,\lambda_m$, составим функцию Лагранжа:

Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:

Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F 0.$$

Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_<\max>=z(1;3)=10$.

Аналогично, в точке $M_2(-1;-3)$ найдем:

$$H=8\cdot\left| \begin 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end \right|= 8\cdot\left| \begin 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \end \right|=-40$$

Так как $H 0$. Следовательно, знак $H$ противоположен знаку $\lambda$. Можно и довести вычисления до конца:

Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:

Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $\left( dx \right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $\lambda_1=-\frac<1><2>$ получим $d^2F 0$, посему в данной точке функция имеет условный максимум, $z_<\max>=\frac<500><243>$.

Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:

Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

Так как $ d^2F \Bigr|_=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F \Bigr|_=-10 dx^2 0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_<\min>=u(0)=0$. Так как $u_^<''>(M_2) 0; \; y > 0. \end \right. $$

Все дальнейшие преобразования осуществляются с учетом $x > 0; \; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $\lambda=-\frac<5x>$ и подставим найденное значение в первое уравнение: $5y-\frac<5x>\cdot \frac<4>=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $\frac<4y^2><8>+\frac<2>-1=0$, $y^2=1$, $y=1$.

Так как $y=1$, то $x=2$, $\lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.

В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $\lambda=-10$, получив при этом:

Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:

Подставляя $x=2$, $y=1$, $\lambda=-10$, получим:

Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_<\max>=6$.

В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Условный экстремум

Понятие условного экстремума.

Пусть на открытом множестве \(G \subset \boldsymbol^\) заданы функции \(f_<0>(x)\), \(f_<1>(x), \ldots, f_(x)\), причем \(m Определение 1.

Точка \(x^ <0>= (x_<1>^<0>, \ldots, x_^<0>) \in G\) называется точкой условного минимума функции \(f_<0>(x)\) при наличии связей \eqref, если найдется такая окрестность \(S_<\delta>(x^<0>)\), что для всех \(x \in G \cap S_<\delta>(x^<0>)\) выполнено неравенство \(f_<0>(x) \geq f_<0>(x^<0>)\).

Точка \(x^ <0>\in G\) называется точкой строгого условного минимума функции \(f_<0>(x)\) при наличии связей \eqref, если найдется такая окрестность \(S_<\delta>(x^<0>)\), что для всех \(x \in \dot_<\delta>(x^<0>) \cap G\) выполнено неравенство \(f_<0>(x) \geq f_<0>(x^<0>)\).

Аналогично определяются точки условного максимума. Точки условного максимума и минимума называются точками условного экстремума.

Прямой метод отыскания точек условного экстремума.

Предположим, что из системы уравнений \eqref можно выразить какие-либо \(m\) переменных \(x_\) через остальные переменные. Тогда, подставив вместо соответствующих переменных \(x_\) их выражения через остальные \(n-m\) переменных в функцию \(f_<0>(x)\), получим функцию \(F\) от \(n-m\) переменных.

Задача о нахождении точек экстремума функции \(f_<0>(x)\) при наличии связей \eqref сведется к задаче нахождения обычного (безусловного) экстремума функции \(F\), зависящей от \(n-m\) переменных.

Найти точки условного экстремума функции \(z = 1-x^<2>-y^<2>\), если \(x+y = 1\).

\(\vartriangle\) Уравнение связи \(x+y = 1\) легко разрешается относительно переменной \(y\), а именно \(y = 1-x\). Подставив это выражение для \(y\) в функцию \(z = 1-x^<2>-y^<2>\), получаем, что \(z = 1-x^<2>-(1-x)^ <2>= 2x-2x^<2>\). Функция \(2x-2x^<2>\) имеет максимум при \(x = \frac<1><2>\). Точка \((\frac<1><2>, \frac<1><2>)\) является точкой условного максимума функции \(z(x, y)\) при наличии связи \(x+y = 1\), причем \(z_ <\max>= \displaystyle\frac<1><2>\). \(\blacktriangle\)

Прямой метод нахождения условного экстремума редко бывает эффективным ввиду трудности разрешения уравнений связей относительно какой-либо группы переменных.

Метод множителей Лагранжа.

Рассмотрим функцию \(n+m\) переменных
$$
L(x, \lambda) = f_<0>(x)+\lambda_<1>f_<1>(x)+\ldots+\lambda_f_(x),\nonumber
$$
где \(x \in G\), а \(\lambda = (\lambda_<1>, \ldots, \lambda_) \in \boldsymbol^\). Числа \(\lambda_<1>, \ldots, \lambda_\) называются множителями Лагранжа, а функция \(L(x, \lambda)\) называется функцией Лагранжа.

Пусть \(x^<0>\) — точка условного экстремума функции \(f_<0>(x)\) при наличии связей \eqref, и пусть функции \(f_(x)\), \(i = \overline<0, m>\), непрерывно дифференцируемы в окрестности точки \(x^<0>\), причем в точке \(x^<0>\) ранг матрицы Якоби
$$
A = \begin\displaystyle\frac<\partial f_<1>><\partial x_<1>>(x)&\ldots&\displaystyle\frac<\partial f_<1>><\partial x_>(x)\\………&…..&…….\\\displaystyle\frac<\partial f_><\partial x_<1>>(x)&\ldots&\displaystyle\frac<\partial f_><\partial x_>(x)\end\label
$$
равен \(m\).

Тогда найдутся такие множители Лагранжа \(\lambda_<1>^<0>, \ldots, \lambda_^<0>\), что \((x^0,\ \lambda^0)\) будет стационарной точкой функции Лагранжа.

\(\circ\) Так как \(m Теорема 2.

Пусть \(x^<0>\) есть точка условного минимума функции \(f_<0>(x)\) при наличии связей \eqref, и пусть функции \(f_(x)\), \(i = \overline<1, m>\), имеют непрерывные частные производные второго порядка в окрестности точки \(x^<0>\), причем в точке \(x^<0>\) ранг функциональной матрицы \eqref равен \(m\).

Тогда найдутся множители Лагранжа \(\lambda_<1>^<0>, \ldots, \lambda_^<0>\) такие, что \((x^<0>, \lambda^<0>)\) есть стационарная точка функции Лагранжа, a \(d^<2>L(x^<0>, \lambda^<0>) \geq 0\) при \((dx_<1>, \ldots, dx_) \in E_\).

\(\circ\) Так как выполнены все условия теоремы 1, то найдутся множители Лагранжа \(\lambda_<1>^<0>, \ldots, \lambda_^<0>\) такие, что \((x^<0>, \lambda^<0>)\) будет стационарной точкой функции Лагранжа, то есть выполняются условия \eqref. Повторяя рассуждения теоремы 1, рассмотрим сложную функцию \eqref, имеющую безусловный экстремум в точке \((x_^<0>, \ldots, x_^<0>)\). Так как эта функция имеет непрерывные частные производные второго порядка, то, в силу теоремы о необходимом условии минимума должно быть выполнено условие \(d^<2>F(x_^<0>, \ldots, x_^<0>) \geq 0\).

Воспользовавшись правилом нахождения второго дифференциала сложной функции и формулой \eqref, находим, что
$$
\sum_^ \sum_^ \frac <\partial^<2>f_<0>(x^<0>)> <\partial x_\partial x_> dx_ dx_+\sum_^ \frac <\partial^<2>f_<0>><\partial x_>(x^<0>) d^<2>x_ \geq 0.\label
$$

Если умножить каждое из равенств \eqref на соответствующий множитель Лагранжа \(\lambda_^<0>\) и сложить с неравенством \eqref, то получаем неравенство
$$
d_^<2>L(x^<0>, \lambda^<0>)+\sum_^ \frac<\partial L(x^<0>, \lambda^<0>)><\partial x_> d^<2>x_ \geq 0.\label
$$
Последняя сумма в неравенстве \eqref равна нулю, так как \((x^<0>, \lambda^<0>)\) есть стационарная точка функции Лагранжа и в ней выполняются условия \eqref. Таким образом, \(d_^<2>L(x^<0>, \lambda^<0>) \geq 0\) при \((dx_<1>, \ldots, dx_) \in E_\). \(\bullet\)

(Достаточные условия условного экстремума).

Пусть функции \(f_(x)\), \(i = \overline<0, m>\), имеют непрерывные частные производные второго порядка в окрестности точки \(x^ <0>\in \boldsymbol^\), причем в точке \(x^<0>\) ранг функциональной матрицы (3) равен \(m\), и пусть \((x^<0>, \lambda^<0>)\) есть стационарная точка функции Лагранжа \(L(x, \lambda)\).

Тогда если \(d_L(x^<0>, \lambda^<0>)\) есть положительно определенная квадратичная форма при \(dx \in E_\), то \(x^<0>\) является точкой условного строгого минимума функции \(f_<0>(x)\) при наличии связей \eqref. Если \(d_L(x^<0>, \lambda^<0>)\) есть отрицательно определенная квадратичная форма при \(dx \in E_\), то \(x^<0>\) — точка условного строгого максимума. Если \(d_L(x^<0>, \lambda^<0>)\) есть неопределенная квадратичная форма при \(dx \in E_\), то \(x^<0>\) не есть точна условного экстремума функции \(f_<0>(x)\) при наличии связей \eqref.

\(\circ\) Пусть
$$
E = \(x) = 0, i = \overline<1, m>\>.\label
$$
По условию теоремы функции \(f_(x)\), \(i = \overline<0, m>\), имеют непрерывные частные производные второго порядка, а ранг функциональной матрицы \eqref равен \(m\). Повторяя рассуждения теоремы 1, можем без ограничения общности считать, что выполнено условие \eqref и что найдется такая окрестность \(K(x^<0>) = K_<1>(x_<1>^<0>, \ldots, x_^<0>) \times K_<2>(x_^<0>, \ldots, x_^<0>)\), что множество \(E \cap K(x^<0>)\) можно задать формулой \eqref. На \(E \cap K(x^<0>)\) функция \(f_<0>(x)\) становится функцией \(n-m\) переменных \(F(x_^<0>, \ldots, x_^<0>)\), определенной формулой \eqref и имеющей непрерывные частные производные второго порядка.

Рассмотрим функцию \(L(x, \lambda^<0>)\) на множестве \(E \cap K(x^<0>)\). Очевидно, что
$$
L(x, \lambda^<0>) = f_<0>(x) = F(x_, \ldots, x_)\ \mbox<при>\ x \in E \cap K(x^<0>).\label
$$
В силу инвариантности формы первого дифференциала из формулы \eqref следует, что
$$
dF(x_^<0>, \ldots, x_^<0>) = d_L(x^<0>, \lambda^<0>) = 0.\label
$$

Пусть \(d_^<2>L(x^<0>, \lambda^<0>) > 0\) при \(dx \in E_\), \(dx \neq 0\). Так как множество \(E \cap K(x^<0>)\) можно задать в форме \eqref, то, выбирая \(dx_, \ldots, dx_\) произвольным образом, получим, что дифференциалы \(dx_<1>,…, dx_\) зависят от \((dx_, \ldots, dx_)\). Дифференцируя тождества \eqref в точке \(x^<0>\), получаем соотношения \eqref, которые означают, что \(dx \in E_\).

Из \eqref и \eqref получаем, что \((x_^<0>, \ldots, x_^<0>)\) есть точка строгого минимума функции \(F(x_, \ldots, x_)\), то есть \(x^<0>\) есть точка строгого минимума функции \(f_<0>(x)\) на множестве \(E \cap K(x^<0>)\). Таким образом, \(x^<0>\) есть точка строгого условного минимума функции \(f_<0>(x)\) при наличии связей \eqref.

Аналогично рассматривается случай, когда \(d_^<2>L(x^<0>, \lambda^<0>) Замечание.

Если окажется, что \(d_^<2>L(x^<0>, \lambda^<0>)\) есть положительно определенная квадратичная форма на всем пространстве \(\boldsymbol^\), то \(d_^<2>L(x^<0>, \lambda^<0>) > 0\) при \(dx \in E_\), \(dx \neq 0\). Поэтому в этом случае в квадратичной форме \(d_^<2>L(x^<0>, \lambda^<0>)\) не нужно исключать зависимые дифференциалы.

Найти экстремумы функции \(x-2y+2z = u\) и на сфере \(x^<2>+y^<2>+z^ <2>= 1\).

\(\vartriangle\) Строим функцию Лагранжа
$$
L(x, y, z, \lambda) = x-2y+2z+\lambda(x^<2>+y^<2>+x^<2>-1)\nonumber
$$
Стационарные точки функции Лагранжа находим, решая систему уравнений
$$
\frac<\partial L> <\partial x>= 1+2\lambda x = 0,\quad \frac<\partial L> <\partial y>= -2+2\lambda y = 0,\quad \frac<\partial L> <\partial z>= 2+2\lambda z = 0,\nonumber
$$
$$
\frac<\partial L> <\partial \lambda>= x^<2>+y^<2>+z^<2>-1 = 0.\nonumber
$$
Исключая из этой системы \(x, y, z\), получаем \(\displaystyle\left(\frac<1><2\lambda>\right)^<2>+\left(\frac<1><\lambda>\right)^<2>+\left(\frac<1><\lambda>\right)^<2>-1 = 0\), откуда \(\lambda_ <1>= \displaystyle\frac<3><2>\), \(\lambda_ <2>= -\displaystyle\frac<3><2>\).

У функции Лагранжа есть две стационарные точки,
$$
M_ <1>= \left(-\frac<1><3>, \frac<2><3>, -\frac<2><3>, \frac<3><2>\right)\quad \mbox<и>\quad M_ <2>= \left(\frac<1><3>, -\frac<2><3>, \frac<2><3>, -\frac<3><2>\right).\nonumber
$$

Так как \(d^<2>L(M_<1>) = 3(dx^<2>+dy^<2>+dz^<2>) > 0\), a \(d^<2>L(M_<2>) = -3(dx^<2>+dy^<2>+dz^<2>) 0\), тo \(\displaystyle\left(-\frac<1><3>, \frac<2><3>, -\frac<2><3>, \frac<3><2>\right)\) — точка условного минимума, a \(\displaystyle\left(\frac<1><3>, -\frac<2><3>, \frac<2><3>, -\frac<3><2>\right)\) — точка условного максимума функции \(u = x-2y+2x\) при наличии ограничения \(x^<2>+y^<2>+z^<2>-1 = 0\), Причем \(u_ <\min>= -3\), \(u_ <\max>= 3\). \(\blacktriangle\)

Найти условные экстремумы функции \(f_<0>(x, y) = e^\), \(a \neq 0\), при наличии ограничения \(f_(x, y) = x^<3>+y^<3>+x+y-4 = 0\).

\(\vartriangle\) Построим функцию Лагранжа:
$$
L(x, y) = e^+\lambda(x^<3>+y^<3>+x+y-4).\nonumber
$$
Стационарные точки функции Лагранжа определяются из системы уравнений
$$
\begin
& \displaystyle\frac<\partial L> <\partial x>= aye^+\lambda(3x^<2>+1) = 0,\\
&\\
& \displaystyle\frac<\partial L> <\partial y>= axe^+\lambda(3y^<2>+1) = 0,\\
&\\
& \displaystyle\frac<\partial L> <\partial \lambda>= x^<3>+y^<3>+x+y-4 = 0.
\end\label
$$

Умножая первое уравнение на \(x\), а второе на \(y\) и вычитая, получаем
$$
\lambda(3x^<3>-3y^<3>+x-y) = \lambda(x-y)(3x^<2>+3xy+3y^<2>+1) = 0.\label
$$

Если \(\lambda = 0\), то из первых двух уравнений \eqref получаем \(x = y = 0\). Но \(x = y = 0\) не удовлетворяет уравнению связи. Итак, \(\lambda \neq 0\), поэтому из \eqref следует, что \(x = y\) (второй сомножитель всегда положителен: \(3(x^<2>+xy+y^<2>)+1 > 0\)). Подставляя \(x = y\) в уравнение связи, получаем \(x^<3>+x = 2\), \(x = y = 1\). Первое из уравнений \eqref дает при \(x = y = 1\) значение \(\lambda = -\displaystyle\frac <4>e^\).

Поэтому при \(a 0\) — условный максимум функции \(f_<0>(x, y)\) при наличии связи \(x^<3>+y^<3>+x+y = 4\), причем экстремальное значение функции равно \(e^\). \(\blacktriangle\)

Уравнение связи \(x^<3>+y^<3>+x+y = 4\) было бы затруднительно разрешить относительно одной из переменных. Метод Лагранжа для примера 2 более эффективен, чем прямой метод исключения зависимых переменных.

Несколько замечаний о методе множителей Лагранжа.

Задачи об отыскании экстремумов функций (как числовых, так и функций более общей природы) при наличии ограничений являются весьма распространенными. Теория экстремальных задач интенсивно развивается и находит широкий круг приложений. Здесь были рассмотрены ограничения типа равенств, задаваемые достаточно гладкими функциями (гладкие связи). Метод множителей Лагранжа имеет глубокие обобщения и на более общий случай, когда ограничения задаются системой равенств и неравенств при помощи недифференцируемых в обычном смысле функций.

В конкретных прикладных вопросах множители Лагранжа имеют содержательную интерпретацию. Так, в механике множители Лагранжа задают реакции связей, а в математической экономике — цены на продукты производства. Широко развиты приближенные методы решения экстремальных задач, использующие современную вычислительную технику.