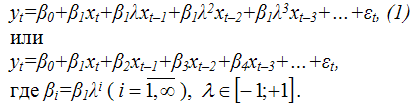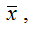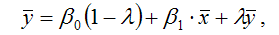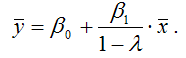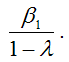Алгоритм Левенберга — Марквардта для нелинейного метода наименьших квадратов и его реализация на Python
Нахождение экстремума(минимума или максимума) целевой функции является важной задачей в математике и её приложениях(в частности, в машинном обучении есть задача curve-fitting). Наверняка каждый слышал о методе наискорейшего спуска (МНС) и методе Ньютона (МН). К сожалению, эти методы имеют ряд существенных недостатков, в частности — метод наискорейшего спуска может очень долго сходиться в конце оптимизации, а метод Ньютона требует вычисления вторых производных, для чего требуется очень много вычислений.
Для устранения недостатков, как это часто бывает, нужно глубже погрузиться в предметную область и добавить ограничения на входные данные. В частности: МНС и МН имеют дело с произвольными функциями. В статистике и машинном обучении часто приходится иметь дело с методом наименьших квадратов (МНК). Этот метод минимизирует сумму квадрата ошибок, т.е. целевая функция представляется в виде
Алгоритм Левенберга — Марквардта является нелинейным методом наименьших квадратов. Статья содержит:
- объяснение алгоритма
- объяснение методов: наискорейшего спуска, Ньтона, Гаусса-Ньютона
- приведена реализация на Python с исходниками на github
- сравнение методов
В коде использованы дополнительные библиотеки, такие как numpy, matplotlib. Если у вас их нет — очень рекомендую установить их из пакета Anaconda for Python
Зависимости
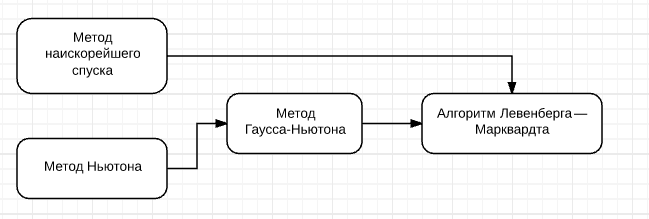
Алгоритм Левенберга — Марквардта опирается на методы, приведённые в блок-схеме
Поэтому, сначала, необходимо изучить их. Этим и займёмся
Определения
— наша целевая функция. Мы будем минимизировать
. В этом случае,
является функцией потерь
— градиент функции
в точке
—
, при котором
является локальным минимумом, т.е. если существует проколотая окрестность
, такая что
— глобальный минимум, если
, т.е.
не имеет значений меньших, чем
— матрица Якоби для функции
в точке
. Т.е. это таблица всех частных производных первого порядка. По сути, это аналог градиента для
, так как в этом случае мы имеем дело с отображением из
-мерного вектора в
-мерный, поэтому нельзя просто посчитать первые производные по одному измерению, как это происходит в градиенте. Подробнее
— матрица Гессе (матрица вторых производных). Необходима для квадратичной аппроксимации
Выбор функции
В математической оптимизации есть функции, на которых тестируются новые методы.
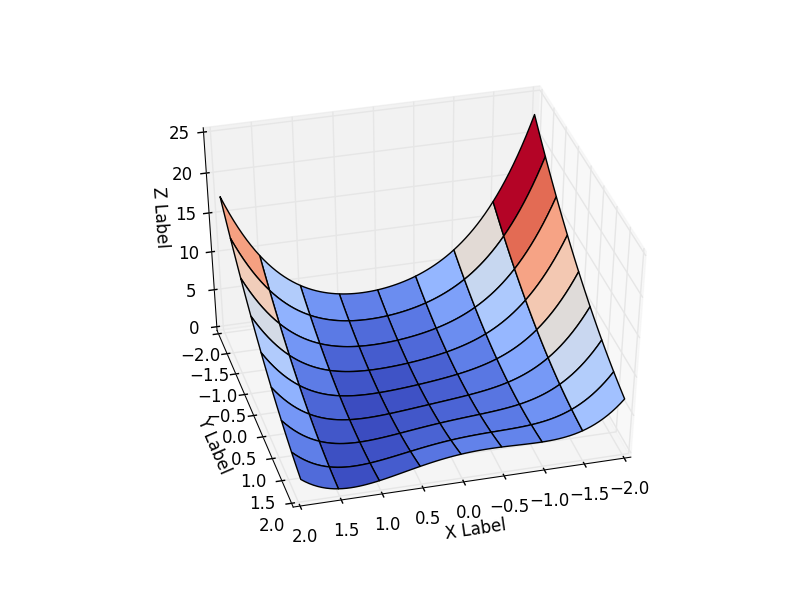
Одна из таких функция — Функция Розенброка. В случае функции двух переменных она определяется как
Я принял . Т.е. функция имеет вид:
Будем рассматривать поведение функции на интервале
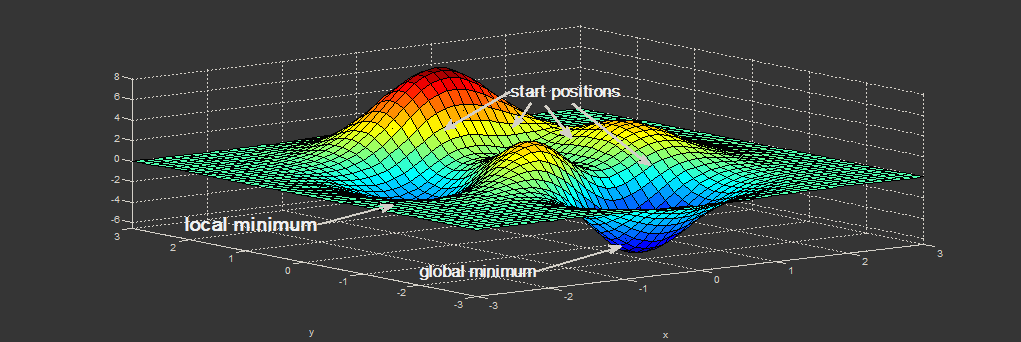
Эта функция определена неотрицательно, имеет минимум
В коде проще инкапсулировать все данные о функции в один класс и брать класс той функции, которая потребуется. Результат зависит от начальной точки оптимизации. Выберем её как . Как видно из графика, в этой точке функция принимает наибольшее значение на интервале.
Метод наискорейшего спуска(Steepest Descent)
Сам метод крайне прост. Принимаем , т.е. целевая функция совпадает с заданной.
Нужно найти — направление наискорейшего спуска функции
в точке
.
может быть линейно аппроксимирована в точке
:
где — угол между вектором
.
следует из скалярного произведения
Так как мы минимизируем , то чем больше разница в
, тем лучше. При
выражение будет максимально(
, норма вектора всегда неотрицательна), а
будет только если вектора
будут противоположны, поэтому
Направление у нас верное, но делая шаг длиной можно уйти не туда. Делаем шаг меньше:
Теоретически, чем меньше шаг, тем лучше. Но тогда пострадает скорость сходимости. Рекомендуемое значение
В коде это выглядит так: сначала базовый класс-оптимизатор. Передаём всё, что понадобится в дальнейшем( матрицы Гессе, Якоби, сейчас не нужны, но понадобятся для других методов)
Код самого оптимизатора:
| Итерация | X | Y | Z |
|---|---|---|---|
| 25 | 0.383 | -0.409 | 0.334 |
| 75 | 0.693 | 0.32 | 0.058 |
| 532 | 0.996 | 0.990 |
Бросается в глаза: как быстро шла оптимизация в 0-25 итерациях, в 25-75 уже медленне, а в конце потребовалось 457 итераций, чтобы приблизиться к нулю вплотную. Такое поведение очень свойственно для МНС: очень хорошая скорость сходимости вначале, плохая в конце.
Метод Ньютона
Сам Метод Ньютона ищет корень уравнения, т.е. такой , что
. Это не совсем то, что нам нужно, т.к. функция может иметь экстремум не обязательно в нуле.
А есть ещё Метод Ньютона для оптимизации. Когда говорят о МН в контексте оптимизации — имеют в виду его. Я сам, учась в институте, спутал по глупости эти методы и не мог понять фразу «Метод Ньютона имеет недостаток — необходимость считать вторые производные».
Рассмотрим для
Принимаем , т.е. целевая функция совпадает с заданной.
Разлагаем в ряд Тейлора, только в отличии от МНС нам нужно квадратичное приближение:
Несложно показать, что если , то функция не может иметь экстремум в
. Точка
называется стационарной.
Продифференцируем обе части по . Наша цель, чтобы
, поэтому решаем уравнение:
— это направление экстремума, но оно может быть как максимумом, так и минимумом. Чтобы узнать — является ли точка
минимумом — нужно проанализировать вторую производную. Если
0$, то $f(x+d_н)»/> является локальным минимумом, если
— максимумом.
В многомерном случае первая производная заменяется на градиент, вторая — на матрицу Гессе. Делить матрицы нельзя, вместо этого умножают на обратную(соблюдая сторону, т.к. коммутативность отсутствует):
Аналогично одномерному случаю — нужно проверить, правильно ли мы идём? Если матрица Гессе положительно определена, значит направление верное, иначе используем МНС.
| Итерация | X | Y | Z |
|---|---|---|---|
| 25 | -1.49 | 0.63 | 4.36 |
| 75 | 0.31 | -0.04 | 0.244 |
| 179 | 0.995 | -0.991 |
Сравните с МНС. Там был очень сильный спуск до 25 итерации( практически упали с горы), но потом сходимость сильно замедлилась. В МН, напротив, мы сначала медленно спускаемся с горы, но затем движемся быстрее. У МНС ушло с 25 по 532 итерацию, чтобы дойти до нуля с . МН же оптимизировал
за 154 последних итераций.
Это частое поведение: МН обладает квадратичной скоростью сходимости, если начинать с точки, близкой к локальному экстремуму. МНС же хорошо работает далеко от экстремума.
МН использует информацию кривизны, что было видно на рисунке выше(плавный спуск с горки).
Ещё пример, демонстрирующий эту идею: на рисунке ниже красный вектор — это направление МНС, а зелёный — МН
[Нелинейный vs линейный] метод наименьших квадратов
В МНК у нас есть модель , имеющая
параметров, которые настраиваются так, чтобы минимизировать
, где —
-е наблюдение.
В линейном МНК у нас есть $m$ уравнений, каждое из которых мы можем представить как линейное уравнение
Для линейного МНК решение единственно. Существуют мощные методы, такие как QR декомпозиция, SVD декомпозиция, способные найти решение для линейного МНК за 1 приближённое решение матричного уравнения .
В нелинейном МНК параметр может сам быть представлен функцией, например
. Так же, может быть произведение параметров, например
и т.д.
Здесь же приходится находить решение итеративно, причём решение зависит от выбора начальной точки.
Методы ниже имеют дело как раз с нелинейным случаем. Но, сперва, рассмотрим нелиненый МНК в контексте нашей задачи — минимизации функции
Ничего не напоминает? Это как раз форма МНК! Введём вектор-функцию
и будем подбирать так, чтобы решить систему уравнений(хотя бы приближённо):
Тогда нам нужна мера — насколько хороша наша аппроксимация. Вот она:
Я применил обратную операцию: подстроил вектор-функцию под целевую
. Но можно и наоборот: если дана вектор-функция
, строим
из (5). Например:
Напоследок, один очень важдный момент. Должно выполняться условие , иначе методом пользоваться нельзя. В нашем случае условие выполняется
Метод Гаусса-Ньютона
Метод основан на всё той же линейной аппроксимации, только теперь имеем дело с двумя функциями:
Далее делаем то же, что и в методе Ньютона — решаем уравнение(только для ):
Несложно показать, что вблизи :
Результат превысил мои ожидания. Всего за 3 итерации мы пришли в точку . Чтобы продемонстрировать траекторию движения я уменьшил learningrate до 0.2
Алгоритм Левенберга — Марквардта
Он основан на одной из версий Методе Гаусса-Ньютона( «damped version» ):
называется параметром регулизации. Иногда
заменяют на
для улучшения сходимости.
Диагональные элементы будут положительны, т.к. элемент
матрицы
является скалярным произведением вектора-строки
в
на самого себя.
Для больших получается метод наискорейшего спуска, для маленьких — метод Ньютона.
Сам алгоритм в процессе оптимизации подбирает нужный на основе gain ratio, определяющийся как:
Если 0″/>, то
— хорошая аппроксимация для
, иначе — нужно увеличить
.
Начальное значение задаётся как
, где
— элементы матрицы
.
рекомендовано назначать за
. Критерием остановки является достижение глобального минимуму, т.е.
В оптимизаторах я не реализовывал критерий остановки — за это отвечает пользователь. Мне нужно было только движение к следующей точке.
Результат получился тоже хороший:
| Итерация | X | Y | Z |
|---|---|---|---|
| 0 | -2 | -2 | 22.5 |
| 4 | 0.999 | 0.998 | |
| 11 | 1 | 1 | 0 |
При learningrate =0.2:
Сравнение методов
| Название метода | Целевая функция | Достоинства | Недостатки | Сходимость |
|---|---|---|---|---|
| Метод наискорейший спуск | дифференцируемая | -широкий круг применения -простая реализация -низкая цена одной итерации | -глобальный минимум ищется хуже, чем в остальных методах -низкая скорость сходимости вблизи экстремума | локальная |
| Метод Нютона | дважды дифференцируемая | -высокая скорость сходимости вблизи экстремума -использует информацию о кривизне | -функция должны быть дважды дифференцируема -вернёт ошибку, если матрица Гессе вырождена ( не имеет обратной) -есть шанс уйти не туда, если находится далеко от экстремума | локальная |
| Метод Гаусса-Нютона | нелинейный МНК | -очень высокая скорость сходимости -хорошо работает с задачей curve-fitting | -колонки матрицы J должны быть линейно-независимы -налагает ограничения на вид целевой функции | локальная |
| Алгоритм Левенберга — Марквардта | нелинейный МНК | -наибольная устойчивость среди рассмотренных методов -наибольшие шансы найти глобальный экстремум -очень высокая скорость сходимости(адаптивная) -хорошо работает с задачей curve-fitting | -колонки матрицы J должны быть линейно-независимы -налагает ограничения на вид целевой функции -сложность в реализации | локальная |
Несмотря на хорошие результаты в конкретном примере рассмотренные методы не гарантируют глобальную сходимость(найти которую — крайне трудная задача). Примером из немногих методов, позволяющих всё же достичь этого, является алгоритм basin-hopping
Совмещённый результат(специально понижена скорость последних двух методов):
Нелинейный метод наименьших квадратов. Метод Койка
Если модель с распределенным лагом характеризуется бесконечной величиной максимального лага L, то для оценивания неизвестных параметров данной модели применяются нелинейный метод наименьших квадратов и метод Койка. При этом исходят из предположения о геометрической структуре лага, т. е. влияние лаговых значений факторной переменной на результативную переменную уменьшается с увеличением величины лага в геометрической прогрессии.
Если в модель включена только одна объясняющая переменная, то её можно представить в виде:
В модели с распределённым лагом (1) неизвестными являются три параметра: β0, β1 и λ. Найти оценки данных параметров с помощью традиционного метода наименьших квадратов невозможно по нескольким причинам, поэтому в данном случае используются нелинейный метод наименьших квадратов и метод Койка
Суть нелинейного метода наименьших квадратов заключается в том, что для параметра
λ определяются значения в интервале [-1;+1] с определённым шагом, например, 0,05 (чем меньше шаг, тем точнее будет результат).
Для каждого значения λ рассчитывается переменная z:
с таким значением лага L, при котором дальнейшие лаговые значения переменной x не оказывают существенного влияния на z.
На следующем этапе с помощью традиционного метода наименьших квадратов оценивается модель регрессии вида:
и рассчитывается коэффициент детерминации R 2 . Данный процесс осуществляется для всех значений λ из интервала [-1;+1]. Оценками коэффициентов β0, β1 и λ будут те, которые обеспечивают наибольшее значение R 2 для модели регрессии (2).
В основе метода или преобразования Койка лежит предположение о том, что если модель регрессия (1) справедлива для момента времени t, то она справедлива и для момента времени (t–1):
Умножим обе части данного уравнения на λ и вычтем их из модели регрессии (1). В результате получим выражение вида:
Полученная модель (2) является моделью авторегрессии, что позволяет проанализировать её краткосрочные и долгосрочные динамические свойства.
Значение переменной yt–1в краткосрочном периоде (в текущем периоде) рассматривается как фиксированное, а воздействие переменной х на переменную у характеризует коэффициент β1.
Если xtв долгосрочном периоде (без учёта случайной компоненты модели) стремится к некоторому равновесному значению
то yt и yt–1также будут стремиться к своему равновесному значению, которое вычисляется по формуле:
из чего следует:
Долгосрочное влияние переменной х на переменную у характеризуется коэффициентом
Несмотря на то, что метод Койка очень удобен в вычислительном отношении (оценки параметров β0, β1 и λ можно рассчитать с помощью традиционного метода наименьших квадратов), оценки, полученные с его помощью, будут смещёнными и несостоятельными, т. к. нарушается первое условие нормальной линейной модели регрессии.
Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
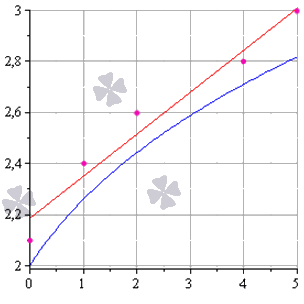
Как изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
http://be5.biz/ekonomika/e008/98.html
http://zaochnik.com/spravochnik/matematika/stati/metod-naimenshih-kvadratov/