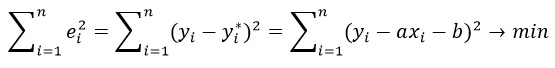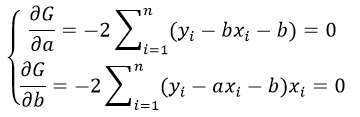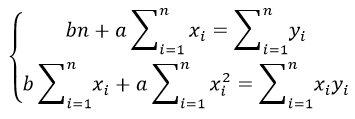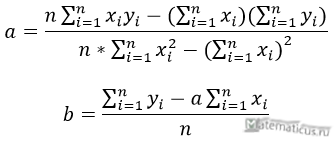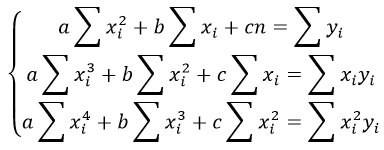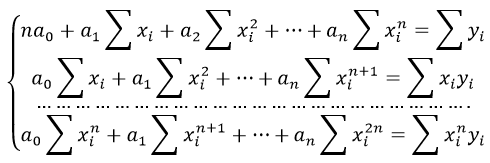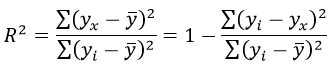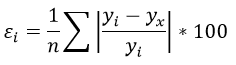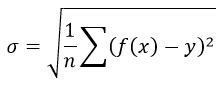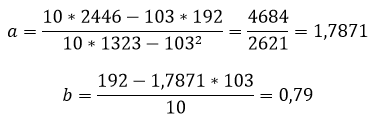Метод наименьших квадратов регрессия
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R 2 :
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
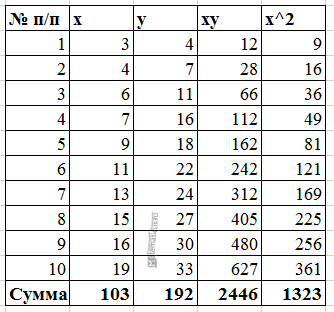
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
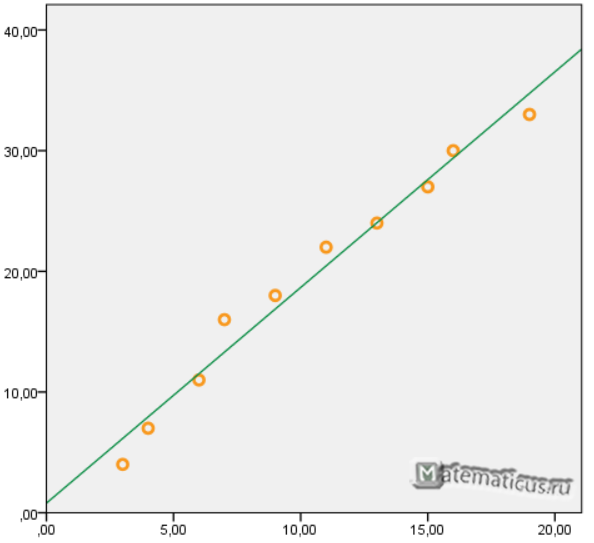
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
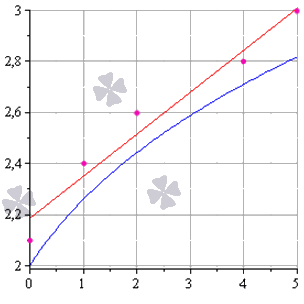
Как изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
Математика для машинного обучения: линейная регрессия и регрессия наименьших квадратов
Дата публикации Mar 21, 2018
Машинное обучение — это все о математике, хотя сегодня доступно много библиотек, которые могут применять сложные формулы с помощью вызова функции, любой способ желательно изучить хотя бы основы этого, чтобы лучше понять его.
Давайте попробуем понять линейную регрессию и регрессию наименьших квадратов простым способом.
Что такое линейная регрессия?
Линейная регрессия — это прогнозирующий алгоритм, который обеспечивает линейную связь междупрогнозирование(Назови это«Y») а такжевход(Звонок‘ИКС’).
Как мы знаем из основной математики, если мы построим«X»,»Y»На графике линейные отношения всегда будут иметь прямую линию. Например, если мы строим график этих значений
Это будет идеально прямая линия
Прежде чем углубляться в это, давайте поймем тот факт, что в реальной жизни мы не получаем такой идеальной взаимосвязи между входами и прогнозами, и поэтому нам нужны алгоритмы машинного обучения.
Уравнение прямой из 2 точек
Уравнение прямой записывается с использованием y = mx + b , где m это склон (градиент) и b является y-перехват (где линия пересекает ось Y).
После того, как мы получим уравнение прямой из 2 точек в пространстве в y = mx + b формат, мы можем использовать одно и то же уравнение для прогнозирования точек при различных значениях x что приводит к прямой линии.
В этой формуле m это склон и b это у-перехват.
Линейная регрессия — это способ предсказать ‘Y’ значения для неизвестных значений ввода ‘X’ нравится 1.5, 0.4, 3.6, 5.7 и даже для -1, -5, 10 и т.п.
Давайте рассмотрим пример из реальной жизни, чтобы продемонстрировать использование линейной регрессии и использование метода наименьших квадратов для уменьшения ошибок.
Линейная регрессия на примере реального мира
Давайте рассмотрим реальный пример цен на сельскохозяйственную продукцию и ее изменения в зависимости от места продажи. Цена будет низкой при покупке напрямую у фермеров и высокой при доставке из центра города.
Учитывая этот набор данных, мы можем предсказать цену продукта в промежуточных точках
Когда набор данных используется для прогнозов, он также называется Обучающим набором данных
В этом примере, если мы рассмотрим ввод ‘X — Axis’ как место продажи и ‘Y — Axis’ как цена (представьте любую валюту, с которой вы знакомы), мы можем построить график как
Постановка задачи
Учитывая этот набор данных, спрогнозируйте цену сельскохозяйственной продукции, если она продается в промежуточных точках между домом фермера и городом в центре города.
Учебный набор данных
Приведенный выше набор данных можно рассматривать в качестве Обучающего набора данных для вышеуказанной постановки задачи. Если мы рассматриваем эти входные данные в качестве Обучающих данных для модели, мы можем использовать эту модель для прогнозирования цены в местах между
- Фермеры дома — деревня
- Деревня — Город
- Город — Город
- Город — City Downtown
Наша цель — получить прямую линию, которая минимизирует ошибку между данными обучения и нашей моделью прогнозирования, когда мы рисуем линию, используя уравнение прямой линии.
Уравнение прямой (y = mx + b)
Математика позволяет нам получить прямую линию между любыми двумя (x,y) точки в двухмерном графе. В этом примере давайте рассмотрим фермерский дом и цену в качестве отправной точки, а город в центре — в качестве конечной точки.
Координаты начальной и конечной точек будут
где x представляет местоположение и y представлять цену.
Первый шаг заключается в том, чтобы придумать формулу в виде y = mx + b где x известная ценность и y это прогнозируемое значение.
Рассчитать прогноз y для любого входного значения x у нас есть два неизвестных, m = slope(Gradient) а также b = y-intercept(also called bias)
Наклон (m = изменение в y / изменение в x)
Наклон линии рассчитывается как изменение y делится на изменение x, поэтому расчет будет выглядеть
Y-перехват / смещение рассчитывается по формуле y-y1 = m(x-x1)
Как только мы пришли к нашей формуле, мы можем проверить то же самое, подставив x как для начальной, так и для конечной точек, которые использовались для расчета формулы, поскольку она должна обеспечивать y ценность.
Теперь мы знаем, что наша формула верна, поскольку мы получаем то же самое y значение путем замены x значение, но как насчет других значений x между 2,3,4 , Давайте разберемся
Эти значения отличаются от того, что было на самом деле в обучающем наборе (понятно, что исходный график не был прямой линией), и если мы построим это (x,y) график против исходного графика, прямая линия будет далеко от исходных точек на графике x=2,3, and 4
Тем не менее, первый шаг успешен, так как нам удалось предсказать Y для неизвестных значений X
Минимизация ошибки
Ошибка определяется как разница значений между фактическими точками и точками на прямой линии). В идеале, мы хотели бы иметь прямую линию, где ошибка минимизирована во всех точках.
Существует множество математических способов сделать то же самое, и один из методов называется регрессией по методу наименьших квадратов.
Наименьшая площадь регрессии
Регрессия наименьших квадратов — это метод, который минимизирует ошибку таким образом, чтобы минимизировать сумму всех квадратических ошибок. Вот шаги, которые вы используете для расчета регрессии наименьших квадратов.
Во-первых, формула для расчета m = slope является
Примечание: ** 2 означает квадрат, синтаксис Python
Итак, давайте вычислим все значения, необходимые для определения наклона (m), сначала начнем с вычисления значений с x
Теперь давайте посчитаем значения с y
Наличие этих значений позволяет нам рассчитать сумму всех
(x — xmean)*(y — ymean)
Теперь давайте вычислим знаменательную часть уравнения, которое
Sum of (x — xmean)**2
Таким образом, общий расчет будет
Расчет y-перехвата
Y-перехват рассчитывается по формуле b = ymean — m * xmean
Общая формула теперь может быть записана в виде y = mx + b как
Использование регрессии наименьших квадратов для значений X, Y
Давайте посмотрим, как прогноз y меняется, когда мы применяем y = 19.2x + (-22.4) на все значения х.
Давайте нарисуем этот конкретный линейный график по отношению к стандартным значениям.
Как мы видим, эти значения ближе к реальной линии по сравнению с прямыми значениями прямой линии между начальной и конечной точками. Если мы сравним это с линейным графиком, мы визуализируем разницу
Почему этот метод называется регрессией по методу наименьших квадратов?
Этот метод предназначен для уменьшения квадрата суммы всех значений ошибок. Чем ниже ошибка, тем меньше общее отклонение от исходной точки. Мы можем сравнить то же самое с ошибками, сгенерированными по прямой линии, а также с регрессией наименьших квадратов
Как мы видим, метод наименьших квадратов дает лучшие результаты, чем простая прямая линия между двумя точками расчета.
Метод наименьших квадратов — не единственные методы, используемые в машинном обучении для улучшения модели, есть другие, о которых я расскажу в следующих постах.
http://zaochnik.com/spravochnik/matematika/stati/metod-naimenshih-kvadratov/
http://www.machinelearningmastery.ru/mathematics-for-machine-learning-linear-regression-least-square-regression-de09cf53757c/