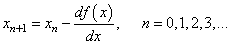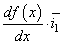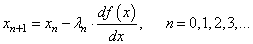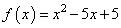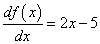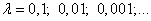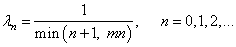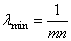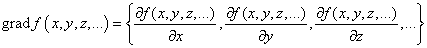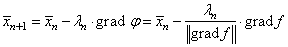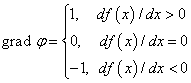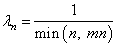Метод наискорейшего спуска система нелинейных уравнений

5.2. Метод градиента (метод скорейшего спуска)

Пусть имеется система нелинейных уравнений:

(5.13)

Систему (5.13) удобнее записать в матричном виде:

(5.14)

Где — вектор – функция; — вектор – аргумент.

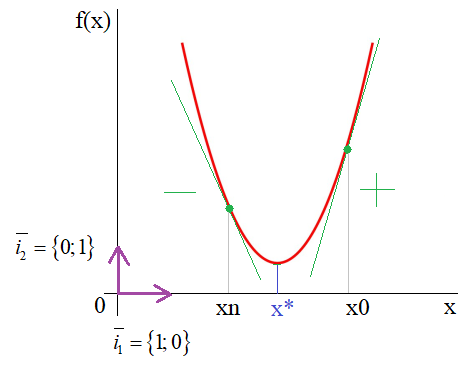
Решение системы (5.14), как и для системы линейных уравнений (см. п. 3.8), будем искать в виде

(5.15)

Здесь и — векторы неизвестных на P и P+1 шагах итераций; вектор невязок на P-ом шаге – F(P) = F(X(P)); W‘P – транспонированная матрица Якоби на P – ом шаге;

;

.

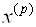
Пример 5.2. Методом градиента вычислим приближенно корни системы

Расположенные в окрестности начала координат.

Выберем начальное приближение:

По вышеприведенным формулам найдем первое приближение:

Аналогичным образом находим следующее приближение:

Ограничимся двумя итерациями (шагами), и оценим невязку:

· Как видно из примера, решение достаточно быстро сходится, невязка быстро убывает.

· При решении системы нелинейных уравнений методом градиента матрицу Якоби необходимо пересчитывать на каждом шаге (итерации).

Вопросы для самопроверки

· Как найти начальное приближение: а) для метода Ньютона; б) для метода градиента?

· В методе скорейшего спуска вычисляется Якобиан (матрица Якоби). Чем отличается Якобиан, вычисленный для СЛАУ, от Якобиана, вычисленного для нелинейной системы уравнений?

· Каков критерий остановки итерационного процесса при решении системы нелинейных уравнений: а) методом Ньютона; б) методом скорейшего спуска?

Julia, Градиентный спуск и симплекс метод

Продолжаем знакомство с методами многомерной оптимизации.

Далее предложена реализация метода наискорейшего спуска с анализом скорости выполнения, а также имплементация метода Нелдера-Мида средствами языка Julia и C++.

Метод градиентного спуска

Поиск экстремума ведется шагами в направлении градиента (max) или антиградиента (min). На каждом шаге в направлении градиента (антиградиента) движение осуществляется до тех пор, пока функция возрастает (убывает).

За теорией пройдитесь по ссылкам:

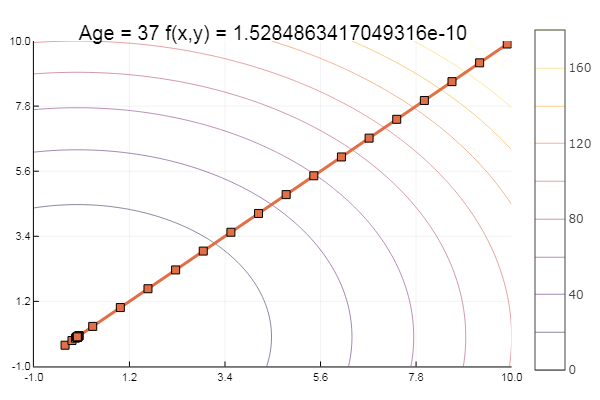
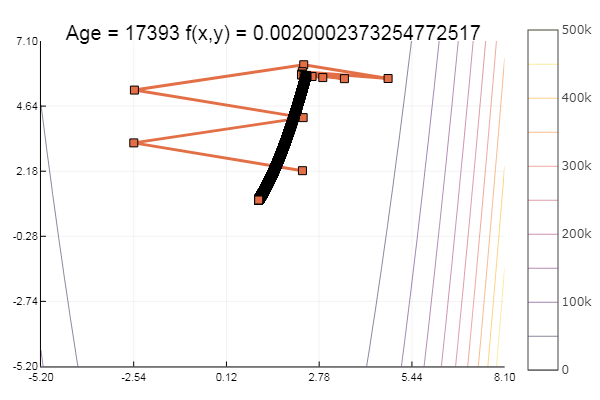
Модельной функцией выберем эллиптический параболоид и зададим функцию отрисовки рельефа:

Зададим функцию реализующую метод наискорейшего спуска, которая принимает размерность задачи, точность, длину шага, начальное приближение и размеры рамки ограничивающей график:

На функции вычисляющей направление градиента можно заостриться в плане оптимизации.

Первое, что идет на ум — это действия с матрицами:

Чем действительна хороша Julia, так это тем, что проблемные места легко можно потестить:

Можно кинуться перепечатывать всё в Сишном стиле

Но как оказывается, оно само и без нас знает, какие типы надо ставить, так что приходим к компромиссу:

А теперь пусть рисует:

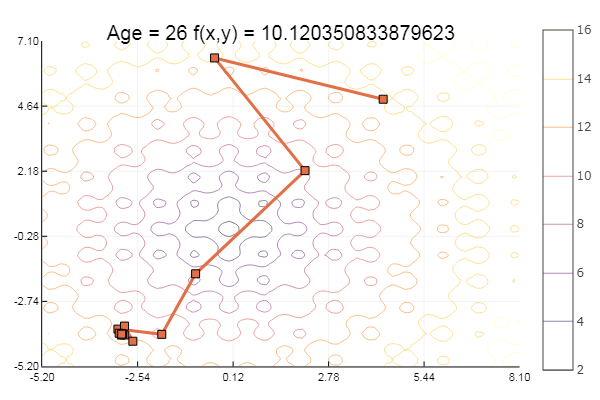
А теперь опробуем на функции Экли:

Свалилось в локальный минимум. Сделаем-ка шаги побольше:

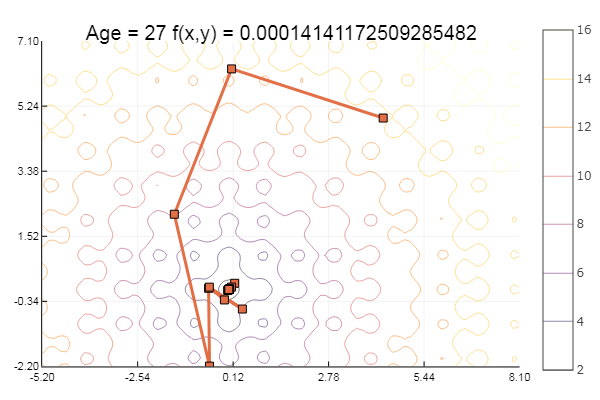
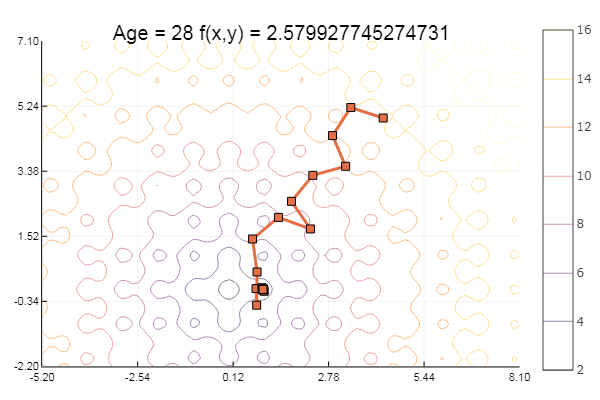
Отлично! А теперь что-нибудь с оврагом, например функцию Розенброка:

Мораль: градиенты не любят пологостей.

Симплекс метод

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной(точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс.

И сам симплекс метод:

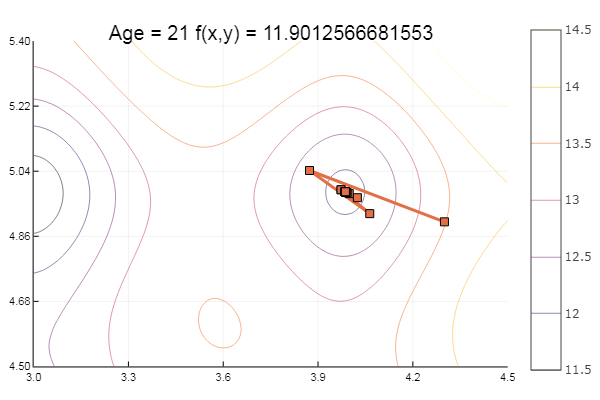
И на десерт какую-нибудь буку… например функцию Букина

Локальный минимум — ну ничего, главное правильно подобрать стартовый симплекс, так что для себя я нашел фаворита.

Бонус. Методы Нелдера-Мида, наискорейшего спуска и покоординатного спуска на С++

На сегодня достаточно. Следующим этапом будет логично попробовать что-нибудь из глобальной оптимизации, набрать побольше тестовых функций, а затем изучить пакеты со встроенными методами.

Метод градиентного спуска

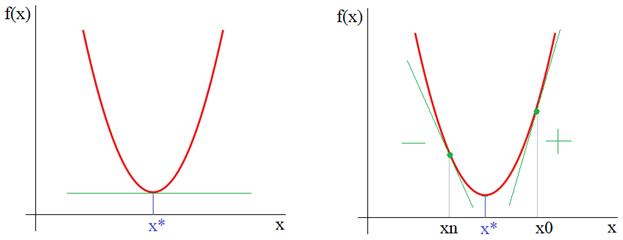
На этом занятии мы с вами рассмотрим довольно популярный алгоритм под названием «метод градиентного спуска» или, еще говорят «метод наискорейшего спуска». Идея метода довольно проста. Предположим, имеется дифференцируемая функция 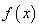с точкой экстремума x*. Нам нужно найти эту точку. Для простоты восприятия информации, предположим, что это парабола с точкой экстремума x*. Конечно, для такого простого случая эту точку можно очень легко определить из уравнения:

но она используется лишь для визуализации метода градиентного спуска. В действительности функции могут быть гораздо сложнее и зависеть от произвольного числа аргументов, для которых решать системы уравнений достаточно хлопотное занятие. Или же, функция постоянно меняется и нам необходимо под нее подстраиваться для определения текущего положения точки минимума. Все эти задачи удобнее решать с позиции алгоритмов направленного поиска, например, градиентного спуска.

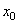
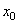
Итак, из рисунка мы хорошо видим, что справа от точки экстремума x* производная положительна, а слева – отрицательна. И это общее математическое правило для точек локального минимума. Предположим, что мы выбираем произвольную начальную точку на оси абсцисс. Теперь, смотрите, чтобы из двигаться в сторону x*, нам нужно в области положительных производных ее уменьшать, а в области отрицательных – увеличивать. Математически это можно записать так:

Здесь n – номер итерации работы алгоритма. Но, вы можете спросить: а где же тут градиент? В действительности, мы его уже учли чисто интуитивно, когда определяли перемещение вдоль оси абсцисс для поиска оптимальной точки x*. Но математика не терпит такой вульгарности, в ней все должно быть прописано и точно определено. Как раз для этого нужно брать не просто производную, а еще и определять направление движения, используя единичные векторы декартовой системы координат:

И градиент функции 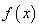можно записать как

то есть, это будет уже направление вдоль оси ординат и направлен в сторону наибольшего увеличения функции. Соответственно, двигаясь в противоположную сторону, будем перемещаться к точке минимума x*.

Конечно, в результирующей формуле алгоритма поиска этот единичный вектор не пишется, а вместо него указывается разность по оси ординат, т.к. именно вдоль нее он и направлен:

Однако у такой формулы есть один существенный недостаток: значение производной может быть очень большим и мы попросту «перескочим» через значение x* и уйдем далеко влево или вправо. Чтобы этого не происходило, производную дополнительно умножают на некоторое небольшое число λ:

которое, в общем случае, также может меняться от итерации к итерации. Этот множитель получил название шаг сходимости.

Давайте, для примера, реализуем этот алгоритм на Python для случая одномерной параболы. Вначале подключим необходимые библиотеки и определим две функции: параболу

и ее производную:

Затем, определим необходимые параметры алгоритма и сформируем массивы значений по осям абсцисс и ординат:

Далее, переходим в интерактивный режим работы с графиком, чтобы создать анимацию для перемещения точки поиска минимума и создаем окно с осями графика:

Отображаем начальный график:

Запускаем алгоритм градиентного поиска:

В конце выводим найденное значение аргумента и оставляем график на экране устройства:

После запуска увидим скатывание точки к экстремуму функции. Установим значение

Увидим «перескоки» оптимального значение, то есть, неравномерную сходимость к точки минимума. А вот, если поставить параметр

то скатывания совсем не будет, т.к. аргумент x будет «перескакивать» точку минимума и никогда ее не достигать. Вот так параметр λ влияет на работу алгоритма градиентного спуска.

Выбор шага сходимости

Важно правильно его подбирать в каждой конкретной решаемой задаче. Обычно, это делается с позиции «здравого смысла» и опыта разработчика, но общие рекомендации такие: начинать со значения 0,1 и уменьшать каждый раз на порядок для выбора лучшего,

который обеспечивает и скорость и точность подбора аргумента x. В целом, это элемент творчества и, например, можно встретить и такой вариант изменения шага сходимости:

Функция min здесь выбирает наименьшее из двух аргументов и использует его в знаменателе дроби. Это необходимо, чтобы величина шага при больших n не становилась слишком маленькой и ограничивалась величиной

где mn – некоторое заданное ограничивающее значение.

Еще один прием связан с нормализацией градиента на каждом шаге работы алгоритма. В этом случае градиент функции (то есть, вектор):

приводится к единичной норме:

И уже он используется в алгоритме наискорейшего спуска:

В одномерном случае нашего примера, это, фактически означает, что вместо действительного значения градиента, берутся числа ±1:

И алгоритм в Python примет вид:

Как видите, такой подход требует уменьшения величины шага сходимости, на последующих итерациях, например, так:

Результат выглядит уже лучше и при этом, мы не привязаны к значению градиента.

Локальный минимум

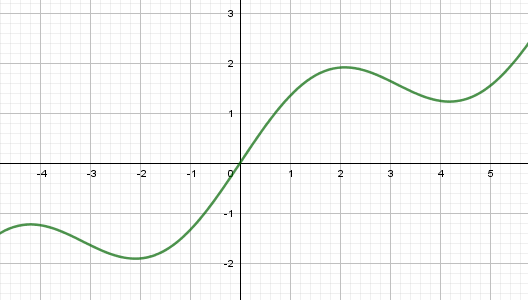
Еще одной особенностью работы этого алгоритма является попадание в область локального минимума функции. Например, если взять вот такой график:

То при начальном значении x=0 получим один минимум, а, например, при x=2,5 – другой. В этом легко убедиться, если в нашей программе переписать функции:

(последняя – это производная: ). Увеличим диапазон отображения графика:

и запустим программу. Теперь, установим начальное значение xx=2,5, снова запустим и увидим уже другую точку локального минимума.

Это, наверное, основной недостаток данного алгоритма – попадание в локальный минимум. Чтобы решить эту проблему перебирают несколько разных начальных значений и смотрят: при котором был достигнуто наименьшее значение. Его и отбирают в качестве результата. Такой ход не дает нам гарантии, что действительно был найден глобальный минимум функции (иногда он может не существовать, как, например, с нашей синусоидой), но, тем не менее, это повышает наш шанс найти лучшее решение. Вот базовая теория и практика применения метода наискорейшего спуска.

Видео по теме

#1: Метод наименьших квадратов

#2: Метод градиентного спуска

#3: Метод градиентного спуска для двух параметров

#4: Марковские процессы в дискретном времени

#5: Фильтр Калмана дискретного времени

#6: Фильтр Калмана для авторегрессионого уравнения

#7: Векторный фильтр Калмана

#8: Фильтр Винера

#9: Байесовское построение оценок, метод максимального правдоподобия

#10: Байесовский классификатор, отношение правдоподобия

© 2022 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта