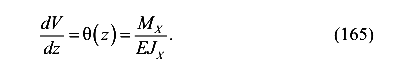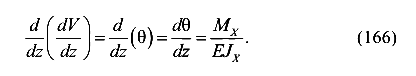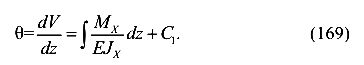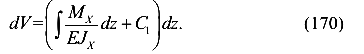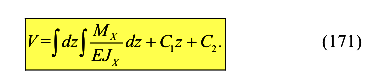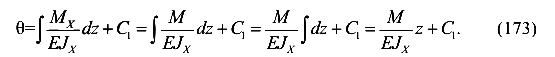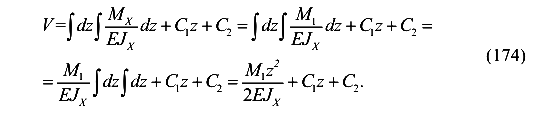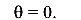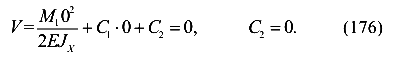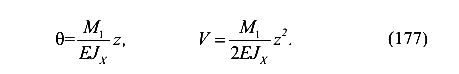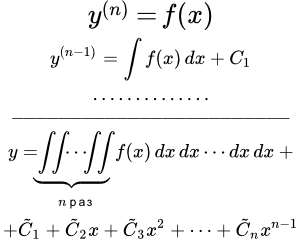Метод непосредственного интегрирования дифференциального уравнения

Метод интегрирования дифференциального уравнения изгиба балки

Наиболее естественным методом определения функции прогибов является метод непосредственного интегрирования уравнения изгибающих моментов.

$EI\,y»(x) = M(x)$ – полученное дифференциальное уравнение;

$EI\,y'(x) = EI\,\varphi (x) = \int dx + C$ – первый интеграл (уравнение углов поворота);

$EI\,y(x) = \int dx = \iint dxdx + C\,x + D$ – второй интеграл (уравнение прогибов).

Кроме интегрирования уравнения изгибающих моментов $M(x)$, для получения уравнения прогибов необходимо определить две постоянных интегрирования $C$ и $D$ из условий закрепления балки. При этом надо учесть, что шарнирная опора исключает прогибы балки, а жесткое зажатие – прогибы и углы поворота (то есть они равны нулю).

Физический смысл постоянных интегрирования такой: при $x = 0$ угол поворота $EI\,\varphi (0) = C$, а прогиб $EI\,y(0) = D$, то есть константа $C$ равна углу поворота в начале координат, константа $D$ равна прогибу балки при x=0.

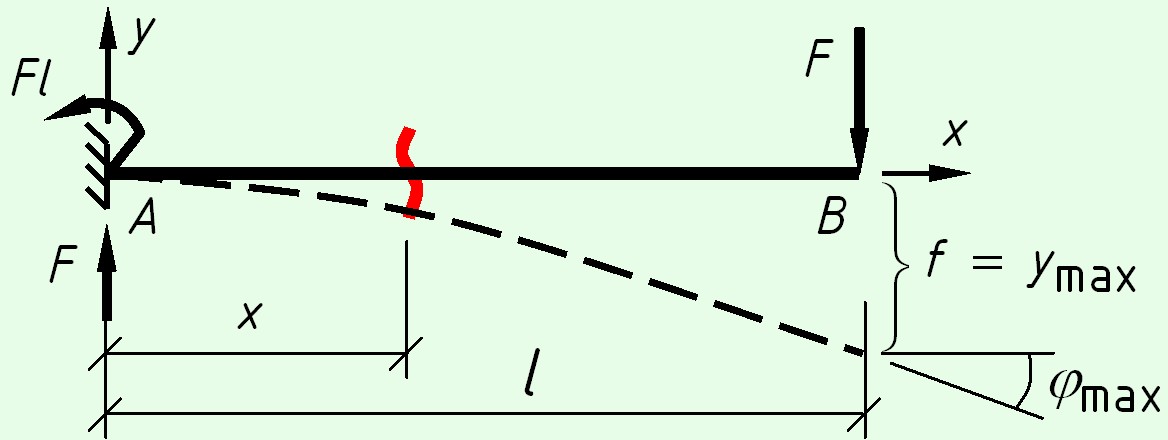
Консольная балка с силой на конце

На левой опоре возникают реакции – вертикальная сила $F$ и момент $M = F \cdot l$.

Уравнения изгибающих моментов

$M(x) = — Fl + Fx = F(x — l)$

Уравнение углов поворота

$EI\,y'(x) = EI\,\varphi (x) = \int dx + C = F(\frac<<>> <2>— lx) + C$

Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений

$\left\ < \beginEI\,\varphi (0) = F(\frac<<<0^2>>> <2>— l \cdot 0) + C = 0 \hfill \\ EI\,y(0) = F(\frac<<<0^3>>> <6>— l\frac<<<0^2>>><2>) + C \cdot 0 + D = 0. \hfill \\ \end \right.$

Решение этой системы уравнений приводит к результату $C = 0$, $D = 0$.

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l$

где знак « – » указывает направление перемещений – в сторону, противоположную положительному направлению оси $y$. Стрела прогиба $f = \frac<>><<3\,EI>>$.

Максимальный угол поворота сечения также будет иметь место при $x = l$

знак « – » указывает направление угла поворота – сечение поворачивается по часовой стрелке.

Шарнирно закрепленная балка с силой посередине

На опорах возникают вертикальные реакции $ = = F/2$.

Поскольку уравнение изгибающих моментов разное на двух разных участках, функция прогибов также будет разная. Используя полную симметрию расчетной схемы, далее будем рассматривать только левый участок, для которого уравнение изгибающих моментов имеет вид

$M(x) = \frac<2>x$, то есть $EI\,y»(x) = \frac<2>x$, интегрируем дважды

Константы интегрирования $C$ и $D$ полученного уравнения справедливы только для первого участка, поэтому их необходимо определять из условий, связанных с перемещениями на первом участке. Такими условиями является равенство нулю прогибов на опоре $A$ ($x = 0$) и, исходя из симметрии, равенство нулю угла поворота под силой $F$ ($x = l/2$). Имеем систему уравнений

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l/2$

Максимальные углы поворота сечений будут на опорах ($x = 0$ и $x = l$).

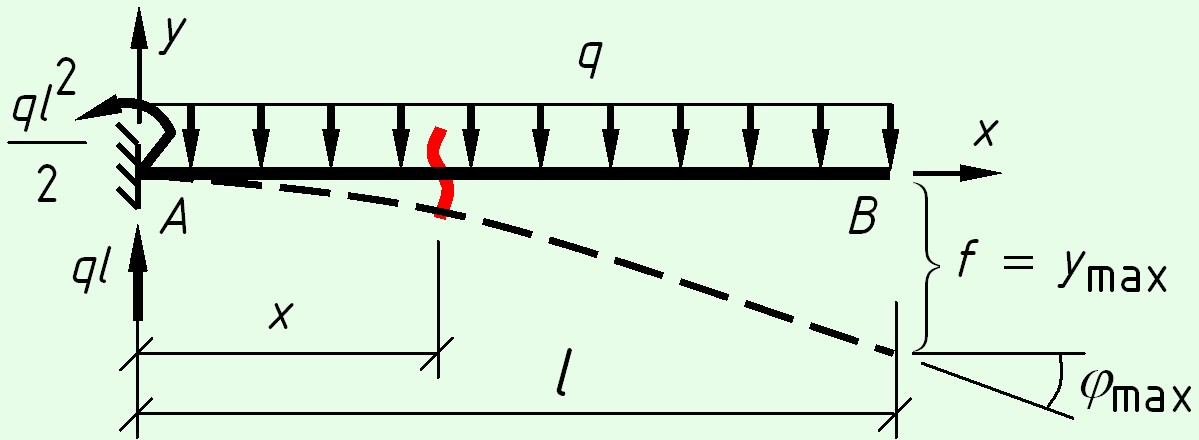
Консольная балка с равномерно распределенной нагрузкой

На левой опоре возникают реакции – вертикальная сила $ql$ и момент $M = \frac<>><2>$.

$M(x) = — \frac<>> <2>+ ql \cdot x — \frac<>><2>$, дважды интегрируем

Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений

$\left\ < \beginEI\,y'(0) = F(\frac<<<0^2>>> <2>— l \cdot 0) + C = 0 \hfill \\ EI\,y(0) = F(\frac<<<0^3>>> <6>— l\frac<<<0^2>>><2>) + C \cdot 0 + D = 0. \hfill \\ \end \right.$

Решение системы уравнений приводит к результату $C = 0$, $D = 0$.

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l$

Максимальный угол поворота сечения также будет иметь место при $x = l$

Метод непосредственного интегрирования

Метод непосредственного интегрирования

Метод основан на непосредственном интегрировании полученного приближенного дифференциального уравнения. Последовательно интегрируем дифференциальное уравнение (163). Вначале запишем его так

Учитываем, что первая производная от прогиба является функцией угла поворота поперечных сечений

Подставляем выражение (165) в уравнение (164) и получим

Проинтегрируем левую и правую части уравнения (167)

Выразим угол поворота через прогибы

Проинтегрируем левую и правую части уравнения и получим решение

Постоянные интегрирования 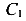и определяются из граничных условий на концах каждого участка балки. Число постоянных интегрирования равно удвоенному числу участков на балке. В этом недостаток рассматриваемого метода. Достоинством метода является возможность определения углов поворота и прогибов балки переменной жесткости и при любой по сложности нагрузке.

Пример:

Определение прогиба и угла поворота сечения балки методом непосредственного интегрирования. Рассмотрим защемленную балку постоянной жесткости (рис.63).

Изгибающий момент выражается функцией

Определим постоянные интегрирования. Для этого используем условие на концах балки:

1) при z = 0,

2) при z = 0, V=0.

В результате получим аналитические выражения (функции) для углов поворота и прогибов балки.

Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:

Дополнительные страницы которые вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Дифференциальное уравнение y (n) = f(x)

Общее решение

Рассмотрим дифференциальное уравнение n-го порядка, в котором n-я производная равна функции от независимой переменной x :
(1) .
Оно решается непосредственным интегрированием.
;
;

;
;

;
;
. . . . . . . .

.
Заменим постоянные интегрирования:
.
Тогда
(2) .
В результате мы получили общее решение (2) уравнения (1). Оно представляет собой сумму n-кратного повторного интеграла и многочлена степени .

Таким образом, если нас интересует общее решение уравнения (1), то мы должны проинтегрировать функцию n раз, и прибавить многочлен степени , коэффициентами которого являются постоянные интегрирования.

Частное решение с заданными начальными условиями

Если нас интересует задача Коши с заданными начальными условиями
(3) ,
то соответствующее частное решение имеет следующий вид:
(4)
.
См. «Решение дифференциального уравнения y (n) =f(x) с заданными начальными условиями».

Применение формулы Коши для повторных интегралов

Входящий в (4) n-кратный интеграл можно свести к однократному, если воспользоваться формулой Коши для повторных интегралов:
(5) .
Тогда решение уравнения (1) с начальными условиями (3) примет более простой вид:
(6)
.

Вывод формулы Коши (5) изложен на странице «Формула Коши для повторных интегралов». Здесь мы покажем, что функция , определяемое по формуле (6), удовлетворяет дифференциальному уравнению (1).

Выполняя n – 1 дифференцирований, получаем:
.
Дифференцируя еще раз, приходим к уравнению (1):
.

Пример

Найти общее решение уравнения:
.

Разделим исходное уравнение на . При получаем уравнение вида (1):
.

Преобразуем постоянные интегрирования:
.

Автор: Олег Одинцов . Опубликовано: 16-07-2013 Изменено: 19-11-2020