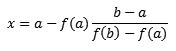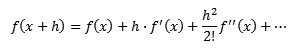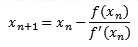Метод ньютона система нелинейные уравнения паскаль

Решение нелинейных уравнений на языке программирования Pascal

Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Из этой статьи вы узнаете о наиболее известных алгоритмах численного решения уравнений. Практически все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.

Наиболее простым в реализации является метод бисекции, или как его еще называют, метод половинного деления. Это итерационный метод, суть которого заключается в том, что на каждой итерации интервал сокращается вдвое до тех пор, пока не будет найдено решение с заданной точностью.

Данный метод достаточно прост и содержит всего два действия. Сначала находится переменная х – середина интервала [a,b]. После чего вычисляется значение функции в середине интервала. Затем определяется, совпадает ли по знаку значение функции в середине интервала, со знаком функции в левой части. В случаи если их знаки равны, то новой левой границей считается середина интервала, в ином же случаи правой граница интервала считается его середина. Таким образом, при каждой итерации интервал сокращается вдовое то справа, то слева. Очень часто можно встретить следующую реализацию данного метода.

Этот вариант, хотя и очень прост для понимания, содержит один недостаток. Дело в том, что если функция очень сильно изменяется, то при заданной точности, её значение может очень сильно отличаться. Поэтому для исключения этой неточности выгоднее использовать цикл с постусловием и сравнивать с заданным значением точности не разницу границ интервала, а значение функции. Тогда реализация метода примет следующий вид.

Другим очень хорошим методом нахождения корней уравнения, который несколько сложнее в реализации, чем предыдущий, является метод хорд. Отличается он тем, что границы интервала соединяются прямой линией, то есть хордой. Затем определяется точка пересечения этой прямой с осью абсцисс, по формуле:

После чего находится значение функции в точке пересечения. По аналогии с предыдущим методом определяется новая левая или правая граница интервала, которой является точка пересечения. Реализация данного метода на языке программирования Pascal может быть представлена следующим образом.

Еще одним хорошим методом решения уравнений является метод касательных или метод Ньютона. Главное его отличие от представленных ранее методов биссекции и хорд – отсутствие необходимости отделения корня. Вместо этого нужно задать лишь начальное приближение. Однако его главным недостатком остается сложность реализации, связанная, прежде всего с необходимостью определять производные исходного уравнения.

В основе метода Ньютона лежит разложения функции в ряд Тейлора:

Обычно значения ряда, содержащие шаг h во второй и более высоких степенях отбрасывают, так как их влияние на результат незначительны.

Суть метода заключается в экстраполяции функции касательными. После того как пользователь задает начальное приближение, программа должна определить точку пересечения касательной к графику функции с осью абсцисс. Для этого используется формула:

Затем находится значение функции в точке пересечения касательной с осью абсцисс и если получившиеся значение близко к нулю, то считается, что решение уравнения найдено. Реализация данного метода может быть представлена следующим образом

К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.

Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.

Метод ньютона система нелинейные уравнения паскаль

Pers.narod.ru. Алгоритмы. Метод Ньютона решения нелинейного уравнения

В литературе называется также методом касательных.

Рассмотрим графическую иллюстрацию метода (рис. 1). Предположим, что графическим методом определено начальное приближение х₀ к корню. В точке х₀ вычислим левую часть решаемого уравнения f₀ = f(x₀), а также производную в этой точке f'(x₀) = tg α. Следующее приближение к корню найдем в точке х₁, где касательная к функции f(x), проведенная из точки (х₀, f₀), пересекает ось абсцисс. Затем считаем точку х₁ в качестве начальной и продолжаем итерационный процесс. Из рис. видно, что таким способом можно приближаться к корню х*. При этом с каждой итерацией расстояние между очередным х_k+1 и предыдущим х_k приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выполнится условие

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10 -5 — 10 -6 достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и её производной.

Можно, несколько уменьшив скорость сходимости, ограничиться вычислением производной f'(x) только на первой итерации, а затем вычислять лишь значения f(x), не изменяя производной f'(x). Это алгоритм так называемого модифицированного метода Ньютона (рис. 2).

Ниже приводится простая консольная программа на Паскале для решения алгебраического уравнения произвольной степени n>1 . Функция f(x) и первая производная f'(x) задаются подпрограммами-функциями f и f1 соответственно.

Нелинейные системы и уравнения

В более общем случае мы имеем не одно уравнение (1), а систему нелинейных уравнений $$ \begin \tag <2>f_i(x_1, x_2, \ldots, x_n) = 0, \quad i = 1, 2, \ldots n. \end $$ Обозначим через \( \mathbf = (x_1, x_2, \ldots, x_n) \) вектор неизвестных и определим вектор-функцию \( \mathbf(\mathbf) = (f_1(\mathbf), f_2(\mathbf), \ldots, f_n(\mathbf)) \). Тогда система (2) записывается в виде $$ \begin \tag <3>\mathbf(\mathbf) = 0. \end $$ Частным случаем (3) является уравнение (1) (\( n = 1 \)). Второй пример (3) — система линейных алгебраических уравнений, когда \( \mathbf (\mathbf) = A \mathbf — \mathbf \).

Метод Ньютона

Решение нелинейных уравнений

При итерационном решении уравнений (1), (3) задается некоторое начальное приближение, достаточно близкое к искомому решению \( x^* \). В одношаговых итерационных методах новое приближение \( x_ \) определяется по предыдущему приближению \( x_k \). Говорят, что итерационный метод сходится с линейной скоростью, если \( x_ — x^* = O(x_k — x^*) \) и итерационный метод имеет квадратичную сходимость, если \( x_ — x^* = O(x_k — x^*)^2 \).

В итерационном методе Ньютона (методе касательных) для нового приближения имеем $$ \begin \tag <4>x_ = x_k + \frac, \quad k = 0, 1, \ldots, \end $$

Вычисления по (4) проводятся до тех пор, пока \( f(x_k) \) не станет близким к нулю. Более точно, до тех пор, пока \( |f_(x_k)| > \varepsilon \), где \( \varepsilon \) — малая величина.

Простейшая реализация метода Ньютона может выглядеть следующим образом:

Чтобы найти корень уравнения \( x^2 = 9 \) необходимо реализовать функции

Данная функция хорошо работает для приведенного примера. Однако, в общем случае могут возникать некоторые ошибки, которые нужно отлавливать. Например: пусть нужно решить уравнение \( \tanh(x) = 0 \), точное решение которого \( x = 0 \). Если \( |x_0| \leq 1.08 \), то метод сходится за шесть итераций.

Теперь зададим \( x_0 \) близким к \( 1.09 \). Возникнет переполнение

Возникнет деление на ноль, так как для \( x_7 = -126055892892.66042 \) значение \( \tanh(x_7) \) при машинном округлении равно \( 1.0 \) и поэтому \( f^\prime(x_7) = 1 — \tanh(x_7)^2 \) становится равной нулю в знаменателе.

Проблема заключается в том, что при таком начальном приближении метод Ньютона расходится.

Еще один недостаток функции naive_Newton заключается в том, что функция f(x) вызывается в два раза больше, чем необходимо.

Учитывая выше сказанное реализуем функцию с учетом следующего:

1. обрабатывать деление на ноль
2. задавать максимальное число итераций в случае расходимости метода
3. убрать лишний вызов функции f(x)

Метод Ньютона сходится быстро, если начальное приближение близко к решению. Выбор начального приближение влияет не только на скорость сходимости, но и на сходимость вообще. Т.е. при неправильном выборе начального приближения метод Ньютона может расходиться. Неплохой стратегией в случае, когда начальное приближение далеко от точного решения, может быть использование нескольких итераций по методу бисекций, а затем использовать метод Ньютона.

При реализации метода Ньютона нужно знать аналитическое выражение для производной \( f^\prime(x) \). Python содержит пакет SymPy, который можно использовать для создания функции dfdx . Для нашей задачи это можно реализовать следующим образом:

Решение нелинейных систем

Идея метода Ньютона для приближенного решения системы (2) заключается в следующем: имея некоторое приближение \( \pmb^ <(k)>\), мы находим следующее приближение \( \pmb^ <(k+1)>\), аппроксимируя \( \pmb(\pmb^<(k+1)>) \) линейным оператором и решая систему линейных алгебраических уравнений. Аппроксимируем нелинейную задачу \( \pmb(\pmb^<(k+1)>) = 0 \) линейной $$ \begin \tag <5>\pmb(\pmb^<(k)>) + \pmb(\pmb^<(k)>)(\pmb^ <(k+1)>— \pmb^<(k)>) = 0, \end $$ где \( \pmb(\pmb^<(k)>) \) — матрица Якоби (якобиан): $$ \pmb<\nabla F>(\pmb^<(k)>) = \begin \frac<\partial f_1(\pmb^<(k)>)> <\partial x_1>& \frac<\partial f_1(\pmb^<(k)>)> <\partial x_2>& \ldots & \frac<\partial f_1(\pmb^<(k)>)> <\partial x_n>\\ \frac<\partial f_2(\pmb^<(k)>)> <\partial x_1>& \frac<\partial f_2(\pmb^<(k)>)> <\partial x_2>& \ldots & \frac<\partial f_2(\pmb^<(k)>)> <\partial x_n>\\ \vdots & \vdots & \ldots & \vdots \\ \frac<\partial f_n(\pmb^<(k)>)> <\partial x_1>& \frac<\partial f_n(\pmb^<(k)>)> <\partial x_2>& \ldots & \frac<\partial f_n(\pmb^<(k)>)> <\partial x_n>\\ \end $$ Уравнение (5) является линейной системой с матрицей коэффициентов \( \pmb \) и вектором правой части \( -\pmb(\pmb^<(k)>) \). Систему можно переписать в виде $$ \pmb(\pmb^<(k)>)\pmb <\delta>= — \pmb(\pmb^<(k)>), $$ где \( \pmb <\delta>= \pmb^ <(k+1)>— \pmb^ <(k)>\).

Таким образом, \( k \)-я итерация метода Ньютона состоит из двух стадий:

1. Решается система линейных уравнений (СЛАУ) \( \pmb(\pmb^<(k)>)\pmb <\delta>= -\pmb(\pmb^<(k)>) \) относительно \( \pmb <\delta>\).

2. Находится значение вектора на следующей итерации \( \pmb^ <(k+1)>= \pmb^ <(k)>+ \pmb <\delta>\).

Для решения СЛАУ можно использовать приближенные методы. Можно также использовать метод Гаусса. Пакет numpy содержит модуль linalg , основанный на известной библиотеке LAPACK, в которой реализованы методы линейной алгебры. Инструкция x = numpy.linalg.solve(A, b) решает систему \( Ax = b \) методом Гаусса, реализованным в библиотеке LAPACK.

Когда система нелинейных уравнений возникает при решении задач для нелинейных уравнений в частных производных, матрица Якоби часто бывает разреженной. В этом случае целесообразно использовать специальные методы для разреженных матриц или итерационные методы.

Можно также воспользоваться методами, реализованными для систем линейных уравнений.