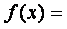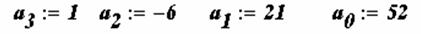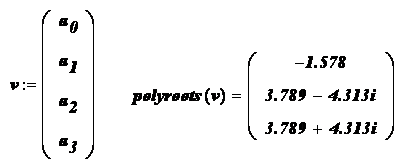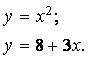Реферат: Отделение корней. Графический и аналитический методы отделения корней
| Название: Отделение корней. Графический и аналитический методы отделения корней Раздел: Рефераты по информатике Тип: реферат Добавлен 11:03:33 16 июня 2011 Похожие работы Просмотров: 2994 Комментариев: 22 Оценило: 8 человек Средний балл: 4.5 Оценка: 5 Скачать |
| Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
3. Аналитический метод (табличный или шаговый).
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет.
3.1. Отделение корней нелинейного уравнения
Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.
На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.
В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.
Аналитические методы основаны на функциональном анализе.
Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида
Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)
Верхняя граница положительных действительных корней 

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;
B – максимальный по модулю отрицательный коэффициент.
Нижнюю границу положительных действительных корней 

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то


Тогда все положительные корни многочлена лежат в интервале


Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.






Рассмотрим пример отделения корней с использованием этого аналитического метода.
Методом Лагранжа определим границы положительных и отрицательных корней многочлена.
3×8 – 5×7 – 6×3 – x – 9 = 0
K = 1 B = |– 9| an = 3


 |
k = 8 B = 3 an = 9
Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4



K = 1 B = 6 an = 9
 |
Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6
Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.
Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.
На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.
Графически корни можно отделить 2-мя способами:
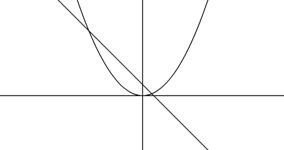
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.
Рис. 3.1 Отделение корней на графике f(x).
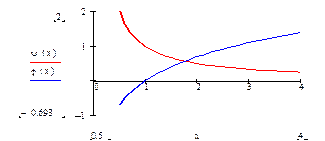
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.
На графике 2 корня.
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).
Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.
Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.
Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.
Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.
Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.
Недостаток метода – использование большого количества машинного времени.
Решение нелинейных уравнений и систем уравнений в пакете MathCAD
Решение нелинейных уравнений
Вычисление корней численными методами включает два основных этапа:
· уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.
Отделение корней нелинейного уравнения
Учитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.
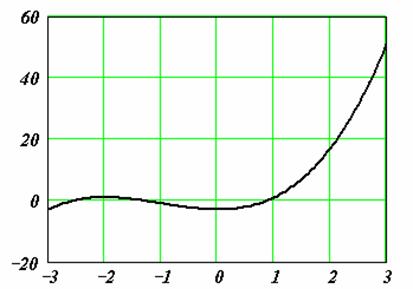
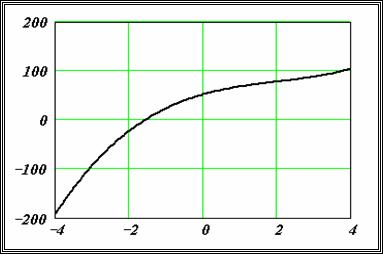
Пример. Дано алгебраическое уравнение
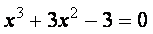
Определить интервалы локализации корней этого уравнения.
Пример. Дано алгебраическое уравнение
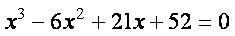
Определить интервалы локализации корней этого уравнения.
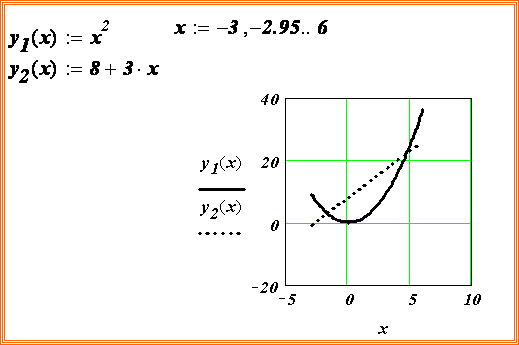
На рисунке приведен график функции 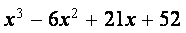
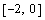
Уточнение корней нелинейного уравнения
Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.
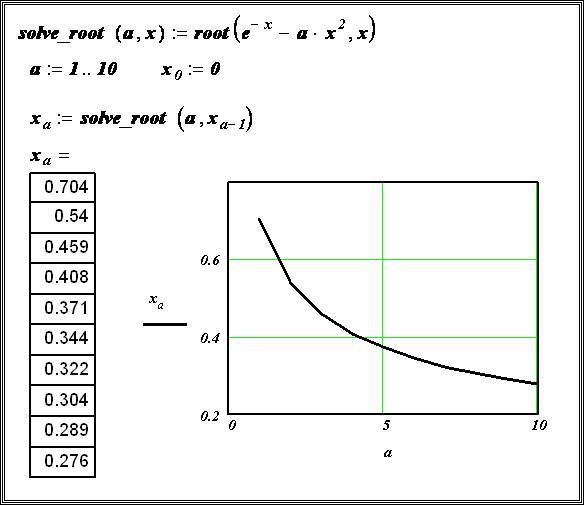
Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. 

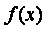
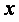
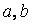
Пример. Используя функцию 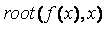
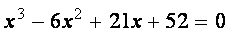
Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
Функция root с двумя аргументами требует задания (до обращения к функции) переменной 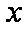
Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения 
Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка 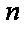
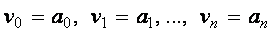
Пример. Используя функцию polyroots , найти все три корня уравнения 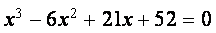
Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логический .
Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.
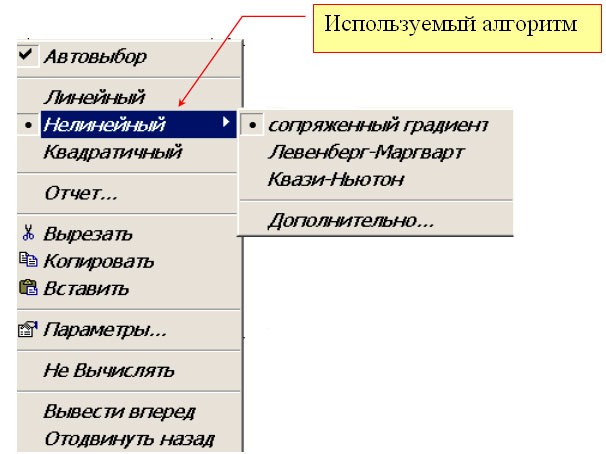
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.
Аналогично можно задать алгоритм решения и для функции Minerr ( x ).
Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.
Пример. Используя блок Given , вычислите корень уравнения 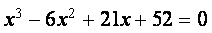
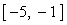
Решение систем уравнений
В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
В матричном виде систему можно записать как
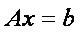
где 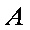
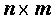
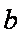

Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, 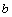
Решение систем нелинейных уравнений
MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.
Для решения системы уравнений необходимо выполнить следующие этапы.
Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.
Пример. Дана система уравнений:
Определить начальные приближения для решений этой системы.
Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨
Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .
Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке . Число аргументов функции должно быть равно числу неизвестных.
Следующие выражения недопустимы внутри блока решения:
· ограничения со знаком ¹ ;
· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;
· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).
Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.
Пример. Используя функцию 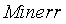
http://matica.org.ua/metodichki-i-knigi-po-matematike/vychislitelnaia-matematika/3-1-otdelenie-kornei-nelineinogo-uravneniia
http://pers.narod.ru/study/mathcad/07.html
 Министерство образования и науки РФ
Министерство образования и науки РФ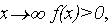 при
при 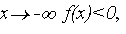 что уже свидетельствует о наличии хотя бы одного корня.
что уже свидетельствует о наличии хотя бы одного корня.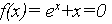 видим, что
видим, что 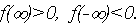 Обнаружив, что
Обнаружив, что 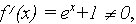 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).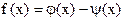 и строить графики функций
и строить графики функций 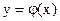 и
и 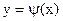 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.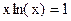 .
.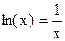 , т.е.
, т.е. 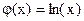 и
и 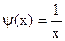 .
.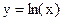 и
и 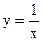 .
.