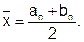Метод отделения корней при решении нелинейных уравнений

3.1. Отделение корней нелинейного уравнения

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.

На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.

В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)

Верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

, (3.3)

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения

(3.4)

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то

= (3.5)

Тогда все положительные корни многочлена лежат в интервале

≤x+≤.

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

и .

≤x–≤ = =.

Рассмотрим пример отделения корней с использованием этого аналитического метода.

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3×8 – 5×7 – 6×3 – x – 9 = 0

K = 1 B = |– 9| an = 3

= 4

9×8 + x7 + 6×5 + 5x – 3 = 0

k = 8 B = 3 an = 9

Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4

3×8 + 5×7 + 6×3 + x – 9 = 0

=

9×8 – x7 – 6×5 – 5x – 3 = 0

K = 1 B = 6 an = 9

Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

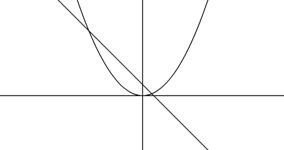
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.

Рис. 3.1 Отделение корней на графике f(x).

2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

На графике 2 корня.

Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

Отделение корней В Excel

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Лабораторная работа

Отделение корней нелинейного уравнения

Пусть имеется нелинейное уравнение .

Требуется найти корни этого уравнения. Численный процесс приближенного решения поставленной задачи разделяют два этапа: отделение корня и уточнение корня.

Для отделения корня необходимо определить промежуток аргумента , где содержится один и только один корень уравнения. Одна из точек этого промежутка принимается за начальное приближение корня. В зависимости от метода, который предполагается использовать для уточнения корня, требуется определение некоторых свойств отделенного корня и поведения функции на отрезке отделения. Например, при использовании метода деления пополам, необходимо и достаточно установить лишь непрерывность функции на отрезке отделения.

Этап отделения корня уравнения алгоритмизирован только для некоторых классов уравнений (наиболее известным из которых является класс алгебраических уравнений), поэтому отделение корней нелинейных уравнений, обычно, выполняется «вручную» с использованием всей возможной информации о функции . Часто применяется графический метод отделения действительных корней, обладающий большой наглядностью.

Методы отделения корней

Отделение корней во многих случая можно произвести графически. Учитывая, что действительные корни уравнения F ( x )=0 – это есть точки пересечения графика функции y = F ( x ) с осью абсцисс y =0, нужно построить график функции y = F ( x ) и на оси OX отметить отрезки, содержащие по одному корню. Но часто для упрощения построения графика функции y = F ( x ) исходное уравнение заменяют равносильным ему уравнением f ₁ ( x )= f ₂ ( x ). Далее строятся графики функций y ₁ = f ₁ ( x ) и y ₂ = f ₂ ( x ), а затем по оси OX отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков.

На практике данный способ реализуется следующим образом: например, требуется отделить корни уравнения cos(2 x )+ x -5=0 графически на отрезке [–10;10], используя Excel .

Построим график функции f (x)=cos(2 x )+x-5 в декартовой системе координат. Для этого нужно:

Ввести в ячейку A1 текст х .

Ввести в ячейку B1 текст y =cos(2 x )+ x -5.

Ввести в ячейку А2 число -10, а в ячейку А3 число -9.

Выделить ячейки А2 и А3.

Навести указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы рамка охватила диапазон ячеек А2:А22.

Ячейки автоматически заполняются цифрами :

Ввести в ячейку В2 формулу =COS(2*A2)+A2-5.

Методом протягивания заполнить диапазон ячеек В3:В22.

Вызвать «Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать «далее».

Указать диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон данных В2:В22.

Выбрать вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.

В поле «подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».

Подписать названия осей x и y соответственно, нажать «далее».

Вывести диаграмму на том же листе, что и таблица, нажать кнопку «готово».

В итоге получаем следующее (рисунок 1):

Рисунок 1 – Локализация корня

Анализируя полученное изображение графика, можно сказать, что уравнение cos(2 x )+ x -5=0 имеет один корень – это видно из пересечения графика функции y=cos(2 x )+ x -5 с осью OX. Можно выбрать отрезок, содержащий данный корень: [5;6] – отрезок локализации .

Для подтверждения полученных данных, можно решить эту же задачу вторым способом. Для этого необходимо уравнение cos(2 x )+ x -5=0 преобразовать к виду: cos(2 x )=5- x . Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y ₁ =cos(2 x ) и y ₂ =5- x . Для решения этой задачи в Excel необходимо выполнить следующие действия:

Вести в ячейки А1:C1 соответственно текст: « x », « y ₁ =cos(2 _x )», « y ₂ =5- x ».

A2:A22 заполнить так же как при решении задачи первым способом.

В В2 ввести формулу =COS(2*A2).

Методом протягивания заполнить диапазон ячеек В3:В22.

В С2 ввести =5-A2.

Методом протягивания заполнить диапазон ячеек С3:С22.

С помощью Мастера диаграмм выбрать график (первый вид).

В данном случае диапазон данных следует указывать для построения двух графиков. Для этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.

Перейти на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.

Подписать ось x , выбрав диапазон А2:А22.

Подписать соответственно оси x и y .

Поместить диаграмму на имеющемся листе.

Результат представлен на рисунке 2: Анализируя полученный результат, можно сказать, что точка пересечения двух графиков попадает на тот же самый отрезок локализации [5;6] , что и при решении задачи первым способом.

Рисунок 2 – Локализация корня

Аналитический способ отделения корней

Аналитический способ отделения корней основан на следующей теореме , известной из курса математического анализа.

ТЕОРЕМА: Если непрерывная на функция , определяющая уравнение , на концах отрезка принимает значения разных знаков, т.е. , то на этом отрезке содержится, по крайней мере, один корень уравнения. Если же функция непрерывна и дифференцируема и ее производная сохраняет знак внутри отрезка , то на этом отрезке находится только один корень уравнения.

В случае, когда на концах интервала функция имеет одинаковые знаки, на этом интервале корни либо отсутствуют, либо их четное число.

Для отделения корней аналитическим способом выбирается отрезок , на котором находятся все интересующие вычислителя корни уравнения. Причем на отрезке функция F (x) определена, непрерывна и F ( a )* F ( b ) . Требуется указать все частичные отрезки , содержащие по одному корню.

Б
удем вычислять значение функции F ( x ) , начиная с точки x = a , двигаясь вправо с некоторым шагом h . Если F ( x )* F (x+ h ) , то на отрезке [ x ; x + h ] существует корень (рисунок 3).

Рисунок 3 – Аналитический способ локализации корней

Доказательство существования и единственности корня на отрезке.

В качестве примера рассмотрим функцию f (x)=cos(2 x )+x-5 .

Ввести в ячейки А1, В1 и С1 соответственно « x », « y =cos(2 x )+ x -5» и «ответ».

В А2 и А3 ввести граничные значения отрезка изоляции.

В В2 ввести формулу =COS(2*A2)+A2-5 и методом протягивания заполнить В3.

В С2 ввести формулу =ЕСЛИ(B2*B3

Таким образом, на отрезке изоляции корень существует:

Р
исунок 4 – Проверка существования корня на отрезке

Для доказательства единственности корня на отрезке изоляции необходимо выполнить следующие действия:

Продолжить работу в том же документе MS Excel.

Заполнить D1 и E1 соответственно: « y’ =-sin(2 x )*2+1» и «ответ» (причем выражение y’ =-sin(2 x )*2+1 – это производная первого порядка от функции y =cos(2 x )+ x -5).

Ввести в D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.

Ввести в E2 =ЕСЛИ(D2*D3>0;»корень на данном отрезке единственный»;»Корень не единственный»).

В
результате получаем (рисунок 5):

Рисунок 5 – Доказательство единственности корня на отрезке

Таким образом доказано существование и единственность корня на отрезке изоляции.

Рассмотрим решение задачи отделения корней уравнения
cos(2 x )+ x -5=0 аналитическим способом с шагом 1 на отрезке [-10;10].

Чтобы отделить корни уравнения аналитическим способом с помощью Excel, необходимо выполнить следующее:

Заполнить ячейки A1:D1 соответственно: « x », « y =cos(2 x )+ x -5», « h », «ответ».

В С2 ввести значение 1.

Ввести в А2 значение -10.

Ввести в А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.

В В2 ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.

В
С3 ввести формулу =ЕСЛИ(B2*B3

В результате получаем следующее (рисунок 6):

Рисунок 6 – Отделение корня

Следующий пример (рисунок 7) демонстрирует отделение нескольких корней. Пусть исследуется функция cos ( x )=0,1 x на интервале [–10;10] с шагом 1.

Табулирование функции и построение графика осуществляется как в предыдущих примерах. Видно, что на заданном отрезке имеем 7 корней, находящихся внутри отрезков: [-10;-9]; [-9;-8]; [-5;-4]; [-2;-1]; [1;2]; [5;6]; [7;8].

Рисунок 7 – Отделение корней

Обратим внимание на то, что надежность рассмотренного алгоритма отделения корней уравнения зависит как от характера функции F (x), так и от выбранной величины шага h . Для повышения надежности следует выбирать при отделении корней достаточно малые значения h .

1. Выполнить отделение корней следующих функций:

Тема 1.2. Методы решения нелинейных уравнений

Тема 1.2. Методы решения нелинейных уравнений

Постановка задачи

Отделение корней

1.2.2.1. Графическое отделение корней

1.2.2.2. Аналитическое отделение корней

Уточнение корней

1.2.3.1. Метод половинного деления

1.2.3.2. Метод итерации

1.2.3.3. Метод Ньютона (метод касательных)

1.2.3.4. Метод хорд

1.2.3.5. Сравнение методов решения нелинейных уравнений

1.2.4. Тестовые задания по теме «Методы решения нелинейных уравнений»

Постановка задачи

Одной из важнейших и наиболее распространенных задач математического анализа является задача определения корней уравнения с одним неизвестным, которое в общем виде можно представить как f(x) = 0. В зависимости от вида функции f(x)различают алгебраические и трансцендентные уравнения. Алгебраическими уравненияминазываются уравнения, в которых значение функции f(x)представляет собой полином n-й степени:

f(x) = Р(х) = a_n x n + a₂ x 2 + …+ a₁ x + a₀ = 0.(1.2.1-1)

Всякое неалгебраическое уравнение называется трансцендентным уравнением. Функция f(x) в таких уравнениях представляет собой хотя бы одну из следующих функций: показательную, логарифмическую, тригонометрическую или обратную тригонометрическую.

Решением уравнения f(x)=0называется совокупность корней, то есть такие значения независимой переменной 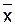, при которых уравнение обращается в тождество . Однако, точные значения корней могут быть найдены аналитически только для некоторых типов уравнений. В частности, формулы, выражающие решение алгебраического уравнения, могут быть получены лишь для уравнений не выше четвертой степени. Еще меньше возможностей при получении точного решения трансцендентных уравнений. Следует отметить, что задача нахождения точных значений корней не всегда корректна. Так, если коэффициенты уравнения являются приближенными числами, точность вычисленных значений корней заведомо не может превышать точности исходных данных. Эти обстоятельства заставляют рассматривать возможность отыскания корней уравнения с ограниченной точностью (приближенных корней).

Задача нахождения корня уравнения с заданной точностью ( >0)считается решенной, если вычислено приближенное значение , которое отличается от точного значения корня не более чем на значение e

(1.2.1-2)

Процесс нахождения приближенного корня уравнения состоит из двух этапов:

1) отделение корней (локализация корней);

Итерационное уточнение корней.

На этапе отделения корней решается задача отыскания возможно более узких отрезков 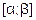, в которых содержится один и только один корень уравнения.

Этап уточнения корня имеет своей целью вычисление приближенного значения корня с заданной точностью. При этом применяются итерационные методы вычисления последовательных приближений к корню: x₀, x₁, . x_n, …, в которых каждое последующее приближение x_n+1вычисляется на основании предыдущего x_n. Каждый шаг называется итерацией. Если последовательность x₀, x₁, . x_n, …при n ® ¥ имеет предел, равный значению корня , то говорят, что итерационный процесс сходится.

Существуют различные способы отделения и уточнения корней, которые мы рассмотрим ниже.

Отделение корней

Корень уравнения f(x)=0считается отделенным (локализованным) на отрезке , если на этом отрезке данное уравнение не имеет других корней. Чтобы отделить корни уравнения, необходимо разбить область допустимых значений функции f(x) на достаточно узкие отрезки, в каждом их которых содержится только один корень. Существуют графический и аналитический способы отделения корней.

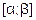
Уточнение корней

Задача уточнения корня уравнения с точностью , отделенного на отрезке [a;b], состоит в нахождении такого приближенного значения корня , для которого справедливо неравенство .Если уравнение имеет не один, а несколько корней, то этап уточнения проводится для каждого отделенного корня.

Метод половинного деления

Пусть корень уравнения f(x)=0 отделен на отрезке [a;b], то есть на этом отрезке имеется единственный корень, а функция на данном отрезке непрерывна.

Метод половинного деления позволяет получить последовательность вложенных друг в друга отрезков [a_1;b₁], [a₂;b₂], …,[a_i;b_i],…, [a_n;b_n], таких что f(a_i).f(b_i)

может быть принято за приближенное значение корня, например его середину отрезка

В методе половинного деления от итерации к итерации происходит последовательное уменьшение длины первоначального отрезка [a₀;b₀]в два раза (рис. 1.2.3-1). Поэтому на n-м шаге справедлива следующая оценка погрешности результата:

(1.2.3-1)

где — точное значение корня, х_nÎ [a_n;b_n] – приближенное значение корня на n-м шаге.

Сравнивая полученную оценку погрешности с заданной точностью , можно оценить требуемое число шагов:

(1.2.3-2)

Из формулы видно, что уменьшение величины e (повышение точности) приводит к значительному увеличению объема вычислений, поэтому на практике метод половинного деления применяют для сравнительно грубого нахождения корня, а его дальнейшее уточнение производят с помощью других, более эффективных методов.

Рис. 1.2.3-2. Схема алгоритма метода половинного деления

Схема алгоритма метода половинного деления приведена на рис. 1.2.3-2. В приведенном алгоритме предполагается, что левая часть уравнения f(x)оформляется в виде программного модуля.

Пример 1.2.3-1. Уточнить корень уравнения x 3 +x-1=0 с точностью =0.1, который локализован на отрезке [0;1].

Результаты удобно представить с помощью таблицы 1.2.3-3.

После четвертой итерации длина отрезка |b₄-a₄| = |0.688-0.625| = 0.063 стала меньше величины e, следовательно, за приближенное значение корня можно принять значение середины данного отрезка: x = (a₄+b₄)/2 = 0.656.

Значение функции f(x) в точке x = 0.656 равно f(0.656) = -0.062.

Метод итерации

Метод итераций предполагает замену уравнения f(x)=0 равносильным уравнением x=j(x). Если корень уравнения отделен на отрезке [a;b], то исходя из начального приближения x₀Î[a;b], можно получить последовательность приближений к корню

x₁ = j(x₀), x₂ = j(x₁), …, , (1.2.3-3)

где функция j(x) называется итерирующей функцией.

Условие сходимости метода простой итерации определяется следующей теоремой.

Пусть корень х* уравнения x=j(x) отделен на отрезке [a;b]и построена последовательность приближений по правилу x_n=j(x_n-1). Тогда, если все члены последовательности x_n=j(x_n-1) Î [a;b] и существует такое q (0 -1. Таким образом, очевидно, что если |j’(x)| 1. На рис. 1.2.3-4а показан случай, когда j’(x)>1, а на рис. 1.2.3-4b – когда j’(x) 0.

Таким образом, если за неподвижную точку приняли точку а,то в качестве начального приближения выступает х₀ = b, и наоборот.

Достаточные условия, которые обеспечивают вычисление корня уравнения f(x)=0 по формуле хорд, будут теми же, что и для метода касательных (метод Ньютона), только вместо начального приближения выбирается неподвижная точка. Метод хорд является модификацией метода Ньютона. Разница состоит в том, что в качестве очередного приближения в методе Ньютона выступает точка пересечения касательной с осью 0Х, а в методе хорд – точка пересечения хорды с осью 0Х – приближения сходятся к корню с разных сторон.

Оценка погрешности метода хорд определяется выражением

(1.2.3-15)

Условие окончания процесса итераций по методу хорд

(1.2.3-16)

В случае, если M₁ x – 3x = 0, отделенный на отрезке [0;1] с точностью 10 -4 .

Проверим условие сходимости:

Следовательно, за неподвижную точку следует выбрать а=0, а в качестве начального приближения принять х₀=1, поскольку f(0)=1>0 и f(0)*f»(0)>0.

Результаты расчета, полученные с использованием формулы
1.2.3-14, представлены в таблице 1.2.3-4.

Требуемая точность достигается на 8-й итерации. Следовательно, за приближенное значение корня можно принять х = 0.6191.

Схема алгоритма метода хорд приведена на рис. 1.2.3-10.

Выбор неподвижной точки, определяющей вид расчетной формулы, производится путем сравнения одного из концов отрезка [a;b] с начальным приближением (x₀=a). В качестве неподвижного конца отрезка (точка с) выбирается тот, который не совпадает с начальным приближением.

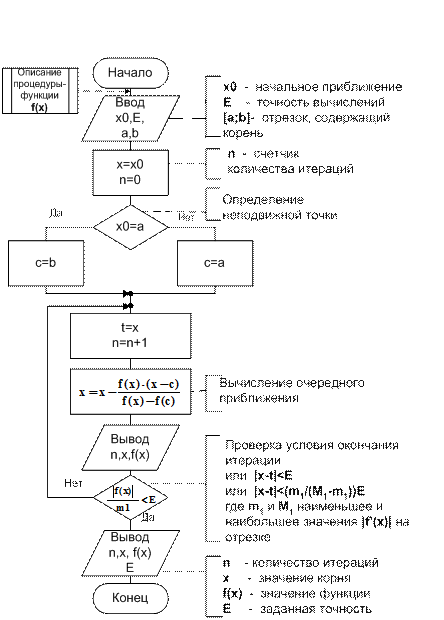Рис. 1.2.3-10. Схема алгоритма метода хорд

Нелинейное уравнение – это

1)алгебраическое или трансцендентное уравнение

2)алгебраическое уравнение

3)тригонометрическое уравнение

4)трансцендентное уравнение

Тема 1.2. Методы решения нелинейных уравнений

Постановка задачи

Отделение корней

1.2.2.1. Графическое отделение корней

1.2.2.2. Аналитическое отделение корней

Уточнение корней

1.2.3.1. Метод половинного деления

1.2.3.2. Метод итерации

1.2.3.3. Метод Ньютона (метод касательных)

1.2.3.4. Метод хорд

1.2.3.5. Сравнение методов решения нелинейных уравнений

1.2.4. Тестовые задания по теме «Методы решения нелинейных уравнений»

Постановка задачи

Одной из важнейших и наиболее распространенных задач математического анализа является задача определения корней уравнения с одним неизвестным, которое в общем виде можно представить как f(x) = 0. В зависимости от вида функции f(x)различают алгебраические и трансцендентные уравнения. Алгебраическими уравненияминазываются уравнения, в которых значение функции f(x)представляет собой полином n-й степени:

f(x) = Р(х) = a_n x n + a₂ x 2 + …+ a₁ x + a₀ = 0.(1.2.1-1)

Всякое неалгебраическое уравнение называется трансцендентным уравнением. Функция f(x) в таких уравнениях представляет собой хотя бы одну из следующих функций: показательную, логарифмическую, тригонометрическую или обратную тригонометрическую.

Решением уравнения f(x)=0называется совокупность корней, то есть такие значения независимой переменной 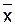, при которых уравнение обращается в тождество . Однако, точные значения корней могут быть найдены аналитически только для некоторых типов уравнений. В частности, формулы, выражающие решение алгебраического уравнения, могут быть получены лишь для уравнений не выше четвертой степени. Еще меньше возможностей при получении точного решения трансцендентных уравнений. Следует отметить, что задача нахождения точных значений корней не всегда корректна. Так, если коэффициенты уравнения являются приближенными числами, точность вычисленных значений корней заведомо не может превышать точности исходных данных. Эти обстоятельства заставляют рассматривать возможность отыскания корней уравнения с ограниченной точностью (приближенных корней).

Задача нахождения корня уравнения с заданной точностью ( >0)считается решенной, если вычислено приближенное значение , которое отличается от точного значения корня не более чем на значение e

(1.2.1-2)

Процесс нахождения приближенного корня уравнения состоит из двух этапов:

1) отделение корней (локализация корней);