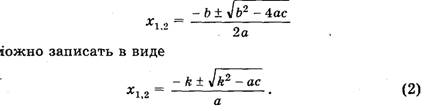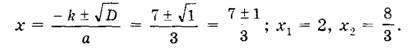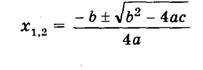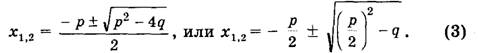«Решение квадратных уравнений способом «переброски»
план-конспект занятия по алгебре (8 класс) на тему
Ознакомление с одним из способов решения квадратных уравнений, который можно назвать способом «переброски».
Скачать:
| Вложение | Размер |
|---|---|
| sposob_perebroski.doc | 93 КБ |
Предварительный просмотр:
Материал к занятию по теме «Решение квадратных уравнений способом «переброски»
Тема: «Решение квадратных уравнений способом «переброски»
Тип занятия: Изучение нового материала и первичное закрепление с комплексным применением знаний и способов деятельности
Вид занятия: Урок углубления знаний
Возраст учащихся: 8 класс
Форма работы: индивидуальная, групповая
Оборудование: мультимедийный компьютер
- Познавательный
- Систематизирующий
- Коммуникативный
- Логический
Формирование знания решения квадратных уравнений с помощью способа «переброски»
- Познакомить с теорией способа решения квадратных уравнений с помощью способа «переброски»
- Познакомить с применением способа решения квадратных уравнений с помощью способа «переброски»
- Сформировать умения составлять алгоритмы для данного способа решения квадратных уравнений
- Развитие вычислительных навыков
- Развитие кругозора учащихся
- Развитие умения наблюдать, анализировать
- Способствовать интеллектуальному развитию учащихся, формированию качеств мышления, познавательных интересов, творческих способностей учащихся
- Познакомить учащихся с интересными фактами из истории
- Развитие коммуникативных качеств личности
- Воспитание навыков сотрудничества в процессе совместной работы.
- Содействовать воспитанию интереса к математике, активности, мобильности, отношения ответственной зависимости, взаимопомощи, умения общаться, толерантности у детей
- Воспитание самостоятельности, умения представлять выбранный способ решения уравнения
- Организационный момент. Вступительное слово учителя
- Актуализация опорных теоретических и практических знаний о квадратных уравнениях
- Объяснение нового материала
- Закрепление нового материала
- Подведение итогов
Оформление доски: на доске написано
«Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением. Извне он может получить только возбуждение». А Дистервег
Вступительное слово учителя. Сообщается цель, задачи занятия, план работы на занятии.
Актуализация опорных теоретических и практических знаний.
Коллективная работа. Устно.
Прежде всего, вспомним, какие уравнения называются квадратными. /Уравнение вида , где х — переменная, a,b,c – числа , называется квадратным./ Квадратное уравнение, записанное в таком виде, является стандартным видом уравнения. Как называются числа a, b, c ?
/ а – старший коэффициент, b – второй коэффициент, с – свободный член/
Вспомним, как традиционно решаются квадратные уравнения разных видов. Первый вид квадратных уравнений – неполные квадратные уравнения. С этим видом квадратных уравнений мы познакомились на первых уроках изучения квадратных уравнений. Вспомним, какие виды неполных квадратных уравнений бывают и как они решаются.
Вспомним, как традиционно решаются квадратные уравнения, записанные в стандартном виде. Прежде всего, обратимся к понятию дискриминанта. Для чего и зачем он нужен? Вспомните слово “дискриминация”, что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к разным людям. Оба слова (и дискриминант, и дискриминация) происходят от одного латинского слова, означающего “различающий”. Дискриминант различает квадратные уравнения по числу корней (анализ слайда). Важное дополнение: в таких случаях ( D ) обычно уточняют – нет действительных корней. Дело в том, что в математике, кроме действительных чисел, рассматриваются так называемые мнимые числа; так вот, мнимые корни у такого уравнения есть. О мнимых числах и разрешимости таких квадратных уравнений мы поговорим в старших классах. Мы вспомнили всю “азбуку” квадратного уравнения?
/Нет. Мы не вспомнили теорему Виета./
Решение задач на применение теоремы Виета и теоремы, обратной теореме Виета.
а) В уравнениях найти подбором корни уравнения:
х 2 – 6х + 8 = 0
(Д = 1; х 1 = 2, х 2 = 4)
z 2 + 5z + 6 = 0
(Д = 1; z 1 = – 3, z 2 = –2)
б) Составить квадратное уравнение, корнями которого являются числа:
3; 4
(х 2 – 7х + 12 = 0)
–2; 5
(х 2 – 3х – 10 = 0)
в) Один из корней уравнения равен 3. Найти второй корень уравнения.
х 2 – 21х + 54 = 0
3 и ?
(х 2 = 18)
х 2 + 17х – 60 = 0
3 и ?
(х 2 = – 20)
Подведем итог этого этапа:
- Что утверждает теорема Виета?
- Сформулируйте теорему, обратную теореме Виета.
- Чему равна сумма и произведение корней квадратного уравнения ах 2 + + вх + с = 0 ?
Это интересно. Биографическая миниатюра. Ф. Виет. (Сообщение учащегося).
Формулы решения квадратных уравнений в Европе были впервые написаны в 1202 году. Вывод формулы решения квадратного уравнения встречается у французского математика Ф. Виета. Франсуа Виет родился в провинции Франции в 1540 году. Виет имел возможность получить хорошее образование и относился к обучению очень серьезно. Став юристом, он продолжал заниматься математикой, астрономией и космологией. В 1591 году Виет ввел буквенные обозначения не только для неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало впервые возможным выражение свойств уравнений и их корней формулами. Среди открытий сам Виет особенно высоко ценил установление зависимости между корнями и коэффициентами уравнений.
По праву достойна в стихах быть воспета.
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого,
Умножишь ты корни – и дробь уж готова.
В числителе С, в знаменателе А.
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда?
В числителе В, в знаменателе А.
А все могло быть по-другому. Эта замечательная теорема могла быть открыта совсем другим талантливым человеком. А знаете почему?
Испанские инквизиторы изобрели очень сложную тайнопись (шифр), которая все время изменялась и дополнялась. Благодаря этому шифру воинствующая и сильная в то время Испания могла свободно переписываться с противниками французского короля даже внутри Франции, и эта переписка оставалась неразгаданной. После бесплодных попыток найти ключ к шифру король обратился к Виету. Известно, что Виет, две недели подряд дни и ночи просидев за работой, все же нашел ключ к испанскому шифру. После этого неожиданно для испанцев Франция стала выигрывать одно сражение за другим. Испанцы долго недоумевали. Наконец им стало известно, что шифр для французов уже не секрет и что виновник его расшифровки – Виет. Будучи уверенными, в невозможности разгадать способ тайнописи людьми, они обвинили Францию перед Папой Римским и инквизицией в кознях дьявола, а Виета обвинили, что он был в союзе с дьяволом и приговорили его к сожжению на костре. К счастью для науки, он не был выдан инквизиции.
Решение квадратных уравнения, используя свойства коэффициентов. (Повторение предыдущей темы факультативных занятий)
- 345х 2 – 137х – 208 = 0
- 313х 2 + 326х + 13 = 0
Задание учащиеся выполняют самостоятельно. Взаимоконтроль.
а + b + с = 345 – 137 – 208 = 0 , значит, х = 1 , х = – 208/345
а – b + с = 313 – 326 + 13 = 0 , значит, х = – 1 , х = – 13/313
Изучение нового материала. Ознакомление ещё с одним способом решения квадратных уравнений, который можно назвать так: способ «переброски».
Рассмотрим квадратное уравнение
ах 2 + bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + а bх + ас = 0.
Пусть ах = у , откуда х = ; тогда приходим к уравнению
равносильного данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета. Окончательно получаем х 1 = и х 1 = . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
- Пример 1 (объясняет учитель)
Решим уравнение 2х 2 – 11х + 15 = 0 .
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 – 11y + 30 = 0 .
Согласно теореме Виета
- Пример 2 (один ученик решает на доске, остальные в тетрадях)
у 1 = 6 х 1 = 6/2 х 1 = 3
у 2 = 3 ↔ х 2 = 3/2 ↔ х 2 = 1,5
«Математическая эстафета». Работа по командам. На последней парте каждого ряда находится листок с 6 заданиями (по 2 задания на каждую парту). Ученики, получившие листок, выполняют первые 2 задания (разрешается совместная работа) и передают листок впереди сидящим ребятам.
Решите уравнения, используя метод «переброски»:
- 10х 2 – 11х + 3 = 0 3. 3х 2 + 11х + 6 = 0 5. 6х 2 + 5х – 6 = 0
- 2х 2 + х – 10 = 0 4. 5х 2 – 11х + 6 = 0 6. 4х 2 + 12х + 5 = 0
Работа считается оконченной, когда учитель получает три листка (по количеству рядов) с выполненными 6 заданиями.
Побеждают учащиеся того ряда, в котором раньше решат шесть примеров.
Проверка итогов работы осуществляется с помощью мультимедийного компьютера.
Оценка – 6 баллов (по 1 баллу за каждый верно выполненный пример).
1. Самооценка труда учащихся:
- В каких знаниях уверен;
- Выполнил ли программу занятия полностью;
- Какие виды работ вызвали затруднения и требуют повторения;
- Помогло ли занятие продвинуться в знаниях, умениях, навыках по предмету.
2. Оценка труда товарищей:
- Насколько результативным было занятие сегодня;
- Кто, по вашему мнению, внёс наибольший вклад в его результаты;
- Кому, над чем следовало бы ещё поработать.
3. Оценка результатов занятия учителем:
- Оценка работы группы (активность, адекватность ответов, неординарность работы отдельных детей, уровень самоорганизации, прилежание).
4. Выводы по занятию.
Решить уравнения. Каждое решить 3 различными способами.
- 3х 2 + 5х – 2 = 0
- х 2 – 8х + 7 = 0
- 5х 2 – 11 х + 2 = 0
Разработка урока по теме «Квадратные уравнения (методы решения)»
Разделы: Математика
Цели урока:
обучающие
- обобщение и систематизация знаний по теме.
- ликвидация пробелов в знаниях учащихся.
- установление внутри предметных связей изученной темы с другими темами курса алгебры.
развивающие
- расширение кругозора учащихся
- пополнение словарного запаса
- развитие мышления, внимания, умения учиться
воспитание общей культуры
Оборудование: PC, проектор, экран; у каждого ученика: конспект, пригласительный билет
Организационный момент.
— Приветствие учащихся; проверка готовности к уроку.
— Сообщение темы урока: “Квадратные уравнения. Методы решения”.
— Совместное формулирование цели урока
Сегодня у нас несколько необычный урок – урок-презентация методов решения квадратных уравнений. Как вы думаете, как можно сформулировать цель нашего урока исходя из его темы?
(Речь идет о методах, значит их много (больше одного), надо каждый вспомнить и проиллюстрировать примером)
Иными словами обобщить и систематизировать весь предшествующий опыт решения квадратных уравнений. А зачем нам это надо?
(Для возможности выбора рационального пути решения).
Итак, наша цель: обобщить опыт решения квадратных уравнений, научиться выбирать рациональный путь решения.
Актуализация знаний.
Прежде всего, вспомним, какие уравнения называются квадратными.
(Уравнение вида 

Квадратное уравнение, записанное в таком виде, является стандартным видом уравнения. Как называются числа a, b, c ?
(а – старший коэффициент, b – второй коэффициент, с – свободный член)
Вспомним, как традиционно решаются квадратные уравнения разных видов.
Первый вид квадратных уравнений – неполные квадратные уравнения.
С этим видом квадратных уравнений мы познакомились на первых уроках изучения квадратных уравнений. Вспомним, какие виды неполных квадратных уравнений бывают и как они решаются. (анализ таблицы)
(Подписывают и заполняют таблицу)
Проверим. Возьмите в руки простой карандаш и сверим ответы.
Поднимите руки те, кто безошибочно справились с работой. Молодцы! Передайте свои заполненные билеты вперед.
Презентация специальных методов.
Обратимся к конспекту урока. Помимо традиционных методов решения квадратных уравнений есть еще специальные и общие методы. Рассмотрим каждый из специальных методов в отдельности. И оценим его “перспективы”.
Метод выделения квадрата двучлена.
Цель: Привести уравнение общего вида к неполному квадратному уравнению.
В этом нам помогут формулы сокращенного умножения, а именно, квадратов суммы и разности:
Решим уравнение х 2 -6х+8=0 методом выделения квадрата двучлена.

Замечание: метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения.
(Обратить внимание на возможность пойти иным путем, применяя формулу разности квадратов).
Метод “переброски” старшего коэффициента
Суть метода состоит в то, что корни квадратных уравнений
ax 2 + bx + c = 0 и y 2 +by+ac=0

В некоторых случаях удобно решать сначала не данное уравнение ax 2 + bx + c = 0, а приведенное y 2 +by+ac=0, которое получается из данного “переброской” коэффициента а, а затем разделить найденные корни на а для нахождения корней исходного уравнения.
Пример: решите уравнение
заменим приведенным квадратным уравнением с “переброской” коэффициента а
( D>0 ), по теореме, обратной теореме Виета, подбором найдем корни
вернемся к корням исходного уравнения
Замечание: метод хорош для квадратных уравнений с “удобными” коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.
Следующие два метода также применимы при определенных условиях и позволяют избежать громоздких вычислений.
Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй по теореме Виета равен
Пример: решите уравнение
a = 157, b = 20, c = -177
a + b+ c =157+20-177=0
x2 = 
Ответ: 1;
Если в квадратном уравнении a+c=b, то один из корней равен -1, а второй по теореме Виета равен
Пример: решите уравнение
a = 203, b = 220, c = 17
a + c = 203 + 17 = 220 = b
Ответ: -1;
Вывод: при решении квадратного уравнения стандартного вида полезно сначала проверить являются ли числа 1 и -1 корнями уравнения.
Однако, при выборе пути решения квадратного уравнения следует помнить, что помимо специальных методов возможно применение и общих методов решения уравнений.
К таким методам относятся:
- Разложение на множители;
- Введение новой переменной;
- Графический способ.
Презентация общих методов решения уравнений (Презентация).
Метод разложения на множители.
Цель: Привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х) – многочлены относительно х.
Способы:
- Вынесение общего множителя за скобки;
- Использование формул сокращенного умножения;
- Способ группировки.
Пример: решите уравнение
произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а второй при этом не теряет смысла, или когда оба равны нулю.
Ответ: -1; 
Метод введения новой переменной
Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной.
Пример: решите уравнение
Произведем замену переменной
(Устно проверим условие D > 0) по теореме, обратной теореме Виета
Произведем обратную замену и вернемся к переменной х
Вывод: при решении уравнения не следует торопиться выполнять преобразования. Посмотрите, нельзя ли записать уравнение проще, введя новую переменную.
И, наконец, наиболее “зрелищный” метод.
Графический метод.
Для решения уравнения f(x) = g(x) необходимо построить графики функций y = f(x),
y = g(x) и найти точки их пересечения; абсциссы точек пересечения и будут корнями уравнения.

(Устно обсудить области определения )
Построим график функции
Графиком является парабола, “ветви” которой направлены вверх (0;0) – вершина параболы график симметричен относительно оси ординат
| X | 1 | 2 | 3 |
| Y | 1 | 4 | 9 |
Построим график функции y = x + 2
Линейная функция. Графиком является прямая.
| X | 0 | -2 |
| Y | 2 | 0 |
Точки пересечения: А(-1;1) и В(2;4)
Применяя графический метод в данном случае мы нашли точное значение корней, но так бывает не всегда. Однако, графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.
Историческая справка
Посмотрите на многообразие методов решения. Как, когда, сразу ли появилось такое многообразие? Как много вопросов…
Безусловно, человечество “додумалось” до всего не сразу и в одночасье. Для этого потребовались долгие годы и даже столетия.
Обратимся к историческому путеводителю.
Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными относятся во второму тысячелетию до н.э. Это эпоха расцвета Вавилонии и Древнего Египта.
Первое тысячелетие н.э. – Римские завоевательные войны. К этому периоду относится творчество Диофанта. Его трактат “Арифметика” содержит ряд задач, решаемых при помощи квадратных уравнений. В IX веке узбекский математик Аль-Хорезми в Трактате “Алгебра” классифицирует квадратные уравнения. Для нас это время знаковое тем, что приблизительно в это время образуется древнерусское государство Киевская Русь.
Все это время отличные по записи уравнения считались различными. Не было единого подхода к их решению.
И только в XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым заложил основы буквенной алгебры.
Более подробно с этапами развития методов решения квадратных уравнений, а так же личностью Виета и его вклада в развитие алгебры мы сможем познакомиться на конференции.
Подведение итогов.
Итак, подведем итог.
Решение квадратных уравнений, возможно, осуществлять разными методами. Для квадратных уравнений применимы не только традиционные и специальные методы решения, но и общие методы решения уравнений.
Сегодня мы обобщили опыт решения квадратных уравнений и посмотрим, как научились выбирать наиболее рациональный метод решения.
Попробуйте расшифровать высказывание из копилки “Золотых мыслей”.
Для этого проанализируйте представленные уравнения, выберите для каждого более рациональный метод решения и укажите номер этого метода. Затем согласно ключу расставьте в нижней таблице слоги и прочтите высказывание.
Итак, получили высказывание Ян Амос Коменского: “Учиться нелегко, но интересно”.
Я думаю, эти слова как нельзя, кстати, подходят для окончания нашей сегодняшней презентации.
Домашнее задание
- Решите уравнение х 2 +6х-16=0 по формуле, выделением квадрата двучлена и графическим методом
- Составьте уравнения на применение теорем (метод 9, 10).
- Решите уравнение 3х 2 +5х+2=0 пятью способами.
- Решите уравнение (х 2 -х) 2 -14(х 2 -х)+24=0 методом введения новой переменной.
СПОСОБ: Решение уравнений способом «переброски»
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах 2 + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
равносильно данному. Его корни у1и у2 найдем с помощью теоремы Виета.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 2х 2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 – 11у + 30 = 0.
Согласно теореме Виета
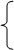
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение
ах 2 + bх + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x 2 + b/a • x + c/a = 0.
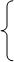
По условию а – b + с = 0, откуда b = а + с. Таким образом,
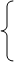
т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.
1) Решим уравнение 345х 2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
2)Решим уравнение 132х 2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
Б. Если второй коэффициент b = 2k – четное число, то формулу корней
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k 2 – ac = (- 7) 2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;
В. Приведенное уравнение
совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
Формулу (3) особенно удобно использовать, когда р — четное число.
Пример. Решим уравнение х 2 – 14х – 15 = 0.
7. СПОСОБ: Графическое решение квадратного уравнения.
Если в уравнении
перенести второй и третий члены в правую часть, то получим
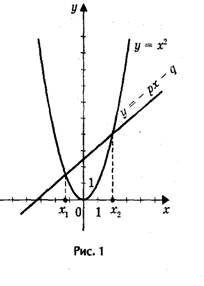
Построим графики зависимости у = х 2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости —
прямая (рис.1). Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квад- ратного уравнения;
— прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
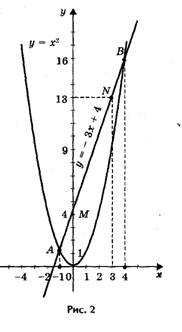
1) Решим графически уравнение х 2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х 2 = 3х + 4.
Построим параболу у = х 2 и прямую у = 3х + 4. Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13). Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1 = — 1 и х2 = 4. Ответ: х1 = — 1;
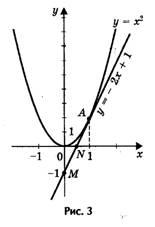
2) Решим графически уравнение (рис. 3) х 2 — 2х + 1 = 0.
Решение. Запишем уравнение в виде х 2 = 2х — 1.
Построим параболу у = х 2 и прямую у = 2х — 1.
Прямую у = 2х — 1 построим по двум точкам М (0; — 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с
абсциссой х = 1. Ответ: х = 1.
3) Решим графически уравнение х 2 — 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х 2 = 5х — 5. Построим параболу у = х 2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х 2 — 2х + 5 = 0 корней не имеет.
http://urok.1sept.ru/articles/414416
http://kazedu.com/referat/167427/3