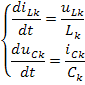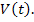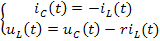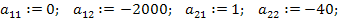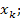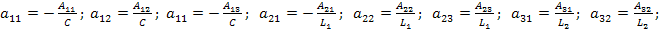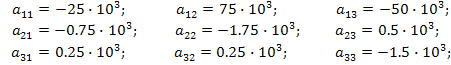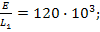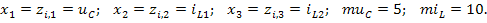Метод переменных состояния уравнения состояния
Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости 

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как 
Пусть в момент времени 



В момент времени t составляющая общего тока, определяемая начальным скачком напряжения 

В момент времени 


Полный ток 


Заменяя конечный интервал приращения времени 
 . . | (1) |
Соотношение (1) называется интегралом Дюамеля.
Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости 
Последовательность расчета с использованием
интеграла Дюамеля
- Определение функции
(или
) для исследуемой цепи.
- Запись выражения
(или
) путем формальной замены t на
.
- Определение производной
.
- Подстановка найденных функций в (1) и интегрирование определенного интеграла.
В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
Исходные данные для расчета: 



 .
. .
.

Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.
Метод переменных состояния
Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.
Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.
Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.
К уравнениям состояния выдвигаются два основных требования:
-возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.
Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.
Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.
При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные 



Таким образом, полная система уравнений в матричной форме записи имеет вид
 ; ; | (2) |
 . . | (3) |
Здесь 







Начальные условия для уравнения (2) задаются вектором начальных значений 
В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи 

По законам Кирхгофа для данной цепи запишем
 ; ; | (4) |
 ; ; | (5) |
 . . | (6) |
Поскольку 
или в матричной форме записи
Матричное уравнение вида (3) вытекает из соотношений (4) и (6):
Вектор начальных значений 

Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.
Методика составления уравнений состояния
Эта методика включает в себя следующие основные этапы:
1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.
2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).
3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.
№74 Расчет переходных процессов методом переменных состояния.
Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.
В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:
Та же система уравнений в матричной форме:
или в обобщённой матричной форме:
Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к-го шага:
Значения производных на к-ом шаге:
Значения переменных на к-ом шаге:
Для определения значений переменных и их производных на 1-м шаге ин¬тегрирова¬ния используются их значения на момент t=0, т.е. их начальные условия x1(0), x2(0). xn(0).
Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются »лишние» переменные, имеющие зависимые начальные условия, и оставляют переменные iL(t) и uC(t), которые не изменяются скачком и имеют независи-мые начальные условия iL(0) и uC(0); б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.
В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений [A] и [B].
Последовательность расчета переходного процесса методом переменных состояния выглядит так:
1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия iL(0) и uC(0).
2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.
3. Методом исключения »лишних» переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.
4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.
5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы x=f(t)или в виде таблицы координат функций для заданных моментов времени.
Пример. Для схемы рис. 74.1 с заданными параметрами элементов (e(t)=Emsin(ωt+ψE), R, R1, R2, R3, L1, L2, C) выполнить расчет переходного процесса и определить функцию uab(t).
1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия i1(0), i2(0), uC(0).
2. Составляется система дифференциальных уравнений по законам Кирхгофа:
3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.
Для этой цели из (1) выражаем
и делаем подстановку в (1) и (2), а из (4) делаем подстановку в (1). Тогда получим:
Подсчитаем значения отднльных коэфициэнтов:
Составляем матрицы коэффициентов:
В качества исследуемого промежутка времени выбираем период переменного тока
Число шагов интегрирования принимаем N = 1000,
Вводим исходные данные в ЭВМ и выполняем рассчет.
В качестве выходной функции принимаем:
Для выходной функции Uab(T) строим графическую диаграмму в интервале периода Т.
Метод переменных состояния
Факультет автоматики и электромеханики
Кафедра теоретической и общей электротехники
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
(Метод переменных состояния)
Методические указания к выполнению курсовой работы
Составил Башев А.А.
Ред. проф. Алтунин Б.Ю.
Н.Новгород, 2010
Метод переменных состояния.
В основу метода переменных состояния положена принципиальная возможность замены дифференциального уравнения n-го порядка электрической цепи n дифференциальными уравнениями первого порядка. В качестве переменных состояния принимают токи индуктивностей 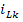
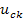
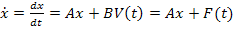
где: 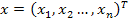
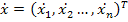
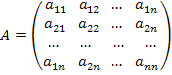
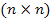
V(t) – столбцовая матрица (вектор) m независимых воздействий;
B – матрица размером 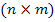
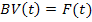
Формирование системы дифференциальных уравнений цепи основано на использовании дифференциальных уравнений для переменных состояния, согласно которым
Расчёт цепей методом переменных состояний можно разделить на два этапа:
1) На первом этапе составляют систему дифференциальных уравнений цепи;
2) На втором этапе решают составленную систему дифференциальных уравнений;
Решение системы дифференциальных уравнений, составленных методом переменных состояния, можно выполнить двумя способами: аналитическим и численным.
При аналитическом способе решение уравнений состояния записывают в виде суммы матриц принуждённой 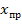
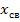
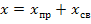
где: 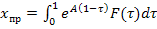
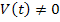

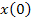
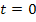
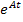
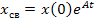
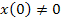
Если в цепи после коммутации нет источников энергии, т.е. 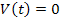
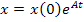
Если же после коммутации есть источники независимых воздействий, то матрица 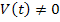
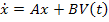
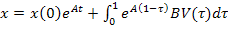
которое состоит из суммы двух слагаемых – реакции цепи при ненулевых начальных условиях и реакции цепи при нулевых начальных условиях и наличии источников внешних воздействий
При численном способе решения уравнений состояния используют различные программы численного интегрирования на ЭВМ: метод Рунге-Кутта, метод Эйлера, метод трапеций и др. Так, например, в пакете программ MathCAD приведены программы численного решения дифференциальных уравнений модифицированном методом Эйлера и методом Рунге-Кутта. Поскольку погрешность решения методом Эйлера достигает нескольких процентов, то более предпочтительным является метод Рунге-Кутта, который при решении уравнений четвёртого порядка даёт погрешность 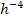
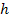
В системе MatchCAD программа интегрирования уравнений по методу Рунге-Кутта имеет имя rkfixed. Обращение к ней производится через операцию присваивания какой-либо переменной (в дальнейшем z) имени программы:
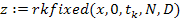
где: x – вектор переменных состояния, размер которого определяется вектором начальных значений 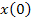
0 и 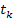
N – число точек на интервале интегрирования;
D – функция, которая описывает правую часть уравнений, разрешённых относительно первых производных.
Для линейных цепей функция D имеет вид линейного матричного преобразования 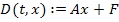
Матрица z имеет размер 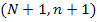
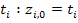
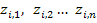
Для контоля правильности задания исходных данных можно (но не обязательно) обратиться к программе определения собственных чисел матрицы A: eigenvals (A). Эта программа выводит информацию о собственных числах, которые совпадают с корнями характеристического уравнения цепи. Необходимым, но недостаточным условием правильности ввода данных, является набор отрицательных собственных чисел (или комплексно-сопряжённых чисел с отрицательно вещественной частью).
Рассмотрим теперь некоторые способы составления дифференциальных уравнений цепи по методу переменных состояния. Для этих целей наиболее часто применяют два основных способа:
1) использование законов Кирхгофа;
2) использование метода наложения.
Рассмотрим применение этих способов на некоторых примерах.
Пример 1. Требуется составить уравнения состояния и решить их для одноконтурной цепи второго порядка при отключении источника напряжения Е. Схема цепи приведена на рисунке 1(а), а параметры её элементов имеют следующие значения: Е=40 В; r=40 Ом; L=1 Гн; С=500мкФ.
Решение. Посмотрим схему замещения цепи для произвольного момента времени t, которая приведена на рисунке 1(б). На этой схеме ёмкость С заменена источником постоянного напряжения 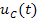
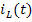
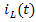
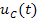
Рисунок 1. Исходная (а) и расчётная (б) схемы цепи к примеру 1.
Для полученной схемы можно составить уравнения, пользуясь законами Кирхгофа:
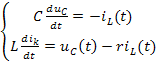
Из этих уравнений получаем значение первых производных переменных состояния:
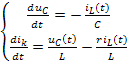
Пользуясь которыми, запишем матричное уравнение цепи:
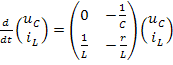
При использовании программы rkfixedэто уравнение записывают в виде:
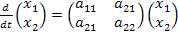
где 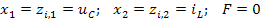
Это матричное уравнение необходимо ещё дополнить матрицей начальных состояний цепи, которая включает напряжение на ёмкости и ток в индуктивности на момент коммутации (т.е. при t=0_):
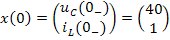
используемой для начала процесса интегрирования дифференциальных уравнений цепи.
Перед обращением к программе интегрирования rkfixed определяем через операцию присваивания значения следующих величин:
1) коэффициентов матрицы А:
2) значений вектора начальных состояний переменных
3) число точек интегрирования 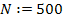
4) формализованную матричную запись уравнений состояния 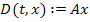
5) конечное значение временного интервала 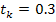
Необходимый временной интервал интегрирования 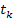
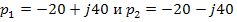
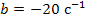
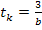
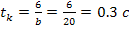
Форма записи исходных данных для программы rkfixed и результаты расчёта приведены на рисунке 2. Поскольку переменные состояния 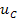
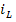
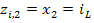
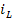
Из полученных графиков следует, что переходный процесс в цепи носит колебательных характер, а обе функции постепенно затухают до нулевого значения при увеличении времени t.
Рисунок 2. Результаты расчёта к примеру 1.
Пример 2. Составить уравнения для переменных состояния и рассчитать их при замыкании ключа К в цепи второго порядка, изображённой на рисунке 3(а). Параметры элементов цепи имеют следующие значения: А; r1=r2=50 Ом; L=5 мГн; С=0,1 мкФ.
Решение. Переходный процесс в рассматриваемой цепи возникает в результате перераспределения энергии между индуктивностью L и ёмкостью C после подключения сопротивления r1. Используя первый закон Кирхгофа, определим ток в ёмкости С:
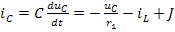
Рисунок 3. Исходная (а) и расчётная (б) схемы к примеру 2.
Аналогично, используя второй закон Кирхгофа, найдём напряжение на индуктивности:
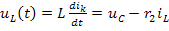
Объединим эти уравнения в систему для переменных состояния:
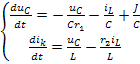
Полученную систему уравнений запишем в матричной форме:
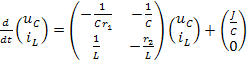
После подстановки числовых значений параметров элементов получим уравнения состояния в виде:
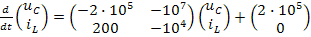
Для определения вектора начальных значений найдём напряжение на ёмкости и ток в индуктивности до замыкания ключа К:
Таким образом, вектор начальных значений переменных состояния имеет вид:
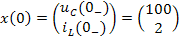
Схемы замещения для расчёта значений переменных состояния приведена на рисунке 3(б). На этой схеме ёмкость заменена источником напряжения 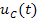
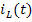
Решение уравнений состояния выполним по программе rkfixed, входящей в систему MathCAD. Для этого присвоим переменным состояния следующие значения: 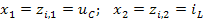
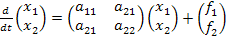
где значения коэффициентов можно взять из уравнений состояния, рассчитанных выше, и включить в программу констант или определить через операции присваивания в самой программе.
Форма задания исходных данных для расчёта по программе rkfixed приведена на рисунке 4. Значение N=5000 указано произвольно, так как оно влияет только на время выполнения расчёта и точность. Косвенно оценить точность расчёта можно, сравнив результаты интегрирования для двух значений N=N1 и N1/2. Если результаты расчета в этих точках совпадают, то точность вычислений и число точек интегрирования на интервале tk находится в приемлемых пределах.
Через операцию присваивания определяем также вектор начальных значений х и вектор независимых источников F. Временной интервал tk может быть указан произвольно или приближённо выбран с помощью анализа чисел матрицы А.
Для апериодического процесса, который существует в рассматриваемой цепи, следует выбрать наименьшее по модулю собственное число pmin и воспользоваться формулой tk =3/pmin. Из двух собственных чисел p1=-1.888E5 1/c; p2=-2.118E4 1/c меньшее значение имеет p2, поэтому tk =3/2,118Е4=1,42Е-4 с.
Выбор интервала tk можно также выполнить, анализируя постоянные времени цепей первого порядка, которые можно построить на основе исходной цепи путём последовательного исключения реактивных элементов. При этом из найденных постоянных времени следует выбрать ту, которая имеет максимальное значение, и, используя её, рассчитать
Графики временных зависимостей 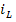
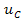
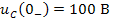
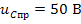

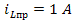
Рисунок 4. Результаты расчёта к примеру 2.
Пример 3. Составить уравнения для переменных состояния и выполнить расчёт переходного процесса в цепи третьего порядка, приведённой на рисунке 5(а) при замыкании ключа К. Параметры элементов цепи имеют следующие значения: Е=120 В; r1=r3=r4=1 Ом; r2=r5=2 Ом; L1=1 мГн; L2=2 мГн; С=10 мкФ.
Рисунок 5. Исходная (а) и расчётная (б) схемы к примеру 3.
Решение. Переходный процесс в схеме обусловлен перераспределением энергии реактивными элементами цепи после коммутации ключа К. На рисунке 5(б) изображена схема замещения цепи, на которой реактивные элементы заменены источниками напряжения и тока. Положительные направления этих источников согласованы с исходной схемой. При расчёте схемы замещения определению подлежат напряжения на источниках тока 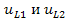
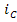
Расчёт схемы, приведённой на рисунке 6(а), позволяет определить искомые величины от действия источника напряжения 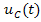
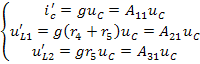
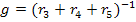
Аналогично выполняется расчёт схемы, изображённой на рисунке 6(б), пользуясь которой, определим те же величины от действия источника тока 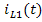
Рисунок 6. Схемы для расчёта цепи от напряжения 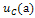
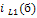

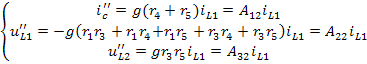
Выполнив расчёт схемы, приведённой на рисунке 6(в), найдём искомые величины при действии 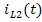
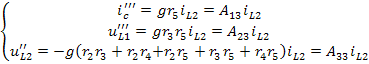
Расчёт схемы, изображённой на рисунке 6(г), позволяет определить искомые величины от действия напряжения Е:
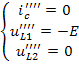
Суммируя частные решения для отдельных источников с учётом выбранных положительных направлений напряжений и токов, находим полные значения искомых величин:
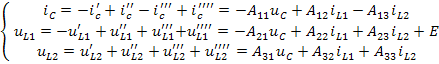
Полученные уравнения позволяют сформулировать нормальную систему дифференциальных уравнений для переменных состояния и записать её в матричной форме:
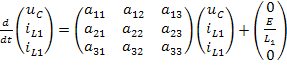
где
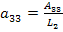
После подстановки значений параметров элементов цепи найдём числовые значения коэффициентов уравнений:
К системе уравнений, записанной в нормальной форме, необходимо добавить вектор, который отражает начальное состояние цепи в момент 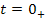
Так как переменные состояния подчиняются законам коммутации, то этот вектор можно получить из анализа состояния цепи до коммутации, т.е. при 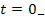
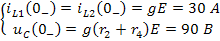
Таким образом, вектор начальных состояний цепи имеет вид:
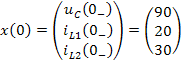
При обращении к программе rkfixed, входящей в систему MathCAD, можно использовать найденные выше значения коэффициентов дифференциальных уравнений или задать их в виде расчётных формул с указанием значений исходных параметров схемы. На рисунке 7 приведён результат расчёта по программе rkfixed. При построении графиков приняты следующие обозначения и масштабные коэффициенты:
Рисунок 7. Результаты к примеру 3.
Кроме этого, при вводе данных указано время интегрирования, которое, как и раньше, выбрано по формуле tk =3/bmin, где bmin – минимальное значение модуля вещественной части собственных чисел матрицы eigenvals (A). Для рассматриваемого примера это число имеет значение b=1.268E3, откуда находим значение tk=2E-3 с.
http://toehelp.com.ua/lectures/074.html
http://mydocx.ru/1-78244.html

 (или
(или  ) для исследуемой цепи.
) для исследуемой цепи. (или
(или  ) путем формальной замены t на
) путем формальной замены t на  .
. .
.