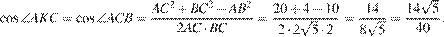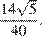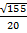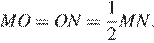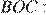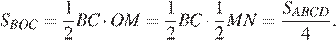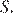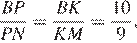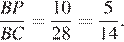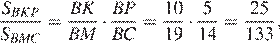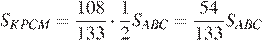Метод площадей при решении систем уравнений

Обучение учащихся 9 классов методу площадей

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выступление на ШМО учителей математики

«Обучение учащихся 9 классов методу площадей при подготовки к ОГЭ по математике»

Составитель: Чугунова Юлия Васильевна

учитель математики и информатики

Решение геометрических задач иногда напоминает трюки иллюзионистов – порой, зная решение задачи, не понимаешь, как можно было до него додуматься. Почти каждая трудная геометрическая задача требует индивидуального подхода. Однако, существуют методы, использование которых ведет к успешному решению многих типов задач. Один из них – метод площадей. Из его названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения, а иногда и системы уравнений.

Зачастую в школьном курсе геометрии авторы учебников не упоминают о данном методе, хотя задачи на применение метода площадей часто используются в ОГЭ (ГИА) и ЕГЭ. Поэтому и существует необходимость в обучении учащихся применению метода площадей при решении геометрических задач.

Методы решения геометрических задач традиционно делят на: геометрические, алгебраические и комбинированные. Метод площадей относим к геометрическим методам, под которыми будем понимать способ познавательной деятельности учащихся, основанный на системе геометрических знаний и на геометрических (наглядных) представлениях.

В настоящее время имеется достаточное число исследований, посвященных обучению учащихся методам решения задач. Так, методика обучения решению задач геометрическими методами раскрывается в работах Г. И. Саранцева, Л. С. Капкаевой, Е. Е. Овчинниковой и др. Совокупность задач, в рамках применения отдельных свойств площади, приведены в различных статьях. Так в статье Новикова в журнале Квант рассматриваются различные методы решения задач, среди которых есть и метод площадей. Он подчеркивает, что его главное достоинство – в его идейной «прозрачно c ти», а также говорит об уникальности и плодотворности этого метода. Однако, в представленных работах не выделяются действия адекватные методу площадей, недостаточно разработаны задачи по обучению каждому действию метода и их совокупности.

Опираясь на имеющиеся исследования, мною было выяснено, что метод площадей составляют следующие действия

1) анализ заданной в задаче конфигурации, включающей в себя анализ ее элементов и их свойств

2) нахождение площади фигуры, используя данные и искомые элементы

3) составление уравнения, используя различные выражения для площади фигуры

4)разбиение фигуры на части

5) нахождение отношения площадей и соответствующих отрезков

Так, для решения следующей задачи необходимо выполнить действия (1-4):

Задача 1 . Найдите биссектрису AD треугольника ABC , если АВ=с, АС= b , а угол А равен  .

Подсчитаем площадь треугольника ABC (рисунок 1):

Тогда, подставляя полученные выражения в (1), имеем уравнение:

Откуда после преобразований получаем:

Решая задачу 2 учащиеся : анализируют заданную в задаче конфигурации, включающую в себя анализ ее элементов и их свойств, находят отношение площадей и соответствующих отрезков.

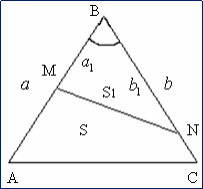
Задача 2. Каждая диагональ четырехугольника делит его на треугольники одинаковой площади. Докажите, что это параллелограмм.

Отметим , что S2:S1= AO: ОС , S4:S3=AO:OC. Кроме этого, соответствующие высоты треугольников BOC, COD и AOB, AOD равны, соответственно, площади относятся как длины оснований. Из того, что S ₁ = S ₃ и S ₂ = S ₄ . следует, что AO: OC =OС: O А. Следовательно, AO = OC. Аналогично можно доказать, что BO = OD . Можно сделать вывод, что диагонали четырехугольника точкой пересечения делятся пополам, а это значит, что ABCD — параллелограмм.

Конечно же, обучать действиям и их совокупностям нужно поэтапно. Мною выделены следующие этапы обучения учащихся методу площадей.

Его цель — актуализировать знания о нахождении площадей различных фигур.

На 2 этапе формируются отдельные компоненты метода (умение находить площадь одной и той же фигуры двумя разными способами, умение разбивать фигуру на части, умение анализировать задачную ситуации и т.д.)

3 этап – формирование умений решать задачи, требующие применения комплекса действий, соответствующих методу .

Приведем цепочку задач для обучения умению решать задачи, составляя уравнение, используя формулы площади треугольника.

В задачах 3-5 используется дважды формула

Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Задача 4. Катеты прямоугольного треугольника равны 3 и 4. Найти высоту, проведенную к гипотенузе данного треугольника.

Задача 5. Сторона основания равнобедренного треугольника равна 8, а боковые стороны равны 10. Найти высоту, приведенную к боковой стороне.

В задачах 6-7 – формулы и СЛ

Задача 6. Дан равнобедренный треугольник АВС, сторона АВ=ВС=10, высота, проведенная к основанию АС равна 6. Найдите радиус вписанной окружности.

Задача 7. В треугольнике АВС, сторона АВ=2, ВС=1,5, С=90. Найдите радиус вписанной окружности.

Задача 8. Найти радиус описанной около треугольника окружности, если его стороны равны 3, 7 и 9.

Заметим, что в полной мере реализовать обучение по предложенной методике целесообразно на элективном курсе.

Мною разработан курс, который рекомендуется проводить в 9 классе, поскольку все основные сведения о площадях фигур получены к концу 8 класса. Вариант тематического плана курса представлен в таблице 1

Понятие площади. Вычисление площадей различных фигур.

Понятие метода площадей. Решение простейших (элементарных) задач метом площадей.

Свойства площадей и применение их при решении планиметрических задач

Далее приведем некоторые задачи, которые можно применять при обучении учащихся методу площадей.

Задача 1. Дан треугольник ABC , сторона ВС равна b , высота AH равна h . Найти площадь этого треугольника. Желательно рассматривать следующие случаи треугольника: 1) остроугольный, 2) тупоугольный, 3) прямоугольный, 4)равнобедренный, 5) равносторонний.

Полезно рассматривать обратные задачи. Например:

Задача 2. Дан треугольник АВС , его площадь равна а , высота AH равна h . Найти сторону ВС данного треугольника.

Приведем одну из цепочек задач, предлагаемых учащимся.

Задача 3. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника (рисунок 11).

Задача 4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника (рисунок 12).

Задача 5. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30 ° (рисунок 13).

Задача 6. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника (рисунок 14).

Задача 7. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30 ° . Найдите боковую сторону треугольника, если его площадь равна 25 (рисунок 15).

Также нужно вспомнить формулы нахождения площади треугольника: , где – радиус вписанной окружности, – полупериметр, формулу Герона: где – полупериметр, – стороны треугольника; формулу, связывающую площадь треугольника с радиусом описанной окружности: , где – стороны треугольника, – радиус описанной окружности.

На втором этапе у учащихся формируется умение находить площадь одной и той же фигуры двумя разными способами, составлять уравнение и решать его.

Задача 8. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне (рисунок 16)?

Задача 9. Катеты прямоугольного треугольника равны 3 и 4. Найти высоту и гипотенузу данного треугольника (рисунок 17).

Задача 10. Сторона основания равнобедренного треугольника равна 8, а боковые стороны равны 10. Найти высоту, приведенную к боковой стороне (рисунок 18).

Следующие задачи связаны с нахождением площади треугольника двумя способами:

Задача 11. Дан равнобедренный треугольник АВС , сторона АВ = ВС =10, высота, проведенная к основанию АС равна 6. Найдите радиус вписанной окружности.

Задача 12. В треугольнике АВС , сторона АВ =2, ВС =1,5, С =90. Найдите радиус вписанной окружности.

Задача 13. Стороны треугольника равны 5 и 7, угол между ними 60. Найти высоту треугольника, проведенную к третьей стороне.

Задача 14. Найти радиус описанной окружности около треугольника со сторонами 3, 7 и 9.

Задача 15. Найдите радиус окружности, описанной около треугольника со сторонами 3, 7, 2.

Также на втором этапе у учащихся формируются умения использовать аддитивность площадей при решении задач ( анализировать заданную в задаче конфигурацию, включающей в себя анализ ее элементов и их свойств, разбивать фигуру на части, вычислять ее площадь).

Так, можно предложить учащимся задачу, в которой используется свойство аддитивности площади.

Задача 16. Доказать, что в равнобедренном треугольнике АВС ( АВ=ВС ) сумма расстояний от любой точки К отрезка АС до сторон АВ и ВС есть величина постоянная (рисунок 19).

Приведем фрагмент занятия, как учитель после построения чертежа может направить работу учащихся на усвоение способа решения задачи.

Учитель: Что дано в условии задачи?

Ученик: Равнобедренный треугольник и точка на его основании.

Учитель: На сколько треугольников разделен треугольник ABC отрезком ВК ?

Ученик: Треугольник разделен отрезком ВК на два треугольника.

Учитель: Какие данные относятся к треугольникам разбиения?

Ученик: В каждом из них из точки К проведена высота.

Учитель: К каким сторонам равнобедренного треугольника проведены

Ученик: Высоты проведены к боковым сторонам треугольника.

Учитель: Какую высоту лучше провести в треугольнике ABC ?

Ученик: Проведем высоту к боковой стороне.

Учитель: Правильно, например, из точки С проведем высоту СН .

Учитель на доске, а ученики в тетрадях проводят высоту СН .

Учитель: Какие свойства площади можно использовать для решения

Ученик: Площадь всего треугольника равна сумме площадей его частей – треугольников АВК и ВКС

Учитель: Запишите данное условие в математической форме.

Учитель: Как именно формулы площади подойдут в этой ситуации?

Ученик: Формула, выражающая площадь треугольника через его высоту и основание.

Учитель: Правильно, найдем площади треугольников ABC , АВК и СВК .

Учитель на доске, а ученики в тетрадях записывают , , .

Учитель: Подставим найденные значения в записанное нами условие.

На доске и в тетрадях появляется запись:

Учитель: Мы знаем, что по условию задачи . В записанном нами выражении заменим на .

Учитель записывает на доске, а ученики в тетради:

Учитель: Мы выяснили, что сумма расстояний от любой точки К на основании равнобедренного треугольника равна высоте этого треугольника, проведенной к боковой стороне, т.е. одна и та же.

Особое внимание при этом следует уделять всестороннему изучению заданной в задаче конфигурации, включающему в себя анализ ее элементов и их свойств, так как именно разбиение фигуры на части и работа с этими частями вызывает трудности у школьников.

Задачи 17-18 решается аналогично. При решении каждой из задач учитель должен обсуждать с учащимися целесообразность выбора метода площадей для решения задачи.

Задача 17 . На продолжении основания АС равнобедренного треугольника ABC выбрана точка М , удаленная от прямой АВ на расстояние а и от прямой ВС на расстояние с ( а > с ). Найдите высоту треугольника, проведенную к боковой стороне.

Задача 18. В прямоугольный треугольник, катеты которого равны 10 и 15, вписан квадрат, имеющий с ним общий угол. Найдите сторону квадрата

Задача 19. Из точки, взятой на гипотенузе прямоугольного треугольника, проведены перпендикуляры на оба катета. Определите площадь прямоугольника, отсеченного этими перпендикулярами, если отрезки катетов при вершинах острых углов треугольника равны т и п.

Задача 20 . Сумма длин катетов прямоугольного треугольника равна 14, а площадь вписанного в него квадрата, одна из вершин которого совпадает с вершиной прямого угла треугольника, равна . Найдите периметр треугольника.

На третьем этапе учащиеся применяют полученные знания о методе площадей, решая наиболее сложные задачи.

Работа с задачами 17-20 начинается с анализа чертежа. Замечаем, что две стороны вписанного квадрата или прямоугольника перпендикулярны сторонам данного треугольника, то есть можно разбить данный треугольник на два треугольника, в которых эти стороны будут высотами. Тогда, исходя из анализа условия задачи, можно сделать вывод, что легко вычислить площадь данного треугольника двумя способами: по данным задачи и через эти неизвестные высоты и соответствующие им основания в треугольниках.

Задача 21 . Через центр правильного треугольника проведена прямая, параллельная основанию. На этой прямой взята произвольная точка М . Докажите, что расстояние от точки М до основания треугольника есть полусумма расстояний от точки М до боковых сторон треугольника.

В задаче 21 необходимо заметить, что расстояние от точки, взятой на прямой, параллельной основанию треугольника, до основания треугольника постоянно, в этой задаче оно равно трети высоты треугольника.

На третьем этапе учащиеся применяют полученные знания о методе площадей, решая наиболее сложные задачи, используют свойства отношения площадей.

В следующей задаче поможет вычисление катетов треугольника. Покажем ее полное решение.

Задача 22 . Точка пересечения медиан прямоугольного треугольника удалена от катетов на расстояния соответственно 3 и 4. Найдите расстояние от этой точки до гипотенузы (рисунок 20).

Пусть М — точка пересечения медиан прямоугольного треугольника A ВС с катетами АС и ВС, Р и Q — проекции точки М на АС и ВС соответственно, MP =3, МО =4, К – середина ВС .

Поскольку медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины треугольника, то . Поэтому . Аналогично . Тогда .

С другой стороны,

, – искомое расстояние. Следовательно, .

Задача 23 . Два квадрата со стороной а имеют общую вершину, причем сторона одного из них лежит на диагонали другого. Найдите площадь обшей части этих квадратов

Задача 24 . Внутри прямого угла О дана точка М , расстояния которой от сторон угла равны 4 см и 8 см. Прямая, проходящая через точку М , отсекает от прямого угла треугольник АОВ с площадью 100 см 2 . Найдите катеты треугольника.

Задача 25 . Основания трапеции равны а и b . Отрезок с концами на боковых сторонах трапеции, параллельный основаниям, разделяет трапецию на две трапеции, площади которых равны. Найдите длину этого отрезка.

Задача 26 . Через вершину треугольника проведите две прямые, которые разделят его на три треугольника равной площади.

Задача 27 . Разделить данный треугольник АВС ломаной АМК на три равных по площади части (рисунок 21).

Задача 28. Вычислите площадь треугольника АВС , если площадь треугольника АСК равна S (рисунок 22).

«Метод площадей при решении геометрических задач второй части ОГЭ».

Тема: «Метод площадей при решении геометрических задач второй части ОГЭ».

Цель: Рассмотрение теоретических основ;
Формирование представления о методе площадей;
Использование метода площадей при решении планиметрических (второй части ОГЭ и некоторых конкурсных) задач.

Предмету геометрия отведено по учебному плану меньше часов, чем алгебре. Учащиеся испытывают трудности при выполнении геометрических заданий. Это задачи повышенной трудности, в модуле «Геометрия» на ОГЭ. Тема «Метод площадей» — актуальна в связи с решением таких задач на экзамене (как №24, №25, №26)
и на различных олимпиадах и конкурсах.

II. Основная часть.

1. Метод площадей.

2. Определение метода площадей. Характеристики метода.

3. Основные свойства площадей и ключевые задачи.

4. Практический диапазон применимости метода площадей к решению задач

V. Приложение. Причины ошибок. Классификация

Определение проблемы: необходимость разбора решения геометрических задач из второй части экзаменационной работы по выбранному методу.

1. Изучение научно-методической литературы по проблеме исследования.

Изучение метода площадей и после определения проблемы научиться применять свойства площадей для составления соотношений, связывающих ключевые задачи с неизвестными, используя различные приёмы.

2. Анализ различных учебных пособий с целью изучения и описания метода площадей.

3. Рассмотрение некоторого диапазона применимости метода площадей к решению задач.

4. Рассмотрение на примерах структуры процесса решения таких задач и развитие умения самостоятельно анализировать и конструировать свои знания; классифицировать задачи.

5. Умение ориентироваться в планиметрическом пространстве и нахождение путей решения.

Трудности решения геометрических задач обусловлены следующими факторами:
Неалгоритмичность задач.
Необходимость выбора метода решения задачи и теоремы для решения конкретной задачи из большого набора известных фактов.

Обсуждение методов исследования. Метод конкретных ситуаций (следование принципу «процесс обсуждения важнее самого решения»), самостоятельное изучение и подготовленное в письменном виде решение проблемы.

Сбор, анализ полученных данных, систематизация решенных задач, корректировка их. Оформление результатов исследовательской работы в электронном виде.

1. Метод площадей.

В школьном курсе математики, самыми трудными считаются

геометрические задачи. Как научиться решать геометрические задачи,

особенно сложные, конкурсные? При решении геометрических задач, как

правило, алгоритмов нет, и выбирать наиболее подходящую к данному

случаю теорему не просто.

В данной работе рассматривается один из самых распространенных

алгоритмов решения геометрических задач – метод площадей. Значимость метода площадей заключается в том, что он является предметом изучения и одновременно средством для изучения последующего материала.

Методы решения планиметрических задач. (Дополнительный материал).

Некоторые методы решения геометрических задач (№24, 25, 26)

· Метод дополнительных построений

· Метод вспомогательной окружности.

· Также возможно использование векторного способа на плоскости, возможно использование координатного способа. Учащийся не ограничен в выборе метода решения этих задач.

Геометрические задачи повышенной сложности ОГЭ

В работах на примерах решения конкретных задач обычно используются такие методы:

1. Удвоение медианы

2. Использование введения буквенных обозначений величин

3. Метод вспомогательных построений

4. Построение вспомогательных отрезков в трапеции

5. Использование осевой симметрии

6. Переход к равновеликой вспомогательной фигуре

7. Метод площадей.

8. Введение вспомогательной окружности.

(См. в презентации ключевые задачи)

4. Построение вспомогательных отрезков в трапеции

5. Использование осевой симметрии

6. Переход к равновеликой вспомогательной фигуре

7. Метод площадей.

8. Введение вспомогательной окружности.

(См. в презентации ключевые задачи)

Рассмотрим в нашем исследовании метод площадей.

2. Определение метода площадей. Характеристики метода.

Из названия следует, что главным объектом данного метода является площадь.

Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры.

1. Весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное.
Здесь и проявляется основная особенность метода площадей:
из геометрической задачи он «делает» её алгебраической, сводя всё к решению уравнения (а иногда и системы уравнений).

2. Одна из разновидностей метода площадей сводится к использованию в задаче свойства аддитивности площади: если фигура разбита на части, то ее площадь равна сумме площадей этих частей. S=S1+S2+S3

2. Универсального метода для решения всех задач на площади

многоугольников нет, но существуют приемы, применимые ко многим

задачам. Понятие площади мы используем даже при решении тех задач,
в условии которых отсутствует упоминание площади. Поэтому можно

говорить о методе площадей в геометрии.

4. Метод площадей состоит в применении различных её свойств для нахождения соотношений, связывающих их с неизвестными.

Остановимся подробнее на характеристике и диапазоне применимости метода площадей.

3. Основные свойства площадей

Свойство 1. Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться.

Доказательство:

Рассмотрим ▲ABC и ▲ADC. Они

имеют общее основание и равные

высоты, т.к. прямые AC и BD

параллельные, то расстояние между

ними равно h — высоте ▲ABC и ▲ADC.

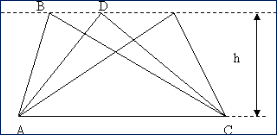
Свойство 2. Если два треугольника имеют одинаковые высоты, то отношение их

площадей равно отношению длин оснований, т. е. сторон,
на которые опущены эти высоты.

Пусть h1 = h2 в двух треугольниках

с основаниями a и b.

Рассмотрим отношение площадей

этих треугольников, получим:

= .

Если два треугольника имеют общий угол, то их площади относятся

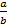
как произведение сторон, заключающих этот угол.

Рассмотрим ▲ABC и ▲MBN.

Пусть AB = k∙MB, BC = k∙NB и ABC=MBN .

Используя формулу площади треугольника, получим: отношение подобных площадей ▲ABC и ▲MBN.

Тогда получим: = k 2 .

Медиана треугольника делит его на две равновеликие части.

Рассмотрим ▲ABC . Пусть

медиана — BM , тогда

AM=MC=1/2AC. Медиана делит

треугольник на два равновеликих с одинаковой

высотой. Найдем площади

Медианы треугольника делят

его на три равновеликие части.

Медианы треугольника делят его
на 6 равновеликих частей.

Утверждение. Два треугольника
являются равновеликими,

если равны их высоты и основания.

Средние линии треугольника площади S

отсекают от него

треугольники площади ¼ S.

Рассмотрим ▲ABC. NM — средняя линия

в треугольнике и она равна половине

Если SABC = S, то можно доказать, что

площади всех треугольников равны

одной четвертой части площади ▲ABC.

4. Применение свойств метода площадей к решению задач.

В данном пункте рассмотрим систему геометрических задач, решаемых методом площадей. Задачи построены по нарастающему уровню сложности.

№1( Задания типа № 24).

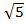
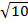
Сто­ро­ны AC, AB, BC тре­уголь­ни­ка ABC равны 2 , и 2 со­от­вет­ствен­но. Точка K рас­по­ло­же­на вне тре­уголь­ни­ка ABC , причём от­ре­зок KC пе­ре­се­ка­ет сто­ро­ну AB в точке, от­лич­ной от B. Из­вест­но, что тре­уголь­ник с вер­ши­на­ми K, A и C по­до­бен ис­ход­но­му. Най­ди­те ко­си­нус угла AKC, если ∠ KAC > 90°. Найти площадь треугольника АВС.

Рассмотрим по­доб­ные тре­уголь­ни­ки ABC и AKC и уста­но­вим со­от­вет­ствие между их углами. Про­тив боль­шей сто­ро­ны все­гда лежит боль­ший угол, в тре­уголь­ни­ке ABC это угол ABC в тре­уголь­ни­ке , в свою очередь, есть тупой угол и он яв­ля­ет­ся наибольшим, зна­чит, ∠ КАС = ∠ АВС. Угол АСК за­ве­до­мо не может быть равен углу так как он со­став­ля­ет толь­ко его часть. Сле­до­ва­тель­но, угол АСВ равен углу АКС.

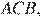
Найдём ко­си­нус угла 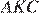, ис­поль­зуя тео­ре­му косинусов:

1)

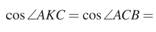
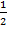
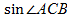
2) S _ABC = • СА • СВ • ;

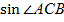
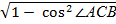
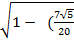
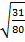
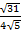
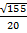
Найдём: = ; ) 2 = = = . S _ABC =

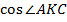
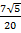
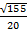
Ответ : = ; S _ABC = .

Задания типа № 25.

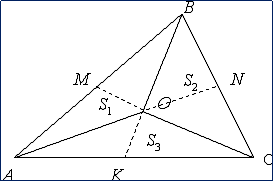
№2. В па­рал­ле­ло­грам­ме ABCD диа­го­на­ли AC и BD пе­ре­се­ка­ют­ся в точке O. До­ка­жи­те, что пло­щадь па­рал­ле­ло­грам­ма ABCD в че­ты­ре раза боль­ше пло­ща­ди тре­уголь­ни­ка BOC.

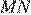
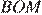
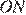
Проведём вы­со­ту так, чтобы она про­хо­ди­ла через точку О. Углы и равны друг другу как вертикальные. Вспом­ним также, что диа­го­на­ли де­лят­ся точ­кой пе­ре­се­че­ния пополам, следовательно, Рас­смот­рим тре­уголь­ни­ки и , они прямоугольные, имеют рав­ные углы и рав­ные гипотенузы, сле­до­ва­тель­но, эти тре­уголь­ни­ки равны, а зна­чит, равны от­рез­ки и . Таким образом,

Площадь па­рал­ле­ло­грамм равна 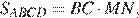а пло­щадь тре­уголь­ни­ка

В тре­уголь­ни­ке ABC на его ме­ди­а­не BM от­ме­че­на точка K так, что BK : KM = 10 : 9. Прямая AK пе­ре­се­ка­ет сто­ро­ну BC в точке P. Найдите от­но­ше­ние пло­ща­ди четырёхугольника KPCM к пло­ща­ди тре­уголь­ни­ка ABС.

Пусть площадь треугольника 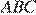равна

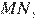
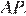
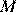
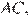
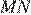
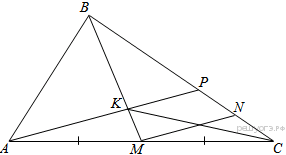
Проведём прямую параллельную Точка — середина следовательно, — средняя линия треугольника значит,

По теореме Фалеса для угла находим:

а так как получаем, что

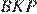
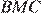
Стороны треугольников и сонаправлены, их площади относятся как произведение отношений сонаправленных сторон,
поэтому

откуда , в то время как следовательно,

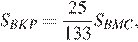
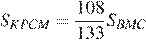
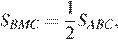
Тем самым, для искомого отношения площадей имеем:.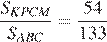

Ответ. .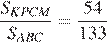

Олимпиадные задачи: 9 класс.

1. Сторона KP трапеции NMКP равна 3 см. Расстояние из вершин N и М до стороны КР равны 7см и 5 см соответственно. Найдите площадь трапеции NMКP.

Решение. Сделаем чертеж. Опустим перпендикуляры из точек N и М на сторону КР и построим перпендикуляр KH к стороне NP .

Презентация на тему: геометрический метод решения систем уравнения

Геометрический метод решения систем уравнений Морозова Татьяна, МДМ-110

Метод — способ достижения какой-либо цели, решения конкретной задачи; совокупность приемов или операций практического или теоретического освоения (познания) действительности. Геометрический метод характеризуется как «метод, идущий от наглядных представлений» (А. Д. Александров), «метод геометрической наглядности» (Г. Фройденталь). Существенными признаками этого понятия являются геометрические (наглядные) представления и законы геометрии, в которых отражены свойства геометрических фигур. Геометрический метод будем понимать как способ познавательной деятельности, основанный на системе геометрических знаний и на геометрических (наглядных) представлениях.

Геометрические методы: метод длин (свойства длины отрезка); метод треугольников (система знаний о треугольниках); метод параллельных прямых (о параллельных прямых); метод соотношения между сторонами и углами треугольника (о соотношениях между сторонами и углами треугольника); метод четырехугольников (о четырехугольниках); метод площадей (о площади многоугольника); метод подобия треугольников (о подобных треугольниках); тригонометрический метод (о решении треугольников); метод окружностей (об окружности и ее элементах); метод геометрических преобразований ( о геометрических преобразованиях на плоскости и в пространстве); графический метод (о геометрическом представлении элементарных функций).

Метод уравнений состоит из следующих приемов: прием, основанный на составлении и решении линейного уравнения («прием линейного уравнения») ; прием квадратного уравнения; прием рационального уравнения; прием системы двух линейных уравнений с двумя переменными и др.

Геометрическое решение негеометрических задач (систем уравнений) Теорема Пифагора Векторный способ Формула расстояния между точками