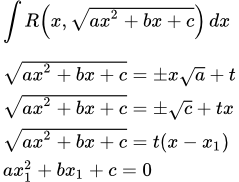Метод подстановки для уравнений эйлера

Подстановки Эйлера. Интегрирование квадратичных иррациональностей с помощью первой подстановки Эйлера.

В этой теме мы рассмотрим вычисление неопределённых интегралов с помощью подстановок Эйлера. На данной странице размещены примеры использования первой подстановки Эйлера, а второй и третьей подстановкам посвящена вторая часть темы.

Нам понадобится таблица неопределенных интегралов, а также таблица производных. Начнём с постановки задачи. Задана некая рациональная функция от $x$ и $\sqrt$, т.е. $R\left(x, \sqrt\right)$. Требуется найти неопределённый интеграл этой функции, т.е. $\int R\left(x, \sqrt\right)dx$. Кстати, если словосочетание «рациональная функция» вызывает вопросы, советую глянуть примечание. Если же нет – пойдём далее.

Что такое рациональная функция: показать\скрыть

Под рациональной функцией (рациональной дробью) понимают отношение двух многочленов любого количества переменных. Например, некая рациональная функция от переменной $x$ может иметь вид $R(x)=\frac<5x^2+10x-1><58x^<14>+9>$. А рациональная функция от переменных $u$ и $v$ может может принять такой вид: $R(u,v)=\frac<4u^2v-v^3+2><5u^3-9u^5v^9+7v>$.

Если говорить совсем уж неформально, рациональная функция от каких либо параметров представляет собой дробь. Оная дробь может содержать только такие слагаемые, в которых присутствует произведение упомянутых параметров и возведение их в неотрицательную целочисленную степень. Например, рациональная дробь от переменных $tigr$, $kot$ и $volk$ может иметь такой вид: $R(tigr, kot, volk)=\frac<5volk-4kot^5tigr^6volk^3+8kot^7+4><4tigr^3+7volk^7+2tigr^2 volk>$.

Ну, а рациональная дробь от $x$ и $ \sqrt$ может содержать лишь выражения вида $a_1\cdot\ x^\cdot \left(\sqrt\right)^$, где $a_1$ – любое действительное число, $a_2$ и $a_3$ – неотрицательные целые числа. Например, $R\left(x, \sqrt\right)=\frac<5x^2+4x\cdot \sqrt><2\left(\sqrt\right)^5+8x^8-1>$.

Суть подстановок Эйлера сводится к трём правилам:

Использование знака «$\pm$» означает, что решающий вправе взять любой знак (плюс или минус) – на своё усмотрение. Например, если $a > 0$, то можно принять $\sqrt=-\sqrt\; x+t$, а можно взять $\sqrt=\sqrt\; x+t$.

Стоит отметить, что применение одной подстановки Эйлера не исключает другую. Например, для корня $\sqrt<5x^2+2x+100>$ можно использовать как первую подстановку (ибо $5 > 0$), так и вторую (так как $100 > 0$). Обычно используют первую подстановку, применение которой мы рассмотрим на данной странице. Применению второй и третьей подстановок Эйлера посвящены примеры в второй части.

Вообще, подстановки Эйлера часто приводят к громоздким преобразованиям, поэтому их в основном применяют тогда, когда вычислить интеграл иным способом уже не удаётся.

Подынтегральная функция $\frac<1><\sqrt<4x^2+12x+15>>$ является рациональной функцией от $\sqrt<4x^2+12x+15>$, посему можем использовать подстановки Эйлера. Так как коэффициент перед $x^2$ больше нуля (т.е. $4 > 0$), то используем первую подстановку Эйлера. В записи первой подстановки участвует знак «$\pm$», означающий, что можно избрать как «+», так и «–». Для совершения столь ответственного выбора я подкинул монетку и выбрал минус 🙂

Что нам необходимо для того, чтобы использовать новую переменную $t$? Нам нужно выразить старую переменную (т.е. $x$) через новую. Возведём в квадрат обе части последнего равенства:

Теперь перебросим $-4xt$ в левую часть полученного равенства, а $15$ – в правую часть. После этого выразим $x$ через $t$:

Кстати сказать, теперь уже легко заменить $\sqrt<4x^2+12x+15>$, расположенный под интегралом. Вспоминая, что согласно сделанной замене $\sqrt<4x^2+12x+15>=-2x+t$, мы получим следующее:

Последним элементом, подлежащим замене, является $dx$. Так как $dx=x’dt$, получим:

Подводя итоги, запишем полученные результаты замен для корня и $dx$:

Осуществим замену в исходном интеграле, подставляя в него полученные выражения:

Вспоминая, что $t=\sqrt<4x^2+12x+15>+2x$, получим:

Ответ получен. Кстати сказать, этот же пример можно решить гораздо быстрее, применяя готовую формулу №10 из таблицы неопределенных интегралов. Подогнать заданный в условии интеграл под формулу №10 несложно – нужно всего лишь выделить квадрат в подкоренном выражении:

Замечаете, насколько сократился объём решения? 🙂 Это наглядная иллюстрация к вопросу о громоздкости подстановок Эйлера. Если их можно избежать, то их стараются избегать. И такой момент: при желании можно показать, что выражение под модулем положительно, поэтому знак модуля можно убрать. Так как этот вопрос несущественный, я вынесу его под примечание.

Почему можно убрать модуль? показать\скрыть

Наше выражение под модулем имеет такую структуру: $\sqrt+u$, где $u=2x+3$. Если $u ≥ 0$, то неравенство $\sqrt+u > 0$ очевидно.

Проверим, какой знак имеет выражение $\sqrt+u$ если $u u^2$. Обе части этого неравенства положительны, поэтому смело можем извлечь квадратный корень из обеих частей оного неравенства:

Так как $\sqrt=|u|$, то имеем:

Итак, выражение $\sqrt+u$ будет больше нуля, какие бы значения не принимала переменная $u$, посему

Подынтегральная функция $\frac<1>>$ является рациональной функцией от $\sqrt$ и $x$, посему можем использовать подстановки Эйлера. Так как коэффициент перед $x^2$ больше нуля (т.е. $1 > 0$), то используем первую подстановку Эйлера. В записи первой подстановки участвует знак «$\pm$», означающий, что можно избрать как «+», так и «–». В предыдущем примере был избран знак «минус», посему, сугубо для разнообразия, используем знак «плюс»:

Вновь, как и в предыдущем примере, возводим обе части полученного равенства в квадрат и выражаем переменную $x$ через $t$:

Теперь осталось выразить корень $\sqrt$ через новую переменную $t$. Также необходимо найти $dx$:

Подставляя выражения для $x$, $\sqrt$ и $dx$ в исходный интеграл, будем иметь:

Под интегралом мы получили рациональную функцию от переменной $t$. Однако полученная нами рациональная дробь $\frac<-2t^2+2t-2><(1-2t)(t-2)>$ является неправильной, ибо степень многочлена в числителе (т.е. 2) не меньше степени многочлена в знаменателе (которая тоже равна 2). Чтобы получить правильную дробь, для начала раскроем скобки в знаменателе, а потом домножим и числитель и знаменатель на $(-1)$:

Вообще-то, в таких ситуациях положено делить многочлен в числителе на многочлен в знаменателе, используя, например, деление в столбик. Но в нашем случае проще поступить по-иному. Сделаем в числителе простое преобразование: вычтем и прибавим $3t$:

Теперь разложим дробь $\frac<3t><2t^2-5t+2>$ на элементарные. Как это делается, подробно расписано тут.

Окончательно для подынтегральной дроби получим:

Возвращаясь к нашему интегралу, будем иметь:

Вспоминая, что $t=\sqrt-x$, получим:

Подынтегральная функция $\frac<1>\right)>$ является рациональной функцией от $\sqrt$ и $x$, посему можем использовать подстановки Эйлера. Так как коэффициент перед $x^2$ под корнем больше нуля (т.е. $1 > 0$), то используем первую подстановку Эйлера. В записи первой подстановки участвует знак «$\pm$», означающий, что можно избрать как «+», так и «–». В предыдущем примере был избран знак «плюс», посему здесь используем знак «минус»:

Подробные пояснения были даные ранее, посему тут укажем решение практически без комментариев. Я бы советовал этот пример решить читателю самостоятельно, лишь сверяя своё решение с изложенным ниже.

Подставляя полученные выражения в исходный интеграл, будем иметь:

«Хорошие» подстановки закончились. Подставим просто пару чисел, например, $t=2$ и $t=-2$:

$$ t=2; \;\; 10=9A_1+18A_2+18A_3+6A_4+2A_5;\\ t=-2; \;\; 10=9A_1+6A_2-2A_3+18A_4-18A_5. $$

Подставляя в полученные равенства значения $A_1=2$, $A_3=1$, $A_5=-1$, получим систему уравнений:

Решая эту систему методом Крамера или простым «школьным» способом сложения (после вычитания из первого уравнения утроенного второго легко найти значение $A_4$), получим: $A_2=-1$, $A_4=-1$. Итак:

Переходя к интегралу, будем иметь:

В принципе, уже сейчас можно подставить $t=\sqrt+x$ и получить готовый ответ. Однако с целью небольшого упрощения формы ответа, сделаем кое-какие преобразования перед подстановкой:

Полученное выражение несколько проще по сравнению с тем, что мы получили бы, если бы сразу, без преобразований, подставили $t=\sqrt+x$. Ответ был бы тоже верным, но более громоздким.

Примеры на применение второй и третьей подстановок Эйлера рассмотрены во второй части.

Подстановки Эйлера

Три подстановки Эйлера

Рассмотрим интегралы, подынтегральное выражение которых является рациональной функцией от переменной интегрирования и квадратного корня из квадратного многочлена.
,

Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
, при a > 0 ;
, при c > 0 ;
, где x ₁ – любой корень уравнения a x 2 + b x + c = 0 . Если это уравнение имеет действительные корни.

Также можно применять подстановки:
, при a > 0 ;
, при c > 0 ;

которые отличаются изменением знака перед t .

Выбор подстановки Эйлера

Как видно, для вычисления интеграла, можно применять не одну подстановку Эйлера. Все они приводят к интегралу от рациональной функции. Выбор в пользу той или иной подстановки следует делать, чтобы упростить вычисления.

Так, если подынтегральное выражение содержит комбинацию , то следует выбрать подстановку Эйлера:
.
Поскольку в этом случае сразу получается более простое выражение:

А если подынтегральное выражение содержит комбинацию , то следует выбрать подстановку:
.
Поскольку в этом случае:

Доказательство

Докажем, что подстановки Эйлера приводят к интегралу от рациональной функции.

1) a > 0

Пусть a > 0 . Делаем подстановку:

Возводим в квадрат.

Вычитаем из обеих частей равенства ax 2 и преобразовываем.

Отсюда видно, что x является рациональной функцией от t

Также и дифференциал dx будет произведением рациональной функции от t на dt . И квадратный корень

– тоже рациональная функция от t .

То есть, при такой подстановке, подынтегральное выражение будет рациональной функцией от переменной интегрирования t .

2) c > 0

Пусть c > 0 . Делаем подстановку:

Возводим в квадрат.

Вычитаем из обеих частей равенства c и делим на x .

Отсюда видно, что x является рациональной функцией от t

Также и дифференциал dx будет произведением рациональной функции от t на dt . И квадратный корень

– тоже рациональная функция от t .

То есть, при такой подстановке, подынтегральное выражение будет рациональной функцией от переменной интегрирования t .

3) Уравнение имеет действительные корни

Пусть уравнение a x 2 + b x + c = 0 имеет действительные корни x ₁ , x ₂ . Тогда
a x 2 + b x + c = a ( x – x ₁ )( x – x ₂)
Делаем подстановку:

Возводим в квадрат.

Делим на x – x ₁ и преобразовываем.

Отсюда видно, что x является рациональной функцией от t

Также и дифференциал dx будет произведением рациональной функции от t на dt . И квадратный корень

– тоже рациональная функция от t .

То есть, при такой подстановке, подынтегральное выражение будет рациональной функцией от переменной интегрирования t .

Пример применения подстановки Эйлера

В качестве примера, вычислим интеграл

применяя одну из подстановок Эйлера.

Здесь a = 1 > 0 . В соответствии со сказанным выше, для решения примера, выбираем подстановку:

Поскольку при такой подстановке, подынтегральное выражение сразу упростится

Возводим в квадрат и преобразовываем.

Берем дифференциал.

Преобразуем знаменатель.

Разложим дробь на простейшие. Ищем разложение в виде:

Умножаем на t (2 t + 1) 2

Подставляем t = 0, t = –1/2, t = – 1 .
2 = A

2 = A – B + C
Отсюда
А = 2

C = 2 – A + B = 2 – 2 – 3 = – 3
Итак, мы получили разложение дроби на простейшие:

Интегрируем

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 28-12-2014

2.4. Подстановки Эйлера

Предварительно изучите по учебнику Г. М. Фихтен-гольиа главу X, п° 170.

В задачах 228—233 вычислить интегралы от биномиальных дифференциалов, предварительно определив, к какому случаю каждый из них относится.

Очень важный класс интегралов:

приводится к интегралам от рациональных функций с помощью следующих трех подстановок Эйлера.

I. Если а> 0, то берется подстановка

II. Если с> О, то берется подстановка

III. Если квадратный трехчлен имеет различные вещественные корни , т. е. если

то берется подстановка

Подстановки Эйлера часто приводят к весьма громоздким выкладкам, поэтому их следует применять лишь тогда, ксгда трудно подыскать другой способ для вычисления заданного интеграла.

234. Найти интеграл:

Решение. Здесь а— I, с=2; следовательно, с одинаковым успехом можно применить как первую, так и вторую подстановки Эйлера. Применим первую подстановку Эйлера:

Возводим в квадрат, делаем приведение подобных:

Подставив в данный интеграл, получим:

Мы получили в результате интеграл от рациональной дроби (случай 2), знаменатель которсй содержит множители первой степени, один из которых повторяется дважды. Пишем разложение на простейшие дроби:

235. Найти интеграл:

поэтому применим вторую подстановку Эйлера:

Далее возводим в квадрат, делаем приведение подобных и сокращаем на х:

Замечание. Интеграл в задаче 235 берется гораздо проще подстановкой

Убедитесь в этом сами.

236. Найти интеграл:

Решение. Квадратный трехчлен имеет. здесь два оазличных вещественных корня: Так как

Поэтому применяем третью подстановку Эйлера:

После возведения в квадрат и сокращения на х, получим:

Таким образом, имеем:

В задачах 237—240 вычислите интегралы с помощью одной из подстановок Эйлера.