Метод последовательных приближений решения дифференциального уравнения
Пусть требуется найти решение дифференциального уравнения
Будем предполагать, что в некотором прямоугольнике для уравнения (1) выполнены условия а) и б) теоремы существования и единственности решения задачи (1)-(2).
Решение задачи (1)-(2) может быть найдено методом последовательных приближений , который состоит в следующем.
Строим последовательность функций, определяемых рекуррентными соотношениями
В качестве нулевого приближения можно взять любую функцию, непрерывную в окрестности точки , в частности — начальное значение Коши (2). Можно доказать, что при сделанных предположениях относительно уравнения (1) последовательные приближения сходятся к точному решению уравнения (1), удовлетворяющему условию (2), в некотором интервале , где
Оценка погрешности, получаемой при замене точного решения n-м приближением , даётся неравенством
где . Применяя метод последовательных приближений, следует остановиться на таком , для которого не превосходит допустимой погрешности.
Пример 1. Методом последовательных приближений найти решение уравнения , удовлетворяющее начальному условию .
Решение. Очевидно, что для данного уравнения на всей плоскости выполнены условия теоремы существования и единственности решения задачи Коши. Строим последовательность функций, определяемых соотношениями (3), приняв за нулевое приближение :
Ясно, что при . Непосредственной проверкой убеждаемся, что функция решает поставленную задачу Коши.
Пример 2. Методом последовательных приближений найти приближенное решение уравнения , удовлетворяющее начальному условию в прямоугольнике
Решение. Имеем , т. е. . За берем меньшее из чисел , т. е. . Последовательные приближения согласно (4) будут сходится в интервале . Составляем их
Абсолютная погрешность третьего приближения не превосходит величины
Замечание. Функция должна удовлетворять всем условиям теоремы существования и единственности решения задачи Коши.
Следующий пример показывает, что одной непрерывности функции недостаточно для сходимости последовательных приближений.
Пусть функция определена следующим образом:
На множестве , функция непрерывна и ограничена постоянной . Для начальной точки последовательные приближения при имеют вид:
Поэтому последовательность для каждого не имеет, предела, т. е. последовательные приближения не сходятся. Заметим также, что ни одна из сходящихся подпоследовательностей и не сходится к решению, поскольку
Если же последовательные приближения сходятся, то полученное решение может оказаться неединственным , как показывает следующий пример: .
Возьмем начальное условие ; тогда
Беря в качестве нулевого приближения функцию , будем иметь
так что все последовательные приближения равны нулю и поэтому они сходятся к функции, тождественно равной нулю. С другой стороны, функция представляет собой также решение этой задачи, существующее на полупрямой .
метод последовательных приближений
М етод последовательных приближений (или метод Пикара) является аналитическим, т. е. позволяет получить приближённое решение задачи Коши, определяемой дифференциальным уравнением (1) с начальным условием (2), в виде формулы. Возник метод в связи с доказательством теоремысуществования и единственности решения задачи Коши (гл. 1).
Пусть в условиях данной теоремы требуется найти решение уравнения (1) с начальным условием (2). Проинтегрируем обе части уравнения (1) от х0 доx:
, откуда
у(х) = у0 + 
. (7)
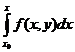
Очевидно, что решение интегрального уравнения (7) будет удовлетворять уравнению (1) и начальному условию (2). Действительно, при х =х0 получим
у(х0) = у0 +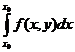 
= у0.
Применим к интегральному уравнению (7) метод последовательных приближений. Заменим в равенстве (7) неизвестную функцию у данным значением у0, получим первое приближение
у1(х) = у0 + 
.
Заметим, что интеграл в правой части содержит только одну переменную х, поэтому аналитическое выражение первого приближения у1(х) будет являться функцией, зависящей
от х.Заменим теперь в равенстве (7) неизвестную функцию у найденным значением у1(х), получим второе приближение
у2(х) = у0 + 
и т. д. В общем случае итерационная формула имеет вид
уn(х) = у0 + 
( n =1, 2, . ). (8)
Применив неоднократно формулу (8), получим последовательность функций
Можно доказать [1, 2, 3], что эта последовательность сходится и
= у(х),
т.е. предел последовательности является решением интегрального уравнения (7), а следовательно, и дифференциального уравнения (1) с начальным условием (2). Это означает, что k-й член последовательности (9) является приближением к точному решению уравнения (1)
с определённой степенью точности.
Погрешность k-го приближения можно оценить формулой
, (10)
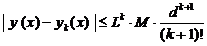
где L — постоянная Липшица; М — верхняя грань модуля функции f, т.е.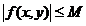 
;
величина d для определения окрестности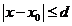 
вычисляется по формуле 
, числаа и b— из неравенства Липшица (гл. 1).
Пример 1. Найти три последовательных приближения решения дифференциального уравнения у’ = x + y 2 ,удовлетворяющего начальному условию у(0) = 1.
Решение.В качестве начального приближения возьмём
первое приближение у1(х) = у0 + = 1+ 
,
второе приближение у2(х) = у0 + 
= 1+ 
,
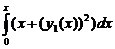
третье приближение у3(х) = у0 + 
= 1+ 
.
Вычисления интегралов и построение графиков полученных функций у1(х), у2(х), у3(х) проведём в системе MathCAD. Результаты решения представлены на рис. 14.
Оценим погрешность третьего приближения.
Для определения области G, заданной неравенствами (6), примема = 1, b = 2. Получим
G: – 1 
х 1,–1 y 3.
В прямоугольнике G функция
определена и непрерывна, причём: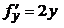 
,
,
,
= 
.
По формуле (10) получим
.
 |
Рис. 14
Заметим, что в программе MathCAD для вычисления интегралов с переменным верхним пределом интегрирования, необходимо выполнить следующие действия:
1) записать интеграл и выделить его в рамку;
2) выбрать команду Evaluate (Вычислить) из меню опции Simbolic (Символика) главного меню.
Существует и другой способ вычисления несобственных интегралов в программе MathCAD, по которому следует:
1) записать интеграл и выделить его в рамку;
2) выбрать команду Simplify (Упростить) из меню опции Simbolic (Символика) главного меню.
Пример 2. Найти пять последовательных приближений решения дифференциального уравнения
удовлетворяющего начальному условию у(0) = 0.
Сравнить полученные приближения с точным решением.
Решение.В качестве начального приближения возьмём
Решение данного уравнения, проведённое в системе MathCAD, показано на рис. 15.
 |
Рис. 15
МетодЭйлера
М етод Эйлера относится одновременно к численным и к графическим методам решения дифференциальных уравнений.
Суть метода заключается в том, что искомую интегральную кривую y = y(x) заменяют ломаной M0M1M2 . звенья которой являются касательными к интегральным кривым (рис. 16).
Рис. 16
Пусть требуется решить задачу Коши, т.е. найти решение дифференциального уравнения (1) с начальным условием (2) в виде функции y = y(x). Выбрав шаг h, построим, начиная
с точки х0, систему равноотстоящих точек:
Вместо искомой интегральной кривойy = y(x) на отрезке [х0, х1]рассмотрим отрезок касательной L1 к ней в точке М0 (х0, y0). Уравнение касательной L1, в силу (1), имеет вид
При х = х1 из уравнения касательной L1 получим
откуда видим, что приращение функции на первом шаге имеет вид
у0 = hf(х0, y0).
Аналогично, проводя касательную L2 к некоторой интегральной кривой семейства в точке М1(х1, y1), получим
у1= hf(х1, y1).
Таким образом, значения искомой функции y(x) могут быть определены по формулам:
yi+1 =yi + у i, у i = hf(х i, yi), (11)
где i= 0,1,2, . , которые называются вычислительными формулами метода Эйлера.
При этом искомую интегральную кривую y = y(x), проходящую через точку М0 (х0, y0), приближённо заменяем так называемой ломаной ЭйлераM0M1M2 . звенья которой MiMi+1 прямолинейны между прямыми x = xi, x = xi+1 и имеют подъём
.
Метод Эйлера является простейшим численным методом, удобным в применении, однако он имеет ряд существенных недостатков. Основной из них — малая точность. Она равна порядку h 2 , причём с каждым шагом погрешность возрастает, т.е. происходит систематическое накопление ошибок. Поэтому на практике часто используют способ двойного счёта — с шагом hи с шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах даёт естественные основания считать их верными.
Пример.
1. Найти методом Эйлера численное решение дифференциального уравнения
у’ = x 3 + y,удовлетворяющее начальному условию у (0) = 1, на отрезке [0, 1] с шагом h = 0,1.
2. Найти точное решение уравнения у’ = x 3 + y и сравнить его с приближённым на отрезке [0, 1].
1. Для данного уравнения вычислительные формулы (11) имеют вид:
yi+1 =yi + у i, у i = 0,1(х i 3 + yi),
Учитывая, что погрешность метода имеет порядок h 2 = 0,01, достаточно в промежуточных результатах брать три цифры после запятой, а во всех yiсохранять только две цифры.
Результаты вычислений оформим в виде таблицы.
| i | х i | yi | yi = hf( х i , yi) = 0,1( х i 3 + yi) |
| 0 | 0 | 1 | 0,1 |
| 1 | 0,1 | 1,1 | 0,110 |
| 2 | 0,2 | 1,21 | 0,122 |
| 3 | 0,3 | 1,33 | 0,136 |
| 4 | 0,4 | 1,47 | 1,634 |
| 5 | 0,5 | 1,62 | 0,175 |
| 6 | 0,6 | 1,79 | 0,201 |
| 7 | 0,7 | 1,99 | 0,233 |
| 8 | 0,8 | 2,22 | 0,273 |
| 9 | 0,9 | 2,49 | 0,322 |
| 10 | 1 | 2,82 | — |
2. Данное уравнение у’ = x 3 + y является линейным дифференциальным уравнением первого порядка. Решим его методом Бернулли.
Полагая y = uv, имеем
= 0.
Сгруппируем члены, содержащие uв первой степени, получим
= 0.
Полагаем 
= 0, откуда 
. Интегрируя, находим 
, или 
(постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).
Для нахождения uимеем уравнение
,
.
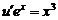
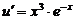
Разделим переменные, получим 
, откуда
.
Интегрируем по частям три раза:
.
Таким образом, общее решение данного уравнения
y = uv =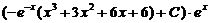 
,
или y = 
.
Используя начальное условие у (0) = 1, получим 1 = ‑ 6 + С, откуда С = 7. Следовательно, искомое частное (точное) решение имеет вид
у = 
.
Вычислим значения полученного точного решения на отрезке [0, 1] с шагом h = 0,1. Результаты округлим до 0,01 и запишем в таблицу.
| i | х i | Приближённые значения yi | Точные значения y (х i ) |
| 0 | 0 | 1 | 1 |
| 1 | 0,1 | 1,1 | 1,11 |
| 2 | 0,2 | 1,21 | 1,22 |
| 3 | 0,3 | 1,33 | 1,35 |
| 4 | 0,4 | 1,47 | 1,5 |
| 5 | 0,5 | 1,62 | 1,67 |
| 6 | 0,6 | 1,79 | 1,86 |
| 7 | 0,7 | 1,99 | 2,08 |
| 8 | 0,8 | 2,22 | 2,35 |
| 9 | 0,9 | 2,49 | 2,66 |
| 10 | 1 | 2,82 | 3,03 |
Сравнение приближённого (численного) решения данного дифференциального уравнения с точным на промежутке [0, 1] проведём с помощью системы MathCAD.
Результаты сравнения, а также численное решение данного уравнения, проведённое методом Эйлера в системе MathCAD, представлены на рис. 17.
 |
Рис. 17
МодификацииметодаЭйлера
Существуют различные уточнения метода Эйлера, повышающие его точность. Цель модификаций — более точно определить направление перехода из точки (х i, yi) в точку (х i +1, yi +1). Так, метод Эйлера-Коши предлагает вычислять значения искомой функции y(x) по формулам:
= yi + Ду i, Ду i = hf(х i, yi),
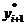
yi+1 = yi + h 
,i= 0,1,2, . .
Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке (х i, yi) и во вспомогательной точке (х i +1, 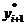). В качестве окончательного берём среднее этих направлений.
Другой модификацией метода Эйлера является усовершенствованный метод ломаных, при котором сначала вычисляют промежуточные значения:
, 
и находят значение направления поля интегральных кривых в средней точке (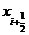 
, 
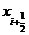
), т.е. 
= f( , ), а затем полагают
yi+1 = yi + h .
Метод Эйлера и его модификации являются простейшими представителями конечно-разностных методов (шаговых методов) для приближённого решения задачи Коши.
Поскольку описанные методы предполагают повторяющиеся вычисления на каждом шаге, то они легко программируются и могут быть реализованы на компьютере.
На рис. 18 и 19 показаны решения дифференциального уравнения у’ = x 3 + y,удовлетворяющего начальному условию у(0) = 1, полученные модифицированными методами Эйлера (методом Эйлера-Коши и усовершенствованным методом ломаных) с помощью системы MathCAD.
 |
Рис. 18
 |
Рис. 19
Метод Рунге-Кутта
Рассмотренный выше метод Эйлера относится к семейству методов Рунге-Кутта и является их простейшим частным случаем (методом первого порядка точности). Наиболее известным из методов Рунге-Кутта является классический четырёхэтапный метод четвёртого порядка точности. Его расчётные формулы для решения задачи Коши, определённой уравнениями (1) и (2), имеют вид:
yi+1 =yi + у i; у i= 
( k1 (i) + 2k2 (i) + 2k3 (i) + k4 (i) ), (12)
k2 (i) = h f (х i + 
,yi + 
);
k3 (i) = h f (х i + , yi + 
);
Погрешность метода на каждом шаге является величиной порядка h 5 .
Геометрический смысл использования метода Рунге-Кутта с вычислительными формулами (12) состоит в следующем (рис. 20).
 |
Рис. 20
Из начальной точки М0(х0, y0) сдвигаются в направлении, определяемом углом 
1, для которого tg 1= f (х0, y0). Идут в этом направлении на полшага, т.е. до вертикальной прямой
х = х0 + 
. На этом направлении выбирается точка Р1с координатами
Затем из точки М0(х0, y0)сдвигаются в направлении, определяемом углом 2, для которого tg 2 = f (х0 + ,y0 + 
), и на этом направлении выбирается точка Р2с координатами
.
Далее из точки М0(х0, y0) сдвигаются в направлении, определяемом углом 3, для которого tg 3 = f . На этом направлении выбирается точка Р3с координатами
(х0 + h, y0 + k3 (0) ). Этим задаётся ещё одно направление, определяемое углом 4, для которого tg 4 = = f(х0 + h, y0 + k3 (0) ). Четыре полученных направления усредняются в соответствии с формулой
= 
(k1 (0) +2k2 (0) + 2k3 (0) + k4 (0) ).
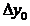
На этом окончательном направлении и выбирается очередная точка М1с координатами (х1, y1) = (х0+ h, y0 + 
).
Теперь, уже исходя из точки М1, все построения с помощью усреднений направлений повторяют сначала. Идут в новом усреднённом направлении до вертикальной прямой х = х2, получают точку М2(х2, y2) и т.д.
Эффективная оценка метода Рунге-Кутта затруднительна [2, 4]. Поэтому для определения правильности выбора шага h на практике обычно на каждом этапе из двух шагов применяют двойной пересчёт, а именно: исходя из текущего верного значения y(х i) вычисляют величину y(х i+ 2h) двумя способами: один раз с шагом h, другой раз — с двойным шагом 2h .
Если расхождение полученных значений не превышает допустимой погрешности, то шаг hдля данного этапа выбран правильно и полученное с его помощью значение можно принять за y (х i+ 2h). В противном случае шаг уменьшают в два раза.
На практике при вычислениях по формулам (15) обычно пользуются схемой, приведённой в таблице.
| i | x | Y | k = hf (х, y ) | у |
| 0 | х 0 х0 +  х0 + х0 + h | y 0 y0 +  y0 +  y0 + k3 (0) | k1 (0) k2 (0) k3 (0) k4 (0) | k1 (0) 2k2 (0) 2k3 (0) k4 (0) |
| — | — | — | — |  |
| 1 | х1 | y1 | . . . | . . . |
Пример. Найти методом Рунге-Кутта решение дифференциального уравнения у’ = x 3 + y,удовлетворяющего начальному условию у(0) = 1, на отрезке [0, 1] с шагом h = 0,1.
Решение.Учитывая, что погрешность метода имеет порядок h 5 = 0,00001, в промежуточных результатах следует брать пять цифр после запятой, а во всех yiсохранять только четыре цифры. Результаты вычислений оформим в виде таблицы.
| i | х | y | k = 0,1(х 3 + y ) | y |
| 0 | 0 0,05 0,05 0,1 | 1 1,05 1,0525 1,1053 | 0,1 1,10501 1,10526 1,11063 | 0,1 0,21003 0,21053 0,11063 |
| 0,1052 | ||||
| 1 | 0,1 0,15 0,15 0,2 | 1,1052 1,1604 1,1634 1,2219 | 0,11062 0,11637 0,11668 0,11136 | 0,11062 0,23278 0,21121 0,11136 |
| 0,10556 | ||||
| 2 | 0,2 0,25 0,25 0,3 | 1,2218 1,2717 1,2752 1,3399 | 0,12188 0,12874 0,12908 0,13669 | 0,12188 0,25747 0,25816 0,13669 |
| 0,12903 | ||||
| 3 | 0,3 0,35 0,35 0,4 | 1,3520 1,4081 1,4124 1,4853 | 0,13668 0,1451 0,14552 0,15493 | 0,13668 0,2902 0,29105 0,15493 |
| 0,14548 | ||||
| 4 | 0,4 0,45 0,45 0,5 | 1,4988 1,5628 1,568 1,6512 | 0,15493 0,16539 0,16591 0,17762 | 0,15493 0,33078 0,33182 0,17762 |
| 0,16586 | ||||
| 5 | 0,5 0,55 0,55 0,6 | 1,6661 1,74 1,7465 1,8425 | 0,17762 0,19064 0,19132 0,20585 | 0,17762 0,38128 0,38258 0,20585 |
| 0,19122 | ||||
| 6 | 0,6 0,65 0,65 0,7 | 1,8588 1,9618 1,9699 2,0826 | 0,20584 0,22199 0,2228 0,24082 | 0,20584 0,44399 0,4456 0,24082 |
| 0,22271 | ||||
| 7 | 0,7 0,75 0,75 0,8 | 2,0833 2,1855 2,1955 2,3268 | 0,24081 0,26074 0,26173 0,28388 | 0,24081 0,52148 0,52347 0,28388 |
| 0,26161 | ||||
| 8 | 0,8 0,85 0,85 0,9 | 2,3468 2,4898 2,5021 2,6585 | 0,28589 0,3104 0,31162 0,33875 | 0,28589 0,62079 0,62324 0,33875 |
| 0,31145 | ||||
| 9 | 0,9 0,95 0,95 1 | 2,6582 2,8545 2,8695 3,0566 | 0,34129 0,37119 0,37269 0,40566 | 0,34129 0,74238 0,74537 0,40566 |
| 0,37245 | ||||
| 10 | 1 | 3,0280 |
Соответствующее решение данного дифференциального уравнения, полученное методом Рунге-Кутта в системе MathCAD, представлено на рис. 21.
 |
Рис. 21
Лабораторная работа
«Численные методы решения задачи Коши
для обыкновенных дифференциальных уравнений»
Задание 1.
1. Для заданного дифференциального уравнения первого порядка у’ = f(x , y) c начальным условием у (a) = c найти приближённое решение в виде многочлена пятой степени.
2. Найти численное решение данного дифференциального уравнения на отрезке [a, b] с шагом интегрирования h, округляя результат до 0,001.
3. Найти точное решение заданного дифференциального уравнения у’ = f (x, y) и сравнить его с приближённым на отрезке [a, b]. Построить графики полученных решений.
Исходные данные для 15-ти вариантов содержатся в таблице.
| Вариант | f ( x , y ) | a | b | с | h |
| 1 |  | 0 | 1 | 0 | 0,1 |
| 2 |  | 0 | 1 | 1 | 0,1 |
| 3 |  | 0 | 2 | 0 | 0,1 |
| 4 |  | p | 2p | 0 | p/10 |
| 5 |  | 1 | 2 | 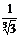 | 0,1 |
| 6 |  | 1 | 3 | 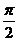 | 0,2 |
| 7 | 4 +  | 1 | 2 | 2 | 0,1 |
| 8 |  | 1 | 2 | 0 | 0,2 |
| 9 |  | 0 | 2 | 0 | 0,1 |
| 10 |  | 0 | 2 | 1 | 0,2 |
| 11 |  | 1 | 2 | 0 | 0,2 |
| 12 | –  | 0 | 1 | p/4 | 0,1 |
| 13 | –  |  |  | е | 0,1 |
| 14 |  | 0 | 1 | 1 | 0,1 |
| 15 |  | 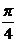 | 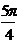 | 0 | 0,3 |
Указания к выполнению задания 1
1. Для того, чтобы получить приближённое решение заданного дифференциального уравнения в виде многочлена пятой степени, используйте формулу (3) при k = 0, 1, . 5.
2. При выборе метода для вычисления точного решения учитывайте то, что дифференциальные уравнения вариантов 1- 4 являются линейными дифференциальными уравнениями, уравнение 5-го варианта — уравнение Бернулли, уравнения 6-8-х вариантов — однородные дифференциальные уравнения, а уравнения 9-15-х го вариантов — дифференциальные уравнения с разделяющимися переменными.
3. Для сравнения точного и приближённого решений заданного дифференциального уравнения сначала составьте таблицы их значений на отрезке [a , b], затем постройте на этом же отрезке графики полученных решений.
Задание 2. Решить задачу Коши для обыкновенного дифференциального уравнения первого порядка у’ = f(x , y) на отрезке [a , b]при заданном начальном условии у(a) = c и шаге интегрирования h:
1) методом Эйлера с шагом 2h и с шагомh;
2) модифицированным методом Эйлера (методом Эйлера — Коши или усовершенствованным методом ломаных);
3) методом Рунге-Кутта с шагом 2h и с шагомh.
Результаты округлить до 0,0001. Сравнить полученные разными методами решения. Построить графики полученных решений.
Метод последовательных приближений
Метод последовательных приближений
- Интегрирование нелинейных дифференциальных уравнений вынужденных колебаний может быть выполнено с использованием метода аппроксимации последовательного приближения. Большое количество экспериментов и наблюдений за работой оборудования, выполняющего нелинейные вынужденные колебания, свидетельствуют о наличии периодических движений в установившемся состоянии. Поэтому, применяя метод последовательного приближения, получаем периодическое решение круговой частоты, равной круговой частоте возмущенной силы. Поясним идею этого метода на примере дифференциального уравнения Я к Х ПФ х 4-ч греха пт. Здесь p. и w-малый параметр, f x -непрерывная нелинейная нечетная функция x.
В качестве начального приближения опустите нелинейное частное pf x этого уравнения, чтобы найти конкретное решение xa соответствующего линейного дифференциального уравнения. Д Л Х1 L81pr. Легко увидеть решение х а sinpi Удовлетворяют этому уравнению. Затем назначьте полученное значение xt нелинейной функции p x , чтобы найти 2-е приближение x .То есть мы вычисляем дифференциальное уравнение, а затем интегрируем его. Н2 А ХД ПФ х, ч греха пт. После решения этого уравнения определите 2-е приближение Си Б2 греха пт БС грех 3 ПТ В8 грех 5пт — -… если мы введем xa в нелинейную функцию p x , то есть вычислим p xa , то найдем 3-е приближение xa. Вы можете получить его, интегрируя уравнения.
Гак как материальная система состоит из конуса и двух грузов, то момент инерции системы равен сумме моментов инерции конуса и грузов. Людмила Фирмаль
Определяются и последующие приближения. Ниже приведена последовательность, которая решает задачу с вынужденными колебаниями в нелинейных системах с использованием слегка модифицированного метода Даффинга. она основана на методе последовательного приближения. О. Дуффинга, Erzwungene СЧ Wingen беи veranderlicher Eigenfrequenz УНД jhaltechne BedeQtung, Брауншвейг 1918. 1 Создать дифференциальное уравнение для вынужденных колебаний нелинейной системы Х к Х х фут греха пт gvl p и ft-малые параметры, а f x — непрерывная нелинейная функция, x.
Здесь мы рассмотрим случай, когда x -нечетная функция, т. е. — x — x , а проекция возмущенной силы-ft sin p. 2 Определите первое приближение xx. предположим q 0.То есть интегрируем линейное уравнение X A x ftsinpf. когда xf принимает личное решение Х1 a1sinpf Здесь коэффициент ah подлежит последующему определению. 3 Добавить термин p X в левую и правую части уравнения в пункте 1 и записать его в следующем формате Х р2х П — А х р х фут греха пт -. 4 чтобы определить 2-е приближение x2, вставьте значение x1 a1sinp P. 2 p.
В правую часть уравнения, т. е. Х п х па-АА Си является cxi обладает фут греха пт 5 использовать простейшее выражение для выражения нечетной функции Xi f in sin pt в виде тригонометрического ряда 2 isin pZ. In другими словами, xj A. sin p , где 1, 3, 5 6 ввести этот результат в дифференциальное уравнение пункта 4 и представить в виде Х х п р -а а — -в формате pxi фут грех Пи щ х, грех ИПТ Где 1 3, 5,…
В связи с нахождением периодического решения этого уравнения возьмем коэффициент, равный нулю в sin pt и решим уравнение p1-Aa aj plj — — ft 0 для определения значения ai p2-A8 ax Ai 0-0 равно 1 от удельного решения производной Уравнение в предыдущем абзаце бесконечно увеличивается в соответствии с законом — a 1 1- — в T cos pt искомое решение является апериодическим 8 при условии p -Aa ax pL1 — — A 0 отличается Пункт 6 социальные уравнения принимают вид −5 Р2х p2M1p ПЛ Здесь. 1 3 5 7…Интегрируем это уравнение и находим 2-е приближение х, ВХ греха пт БС грех 3 ПТ В6 5пф…
Где первый член bx sin pt является общим решением соответствующего однородного уравнения p2×0, а все остальные члены являются частными решениями этого неоднородного уравнения. 9 после дуффинга, коэффициенты B и A коэффициентов 2-го приближения первой пункт 2 и пункт 8 греха Пи сделать постоянный эквивалент. дя грех п БС греха 3 РФ бб грех 5П Здесь ai определяется в 7. 10 xt-определяет 3-е и последующие приближения в соответствии с набором вычислений, описанных в п. 4 −9. Метод непрерывной аппроксимации дуффинга является одним из наиболее распространенных методов аппроксимации для интегрирования нелинейных дифференциальных уравнений вынужденных колебаний.
Если вы хотите определить только первое приближенное значение jcx alsin rf, то вам нужно составить дифференциальное уравнение 2-го приближенного значения и приравнять коэффициент stnpt к нулю см. Раздел 7, затем вычислить амплитуду av. Тогда 2-е приближение не вычисляется с большими усилиями см. 8 и 9. Заметим, что если перейти от 2-го приближения к 3-му особенно ко всем последующим, то объем вычислений резко возрастет, а точность результата увеличится незначительно. Поэтому она обычно ограничивается определением 2-го приближения.
Задача 20.8. Найти периодический закон вынужденных колебаний точки масс m, которая движется вдоль оси x под действием нелинейной упругой силы F и возмущающей силы S с жесткими свойствами. Проекция этих сил на ось x равна Hx — ctx-ctx , SX H sin pt. Где ct ct и H-положительные постоянные коэффициенты, а c и H-малые параметры. Эта задача решается методом последовательных дуффинговых приближений, который описан в обзоре теории. Найдите первое и второе приближения. Решение. Дифференциальное уравнение массовой точки mX Fx Sx после подстановки значений Fx и 5X принимает вид mx — ctx-cp Wsinpf, то есть Джей — к Х-Х — УГ ДНР, 1 Где k Ди м, ф квю, ч — ч м.
Заметим, что, как и c и H, коэффициенты y и ft являются малыми параметрами, y 0 и u 0. При определении первого приближения xx будем считать, что y 0 в уравнении 1.Линейные дифференциальные уравнения — k x — hs. легко видеть, что npt удовлетворяет решению. ХХ axslnpf, 2 Где ah-константа, которая будет определена позже. Используйте уравнение 1 в качестве первого приближения к нелинейному дифференциальному уравнению 2. Перейти ко 2-му приближению definition.
- To для этого добавьте термины слева и справа от выражения 1 Х х п -Аи х-1 х ftsinpf. Расчет 2-го приближения сводится к интегрированию дифференциальных уравнений 3.Справа от него 1-е приближение 2 заменяется на x. Х р х АИ п -А2 грех пт — СЛН ПФ ФТ греха пт для СЛН ПРОМАЛЬП 3 греха пт-грех 3 ПТ, представьте себе это Уравнение формы л р х Асин РФ г yafsin 3 ПТ, 4 Где это показано Поскольку термин AsinpA включен в правую часть, легко видеть, что случай резонанса соответствует дифференциальному уравнению 4.фактически, 1 из этого частного решения является x — icos rt, бесконечно увеличивающимся с течением времени. Условия определяют периодический закон движения points.
В правой части Формулы 4 термина Asin rf не существует, то есть коэффициент A должен быть равен нулю. Используя формулу 5, Р −4, −4×4 −0. Уравнение 6 позволяет определить величину амплитуды амплитуды амплитуды а в первом приближении в зависимости от круговой частоты Р возмущающей силы. Графический метод решения этого уравнения показан ниже. При выполнении условия 6 дифференциальное уравнение 4 принимает вид р х йадж греха 3 л 7 Общим решением xi уравнения 2, которое является желательным 2-м приближением, является формула J X2 X2, 8 Где xi1 — решение соответствующего однородного уравнения, а x — конкретное решение уравнения 7.
На боковой поверхности кругового конуса симметрично расположены два груза, соединенные между собой тонкой нитью и отстоящие от оси вращения конуса па расстоянии одной трети радиуса основания конуса. Людмила Фирмаль
Это легко увидеть. x i bxsinpt Является 1 из решения однородного уравнения X p x 0.Параметр bx определен ниже. Следуйте правой части выражения 7, чтобы найти конкретное решение x G в виде ХВ Дсин 3 ПТ. 10 Подставляя функцию 10 и ее вторую производную Xi — 9Dp2sin3pZ в уравнение 7, находим D -уа 32р2 и вводим значение этого D в конкретное решение 10. 8 из 9 и II получить 2-е приближение, используя результат. x, b1sinp — fSin3pt 12 После дуффинга, мы сделаем коэффициентов AX и BX равны.
Они находятся в sinptf в первом 2 и втором 12 приближениях. Тогда мы, наконец, получаем 2-е приближение искомого периодического движения. ХГ грех пт-грех 3 пт 13 Если мы сравним 1-е 2 и 2-е 13 приближения, то увидим, что их разность xt-Xi имеет порядковую величину малость параметра y. — 3 ПТ СЛН. В заключение рассмотрим графическое решение уравнения 6 для определения зависимости возмущающей силы амплитуды а первого приближения от круговой частоты р. Отметим формулу 6. Таким образом, определенный диапазон значений p соответствует 3 значениям ax. Левая и правая части уравнения 14 представлены y 15.
Рисунок отображаются Декартовые оси, значения ab отображаются на горизонтальной оси, а значения y отображаются на вертикальной оси. Функция y pat соответствует независимой параболе 3-го порядка. В какой-то момент см. рисунок а. И затем… значение p k. Функция j jp-4-l Oi соответствует пучку линий, проходящих через точку. Линия, равная −1, зависит от соотношения круговой частоты p k возмущающей силы и свободного колебания.
Так, величина p A 0 соответствует прямой линии a-a, угловой коэффициент соответствует минус 1, величина p k 1 соответствует прямой линии 0-0, а угловой коэффициент соответствует 0.Значение Л оо-прямая линия, совмещенная с осью Y, угловой коэффициент равен infinity. So, если p k непрерывно изменяется от нуля до бесконечности, прямая a — a вращается против часовой стрелки до тех пор, пока не совпадет с осью Y. если p k O, то линия a-a пересекает параболу с определенным значением p k, линия Нажмите одну ветвь параболы и перейдем на другую ветку. если p k еще больше увеличить, а затем повернуть линию, то линия пересечет параболу в 3 точках.
Абсцисса пересечения прямой и параболы фиксирует искомое значение dp. В дальнейшем это называется амплитудой нелинейных вынужденных колебаний. Это название условно, но вполне оправдано тем, что в Формуле 13 оно является a, yaf 32 fact. Рисунок Б построение кривой f p k. как видно, не 1 амплитуда av, а 3 соответствует определенному диапазону p k Values. In сравнение с соответствующим графиком линейной упругой силы см. Рис. 2 на стр. 111 в томе 8.14, амплитудная кривая стр. 373 см. кривую — на рис. 20.1, остается прерывистой и наклоняется в сторону увеличения p k отметка абсциссы на рис. b соответствует резонансу, вызванному линейной упругой силой.
Если решить соответствующую задачу с учетом сопротивления, пропорционального скорости, то кривая будет непрерывной см. пунктирную кривую на рисунке Ff. в этом случае при увеличении сопротивления площадь 3 амплитуд уменьшается. Аналогичный шаг будет обсужден позже в выпуске 20.9. Если решить эту задачу в случае мягких свойств силы упругости см. рис. 373 на стр. 20.1, кривые 2-2, то есть, если — c x CiX , где Ci 0 и cs 0, амплитудная кривая см. Рисунок c наклоняется в сторону уменьшения p k.
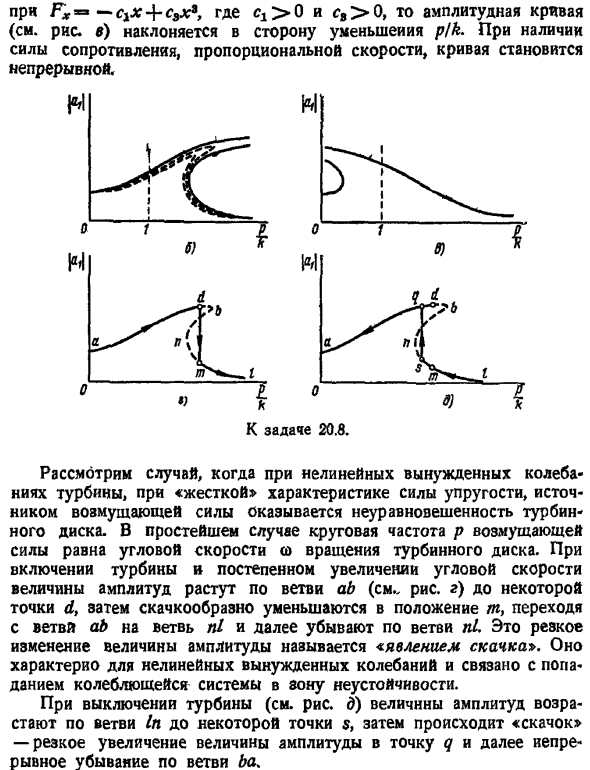
Если существует сопротивление, пропорциональное скорости, кривая Рассмотрим случай, когда диск турбины несбалансирован из-за жесткости, характерной для упругой силы, которая является источником возмущающей силы, при нелинейном вынужденном колебании turbine. In в простейшем случае круговая частота P возмущающей силы равна угловой скорости вращения W диска турбины. При включении турбины и постепенном увеличении угловой скорости амплитуда увеличивается вдоль ветви ab см. Рисунок D до некоторой точки d, затем резко уменьшается до положения m, затем переходит от ветви ab к ветви nl и уменьшается вдоль ветви l .Внезапное изменение величины этой амплитуды называется феноменом скачка.
Это характерно для нелинейных вынужденных колебаний, которые связаны с колебательными системами, попадающими в неустойчивую систему. Когда турбина выключена см. Рисунок е, амплитуда увеличивается вдоль ветви in до определенной точки s и происходит скачок.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://lektsii.org/18-75255.html
http://lfirmal.com/metod-posledovatelnyh-priblizhenij/