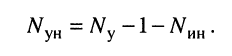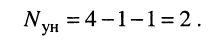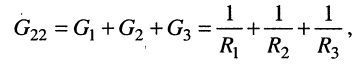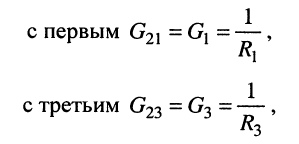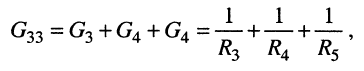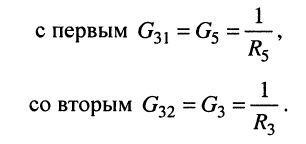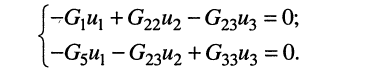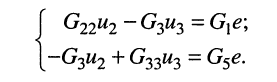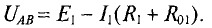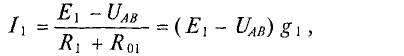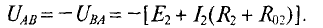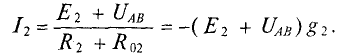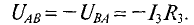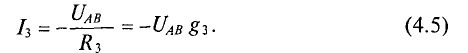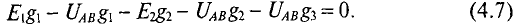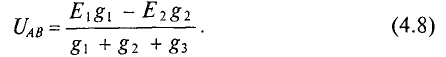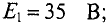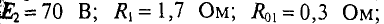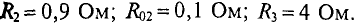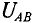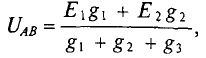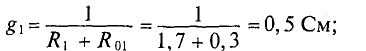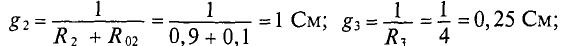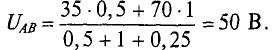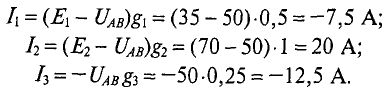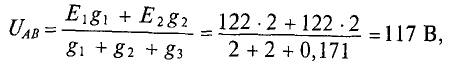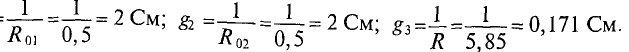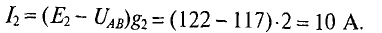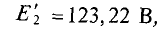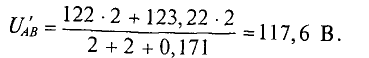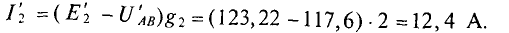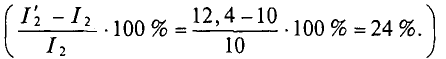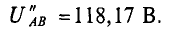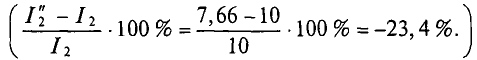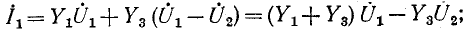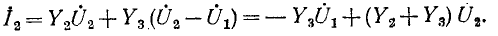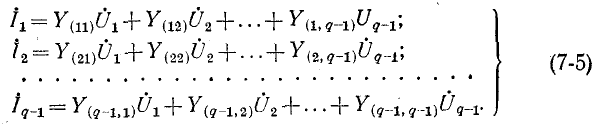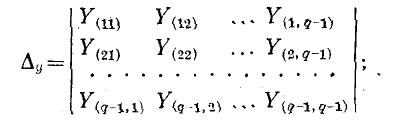Метод узловых (потенциалов) напряжений
При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.
Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие.
В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.
Метод узловых потенциалов примеры решения задач
Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.




Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.
Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.
В общем виде система имеет вид:
Использованные в этой системе уравнений буквенно-цифровые обозначения
имеют следующий смысл:





Аналогично находятся и остальные проводимости:
J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае
В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:
Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:
В результате получены следующие значения потенциалов в узлах цепи:
Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.
В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что
Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.
Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.
Транспортная задача — решение методом потенциалов
Одна из самых распространенных и востребованных оптимизационных задач в логистике — транспортная задача. В классическом виде она предполагает нахождение оптимального (т. е. сопряженного с минимальными затратами) плана грузоперевозок.
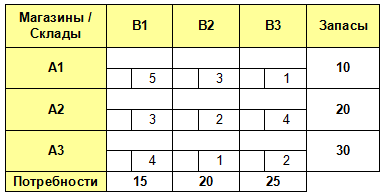
Например, у нас есть сеть розничных магазинов, которым требуется определенное количество товаров. Также имеется ряд складов поставщиков, где требуемые товары хранятся. При этом на каждом складе различный объем запасов этих товаров. Кроме этого нам известны тарифы — затраты на перевозку 1 товара от каждого склада к каждому магазину.
Возникает необходимость разработать такой план перевозок, чтобы магазины получили требуемое количество товаров с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.
Теоретический материал по транспортной задаче
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.
Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.
Математическая модель транспортной задачи имеет следующий вид:
где: Z — затраты на перевозку грузов;
X — объем груза;
C — стоимость (тариф) перевозки единицы груза;
A — запас поставщика;
B — запрос потребителя;
m — число поставщиков;
n — число потребителей.
Общий план решения транспортной задачи методом потенциалов
Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов . Один из наиболее применяемых и подходящих для большинства случаев методов — итерационное улучшение плана перевозок.
Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален — решение найдено. Если нет — улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.
Ниже приведен алгоритм решения транспортной задачи в самом общем виде:
- Построение транспортной таблицы.
- Проверка задачи на закрытость.
- Составление опорного плана.
- Проверка опорного плана на вырожденность.
- Вычисление потенциалов для плана перевозки.
- Проверка опорного плана на оптимальность.
- Перераспределение поставок.
- Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.
- Вычисление общих затрат на перевозку груза.
- Построение графа перевозок.
Подробная инструкция по решению транспортной задачи
1. Построение транспортной таблицы
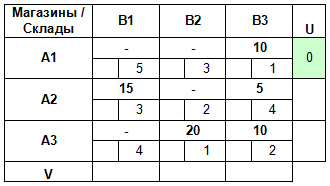
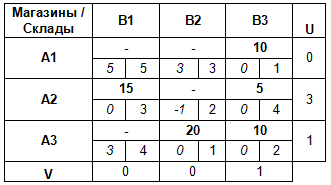
Заполняем транспортную таблицу с исходными данными, где указываем запасы материалов, имеющиеся на складах поставщиков (Ai), и потребности заводов (Bj) в этих материалах.
В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (Cij).
2. Проверка задачи на закрытость
Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей — символом B.
Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.
Проверим задачу на закрытость:
A = 10 + 20 + 30 = 60.
B = 15 + 20 + 25 = 60.
A = B, следовательно данная транспортная задача — закрытая.
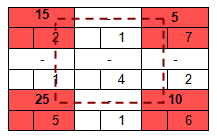
3. Составление опорного плана
Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик» или «набросок», итерационно улучшая который мы постепенно придем к оптимальному плану.
Есть разные методы нахождения опорного плана. Наиболее распространены следующие:
Суть метода проста — ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении сверху вниз и слева направо. То есть сперва заполняется самая верхняя левая ячейка («северо-западная» ячейка), потом следующая справа и т. д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.
Подробное описание метода и пример можно посмотреть здесь.
Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным тарифом. Затем выбирается следующая клетка с наименьшим значением тарифа и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).
Подробное описание метода и пример можно посмотреть здесь
Основа метода в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшей разностью заполняется клетка с наименьшим тарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.
Подробное описание аппроксимации Фогеля и пример можно посмотреть здесь
Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.
Подробное описание метода и пример можно посмотреть здесь
Выберите один из методов и пройдите по ссылке в его описании, чтобы посмотреть как в данном примере был составлен опорный план и заполнена транспортная таблица.
4. Проверка опорного плана на вырожденность
Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.
План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n — 1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся).
Проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!
План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:
Ломаная линия может иметь точки самопересечения, но не в клетках цикла.
В нашем примере количество базисных клеток = 5; m + n — 1 = 3 + 3 — 1 = 5.
Следовательно, первоначальный план перевозок — невырожденный (5 = 5).
5. Вычисление потенциалов для плана перевозки
Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.
Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.
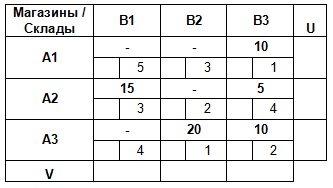
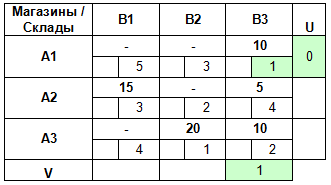
Итак, сопоставим каждому поставщику Ai и каждому потребителю Bj соответствующие величины Ui и Vj так, чтобы для всех базисных клеток плана было выполнено следующее соотношение: Ui + Vj = Cij.
Добавим к транспортной таблице дополнительную строку и столбец для Ui и Vj.
Предположим, что U1 = 0.
Тогда мы сможем найти V3 = C13 — U1 = 1 — 0 = 1.
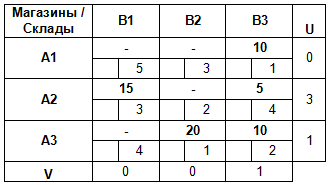
Зная V3, мы теперь можем найти U3:
По аналогии вычисляем все оставшиеся потенциалы:
6. Проверка плана на оптимальность методом потенциалов
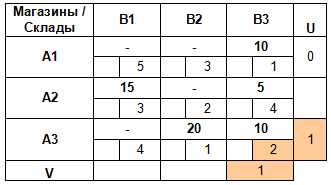
Для каждой свободной клетки плана вычислим разности ΔCij = Cij — (Ui + Vj ), и запишем полученные значения в левых нижних углах соответствующих ячеек.
План является оптимальным, если все разности ΔCij ≥ 0.
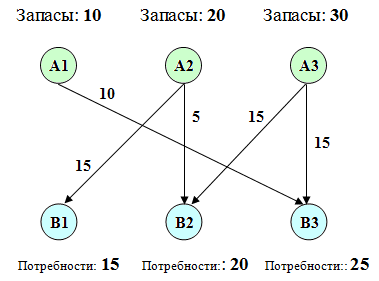
В данном случае план — неоптимальный (ΔC22 граф . Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.
В результате получится граф, аналогичный изображенному ниже:
Все, транспортная задача решена. Поздравляю!
Практическое применение транспортной задачи
Транспортная задача применяется во многих случаях. В частности:
- оптимизация поставок сырья и материалов на производственные предприятия;
- оптимизация доставок товаров со складов в розничные магазины;
- оптимизация пассажирских перевозок.
Это далеко не полный перечень возможностей прикладного использования транспортной задачи.
- Галяутдинов Р. Р. Конспект лекций по логистике
- Решение транспортной задачи в 1С: Предприятие 8.2 // Волшебный форум (@romix). URL: http://kb.mista.ru/article.php?id=859 (дата обращения: 29.10.2013)
- Транспортная задача // Википедия. URL: http://ru.wikipedia.org/wiki/Транспортная_задача (дата обращения: 29.10.2013)
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Метод узловых напряжений
Содержание:
Метод узловых напряжений:
Метод узловых напряжений (узловых потенциалов) является наиболее общим. Он базируется на первом законе Кирхгофа (ЗТК) и законе Ома. В отличие от методов, рассмотренных в лекции 4, метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной количеству рёбер (ветвей) дерева (2.1)
Идея метода состоит в следующем:
- Выбирается базисный узел — один из узлов цепи, относительно которого рассчитываются напряжения во всех узлах; базисный узел помечается цифрой 0.
- Потенциал базисного узла принимается равным нулю.
- Рассчитываются напряжения во всех узлах относительно базисного.
- По закону Ома находятся токи и напряжения в соответствующих ветвях.
Напряжения в узлах цепи, отсчитанные относительно базисного, называют узловыми напряжениями.
Определение:
Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются узловые напряжения, называется методом узловых напряжений.
В дальнейшем будем полагать, что цепь имеет
— задающий ток источника тока, который может быть подключён к
-му узлу; этот ток считается известным и характеризует воздействие на цепь;
— узловое напряжение
-го узла, отсчитанное относительно нулевого (базисного)узла;
— активная проводимость, связывающая £-ый и
-ый узлы;
— ток в ветви между
-ым и
-ым узлами, отсчитываемый от
-го узла в направлении
-го; токи, направления отсчётов которых ориентированы от узла, входят в уравнения со знаком «+ «;
— напряжение в ветви между
-ым и
-ым узлами.
Предварительно покажем, что при известных узловых напряжениях можно найти напряжения на всех элементах цепи, а потому и все токи. Действительно, напряжение на любой ветви определяется по второму закону Кирхгофа (ЗНК) как разность соответствующих узловых напряжений, а токи в элементах найдутся по закону Ома. Для контура, включающего элементы 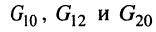
Аналогично можно записать
что и требовалось показать.
Составление узловых уравнений
При составлении уравнений для, схемы рис. 5.1 будем полагать, что задающие токи 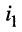
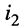
Тогда согласно первому закону Кирхгофа для узлов 1 и 2 в предположении, что в общем случае они связаны со всеми другими узлами, получим:
Выразим токи в уравнениях через узловые напряжения, как показано в разд. 5.1:
Раскрыв скобки и приведя подобные члены, получаем узловые уравнения:
Полученный результат позволяет сделать следующие выводы:
- в левую часть каждого из уравнений входит N слагаемых, пропорциональных искомым узловым напряжениям
- коэффициент при узловом напряжении
-го узла, для которого составляется уравнение, представляет собой сумму проводимостей всех элементов, подключённых одним из своих зажимов к этому узлу; этот коэффициент входит в уравнение с положительным знаком;
- остальные слагаемые представляют собой произведение узлового напряжения на проводимость
элемента, связывающего

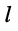
Аналогично записываются узловые уравнения для всех других узлов цепи, в результате чего образуется система узловых уравнений вида:
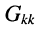


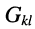

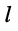

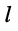
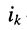



Систему узловых уравнений принято записывать в канонической форме, а именно:
- токи, как свободные члены, записываются в правых частях уравнений;
- неизвестные напряжения записываются в левых частях уравнений с последовательно возрастающими индексами;
- уравнения располагаются в соответствии с порядковыми номерами узлов. Такая запись применена в (5.2).
Система (5.2) является линейной неоднородной 
Метод узловых напряжений даёт существенное сокращение необходимого числа уравнений по сравнению с методом токов элементов. Выигрыш оказывается тем значительнее, чем больше независимых контуров имеет цепь.
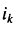
Особенности составления узловых уравнений
Метод узловых напряжений можно применять и в тех случаях, когда в анализируемой цепи имеются источники напряжения. При этом:
- напряжение между любой парой узлов, к которым подключён источник напряжения, известно;
- в качестве базисного желательно выбирать узел, к которому одним из своих зажимов подключён источник напряжения — тогда узловое напряжение, отсчитываемое между базисным узлом и вторым зажимом источника, равно ЭДС источника или отличается от него знаком; кроме того, базисным может быть выбран узел, к которому подключено наибольшее число элементов, если этот выбор не противоречит первой рекомендаций;
- уменьшается число независимых узловых напряжений, а потому понижается и порядок системы, т. е. число входящих в систему независимых уравнений;
- если цепь содержит
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
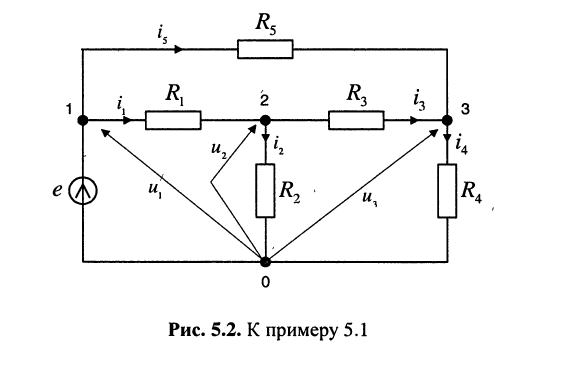
Пример 5.1.
Записать систему узловых уравнений для удлинителя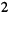
Решение. Удлинитель содержит четыре узла и один источник тока, поэтому согласно (5.3) достаточно составить всего два узловых уравнения
Положим узел 0 базисным, поскольку к нему одним из своих зажимов подключён источник напряжения. Узловое напряжение узла 1 известно и равно. ЭДС источника напряжения 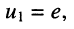
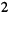
Собственная проводимость второго узла
взаимные проводимости второго узла
собственная проводимость третьего узла
взаимные проводимости третьего узла
Теперь получим систему узловых уравнений, записав узловые уравнения для второго и третьего узлов:
Поскольку 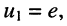
Эта система уравнений и является окончательным результатом решения задачи, поставленной в примере.
Если содержащиеся в цепи источники напряжения не имеют общего зажима, то задачу анализа следует решать или методом узловых напряжений в сочетании с принципом наложения или путём эквивалентных преобразований перейти к другой модели цепи.
При составлении узловых уравнений для цепей, содержащих многополюсники (например, транзисторы, операционные усилители
и т. д), следует прежде всего заменить эти многополюсники их схемами замещения.
Метод узлового напряжения
Расчет сложных разветвленных электрических цепей с несколькими источниками и двумя узлам, можно осуществить методом узлового напряжения. Напряжение межи узлами и называется узловым. UAB R3 узловое напряжение цепи (рис. 4.9) Для различных ветвей (рис. 4.9) узловое напряжение UAB можно опредо лить следующим образом.
1. Поскольку для первой ветви источник работает в режиме генератор:
Величина тока определяется как
где 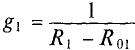
2.Для второй ветви источник работает в режиме потребителя следовательно
3.Для третьей ветви
(Потенциал точки В для третьей ветви больше, чем потенций точки А, так как ток направлен из точки с большим потенциалом в точку с меньшим потенциалом)
Величину тока 
По первому закону Кирхгофа для узловой точки А (или В):
Подставив в уравнение (4.6) значения токов из уравнений (4.3), .4) и (4.5) для рассматриваемой цепи, можно записать
Решив это уравнение относительно узлового напряжения UAB, можно определить его значение
Следовательно, величина узлового напряжения определяется отношением алгебраической суммы произведений ЭДС и проводимости ветвей с источниками к сумме проводимостей всех ветвей:
Для определения знака алгебраической суммы направление токов во всех ветвях выбирают одинаковым, т.е. от одного узла другому (рис. 4.9). Тогда ЭДС источника, работающего в режиме генератора, берется со знаком «плюс», а источника, работающего в режиме потребителя, со знаком «минус». Таким образом, для определения токов в сложной цепи с двумя узлами вычисляется сначала узловое напряжение по выражению 4.9), а затем значения токов по формулам (4.3), (4.4), (4.5). Узловое напряжение UAB может получиться положительным или отрицательным, как и ток в любой ветви.
Знак «минус» в вычисленном значении тока указывает, что реальное направление тока в данной ветви противоположно словно выбранному.
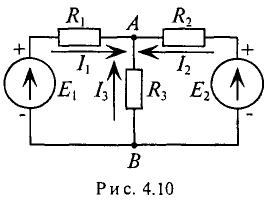
Пример 4.7
В ветвях схемы (рис. 4.10) требуется определить токи, если:
Решение
Узловое напряжение
где
тогда
Токи в ветвях будут соответственно равны
Как видно из полученных результатов, направление токов 
Пример 4.8
Два генератора (рис. 4.11), ЭДС и внутреннее сопротивление которых одинаковы: 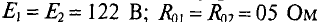
Как изменится ток второго генератора: 1) при увеличении его ЭДС (£2) на 1 %; » 2) при увеличении узлового напряжения (UAB) на 1 %.
Решение
Определяется узловое напряжение UAB цепи (рис. 4.11)
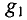
Тогда ток второго генератора
При увеличении Е2 на 1 %, его величина станет равной
При этом
Следовательно, увеличение ЭДС генератора Е2 на 1 % приводит увеличению тока этого генератора на 24 %.
2. При увеличении узлового напряжения на 1% его величины станет равной
При этом 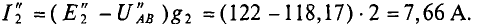
Знак «минус» означает уменьшение, а не увеличение тока 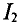
Определение метода узловых напряжений
Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются потенциалы в узлах электрической цепи относительно некоторого базисного узла. Эти разности потенциалов называются узловыми напряжениями, причем положительное направление их указывается стрелкой от рассматриваемого узла к базисному.
Напряжение на какой-либо ветви равно, очевидно, разности узловых напряжений концов данной ветви; произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.
Если принять потенциал базисного узла равным нулю, то напряжения между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.
На рис. 7-7 в виде примера изображена электрическая схема с двумя источниками тока, имеющая три узла: 1, 2 и 3. Выберем в данной схеме в качестве базиса узел 3 и
обозначим узловые напряжения точек 1 и 2 через 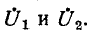
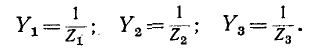
Для заданной электрической цепи с тремя узлами могут быть записаны два уравнения по первому закону Кирхгофа, а именно: для узла 1
Величина 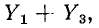
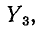
Если заданы токи источников тока и комплексные проводимости ветвей, то узловые напряжения находятся совместным решением уравнений.
В общем случае если электрическая схема содержит q узлов, то на основании первого закона Кирхгофа получается система из q — 1 уравнений (узел q принят за базисный):
Здесь ток источника тока, подходящий к узлу, берется со знаком плюс, а отходящий от узла — со знаком минус; 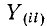
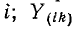
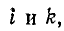
Решив систему уравнений (7-5) при помощи определителей 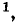
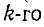
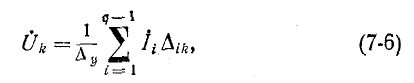
где 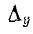
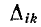
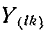
Первый индекс i алгебраического дополнения, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру узла, заданный ток источника тока которого умножается на данное алгебраическое дополнение. Второй индекс 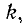
Уравнения (7-5), выражающие первый закон Кирхгофа, записаны в предположении, что в качестве источников электрической энергии служат источники тока. При наличии в электрической схеме источников э. д. с. последние должны быть заменены эквивалентными источниками тока.
Если в схеме имеются ветви, содержащие только э. д, с. (проводимости таких ветвей бесконечно велики), то эти ветви следует рассматривать как источники неизвестных токов, которые затем исключаются при сложении соответствующих уравнений. Дополнительными связями между неизвестными узловыми напряжениями будут являться известные напряжения между узлами, равные заданным э. д. с.
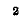
При наличии только одной ветви с э. д. с. и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которому примыкает данная ветвь; тогда напряжение другого узла становится известным и число неизвестных сокращается на одно.
Метод узловых напряжений имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа. Если заданная электрическая схема имеет q узлов и р ветвей, то в соответствии со сказанным выше, метод узловых напряжений представляет преимущество при q — 1
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://galyautdinov.ru/post/transportnaya-zadacha
http://www.evkova.org/metod-uzlovyih-napryazhenij

















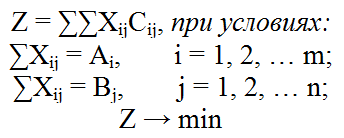
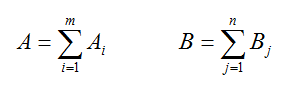
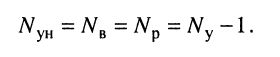
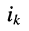 — задающий ток источника тока, который может быть подключён к
— задающий ток источника тока, который может быть подключён к 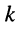 -му узлу; этот ток считается известным и характеризует воздействие на цепь;
-му узлу; этот ток считается известным и характеризует воздействие на цепь;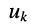 — узловое напряжение
— узловое напряжение 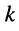 -го узла, отсчитанное относительно нулевого (базисного)узла;
-го узла, отсчитанное относительно нулевого (базисного)узла;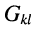 — активная проводимость, связывающая £-ый и
— активная проводимость, связывающая £-ый и 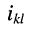 — ток в ветви между
— ток в ветви между 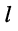 -ым узлами, отсчитываемый от
-ым узлами, отсчитываемый от 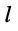 -го; токи, направления отсчётов которых ориентированы от узла, входят в уравнения со знаком «+ «;
-го; токи, направления отсчётов которых ориентированы от узла, входят в уравнения со знаком «+ «;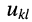 — напряжение в ветви между
— напряжение в ветви между 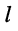 -ым узлами.
-ым узлами.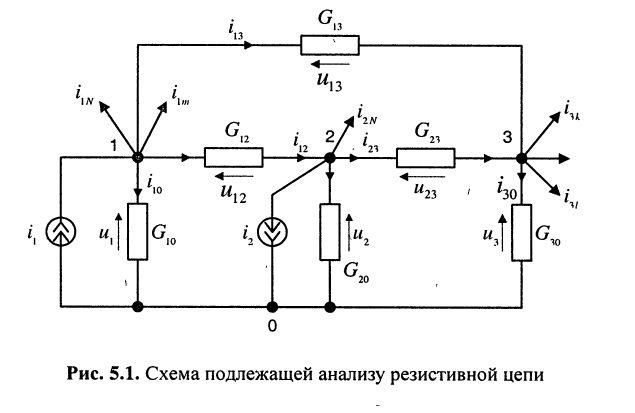
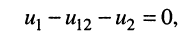
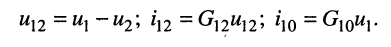
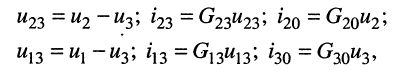
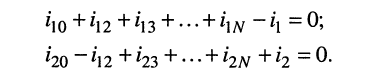
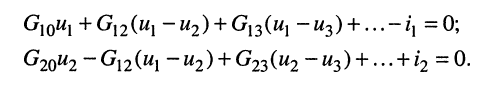
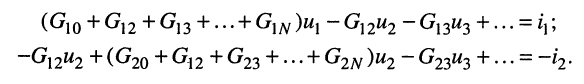
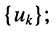
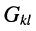 элемента, связывающего
элемента, связывающего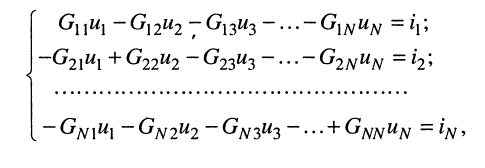
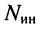 источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно