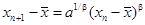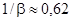Метод приближенного решения уравнений это

Лекция «Приближенные решения алгебраических и трансцендентных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

БИК Курс лекций по дисциплине «Численные методы»

для специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем

Раздел 2. Численные методы

2.1.1. Приближенные решения алгебраических и трансцендентных уравнений

Алгебраические и трансцендентные уравнения

Графический метод решения уравнений

1. Алгебраические и трансцендентные уравнения

При решении практических задач часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде

( x )= g ( x ), (1)

где (х) и g (х) — данные функции, определенные на некотором числовом множестве X , называемом областью допустимых значений уравнения .

В общем случае нелинейное уравнение можно записать в виде:

F ( x ) определена и непрерывна на конечном или бесконечном интервале .

 Совокупность значений переменной х, при которых уравнение (1) превращается в тождество, называется решением этого уравнения, а каждое значение х : из этой совокупности называется корнем уравнения.

 Всякое число , обращающее функцию F ( x ) в нуль, т.е. такое, при котором F ( )=0, называется корнем уравнения (1).

 Число называется корнем k -той кратности, если при x =вместе с функцией F ( x ) равны нулю ее производные до ( k -1) порядка включительно:

F ( ) = F / () = … = F ( k -1) ( ) = 0.

Однократный корень называется простым.

 Решить уравнение – значит найти множество всех корней этого уравнения.

Оно может быть конечным или бесконечным.

 Два уравнения F ( x )=0 и G ( x =0) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, то есть множества решений этих уравнений совпадают.

В зависимости от того, какие функции входят в уравнения (1) или (2), уравнения разделяются на два больших класса: линейные и нелинейные.

Нелинейные уравнения делятся, в свою очередь на: алгебраические и трансцендентные .

Уравнение (2) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:

где a ₀, a ₁, . , a _n — коэффициенты уравнения, а x -неизвестное. Показатель n называется степенью алгебраического уравнения.

Если функция F ( x ) не является алгебраической, то уравнение (1) называется трансцендентным.

В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.

Решение уравнения с одним неизвестным заключается в отыскании корней, т. е. тех значений х, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и невещественными (комплексными).

Найти точные значения корней уравнения можно только в исключительных случаях, обычно, когда есть какая-либо простая формула для вычисления значения корней, выражающая их через известные величины.

Поскольку подавляющее большинство нелинейных уравнений с одной переменой не решаются путем аналитических преобразований (точными методами), на практике их решают только численными методами.

При решении многих практических задач точное решение уравнения не всегда является необходимым. Задача нахождения корней считается решенной, если корни вычислены с заданной степенью точности.

 Решить уравнение – это значит

установить, имеет ли оно корни,

и найти значение корней с заданной точностью.

 Задача численного нахождения действительных и комплексных корней уравнения (2) обычно состоит из двух этапов:

отделение корней, т.е. нахождение достаточно малых окрестностей рассматриваемой области, в которых находится одно значение корня,

и уточнение корней, т.е. вычисление корней с заданной степенью точности в некоторой окрестности.

Наиболее распространенными на практике численными методами решения уравнения (2) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации. Применение того или иного метода для решения уравнения (2) зависит от числа корней, задания исходного приближения и поведения функции F ( x ).

2. Графические методы решения уравнений

Одним из методов решения уравнений является графический. Точность такого решения невелика, однако с помощью графика можно разумно выбрать первое приближение, с которого начнется дальнейшее решение уравнения. Существуют два способа графического решения уравнений.

Первый способ. Все члены уравнения переносят в левую часть, т. е. представляют его в виде f (х) = 0. После этого строят график функции у = f ( x ), где f (х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f (х) с осью Ох и являются корнями уравнения, так как в этих точках у = 0 (рис. 1).

Рисунок 1

Второй способ. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую в правой, т. е. представляют его в виде f (х) = g (х).

После этого строят графики двух функций у = f (х) и у = g (х). Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х₀, ординаты обоих графиков в этой точке равны между собой, т. е. f (х₀) = g (х₀). Из этого равенства следует, что х₀ – корень уравнения (рис. 2).

Рисунок 2

Пример 1. Решить графически уравнение х 3 — 2 x 2 + 2х — 1 = 0.

Первый способ. Построим график функции у = х 3 — 2 x 2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет один корень (рис. 3). (Отметим, что алгебраическое уравнение третьей степени имеет или один действительный корень или три. Так как кривая пересекает ось абсцисс только в одной точке, то данное уравнение имеет только один действительный корень. Остальные два корня – комплексные.)

Рисунок 3 Рисунок 4

Второй способ. Представим данное уравнение в виде х 3 = 2 x 2 + 2х–1 и построим графики функций у = х 3 и у = 2 x 2 + 2х – 1. Найдем абсциссу точки пересечения этих графиков; получим х = 1 (рис. 4).

Пример 2. Найти приближенно графическим способом корни уравнения lg х — Зх + 5 = 0.

Перепишем уравнение следующим образом: lg х = Зх — 5.

Функции в левой и в правой части уравнения имеют общую область определения: интервал 0

Строим графики функций у = lg х и у = Зх — 5 (рис. 5). Прямая у = Зх-5 пересекает логарифмическую кривую в двух точках с абсциссами x ₁ 0,00001 и x ₂ 1,75. На рисунке трудно показать пересечение графиков этих двух функций в первой точке, однако, учитывая, что нижняя ветвь, логарифмической кривой неограниченно приближается к оси Оу, можно предполагать, что пересечение этих двух графиков произойдет вблизи точки пересечения графика функции у = Зх — 5 и оси Оу. Абсцисса точки пересечения приближенно равна 0,00001. Итак, корни уравнения x ₁ 0,00001 и x ₂ 1,75

Рисунок 5 Рисунок 6

Пример 3. Найти графически корни уравнения 2 х = 2х.

Решение. Строим графики функций у = 2 х и у = 2х. Эти графики пересекаются в двух точках, абсциссы которых равны х ₁ = 1 и х ₂ = 2. Данное урав­нение имеет два корня х ₁ = 1 и х ₂ = 2 (рис. 6).

Подводя итог вышеизложенному, можно рекомендовать для графического решения уравнения f (х) = 0, все корни которого лежат в промежутке [а, b ], следующую простую схему.

1. Представить указанное уравнение в виде (х) = g (х) с таким расчетом, чтобы функции у=(х) и у = g (х) были просты и удобны для исследования и построения.

2. На бумаге вычертить графики функций у =(х) и у = g (х) в промежутке [а, b ].

3. Если графики не пересекаются, то корней в данном промежутке нет. Если же графики пересекаются, то нужно определить точки их пересечения, найти абсциссы этих точек, которые и будут приближенными значениями корней рассматриваемого уравнения.

Первый этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении “тесных” промежутков, содержащих только один корень.

 Корень уравнения f (х) = 0 считается отделенным на отрезке [ a , b ] , если на этом отрезке уравнение f (х) = 0 не имеет других корней.

 Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень.

Отделение корней можно произвести двумя способами – графическим и аналитическим.

Графический метод отделения корней. При графическом методе отделения корней поступают так же, как и при графическом методе решения уравнений.

Графический метод отделения корней не обладает большой точностью. Он дает возможность грубо определить интервалы изоляции к орня. Далее корни уточняются одним из способов, указанных ниже.

Аналитический метод отделения корней. Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые свойства функций, изучаемые в курсе математического анализа.

Сформулируем без доказательства теоремы, знание которых необходимо при отделении корней.

1) Если непрерывная на отрезке функция F ( x ) принимает на его концах значения разных знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень

2) Если функция F ( x ) к тому же еще и строго монотонна, то корень на отрезке единственный.

Рассмотрим примеры поведения некоторых функций:

Рисунок 7

Для отделения корней можно эффективно использовать ЭВМ.

Пусть имеется уравнение F ( x )=0, причем можно считать, что все корни находятся на отрезке , в которой функция F ( x ) отделена, непрерывна и F ( A )* F ( B ) F ( x ), начиная с точки X = A , двигаясь вправо с некоторым шагом h .

Как только обнаружится пара соседних значений F ( x ), имеющих разные знаки, и функция F ( x ) монотонна на этом отрезке, так соответствующие значения аргумента X (предыдущее и последующее) можно считать концами отрезка, содержащего корень.

Схема соответствующего алгоритма изображена ниже. Результатом решения поставленной задачи будут выводимые на дисплей в цикле значения параметров X ₁ и X ₂ (Концов выделенных отрезков).

Приближенное вычисление корней в уравнениях

Приближенное вычисление корней в уравнениях

Приближённое решение уравнений :

1.1 Способ хорд (или способ линейной интерполяции).

1. Способ касательных (или способ Ньютона).
2. Комбинированный способ (комбинированное применение способов хорд и касательных).

Приближённое решение уравнений.

Если квадратные уравнения решали уже древние греки, то способы решения алгебраических уравнений третьей и четвёртой степени были открыты лишь в XVI веке. Эти классические способы дают точные значения корней и выражают их через коэффициенты уравнения при помощи радикалов различных степеней. Однако эти способы приводят к громоздким вычислениям и поэтому имеют малую практическую ценность.

В отношении алгебраических уравнений пятой и высших степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как:

Сказанное, однако, не означает отсутствия в науке методов решения уравнения высших степеней. Имеется много способов приближенного решения уравнений — алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих вычислять их корни с любой, заранее заданной степенью точности, что для практических целей вполне достаточно.

На простейших из таких способов мы и остановимся, причём речь будет идти о вычислении действительных корней.

Пусть нужно решить уравнение:

Если обратиться к рисунку, то каждый корень уравнения (1) представляет собой абсциссу точки пересечения графика функции y=f(х)

C осью Ох (рисунок №1)

С помощью графика функции или каким-нибудь иным способом обычно удаётся установить приблизительные значения корней. Это позволяет для каждого корня получить грубые приближения по недостатку и по избытку. Такого рода грубых приближений во многих случаях оказывается достаточно, чтобы, отправляясь от них, получить все значения корня с требуемой точностью. Об этом и пойдёт речь.

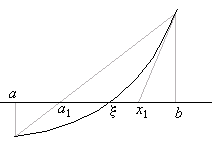
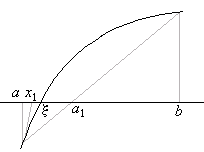
Итак, пусть корень Е уравнения (1) «зажат» между двумя его приближениями а и b по недостатку и по избытку а

Способ хорд (или способ линейной интерполяции).

Проведём хорду АВ (рисунок№3) и за первое приближённое значение корня примем абсциссу x1 точки С пересечения хорды с осью Ох.

Уравнение хорды имеет вид:

Поэтому в точке С:

Рассмотрение всех четырёх случаев, изображённых на рисунке №2, показывает, что точка x1 лежит между a и b с той стороны от Е, где f(х) имеет знак, противоположный знаку f«(х).

Остановим внимание на первом случае: f`(х)>0, f«(х)>0 (рисунок №3), — в остальных случаях рассуждение вполне аналогично. В этом первом случае x1 лежит между a и Е. С отрезком [x1, b] поступаем так же, как мы поступаем с отрезком [a, b] (рисунок №4). При этом для нового приближённого значения корня получаем:

x1 = x2-(b- x1)*f(x1)/f(b)-f(x1)

( в формуле (2) заменяем x1 на x2, а на x1 ); значение x2 оказывается между x1 и Е. Рассматриваем отрезок [x2, b] и находим новое приближённое x3, заключённое между x2 и Е и. т. д. В результате получим последовательность а 0

Найдём первое приближённое значение корня по формуле (2):

так как f(1,588)=-0,817 0

Следовательно, искомый корень с точностью до 0,01 равен 1,64.

1.2 Способ касательных (или способ Ньютона).

В том из концов дуги АВ (рисунок №5), в котором знаки f(х) и f«(х) совпадают, проводим касательную и за первое приближённое значение корня принимаем абсциссу х1` точки Д пересечения этой касательной с осью Ох. Обратимся вновь к первому случаю, соответствующему первому рисунку №2 (f`(x)>0, f«(x)>0), — в остальных случаях рассуждают опять-таки аналогично. Уравнение интересующей нас касательной имеет вид:

и поэтому в точке Д:

Из рисунка видно, что x1` лежит между Е и b. С отрезком [a, x1`] поступаем так же, как с отрезком [a, b] ( рисунок №5), и в результате для нового приближённого значения корня получим:

х2` = x1`- f( x1`)/ f`( x1`).

Значение х2` оказывается между Е и x1`. Рассматриваем отрезок [a, х2`] и находим новое приближение х3` и т. д. В результате получим последовательность:

все более точных приближённых значений корня, причём:

xn+1`= xn`- f(xn`)/ f`( xn`) (8)

Эта формула справедлива для всех четырёх случаев, изображённых на рисунке 32. Для оценки погрешностей полученных приближений можно опять воспользоваться формулой (5), как и в первом случае, легко устанавливается сходимость последовальности x1`, х2`, х3`,…,xn`,… к значению Е

Пример №2. Методом касательных найдём положительный корень уравнения

с точностью до 0,01.

В этом уравнении f(х)=х^4-2x-4, f`(х)=4х^3-2,а f«(х)=12x^2.Так как f(х) и f«(х) при х0 = 1,7 имеют один и тот же знак, а именно:

f(1,7)=0,952>0 и f«(1,7)>0, то применяем формулу:

x1`= х0- f(х0)/ f`( х0), где f`(1,7)=4*1,7^3-2=17,652. Тогда

Применяем второй раз способ касательных:

х2= x1- f(x1)/ f` (x1), где f(x1)= f(1,646)=0,048, f` (1,646) =15,838;

f(1,643)=0,004, f` (1,643)=15,740;

Следовательно, искомый корень с точностью до 0,01 равен 1,64.

1.3 Комбинированный способ

(комбинированное применение способов хорд и касательных).

Этот способ состоит в одновременном использовании способов хорд и касательных. Остановим своё внимание опять на случае, отвечающем первому рисунку №2. Значения x1 и x1`, вычисляем по прежним формулам, т. е. принимаем:

x1`=b-f(b)/f`(b), причём: x1 0 изображён на рисунке №7. Из этого рисунка видно, что уравнение имеет положительный единственный корень, лежащий на отрезке 1 0,f«(x)>0 т. е. знак производных сохраняется. Применяем комбинированный способ:

Формулы (10) дают:

При этом x1`- x1=0,012, т. е. точность недостаточна. Совершаем второй шаг:

При этом х2`- х2=0,00018, т. е. точность достаточна. Таким образом:

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Курсовая работа: Приближённые методы решения алгебраического уравнения

Реферат по курсу численных методов выполнил студент группы РЭ–01-1

Днепропетровский Национальный Университет

Кафедра физики СВЧ

1. Численное решение уравнений с одним неизвестным

В данной работе рассматриваются метода приближённого вычисления действительных корней алгебраического или трансцендентного уравнения

на заданном отрезке [a, b].

Уравнение называется алгебраическим, если заданная функция есть полином n-ой степени:

Требование a₀ ¹ 0 обязательно, так как при невыполнении этого условия данное уравнение будет на порядок ниже.

Всякое уравнение (1.1) называется трансцендентным, если в нём невозможно явным образом найти неизвестное, а можно лишь приближённо.

Однако в число алгебраических уравнений можно также включить те уравнения, которое после некоторых преобразований, можно привести к алгебраическому.

Те методы, которые здесь рассматриваются, применимы, как к алгебраическим уравнениям, так и к трансцендентным.

Корнем уравнения (1.1) называется такое число x, где f(x)=0.

При определении приближённых корней уравнения (1.1) необходимо решить две задачи:

отделение корней, т. е. определение достаточно малых промежутков, в каждом из которых заключён один и только один корень уравнения (простой и кратный);

уточнение корней с заданной точностью (верным числом знаков до или после запятой);

Первую задачу можно решить, разбив данный промежуток на достаточно большое количество промежутков, где бы уравнение имело ровно один корень: на концах промежутков имело значения разных знаков. Там где данное условие не выполняется, те промежутки откинуть.

Вторая задача решается непосредственно в методах рассмотренных ниже.

При графическом отделении корней уравнения (1.1) нужно последнее преобразовать к виду:

Действительно, корнями уравнения (1.1)

являются абсциссы точек пересечения этих графиков (и только они).

Из всех способов, какими можно уравнение (1.1) преобразовать к виду (2.1) выбираем тот, который обеспечивает наиболее простое построение графиков y₁ =j₁ (x) и y₂ =j₂ (x). В частности можно взять j₂ (x) = 0 и тогда придём к построению графика функции (1.1), точки пересечения которого с прямой y₂ =j₂ (x)=0, т. е. с осью абсцисс, и есть искомые корни уравнения (1.0).

Условия, наложенные на функцию f(x) на отрезке [a, b].

Будем предполагать, что функция f(x) непрерывна на отрезке [a, b] (для метода хорд можно потребовать на интервале) и имеет на этом интервале первую и вторую производные, причём обе они знакопостоянны (в частности отличны от нуля). Будем также предполагать, что функция f(x) принимает на концах отрезка значения разного знака. В силу знакопостоянства первой производной функция f(x) строго монотонна, поэтому при сделанных предположениях уравнение (1.1) имеет в точности один корень на интервале (a, b).

2. Метод дихотомии

Этот метод ещё называется методом вилки.

Нам необходимо найти корень уравнения (1.1) на отрезке [a, b]. Рассмотрим отрезок [x₀ , x₁ ]: [x₀ , x₁ ]Ì[a, b]. Пусть мы нашли такие точки х₀ , х₁ , что f (х₀ ) f(х₁ ) £ 0, т. е. на отрезке [х₀ , х₁ ] лежит не менее одного корня уравнения. Найдём середину отрезка х₂ =(х₀ +х₁ )/2 и вычислим f(х₂ ). Из двух половин отрезка выберем ту, для которой выполняется условие

f (х₂ ) f(х_гран .) £ 0, так как один из корней лежит на этой половине. Затем новый отрезок делим пополам и выберем ту половину, на концах которой функция имеет разные знаки, и т. д. (рис 1.2).

Если требуется найти корень с точностью Е, то продолжаем деление пополам до тех пор, пока длина отрезка не станет меньше 2Е. Тогда середина последнего отрезка даст значение корня с требуемой точностью. Дихотомия проста и очень надёжна. К простому корню она сходится для любых непрерывных функций в том числе и не дифференцируемых; при этом она устойчива к ошибкам округления. Скорость сходимости не велика; за одну итерацию точность увеличивается примерно вдвое, т. е. уточнение трёх цифр требует 10 итераций. Зато точность ответа гарантируется.

Приступим к доказательству того, что если непрерывная функция принимает на концах некоторого отрезка [a, b] значения разных знаков, то методом дихотомии однозначно будет найден корень.

Предположим для определённости, что функция f(x) принимает на левом конце отрезка [a, b] отрицательное значение, а на правом – положительное:

Возьмём среднюю точку отрезка [a, b], h=(a+b)/2 и вычислим значение в ней функции f(x). Если f(h)=0, то утверждение теоремы доказано: мы нашли такую точку, где функция обращается в нуль. Если f(h)¹ 0, тогда из отрезков [a, h] и [h, b] выберем один из них тот, где функция на его концах принимает значения разных знаков. Обозначим его [a₁ , b₁ ]. По построению: f(a₁ ) 0. Затем среднюю точку отрезка [a₁ , b₁ ] точку h₁ и проведём тот же алгоритм нахождения другого отрезка [a₂ , b₂ ] где бы по построению f(a₂ ) 0. Будем продолжать этот процесс. В результате он либо оборвётся на некотором шаге n в силу того, что f(h_n )=0, либо будет продолжаться неограниченно. В первом случае вопрос о существовании корня уравнения f(x)=0 решён, поэтому рассмотрим второй случай.

Неограниченное продолжение процесса даёт последовательность отрезков [a, b], [a₁ , b₁ ], [a₂ , b₂ ],… Эти отрезки вложены друг в друга – каждый последующий отрезок принадлежит всем предыдущим:

Длины отрезков с возрастанием номера n стремятся к нулю:

Рассмотрим левые концы отрезков. Согласно (1.2) они образуют монотонно убывающую ограниченную последовательность n >. Такая последовательность имеет предел, который можно обозначить через c₁ :

Согласно (1.1) и теореме о переходе к пределу в неравенствах имеем:

Теперь рассмотрим правые концы отрезков. Они образуют монотонно не возрастающую ограниченную последовательность n >, которая тоже имеет предел. Обозначим его через с₂ : . Согласно неравенству (2.1) пределы с₁ и с₂ удовлетворяют неравенству с₁ £ с₂ . Итак, a_n £ с₁ 0, то чтобы её достигнуть достаточно сделать число шагов N, не превышающее log₂ [(b-a)/e]: N>log₂ [(b-a)/e].

3. Метод итераций

Этот метод называется ещё методом последовательных приближений.

Пусть нам необходимо найти корень уравнения (1.1) на некотором отрезке [a, b].

Предположим, что уравнение (1.0) можно переписать в виде:

Возьмём произвольное значение x₀ из области определения функции j(x) и будет строить последовательность чисел n >, определённых с помощью рекуррентной формулы:

Последовательность n > называется итерационной последовательностью. При её изучении встают два вопроса:

Можно ли процесс вычисления чисел x_n продолжать неограниченно, т. е. будут ли числа x_n принадлежать отрезку [a, b] ?

Если итерационный процесс (2.3) бесконечен, то как ведут себя числа x_n при n®¥

Исследование этих вопросов показывает, что при определённых ограничениях на функцию j(x) итерационная последовательность является бесконечной и сходится к корню уравнения (1.3).

, c=j(c) (3.3)

Однако для того, чтобы провести это исследование нам нужно ввести новое понятие.

Говорят, что функция f(x) удовлетворяет на отрезке [a, b] условию Липшица, если существует такая постоянная a, что для любых x₁ , x₂ , принадлежащих отрезку [a, b] имеет место неравенство:

Величину a в этом случае называют постоянной Липшица.

Если функция f(x), удовлетворяет на отрезке [a, b] условию Липшица, то она непрерывна на нём. Действительно, пусть x₀ – произвольная точка отрезка. Рассмотрим приращение функции f(x) в этой точке:

и оценим его с помощью неравенства (4.3)

Таким образом, , что означает непрерывность функции f(x).

Условие Липшица имеет простой геометрический смысл. Возьмём не графике функции y=f(x) две произвольные точки M₁ и M₂ с координатами (x₁ , f(x₁ )) и (x₂ , f(x₂ )). Напишем уравнение прямой линии, проходящей через эти точки:

где k– тангенс угла наклона прямой у оси Оx и определяется формулой:

Если функция f(x) удовлетворяет на отрезке [a, b] условию Липшица, то при произвольном выборе точек M₁ и M₂ имеем |k|£a. Таким образом, с геометрической точки зрения условие Липшица означает ограниченность тангенса угла наклона секущих, проведённых через всевозможные пары точек графика функции y=f(x).

рис 2.3 геометрическая иллюстрация условия Липшица.

рис 3.3 геометрическая иллюстрация cвязи условия Липшица с предположением о дифференцируемости функции.

Предположим, что функция f(x) имеет на отрезке [a, b] ограниченную производную:

| f ¢(x)| £ m; тогда она удовлетворяет условию Липшица с постоянной a=m. Для доказательс- тва этого утверждения воспользуемся формулой конечных приращений Лагранжа:

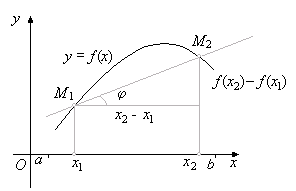
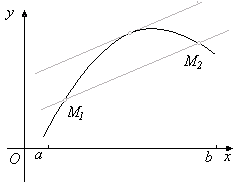
где x₁ , x₂ , — произвольные точки отрезка [a, b] x, — некоторая точка отрезка [x₁ , x₂ ]. Возьмём модуль обеих частей равенства (4.3) и заменим в правой части | f ‘(x)| на m. В результате по- лучим неравенство (4.3) с a=m. Рис.2.3 даёт геометрическую иллюстрацию установленного свойства. Согласно формуле Лагранжа (5.3) каждой секущей графика функции y = f(x) мож- но поставить в соответствие параллельную её касательную. Поэтому наибольший тангенс угла наклона касательных, и его можно оценить той же константой m: |k| £ m.

Познакомившись с условием Липшица, перейдём к изучению итерационной последовательности, предполагая, что уравнение имеет корень x=c. Существование этого корня можно установить с помощью качественного предварительного исследования уравнения с применением теоремы о существовании корня непрерывной функции.

Теорема о существовании корня непрерывной функции

Если функция f(x) непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков, то на этом отрезке существует, по крайней мере, один корень уравнения f(x).

Теорема о сходимости итерационной последовательности

Пусть с – корень уравнения (2.3) и пусть функция j(x) удовлетворяет на некотором отрезке [c-d, c+d] (d>0) условию Липшица с постоянной a 2 |x₀ -c| £ a 2 d

Точка x₂ опять принадлежит отрезку [c-d, c+d] и расположена ближе к точке c, чем точка x₁ , т.е. мы приблизились к c.

По индукции легко доказать, что последующие итерации также существуют и удовлетворяют неравенствам.

Отсюда следует, что:

, т. е.

Остаётся доказать, что корень x=c (1.3) является единственным решением уравнения на отрезке [c-d, c+d]. Действительно, допустим, что существует ещё один корень x=c₁ .

Примем c₁ за нулевое приближение и будем строить итерационную последователь- ность (2.3). Тогда с учётом (7.3) получим x_n =c₁ (n=0, 1, 2, …). С другой стороны, по доказанному , т. е. c₁ =c. Никаких других решений уравнение на отрезке иметь не может.

Сходимость итерационной последовательности к корню уравнения (1.3) может быть использована для приближённого определения корня с любой степенью точности. Для этого нужно только провести достаточное количество итераций.

4. Быстрота сходимости процесса итераций

Используем теперь производную функции j(x) для оценки скорости сходимости итераций при решении уравнения х=j(x). Нужно оценить скорость, с которой убывают погрешности a_n =x-x_n приближённых значений х₁ , … , х_n , … корня x.

Можно заметить, что справедливы равенства x=j(x) и х_{n+ 1} =j(х_n ). Из них вытекает, что:

Но по формуле Лагранжа имеем:

где c_n — точка лежащая между точками x и х_n . Поэтому:

Из равенства (1.4) вытекает следующий вывод:

Пусть x – корень уравнения x=j (x) — лежит на отрезке [a, b]. Если на этом отрезке выполняется неравенство |j ¢(x)| n ·|a₁ | (2.4)

В самом деле, из равенства (1.4) имеем:

Но точка c₁ лежит на отрезке [a, b] (рис.1.4), и потому:

Тем самым наше утверждение доказано.

Так само при 0 n ·|a₁ |.

Точно так же можно доказать, что если на отрезке [a, b] выполнено неравенство:

то процесс итераций расходится.

Особенно быстро сходится процесс последовательных приближений, если в точке x производная функции j(x) обращается в нуль. В этом случае по мере приближения к x, значение j ¢(x) стремится к нулю. Так как:

то сходимость процесса ускоряется по мере приближения к точке x.

Однако то же самое можно наблюдать в методе Ньютона, при замене f(x)=0 на имеем: и её производная: в точке x: f(x)=0 — в методе Ньютона наблюдается ускорение сходимости процесса приближений.

5. Метод касательных (метод Ньютона)

Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x₀ и запишем в ней уравнение касательной к графику функции f(x):

Графики функции f(x) и её касательной близки около точки касания, поэтому естественно ожидать, что точка x₁ пересечения касательной с осью Ox будет расположена недалеко от корня c (рис. 1.5)

Для определения точки имеем уравнение:

Повторим проделанную процедуру: напишем уравнение касательной к графику функции f(x) при x=x₁ и найдём для неё точку пересечения x₂ с осью Ox (см. рис.1.5) x₂ =x₁ – f (x₁ )/ f ¢(x₁ ). Продолжая этот процесс, получим последовательность n >, определён- ную с помощью рекуррентной формулы:

Построение последовательности n >по методу касательных

При исследовании этой последовательности, как и последовательности метода итераций, встают два вопроса:

Можно ли процесс вычисления чисел x_n продолжать неограниченно, т. е. будут ли числа x_n принадлежать отрезку [a, b] ?

Если процесс (3.5) бесконечен, то как ведёт себя последовательность n > при n®¥ ?

При анализе этих вопросов предположим, что корень x=c является внутренней точкой отрезка [a, b] (a 0, | f ¢¢(x)|£M, xÎ[a, b], (4.5)

и докажем следующую теорему.

Теорема о сходимости метода касательных.

Если функция f(x) удовлетворяет условиям, сформулированным п.1., то найдётся такое d: 0 2 /(2M)

Тогда в силу (8.5) для данного e можно указать такое d: 0 ас, так как ас 2 — b — 1 = 0 (3.7)

Только положительный корень b квадратного уравнения (3.6) соответствует убыванию ошибки, т. е. сходящемуся процессу. Следовательно, в методе секущих

,

в то время как в методе Ньютона ошибка убывает быстрей (соответствуя b=2). Но в методе на каждой итерации надо вычислять и функцию, и производную, а в методе секущих – только функцию. Поэтому при одинаковом объёме вычисления в методе секущих можно сделать вдвое больше итераций и получить более высокую точность. Что является более приемлемым при численных расчётах на ЭВМ, чем метод касательных.

В знаменателе формулы (1.7) стоит разность значений функции. Вдали от корня это несущественно; но вблизи корня, особенно корня высокой кратности, значения функции малы и очень близки. Возникает потеря значащих цифр, приводящая к «разболтке» счёта. Это ограничивает точность, с которой можно найти корень; для простых корней это ограничение невелико. Приводить к общему знаменателю уравнение (1.7) не следует: может увеличится потеря точности в расчётах.

От «разболтки» страхуются так называемым приёмом Гарвика. Выбирают не очень малое e, ведут итерации до выполнения |x_{n + 1} -x_n | 0, a f(x), a > x > b

В частности, если х₀ корень уравнения (1.1): f(x₀ ) = 0, отсюда следует, что

C (3.8) и (4.8) получаем:

поэтому из (5.8) следует x₁ 0, a 0,

, f(a₁ ) 0

Если случайно окажется, что точка а₃ , вычисленная по формуле (1.9), лежит за пределами отрезка [a, b], то на следующем шаге надо вместо этой точки взять ближайший к ней конец этого отрезка (рис. 1.9, б). Оказывается, что сходимость усовершенствованного метода хорд гораздо быстрее, чем у обычного. Именно, если x — корень уравнения f(x)=0, то:

|a_{n + 1} | S , где

10. Комбинированный метод решения уравнений

При решении уравнений часто комбинируют методы хорд и Ньютона. Если график функции y=f(x) обращён вогнутостью вверх, то находят точки а₁ и х₁ по формулам:

(1.10)

(2.10)

Если же график функции y=f(x) обращён вогнутостью вниз, то точку а₁ находят по формуле (1.10), а точку х₁ – по формуле:

(3.10)

Как видно из рис.1.10 а) и б), корень x уравнения f(x)=0 лежит обычно между полученными точками а₁ и х₁ . Применяя снова к этим точкам формулы метода хорд и метода Ньютона, получают новую пару точек а₂ и х₂ и т. д.

Таким путём получают две последовательности точек а₁ , а₂ , а₃ , …, a_n , … и x₁ , x₂ , x₃ , … , x_n , …, приближаются с разных сторон к искомому корню x. Преимущество описанного метода состоит в том, что при нём получаются приближённые значения как с избытком так и с достатком.

11. Заключительные замечания

Ситуация, когда одну и ту же задачу можно решить многими способами, является довольно типичной. В таких случаях естественно возникает необходимость сравнения их между собой.

При оценке эффективности численных методов существенное значение имеют различные свойства:

простота организации вычислительного процесса и контроля над точностью;

Наиболее универсальным является метод деления пополам (дихотомии): он только требует непрерывности функции. Остальные методы накладывают более сильные ограничения. Во многих случаях это преимущество метода вилки может оказаться существенным.

С точки зрения организации вычислительного процесса все виды численного нахождения корней уравнения очень просты. Однако и здесь метод деления пополам обладает некоторым преимуществом. Вычисления можно начинать с любого отрезка [a, b], на концах которого непрерывная функция f(x) принимает значения разных знаков. Процесс будет сходится к корню уравнения f(x)=0, причём на каждом шаге он даёт для корня двустороннюю оценку, по которой легко определить достигнутую точность. Сходимость же метода итераций или касательных зависит от того, насколько удачно выбрано нулевое приближение.