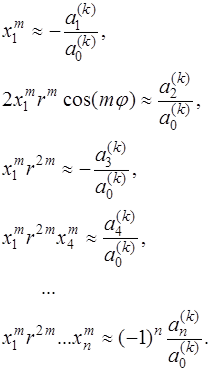Метод приближенного решения уравнений лобачевского

» Метод Лобачевского для приближённого решения уравнений». ( Исследовательская работа. Областная научно-практическая конференция учащихся, посвящённая 220-летию со дня рождения Н.И.Лобачевского. Диплом 3 степени.)

Актуальность исследования заключается в том, что решения уравнений представляет собой одну из существенных задач прикладного анализа, потребность в которой возникает в многочисленных и самых разнообразных разделах физики, механики, техники. Но многие уравнения настолько сложны, что возрастает значение методов приближённого решения уравнений.

Объект исследования: уравнение , методы Ньютона,Мюллера и Лобачевского для его приближенного решения.

Предмет исследования: понять, насколько велика значимость метода Лобачевского .

Гипотеза исследования : метод Лобачевского превосходит другие методы по многим параметрам.

Цель работы: сравнить различные методы приближённого решения уравнений; выяснить их « плюсы» и « минусы», определить место метода Лобачевского среди других методов.

Скачать:

Вложение	Размер
метод Лобачевского	352.5 КБ

Предварительный просмотр:

Муниципальное бюджетное общеобразовательное учреждение Ставровская средняя общеобразовательная школа

Секция « Математический анализ»

Тема: «Метод Лобачевского для приближенного решения уравнений»

Выполнил: Процун Григорий Валерьевич, 11 класс

Руководитель: Мартынова Светлана Вячеславовна

Основная ( содержательная часть)______________________________________6-10

Разумное использование современной вычислительной техники не мыслимо без умелого применения методов приближенного и численного анализа.

Численные методы направлены на решение задач, которые возникают на практике. Решение задачи численными методами сводятся к арифметическим и логическим действиям над числами, что требует применение вычислительной техники. Условия и решения задач чаще всего являются приблизительными, т.е. имеют погрешности, причиной которых являются несоответствие построенной математической модели реальному объекту, погрешность исходных данных, погрешность метода решения, погрешность округления и т.д.

Решение уравнений – алгебраических или трансцендентных – представляет собой одну из существенных задач прикладного анализа, потребность в которой возникает в многочисленных и самых разнообразных разделах физики, механики, техники и естествознания в широком смысле этого слова.

Объект исследования: уравнение , методы Ньютона,Мюллера и Лобачевского для его приближенного решения.

Предмет исследования : понять, насколько велика значимость метода Лобачевского .

Гипотеза исследования : метод Лобачевского превосходит другие методы по многим параметрам.

Цель работы : сравнить различные методы приближённого решения уравнений; выяснить их « плюсы» и « минусы», определить место метода Лобачевского среди других методов.

1.Изучить теоретический материал по теме.

2.Обосновать выбор уравнения .

3. Решить данное уравнение методами Ньютона, Мюллера и Лобачевского.

4. Сравнить данные методы.

5. Сделать выводы.

Информационной базой для написания исследовательской работы послужили труды различных учёных.

Методы исследования : изучение и использование научных и учебных изданий, метод сравнения, сопоставления полученных фактов; аналитический метод.

Теоретическая и практическая ценность полученных результатов, возможность их использования : данная работа предназначена для ознакомления заинтересованным учащимся; материалы можно использовать на уроках и занятиях математического кружка, где математикой занимаются на достаточно высоком уровне.

При выполнении данной исследовательской работы мной были предприняты следующие действия :

— изучены информационные источники;

— изучены и использованы различные методы для решения уравнения;

— сравнил данные методы;

Основная ( содержательная часть).

Настоящая исследовательская работа посвящена нескольким методам решения алгебраических уравнений: методу Лобачевского, Ньютона и Мюллера.

Целью данной работы является: сравнить различные методы приближенного решения уравнений, выявить их плюсы и минусы, определить место метода Лобачевского среди других методов.

Для исследования я решил использовать уравнение

При выборе уравнения я руководствовался следующими соображениями:

1) степень многочлена не должна быть очень высокой

2) уравнение должно иметь иррациональные корни

3) уравнение должно иметь комплексные корни

4) коэффициенты должны быть достаточно большими

Исходное уравнение я получил, перемножая многочлены

и . Соответственно исходное уравнение имеет четыре корня:

Далее я буду действовать так, будто ничего не знаю об этом уравнении.

Следует вычислить производную функции:

Также понадобится схема Штурма:

сначала нужно взять исходный многочлен, затем его производную; поделить многочлен на производную и записать остаток; поделить производную на остаток и записать следующий остаток; поделить первый остаток на второй и так далее, пока не получим число. Большой точности не требуется, коэффициенты можно округлить до десятых. Для данного многочлена схема Штурма выглядит следующим образом:

Далее нужно определить знаки данных многочленов при стремлении х к и (табл.1) . Разность между количеством перемен знаков показывает количество действительных корней, в данном случае их два.

Для методов Ньютона и Мюллера необходимо знать промежутки, на которых находятся корни. Для этого нужно производную приравнять к нулю и решить получившееся уравнение:

Так как мы знаем, что исходное уравнение имеет два корня, то можно сказать, что корни лежат на промежутках от минус бесконечности до -9 и от нуля до плюс бесконечности. Следует заметить, что данные действия можно проделать не всегда.

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции . Метод был впервые предложен английским физиком , математиком и астрономом Исааком Ньютоном ( 1643 — 1727 ). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации . Метод обладает квадратичной сходимостью . Улучшением метода является метод хорд и касательных . Также метод Ньютона может быть использован для решения задач оптимизации , в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.

Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» ( лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу , и в работе «Метод флюксий и бесконечные ряды» ( лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» ( лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году . В своих работах Ньютон вводит такие понятия, как разложение функции в ряд , бесконечно малые и флюксии ( производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону , вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам . Он вычислял не последовательные приближения x n , а последовательность полиномов и в результате получал приближённое решение.

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году , по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» ( лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений x n вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента .

В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» ( англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов .

Чтобы численно решить уравнение методом простой итерации , его необходимо привести к следующей форме: , где — сжимающее отображение .

Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде

В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:

С учётом этого функция определяется выражением:

Эта функция в окрестности корня осуществляет сжимающее отображение, и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:

По теореме Банаха последовательность приближений стремится к

При применении метода Ньютона для решения исходного уравнения я сразу же столкнулся с проблемой выбора исходного приближения, но решил эту проблему, вычислив промежутки, на которых находятся корни. Это я сделал в введении . И в качестве начальных приближений я взял крайние точки данных промежутков, то есть -9 и 1 (0 не подходит, так как производная равна нулю, и выражение, используемое при решении не имеет смысла).

Итак, вычисления производятся по формуле

с помощью калькулятора (как и все остальные вычисления).

Все результаты я поместил в таблицы (табл. 2 и табл. 3). Как видно для вычисления первого корня с точностью до семи знаков после запятой (все вычисления будут проводиться с точностью до семи знаков после запятой) понадобилось четыре приближения, что не очень много, однако для вычисления второго корня понадобилось уже четырнадцать приближений, что достаточно много. Также стоит заметить, что вычисления корней проводятся отдельно друг от друга.

Метод Мюллера — итерационный численный метод для вычисления корня заданной функции f(x) = 0. Был представлен Давидом Мюллером в 1956 году.

Метод Мюллера основан на методе секущих , который строит на каждом шаге итерации прямые , проходящие через две точки на графике f. Вместо этого, метод Мюллера использует три точки, строит параболу , проходящую через эти три точки, и в качестве следующего приближения берёт точку пересечения параболы и оси x .

Этот метод более сложен, чем метод Ньютона, так как здесь необходимо вычисление четырех дополнительных переменных и использование трех начальных приближений, а не одного.

При использовании этого метода так же, как и в методе Ньютона, возникает проблема выбора начальных приближений, но и решается она аналогично. В качестве начальных приближений я выбрал 1; 2; 3 и -9; -10; -11.

Вычисления производятся по формулам:

Результаты я оформил в виде таблиц (табл. 4 и табл. 5). Как видно для вычисления первого корня необходимо десять приближений, а для второго – шесть. Это достаточно много, учитывая сложность вычисления. Корни здесь также вычисляются отдельно.

Метод Лобачевского (Лобачевского-Греффе) – результат труда одного из величайших математиков.

При вычислении этим методом используются следующие формулы:

где a i коэффициент многочлена , k – это не степень, а номер шага

На первый взгляд формулы сложны. Но при упрощении получаем:

Вычисления я поместил в таблицы (табл. 6 и табл. 7). Как видно приближений всего лишь пять, и корни вычисляются вместе.

Также возможно вычисление комплексных корней. Для этого нужно вычислить коэффициенты p и q, а затем решить уравнение :

Результаты в таблицах (табл.8 и табл.9).

Таким образом плюсы и минусы рассмотренных методов в следующем:

Сложность подбора начальных приближений для методов Ньютона и Мюллера.
Для методов Ньютона и Мюллера не всегда удается найти промежутки монотонности функции
В методе Мюллера схема вычисления достаточно сложна
В методах Ньютона и Мюллера требуется больше интераций, чем в методе Лобачевского
В методах Ньютона и Мюллера построение последовательности приближений может зациклиться или быть очень запутанным
Метод Лобачевского не подходит для поиска кратных корней и корней близких по модулю
В методе Лобачевского приходится находить корни высоких степеней
Метод Ньютона достаточно прост
Логический аппарат метода Лобачевского весьма мал

Поэтому можно сказать, что метод Лобачевского один из самых эффективных методов вычислений, который при небольшом количестве итераций дает результат с довольно хорошей точностью, поэтому сфера использования этого метода на практике может быть очень широкой . Метод особенно подходит для использования в компьютерных программах. И мне это может понадобиться для моей будущей профессии (я хочу стать фармацевтом), так как метод Лобачевского применяется в задачах по оптимизации в различных физических и химических моделях. Поэтому эта тема очень перспективна. Одна из перспектив – улучшение данного метода, уже есть несколько удачных попыток.

Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. Вузов. —М.: Высш. шк., 1986.
Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы — 8-е изд.. — М.: Лаборатория Базовых Знаний, 2000.
Вавилов С. И. Исаак Ньютон . — М.: Изд. АН СССР, 1945.
Волков Е. А. Численные методы. — М.: Физматлит, 2003.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ — М.: Мир, 1985.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.

Биография Н.И. Лобачевского.

Лобачевский, Николай Иванович (рис.1) — великий математик, один из творцов неевклидовой геометрии. Родился 22 октября 1793 г. в Нижегородской губернии. Учился в Казанском университете; рано обратил на себя внимание успехами в математике, но аттестован инспекцией как «юноша упрямый, нераскаянный, весьма много о себе мечтательный», проявляющий даже «признаки безбожия». Только заступничество профессоров предотвратило исключение Лобачевского из университета и доставило ему в 1811 г.; после данного им обещания исправиться, степень магистра. К тому же году относятся первые (ненапечатанные) работы Лобачевского: комментарий на один из вопросов «Небесной механики» Лапласа и мемуар, написанный под влиянием изучения «Disquisitiones Arithmeticae» Гаусса и его наблюдения над большой кометой.

В 1814 г. Лобачевский получил звание адъюнкта и приступил к чтению лекций по теории чисел. В последующие годы Лобачевский читал лекции по самым разнообразным отделам математики, а также по физике и астрономии; вместе с тем, он привел в порядок библиотеку университета, упорядочил издательскую его деятельность, позаботился о возведении ряда построек для университета. После ухода Магницкого Лобачевский, тому времени ординарный профессор, был избран в ректоры (1827) и занимал эту должность в течение 19 лет.

В 1828 г. он произнес замечательную речь «О важнейших предметах воспитания», в которой отразилось его увлечение просветительными идеями XVIII столетия. В 1846 — 1855 годах Лобачевский занимал должность помощника попечителя казанского учебного округа.

Скончался 12 февраля 1856 г. Громкая слава Лобачевского основана на его геометрических изысканиях, начатых в 1814 — 1817 годах. Сохранившаяся запись лекций Лобачевского, читанных в эти годы, показывает, что первоначально Лобачевский стоял на традиционной точке зрения, предлагая разные доказательства аксиомы параллельных линий; но уже в 1823 г., в составленном им учебнике геометрии (издан в 1910 г. казанским физико-математическим обществом), он высказался в том смысле, что «строгого доказательства сей истины до сих пор не могли сыскать; какие были даны. не заслуживают быть почтены в полном смысле математическими доказательствами».

К 1826 г. он пришел к определенной формулировке своей новой геометрической системы, которую назвал «воображаемой геометрией» в отличие от «употребительной», евклидовой. О сущности геометрии Лобачевского см. Геометрия (Брокгауз-Ефрон, XIII, 97 и сл.). Гениальное открытие Лобачевского, сделанное им независимо от одновременных работ других геометров, было им впервые сжато изложено в феврале 1826 г. в заседании отделения физико-математических наук (см. «О началах геометрии», «Казанский Вестник», 1829 — 1830) и затем наиболее полно развито в «Новых началах геометрии с полной теорией параллельных» («Ученые Записки Казанского университета», 1835 — 1838). Совершенно не понятый соотечественниками, Лобачевский постарался ознакомить со своей системой западноевропейских ученых и напечатал в 1837 г. «Geometrie imaginaire» («Journal Crelle»), в 1840 г. — «Geometrische Untersuchungen zur Theorie der Parallellinien» (Берн) и в 1855 г., с напряжением последних сил, почти уже ослепший — «Pangeometrie ou precis de geometrie, fondee sur une theorie generale et rigoureuse des paralleles» (в юбилейном сборнике Казанского университета, Казань, 1856). Однако, и за границей идеи Лобачевского остались непонятыми: единственный человек, по достоинству их оценивший, Гаусс, при жизни воздерживался от открытого признания неевклидовой геометрии.

В 1860-х годах была опубликована переписка Гаусса, где он свидетельствует, что развитие неевклидовой геометрии сделано у Лобачевского «мастерски в истинно геометрическом духе». С тех пор заслуги Лобачевского постепенно приобретают общее признание. Сочинения Лобачевского переводятся на иностранные языки; Казанский университет, по почину француза Гуэля, предпринимает издание «Полного собрания сочинений по геометрии Лобачевского» (Казань, 1883 — 1886); в 1893 г., к столетию со дня рождения Лобачевского, ему воздвигается на собранные международной подпиской средства памятник в Казани, и учреждается премия его имени за сочинения по неевклидовой геометрии. При жизни Лобачевского известность доставили ему труды по другим вопросам математики и здесь в некоторых отношениях он предвосхитил позднейшее развитие науки (различение непрерывности и дифференцируемости, слитное изложение планиметрии и стереометрии).

Реферат

РЕФЕРАТ

Записка с., 4 табл., 2 приложения, 5 источников.

АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ, КОРНИ УРАВНЕНИЯ, ЧИСЛО ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ УРАВНЕНИЯ, ТЕОРЕМА ШТУРМА, МЕТОД ЛОБАЧЕВСКОГО–ГРЕФФЕ, МЕТОД ЛИНА, МЕТОД БЕРНУЛЛИ, МЕТОД БРОДЕТСКОГО–СМИЛА.

В курсовом проекте рассмотрен способ приближенного нахождения корней алгебраического уравнения – метод Лобачевского–Греффе. В работе определена идея метода, его вычислительная схема, найдены условия применимости метода, условия сходимости к точному решению, дана характеристика метода с точки зрения его точности. Приведена программная реализация метода Лобачевского–Греффе для случая пары комплексно–сопряженных корней на ЭВМ.

СОДЕРЖАНИЕ

1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 8

1.1 Постановка задачи 8

1.2 Алгебраических уравнений 9

1.2.1 Основные понятия об алгебраическом уравнении 9

1.2.2 Оценка границ модулей корней уравнения 10

1.2.3 Корни алгебраического уравнения 11

1.2.4 Число корней полинома в некоторой области 12

1.2.5 Число действительных корней полинома 13

1.2.6 Теорема Бюдана–Фурье 16

1.3 Метод Лобачевского–Греффе для приближенного решения алгебраических уравнений 19

1.3.1 Идея метода 19

1.3.2 Квадрирование корней 21

1.3.3 Метод Лобачевского-Греффе для случая комплексных корней 24

1.3.4 Модификация метода Лобачевского–Греффе. Метод Бродетского–Смила 25

1.3.5 Потеря точности в методе Лобачевского–Греффе 28

1.4 Другие методы решения алгебраических уравнений с комплексными корнями 28

1.4.1 Метод Бернулли 29

1.4.2 Метод Лина 30

2.1 Задание 1 32

2.2 Задание 2 35

2.3 Описание программного продукта 38

2.3.1 Программа Strum 38

2.3.2 Программа MLG 38

2.4 Анализ полученных результатов 39

ПЕРЕЧЕНЬ ССЫЛОК 41

ПРИЛОЖЕНИЕ А 42

ПРИЛОЖЕНИЕ В 45

ВСТУПЛЕНИЕ

Вычислительная техника наших дней представляет собой мощные средства для фактического выполнения счетной работы. Благодаря этому во многих случаях стало возможным отказаться от приближенной трактовки прикладных вопросов и перейти к решению задач в точной постановке. Разумное использование современной вычислительной техники не мыслимо без умелого применения методов приближенного и численного анализа.

Курс “Численные методы” занимает одно из ведущих мест среди дисциплин, которые изучают студенты специальностей ПМ, САУ, ИНФ.

Численные методы направлены на решение задач, которые возникают на практике. Решение задачи численными методами сводятся к арифметическим и логическим действиям над числами, что требует применение вычислительной техники. Условия и решения задач чаще всего являются приблизительными, т. е. имеют погрешности, причиной которых являются несоответствие построенной математической модели реальному объекту, погрешность исходных данных, погрешность метода решения, погрешность округления и т. д. Целью дисциплины “Численные методы” является поиск наиболее эффективных методом решения конкретной задачи.

Настоящий курсовой проект посвящен одному из методов решения алгебраических уравнений – методу Лобачевского–Греффе.

Цель работы данной рассмотреть идею метода Лобачевского–Греффе для решения алгебраических, привести вычислительную схему нахождения действительных и комплексных корней, определить условия применимости метода, условия сходимости метода к точному решению, привести условную погрешность вычислений.

В курсовом проекте рассмотрены основные теоретические вопросы, связанные нахождением корней алгебраических уравнений. Помимо метода Лобачевского–Греффе рассмотрены методы Лина, метод Бернулли, метод Бродетского–Смила, приведены основные принципы этих методов, указаны условия применимости.

В практической части данной работы приведен комплекс программ, реализующий решение алгебраических уравнений методом Лобачевского–Греффе. Рассмотрены примеры нахождения приближенного решения уравнений данным методом.

1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1 Постановка задачи

Пусть даны множество X элементов x и множество Y с элементами y. Допустим, кроме того, что на множестве X определен оператор , который ставит в соответствие каждому элементу x из Х некоторый элемент y из Y. Возьмем какой-нибудь элемент и поставим себе целью найти такие элементы , для которых является изображением.

Такая задача равносильна решению уравнения

(1.1)

Для него могут быть поставлены следующие проблемы.

1. Условия существования решения уравнения.

2. Условие единственности решения уравнения.

3. Алгоритм решения, следуя которому, можно было бы найти, в зависимости от поставленной цели и условий, точно или приближенно все решения уравнения (1.1), или какое-либо одно решение, заранее указанное, или любое из числа существующих.

Далее будем рассматривать уравнения, в которых x и y будут численными величинами, X, Y – множествами их значений, а оператором будет некоторая функция. В этом случае уравнение (1.1) можно будет записать в виде

(1.2)

В теории численных методов стремятся построить вычислительный процесс, при помощи которого можно найти решение уравнения (1.2) с наперед заданной точностью. Особенно большое значение имеют сходящиеся процессы, позволяющие решить уравнение с любой, сколь угодно малой погрешностью.

Наша задача – нахождение, вообще говоря, приближенное, элемента . Для этой цели разрабатывается алгоритм, который выдает последовательность приближенных решений , причем так, что имеет место соотношение

Такое описание действий, конечно, является несколько идеализированным. Обычно получают какой-либо алгоритм построения последовательности , но фактически реализуется лишь несколько его шагов, т. е. получают только несколько первых членов этой последовательности.

1.2 Алгебраических уравнений

1.2.1 Основные понятия об алгебраическом уравнении

Рассмотрим алгебраическое уравнение n-й степени

, (1.3)

где коэффициенты – действительные числа, причем .

В общем случае будем считать, что – комплексная переменная.

Теорема 1.1 (основная теорема алгебры). Алгебраическое уравнение n-й степени (1.3) имеет ровно n корней, действительных и комплексных, при условии, что каждый корень считается столько раз, какова его кратность.

При этом говорят, что корень уравнения (1.3) имеет кратность s, если

, .

Комплексные корни уравнения (1.3) обладают свойством парной сопряженности.

Теорема 1.2. Если коэффициенты алгебраического уравнения (1.3) – действительные, то комплексные корни этого уравнения попарно комплексно-сопряженные, т. е. если (– действительные числа) есть корень уравнения (1.3), кратности s, то число также является корнем этого уравнения и имеет ту же кратность s.

Следствие. Алгебраическое уравнение нечетной степени с действительными коэффициентами имеет по меньшей мере один действительный корень.

1.2.2 Оценка границ модулей корней уравнения

Можно дать грубую оценку модулей корней уравнения (1.3)

Теорема 1.3. Пусть

где – коэффициенты уравнения (1.3).

Тогда модули всех корней (k=1,…,n) уравнения удовлетворяют неравенству

, (1.4)

т. е. корни этого уравнения на комплексной плоскости расположены внутри круга .

Следствие. Пусть и . Тогда все корни уравнения (1.3) удовлетворяют неравенству

, (1.5)

т. е. корни уравнения (1.3) расположены в круговом кольце .

1.2.3 Корни алгебраического уравнения

Если – корни уравнения (1.3), то для левой части справедливо разложение

. (1.6)

Произведя перемножение биномов в формуле (1.6) и приравнивая коэффициенты при одинаковых степенях x в левой и правой частях равенства (1.6), получим соотношения между корнями и коэффициентами алгебраического уравнения (1.3):

(1.7)

Если учитывать кратности корней, то разложение (1.6) принимает вид

где –различные корни уравнения (1) и – их кратности, причем .

Производная выражается следующим образом:

где Q(x) – полином такой, что

при k=1,2,…,m

является наибольшим общим делителем полинома и его производной , и может быть найден с помощью алгоритма Евклида [4]. Составим частное

и получим полином

с действительными коэффициентами , А1, A2,…, Am, корни которого различны.

Таким образом, решение алгебраического уравнения с кратными корнями сводится к решению алгебраического уравнения более низкого порядка с различными корнями.

1.2.4 Число корней полинома в некоторой области

Полное число корней уравнения , расположенных на комплексной плоскости внутри простого замкнутого контура Г, можно определить на основании следующей теоремы

Теорема 1.4. Если полином P(x) не имеет корней на замкнутом контуре Г, то число корней N этого полинома внутри контура Г в точности равно изменению Arg P(x) при положительном обходе контура Г, деленному на , т. е.

Arg P(x),

причем каждый корень считается столько раз, какова его кратность.

Если уравнение контура Г есть

, ,

где t – параметр, то для определения числа N на плоскости XOY строят кривую

, , (1.8)

(X(t), Y(t) – действительные функции), и подсчитывают, сколько оборотов N делает кривая (1.9) делает вокруг начала координат.

1.2.5 Число действительных корней полинома

Общее представление о числе действительных корней уравнения (1.3) на интервале (a, b) дает график функции , где корнями являются абсциссы точек пересечения графика с осью Ox.

Отметим некоторые свойства полинома P(x):

1. Если P(a)P(b) 0, то на интервале (a, b) существует четное число или не существует вообще корней полинома P(x).

Вопрос о числе действительных корней алгебраического уравнения на данном промежутке решается методом Штурма.

Определение. Пусть дана упорядоченная конечная система действительных чисел, отличных от нуля:

,,…, (1.9)

Говорят, что для пары рядом стоящих элементов , системы (1.9) имеется изменение знака, если эти элементы обладают противоположными знаками, т. е.

и нет изменения знака, если знаки их одинаковы, т. е.

Определение. Общее число изменений знаков всех пар соседних элементов , системы (1.9) называется числом перемен знаков в системе (1.9).

Определение. Для данного полинома P(x) системой Штурма называется система полиномов [1]

, , , ,…, ,

где , – взятый с обратным знаком остаток при делении полинома на , – взятый с обратным знаком остаток при делении полинома на и т. д.

Замечание 1. Если полином не имеет кратных корней, то последний элемент системы Штурма есть отличное от нуля действительное число.

Замечание 2. Элементы системы Штурма можно вычислять с точностью до положительного числового множителя.

Обозначим через N(c) число перемен знаков в системе Штурма при x=c, при условии, что нулевые элементы этой системы вычеркнуты.

Теорема 1.5. (теорема Штурма). Если полином P(x) не имеет кратных коней и , , то число его действительных корней на интервале в точности равно числу потерянных перемен знаков в системе Штурма полинома при переходе от до , т. е.

Следствие 1. Если , то число положительных и число отрицательных корней полинома соответственно равны

Следствие 2. Для того чтобы все корни полинома P(x) степени n, не имеющего кратных корней, были действительны, необходимо и достаточно, чтобы выполнялось условие

Таким образом в уравнении (1.3) все корни будут действительными тогда и только тогда, когда:

1) система Штурма имеет максимальное число элементов n+1, т. е. m=n;

2) выполнены неравенства , т. е. старшие коэффициенты всех функций Штурма должны быть положительными.

С помощью системы Штурма можно отделять корни алгебраического уравнения, разбивая интервал (a, b), содержащий все действительные корни уравнения, на конечное число частичных интервалов таких, что

1.2.6 Теорема Бюдана–Фурье

Так как построение системы Штурма, вообще говоря, требует громоздких вычислений, то на практике ограничиваются более простыми частными приемами подсчета числа действительных корней алгебраический уравнений.

Определение. Пусть дана конечная упорядоченная система действительных чисел

, , …, , (1.10)

где и .

С одной стороны, назовем нижним числом перемен знаков системы (1.10) число перемен знаков в преобразованной системе (1.10), где нулевые элементы

(, ) заменены элементами такими, что

Очевидно, что если система (1.10) не имеет нулевых элементов, то число N перемен знаков в этой системе по смыслу совпадает с ее нижним и верхним числами перемен знаков:

вообще же говоря, .

Теорема 1.6. (теорема Бюдана–Фурье). Если числа a и b (a 0) !определение действительных корней

where (mask) eps = abs(b2/(b1(0:4)*b1(0:4))-1)

flag = maxval(eps)>epsilon! ограничение точности

if (.not. flag) then

if (.not. mask(i)) then

e1 = abs(b2(i-1) — b1(i-1)*b1(i-1))

e2 = abs(b2(i+1) — b1(i+1)*b1(i+1))

e1 = abs(b2(i-1) — b1(i-1)*b1(i-1))

e2 = abs(b2(i) — b1(i)*b1(i))

b1(0:4) = b2 !запоминаем значение коэффициентов на текущей итерации

!определение номеров комплексных корней

if (.not. mask(i)) m=i

!вычисление корней в уравнении Q(y) = 0

if (mask(i)) y(i) = b1(i)/b1(i-1)

!вычисление действительных корней

where (mask(1:4)) lg = exp(koef*log(y))

!определение знака действительных корней

where (flags) lg = -1.0*lg

!составляем уравнение для нахождения комплексных корней

Метод Лобачевского при решении алгебраических уравнений

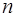
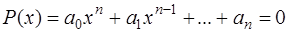
Особое место среди нелинейных уравнений занимают алгебраические уравнения или полиномы -ой степени, которые можно представить в виде:

. (7.5.16)

Для нахождения корней алгебраического уравнения можно использовать методы простой итерации и Ньютона, но, во-первых, эти методы предназначены для отыскания действительных простых корней и, во-вторых, даже если нужно найти только действительные корни необходимо для каждого корня указать интервалы, содержащие изолированные корни и определить начальные приближения.

Для нахождения корней полиномов существует метод Лобачевского. Он не требует определения начальных приближений для корней и позволяет одновременно найти все корни полинома (7.5.16). Недостатком этого метода является тот факт, что при вычислениях приходится иметь дело с числами, которые сильно различаются по порядкам величин.

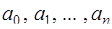
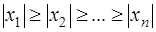
Пусть коэффициенты полинома (7.5.16) являются действительными числами, а корни пронумерованы в следующем порядке:

. (7.5.17)

Кроме того, будем предполагать, что все корни являются действительными и различными. В основание метода Лобачевского положены следующие соотношения между корнями и коэффициентами алгебраического уравнения (равенства Виетта):

(7.5.18)

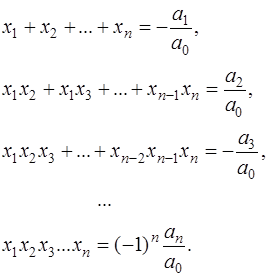
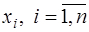
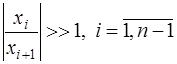
Будем говорить, что корни сильно разделены в смысле отношения их модулей, если модуль предыдущего корня во много раз больше модуля последующего корня:

. (7.5.19)

Если выполняются соотношения (7.5.19), то равенства Виетта (7.5.18) значительно упрощаются. Так, первое уравнение в (7.5.18) можно записать в виде:

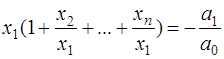
и, так как для корней выполняется соотношение (7.5.19), то все отношения, стоящие в скобках, будут величинами, пренебрежимо малыми в сравнении с единицей, и ими можно пренебречь. Тогда получим

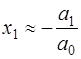
Аналогичное будет иметь место и для всех остальных равенств Виетта и (7.5.18) можно заменить следующей системой приближенных равенств, верных лишь в принятой точности вычислений:

(7.5.20)

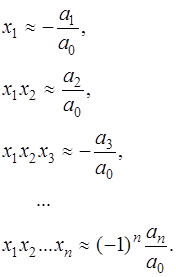
Тогда из (7.5.20) следует, что

. (7.5.21)

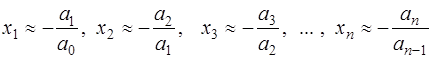
Таким образом найти сильно разделенные корни алгебраического уравнения достаточно просто. Поэтому решение уравнения (7.6.16) необходимо начинать с разделения корней. Для этого можно воспользоваться процессом квадрирования, то есть построением последовательности таких полиномов, у которых корни последующего равны квадратам соответствующих корней предыдущего. Это равносильно вычислению коэффициентов для последовательности полиномов по следующим рекуррентным формулам:

(7.5.22)

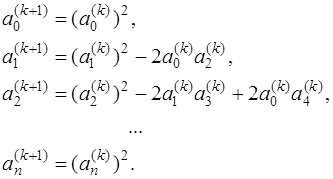
Процесс квадрирования можно прекратить, если в пределах принятой точности выполняются соотношения:

(7.5.23)

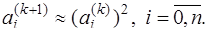
Тогда для полинома

, (7.5.24)

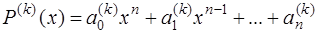
в силу разделенности его корней, выполняются соотношения аналогичные (7.5.21), а модули приближенных значений корней исходного уравнения (7.5.16) можно определить из следующих равенств:

(7.5.25)

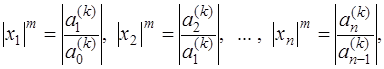
где 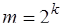, при этом знаки корней определяются подстановкой в исходное уравнение.

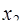
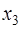
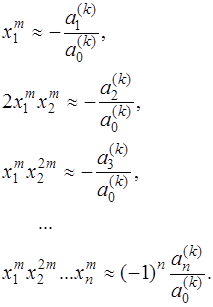
Если корни уравнения (7.5.16) все действительные и среди них есть равные по абсолютной величине, например, и , то для уравнения (7.5.24), полученного после квадрирования, будут справедливы следующие приближенные равенства:

(7.5.26)

Тогда из второго равенства в (7.5.26) следует, что

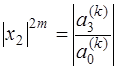
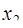
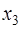
и любое из этих равенств можно использовать для определения модулей корней и , знаки которых, как и ранее, определяются подстановкой в исходное уравнение.

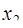
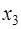
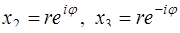
Если уравнение имеет комплексные корни, то они будут попарно сопряжены, так как все коэффициенты уравнения действительные. Пусть, например, и – пара комплексно соряженные корней. Эти корни можно представить в виде:

. (7.5.27)

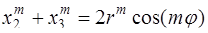
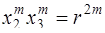
Так как и , то для уравнения (7.5.24), полученного после квадрирования, будут справедливы следующие приближенные равенства:

(7.5.28)

Тогда модуль комплексных чисел можно определить из соотношения:

, (7.5.29)

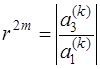
а для определения аргумента можно воспользоваться первым соотношением Виетта в (7.5.18), которое в данном случае будет иметь вид:

. (7.5.30)

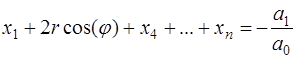
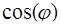
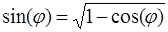
Отсюда определяется значение , а .

Таким образом, решение алгебраического уравнения методом Лобачевского осуществляется в несколько этапов.

Разделение корней путем квадрирования, при этом по поведению коэффициентов, получаемых в процессе квадрирования, делается вывод о том, какими являются корни уравнения:

· если все коэффициенты стремятся к квадратам соответствующих коэффициентов, полученных на предыдущем шаге процесса квадрирования, то все корни действительные и различные;

· если какой-то коэффициент стремится к квадрату соответствующего коэффициента, деленному на целое число, то номер этого коэффициента указывает на номер первого из равных по модулю корней уравнения в соответствии с нумерацией (7.5.17), а целое число указывает на количество таких корней;

· если какой-то коэффициент меняет знак в процессе квадрирования, то это указывает на наличие комплексно сопряженных корней, причем номер этого коэффициента указывает на первый из таких корней.

2. Вычисление значений корней по формулам, которые соответствуют сделанным выводам о виде корней.

Последнее изменение этой страницы: 2019-04-10; Просмотров: 393; Нарушение авторского права страницы

источники:

http://pandia.ru/text/78/016/14485.php

http://lektsia.com/13xa67b.html