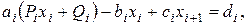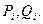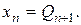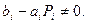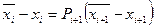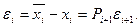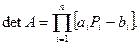Метод прогонки для уравнения с трехдиагональной матрицей

Численные методы решения линейных уравнений

Метод прогонки

Системы линейных уравнений с трехдиагональной матрицей коэффициентов при неизвестных являются наиболее важным и распространенным случаем систем специального вида. В таких системах отличны от нуля только элементы, лежащие на главной диагонали и на нижней и верхней диагоналях, прилегающих к ней. К системам с трехдиагональными матрицами приводят, например, задачи о сплайн-интерполяции, о решении разностными методами обыкновенных дифференциальных уравнений и уравнений в частных производных.

Метод прогонки принадлежит к числу прямых методов решения систем линейных уравнений и используется в тех случаях, в которых многие коэффициенты матрицы равны нулю. Это обстоятельство учтено при реализации метода прогонки, в котором исключаются преобразования с нулевыми элементами. В методе прогонки применительно к системе линейных уравнений, имеющих трехдиагональную матрицу, можно выделить следующие этапы.

• Приведение трехдиагональной матрицы к верхней треугольной (прямой ход), В случае трехдиагональной матрицы это означает приведение к двухдиагональной, т. е. приведение исходной системы к системе, содержащей по два неизвестных в каждом уравнении, кроме последнего, в котором содержится только одно неизвестное.

• Запись обратного хода в виде 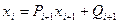, так как преобразованная матрица – двухдиагональная.

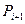
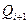
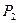
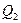
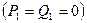
•Вывод рекуррентного соотношения для и через и и получение соотношения для и .

• Осуществление обратного хода метода прогонки и определение всех неизвестных.

Рассматриваемый метод прогонки представляет собой модификацию метода исключения Гаусса, использующую специальный регулярный вид матрицы системы. Запишем систему линейных алгебраических уравнений с трехдиагональной матрицей в виде

i = 1,2,…, n, (2.6)

Запись (2.6) представляет собой так называемый КАНОНИЧЕСКИЙ ВИД СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДА ПРОГОНКИ. При этом матрица система (2.6) имеет вид

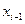
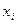
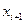
Прямой ход метода прогонки сводится к исключению неизвестного в каждом уравнении системы. Получаемая в результате прямого хода система содержит в каждом уравнении только два неизвестных и , и матрица ее – верхняя треугольная с двумя диагоналями. Запишем i-ю строку преобразованной двухдиагональной матрицы в виде

(2.7)

Если система (2.6) приведена к виду (2.7), то обратный ход метода Гаусса очевиден. Однако использование общих алгоритмов прямого и обратного хода нецелесообразно. Построим эффективную вычислительную схему, которая и составляет суть метода прогонки. Для этого, уменьшив в (2.7) индекс на единицу, запишем

Подставляя 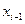в систему (2.6), получим соотношение

из которого нетрудно получить

Сравнивая это соотношение с (2.7), можем записать рекуррентные соотношения

(2.8)

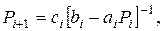
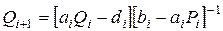
для вычисления так называемых ПРОГОНОЧНЫХ КОЭФФИЦИЕНТОВ.

Подчеркнем, что последующие значения прогоночных коэффициентов вычисляются только по известным коэффициентам системы (2.6) и известным предыдущим значениям прогоночных коэффициентов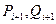

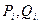
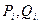
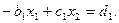
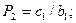
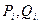
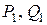
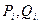
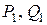
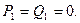
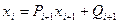
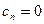
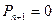
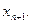
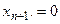
Для начала прямого хода метода прогонки необходимо задать начальные (стартовые) значения прогоночных коэффициентов, например, Отметим, что, вообще говоря, начальные значения коэффициентов в рассмотренной схеме вычислений не требуются, так как значения коэффициентов вычисляются только через коэффициенты первого уравнения системы (2.6): при i = 1 из (2.6) получаем соотношение Сравнивая это выражение с (2.7) при i =1, получаем а значение в обратном ходе вычисляем по соотношению Использование в качестве начальных значений целесообразно по двум причинам: сохраняется однородность вычислительного алгоритма для всех i = 2, 3, …,n; упрощается обсуждение и доказательство условия корректности и устойчивости метода прогонки. Из того обстоятельства, что коэффициенты не зависят от (в соотношениях(2.8) при i =1 коэффициенты умножаются на ), следует, что можно задать любые значения для прогоночных коэффициентов . Далее будет ясно, почему удобно положить Для начала обратного хода метода прогонки необходимо для вычисления задать значение . Так как , то из первого соотношения (2.8) вытекает, что и, следовательно, можно задать любое значение для Обычно полагают , и тогда

Метод прогонки устойчив, если 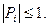Метод прогонки корректен, если

Отметим, что при устойчивости метода прогонки ошибки округления не возрастают, а подавляются. Пусть 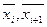— вычисленные с погрешностями значения решения. Пусть при этом коэффициенты вычисляются точно. Тогда по (2.7)

Из этой формулы при следует, что в данном случае погрешность не возрастает.

Достаточным условием корректности метода прогонки и устойчивости его к погрешностям является условие преобладания диагональных коэффициентов:

i = 1,2, …, n.

В самом деле, если хотя бы для одного значения i выполняется строгое неравенство , то можно записать цепочку неравенств:

.

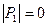
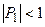
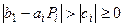
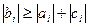
Было показано, что можно положить и тогда, во-первых, для всех i выполняется , что обеспечивает затухание погрешности, и, во-вторых, для всех i выполняется условие и, таким образом, не возникает ситуация деления на нуль. Так как условие является только достаточным, то невыполнение его не означает нарушения корректности и устойчивости.

Для реализации метода требуется примерно 8n операций, из которых 3n составляют операции типа умножения и 5n – операции типа сложения. При численном решении дифференциальных уравнений используются различные варианты метода прогонки: метод встречных прогонок, потоковая прогонка, матричная прогонка для систем векторных уравнений. Отметим, что

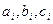
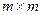
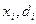
Метод прогонки обобщается на случай, при котором в системе (2.6) — квадратные матрицы размерности , а — векторы размерности m. Тогда соотношения (2.7) и (2.8) метода прогонки, в которых все действия совершаются уже над матрицами, а не над скалярами, сохраняются, а в (2.8) является соответствующей обратной матрицей.

Условие устойчивости матричной прогонки выглядит как 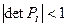, а условие корректности и устойчивости имеет вид .

Дата добавления: 2015-11-06 ; просмотров: 2632 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Метод прогонки

Метод прогонки является модификацией метода Гаусса для частного случая разреженных систем – системы уравнений с трехдиагоналъной матрицей. Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении краевых задач для дифференциальных уравнений.

Запишем систему уравнений в виде

(2.13)

На главной диагонали матрицы этой системы стоят элементы b1, b2, …, bn,над ней – элементы с1, с2. , сn-1 под ней – элементы а2, а3. , ап (при этом обычно все коэффициенты bi не равны нулю). Остальные элементы матрицы равны нулю.

Метод прогонки состоит из двух этапов – прямой прогонки (аналога прямого хода метода Гаусса) и обратной прогонки (аналога обратного хода метода Гаусса). Прямая прогонка состоит в вычислении прогоночных коэффициентов Ai,Bi,с помощью которых каждое неизвестное xi выражается через zi+1:

(2.14)

Из первого уравнения системы (2.13) найдем

С другой стороны, по формуле (2.14) Приравнивая коэффициенты в обоих выражениях для х1, получаем

(2.15)

Подставим во второе уравнение системы (2.13) вместо х1его выражение через х2по формуле (2.14):

Выразим отсюда х2 через х3:

Аналогично вычисляют прогоночные коэффициенты для любого номера i:

(2.16)

Обратная прогонка состоит в последовательном вычислении неизвестных xi. Сначала нужно найти хп. Для этого воспользуемся выражением (2.14) при i = п –1 и последним уравнением системы (2.13). Запишем их:

Отсюда, исключая хn-1, находим

Далее, используя формулы (2.14) и вычисленные ранее по формулам (2.15), (2.16) прогоночные коэффициенты, последовательно вычисляем все неизвестные хn—1, xn-2. ,х1. Алгоритм решения системы линейных уравнений вида (2.13) методом прогонки приведен на рис. 2.4.

Рис. 2.4. Алгоритм метода прогонки

При анализе алгоритма метода прогонки надо учитывать возможность деления на нуль в формулах (2.15), (2.16). Можно показать, что при выполнении условия преобладания диагональных элементов, т.е. если , причем хотя бы для одного значения iимеет место строгое неравенство, деления на нуль не возникает, и система (2.13) имеет единственное решение.

Приведенное условие преобладания диагональных элементов обеспечивает также устойчивость метода прогонки относительно погрешностей округлений. Последнее обстоятельство позволяет использовать метод прогонки для решения больших систем уравнений. Заметим, что данное условие устойчивости прогонки является достаточным, но не необходимым. В ряде случаев для хорошо обусловленных систем вида (2.13) метод прогонки оказывается устойчивым даже при нарушении условия преобладания диагональных элементов.

Линейные уравнения. Решение систем линейных уравнений. Метод прогонки.

Метод прогонки (алгоритм Томаса) используют для решения СЛУ типа Ax=F, где A — трёхдиагональная матрица. Это вариант метода последовательного исключения неизвестных.

Система уравнений Ax=F равноценна соотношению:

Метод прогонки базируется на предположении, что неизвестные, которые необходимо найти, связаны соотношением:

Выразим x_i-1 и x_i через x_i+1, подставим в уравнение, используя это соотношение, (1):

где F_i — правая часть i-го уравнения.

Это соотношение выполняется не завися от решения, если потребовать:

,

,

Получаем из 1-го уравнения:

.

После того, как нашли прогоночные коэффициенты α и β, используем уравнение (2) и получим решение системы. Причем,

.

Еще одним вариантом объяснения смысла метода прогонки является такой вариант: преобразуем уравнение (1) к равнозначному ему уравнению:

c надиагональной (наддиагональной) матрицей:

Рассчеты проводим в 2 этапа. На 1-ом этапе вычисляем компоненты матрицы C′_i и вектора F′, начиная с i=2 до i=n:

На 2-ом этапе, для i=n,n−1,…,1 вычисляем решение:

Для применимости формул метода прогонки достаточно свойства строгого диагонального преобладания у матрицы A.