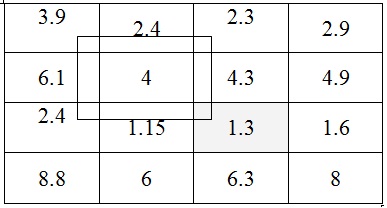
Правило прямоугольника
Алгоритм пересчета таблиц по правилу прямоугольника.
Выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Назначение сервиса . Онлайн-калькулятор Правило прямоугольника предназначен для пересчета таблиц методом жордановских преобразований.
- Шаг №1
- Шаг №2
Примечание. Данный метод не стоит путать с формулой прямоугольников.
Пример №1 . Производится пересчет элементов новой симплекс-таблицы. Каким будет значение элемента x25 в новой симплекс-таблице, если до пересчета x25 = -3 , x27 =5 , х45 = -8 , х47 =2
Пример №2 . По приведенной ниже симплекс-таблице определите, является ли соответствующее ей базисное решение оптимальным. Если решение не является оптимальным, осуществите пересчет таблицы.
| ПЧ | X3 | X4 | |
| F | -5 | 2 | -1 |
| X1 | 4 | 2 | 1 |
| X2 | 3 | 1 | 2 |
Решение.
Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных xj≥0, что эквивалентно условию неотрицательности bj≥0.
Поскольку X1 = 4 > 0, X2 = 3 > 0, то это допустимое базисное решение. Определим, является ли оно оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить. В индексной строке X4 = -1 1 /2
Следовательно, 2-ая строка является ведущей. Вместо переменной x4 в план войдет переменная x2.
Таблица 1
| ПЧ | X3 | X4 | |
| F | -5 | 2 | -1 |
| X1 | 4 | 2 | 1 |
| X2 | 3 | 1 | 2 |
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x2 , получена в результате деления всех элементов строки x на разрешающий элемент РЭ=2 (см. табл.2) . На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ
СТЭ — элемент старого плана, РЭ — разрешающий элемент (2), А и В — элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ (см. табл.2).
Формируем таблицу.
Таблица 2
| 4-(3 • 1):2 | 2-(1 • 1):2 | 1-(2 • 1):2 |
| 3 : 2 | 1 : 2 | 2 : 2 |
| -5-(3 • -1):2 | 2-(1 • -1):2 | -1-(2 • -1):2 |
Получаем новую таблицу:
Таблица 3
| ПЧ | X3 | X2 | |
| F | -3 1 /2 | 2 1 /2 | 0 |
| X1 | 2 1 /2 | 1 1 /2 | 0 |
| X4 | 1 1 /2 | 1 /2 | 1 |
Поскольку X3≥0, X2≥0, то получили оптимальный план.
Пример №3 . Решить задачу линейного программирования симплекс-методом, используя в качестве начальной угловой точки:
f(x) = -2x1 + x2 + 4x3 – x4 – x5 → min
x2 + 2x4 – x5 = 1
x1 — x4 – x5 = 1
2x2 + x3 + 2x5 = 4
xj ≥ 0, j=1. 5, x 0 = (1;1;2;0;0)
Затем систему ограничений преобразуем методом Гаусса-Жордана к такой форме, чтобы базисными стали переменные x1, x2, x3, а вектор b = (1, 1, 2) T
| -1 | 0 | -1 | 0 | -2 | 1 |
| -1 | -1 | 0 | 0 | 1 | 1 |
| -4 | 0 | -2 | -1 | 0 | -2 |
| 0 | -2 | 1 | 4 | -1 | -1 |
Итерация №1. Разрешающий элемент РЭ=-1.
Формируем таблицу.
Строка, соответствующая переменной x2 , получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую таблицу:
| -1 | 0 | -1 | 0 | -2 | 1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| -4 | 0 | -2 | -1 | 0 | -2 |
| 2 | 0 | 1 | 4 | -3 | -3 |
Итерация №2. Разрешающий элемент РЭ=-1.
Строка, соответствующая переменной x4, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x4 записываем нули.
Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую таблицу:
| -1 | 0 | -1 | 0 | -2 | 1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| 4 | 0 | 2 | 1 | 0 | 2 |
| -14 | 0 | -7 | 0 | -3 | -11 |
Итерация №3. Разрешающий элемент РЭ=-1. Строка, соответствующая переменной x3 , получена в результате деления всех элементов строки x1 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую таблицу:
| 1 | 0 | 1 | 0 | 2 | -1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| 2 | 0 | 0 | 1 | -4 | 4 |
| -7 | 0 | 0 | 0 | 11 | -18 |
Далее необходимо переназначить переменные и решать симплекс-методом.
Высшая математика и экономика
Образовательные онлайн сервисы: теория и практика
Примеры — Линейная алгебра
Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Видеоурок: Метод Жордана-Гаусса (метод прямоугольников)
Пример из видеоурока в рукописном виде:
Пример 2.
Запишем систему в виде:
4
-2
1
-2
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника: НЭ = СЭ — (А*В)/РЭ, где РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
4
-2
9
2
Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
8
2
9
4
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
8
6
4
9
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
-7.75
-12
-7.25
-2.25
Теперь исходную систему можно записать как:
x1 = -7.75 — 8×5 — 10.75×6
x2 = -12 — 10×5 — 11×6
x3 = -7.25 — 6×5 — 5.25×6
x4 = -2.25 — x5 — 1.25×6
Необходимо переменные x5,x6 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x5,x6 к 0
x1 = -7.75
x2 = -12
x3 = -7.25
x4 = -2.25
Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное.
Метод Жордана-Гаусса для решения СЛАУ
В данной статье мы рассмотрим метод Жордана-Гаусса для решения систем линейных уравнений, отличие метода Гаусса от метода Жордана-Гаусса, алгоритм действий, а также приведем примеры решений СЛАУ.
Основные понятия
Метод Жордана-Гаусса — один из методов, предназначенный для решения систем линейных алгебраических уравнений.
Этот метод является модификацией метода Гаусса — в отличие от исходного (метода Гаусса) метод Жордана-Гаусса позволяет решить СЛАУ в один этап (без использования прямого и обратного ходов).
Матричная запись СЛАУ: вместо обозначения А в методе Жордана-Гаусса для записи используют обозначение Ã — обозначение расширенной матрицы системы.
Решить СЛАУ методом Жордана-Гаусса:
4 x 1 — 7 x 2 + 8 x 3 = — 23 2 x 1 — 4 x 2 + 5 x 3 = — 13 — 3 x 1 + 11 x 2 + x 3 = 16
Записываем расширенную матрицу системы:
à = 4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16
Напоминаем, что слева от черты записывается матрица системы А :
A = 4 — 7 8 2 — 4 5 — 3 11 1
На каждом шаге решения необходимо выбирать разрешающие элементы матрицы. Процесс выбора может быть различным — в зависимости от того, как выбираются элементы, решения будут отличаться. Можно выбирать в качестве разрешающих элементов диагональные элементы матрицы, а можно выбирать произвольно.
В этой статье мы покажем оба способа решения.
Произвольный способ выбора разрешающих элементов
- Первый этап:
Следует обратиться к 1-му столбцу матрицы Ã — необходимо выбрать ненулевой (разрешающий) элемент.
В 1-ом столбце есть 3 ненулевых элемента: 4, 2, -3. Можно выбрать любой, но, по правилам, выбирается тот, чей модуль ближе всего к единице. В нашем примере таким числом является 2.
Цель: обнулить все элементы, кроме разрешающего, т.е. необходимо обнулить 4 и -3:
4 — 7 8 2 — 4 5 — 3 11 1
Произведем преобразование: необходимо сделать разрешающий элемент равным единице. Для этого делим все элементы 2-ой строки на 2. Такое преобразование имеет обозначение: I I : 2 :
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I I ÷ 2 → 4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16
Теперь обнуляем остальные элементы: 4 и -3:
4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — ( — 3 ) × I I
Необходимо выполнить преобразования:
I — 4 × I I и I I I — ( — 3 ) × I I = I I I + 3 × I I
Запись I — 4 × I I означает, что от элементов 1-ой строки вычитаются соответствующие элементы 2-ой строки, умноженные на 4.
Запись I I I + 3 × I I означает, что к элементам 3-ей строки прибавляются соответствующие элементы 2-ой строки, умноженные на 3.
I — 4 × I I = 4 — 7 8 — 23 — 4 1 — 2 5 / 2 — 13 / 2 = = 4 — 7 8 — 23 — 4 — 8 10 — 26 = 0 1 — 2 3
Записываются такие изменения следующим образом:
4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — ( — 3 ) × I I → 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2
Необходимо обнулить 2-ой столбец, следовательно, нужно выбрать разрешающий элемент: 1, -2, 5. Однако 2-ую строку матрицы мы использовали в первом этапе, так что элемент -2 не может быть использован.
Поскольку необходимо выбирать число, чей модуль ближе всего к единице, то выбор очевиден — это 1. Обнуляем остальные элементы 2-го столбца:
0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I — ( — 2 ) × I I I I — 5 × I
0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I + 2 × I I I I — 5 × I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2
Теперь требуется обнулить элементы 3-го столбца. Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37 / 2 . Обнуляем с его помощью элементы третьего столбца:
0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2
I — ( — 2 ) × I I I = I + 2 × I I I и I I — ( — 3 2 ) × I I I = I I + 3 2 × I I
получим следующий результат:
0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | — 2 0 0 1 | — 1
Ответ: x 1 = — 2 ; x 2 = 1 ; x 3 = — 1 .
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I I ÷ 2 → 4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — ( — 3 ) × I I →
→ 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I — ( — 2 ) × I I I I — 5 × I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 →
→ 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | — 2 0 0 1 | — 1 .
Выбор разрешающих элементов на главной диагонали матрицы системы
Принцип выбора разрешающих элементов строится на простом отборе соответствующих элементов: в 1-ом столбце выбирается элемент 1-го столбца, во 2-ом — второй, в 3-ем — третий и т.д.
- Первый этап
В первом столбце необходимо выбрать элемент первой строки, т.е. 4. Но поскольку в первом столбце есть число 2, чей модуль ближе к единице, чем 4, то можно поменять местами первую и вторую строку:
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 → 2 — 4 5 | — 13 4 — 7 8 | — 23 — 3 11 1 | 16
Теперь разрешающий элемент — 2. Как показано в первом способе, делим первую строку на 2, а затем обнуляем все элементы:
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I ÷ 2 → 2 — 4 5 / 2 | — 13 / 2 4 — 7 8 | — 23 — 3 11 1 | 16 I I — 4 × I I I I + 3 × I → 1 — 2 5 / 2 | — 13 / 2 0 1 — 2 | 3 0 5 17 / 2 | — 7 / 2
На втором этапе требуется обнулить элементы второго столбца. Разрешающий элемент — 1, поэтому никаких изменений производить не требуется:
0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I + 2 × I I I I I — 5 × I I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2
На третьем этапе необходимо обнулить элементы третьего столбца. Разрешающий элемент — 37/2. Делим все элементы на 37/2 (чтобы сделать равными 1), а затем обнуляем:
0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 → 1 0 — 3 / 2 | — 1 / 2 0 1 — 2 | 3 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | — 2 0 1 0 | 1 0 0 1 | — 1
Ответ: x 1 = — 2 ; x 2 = 1 ; x 3 = — 1 .
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I ÷ 2 → 2 — 4 5 / 2 | — 13 / 2 4 — 7 8 | — 23 — 3 11 1 | 16 I I — 4 × I I I I + 3 × I → 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I + 2 × I I I I I — 5 × I I →
→ 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 → 1 0 — 3 / 2 | — 1 / 2 0 1 — 2 | 3 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | — 2 0 1 0 | 1 0 0 1 | — 1
Решить СЛАУ методом Жордана-Гаусса:
3 x 1 + x 2 + 2 x 3 + 5 x 4 = — 6 3 x 1 + x 2 + 2 x 4 = — 10 6 x 1 + 4 x 2 + 11 x 3 + 11 x 4 = — 27 — 3 x 1 — 2 x 2 — 2 x 3 — 10 x 4 = 1
Записать расширенную матрицу данной системы Ã :
3 1 2 5 | — 6 3 1 0 2 | 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1
Для решения используем второй способ: выбор разрешающих элементов на главной диагонали системы. На первом этапе выбираем элемент первой строки, на втором — второй строки, на третьем — третьей и т.д.
Необходимо выбрать разрешающий элемент первой строки, т.е. 3. Затем обнуляем все элементы столбца, разделяя на 3 все элементы:
3 1 2 5 | — 6 3 1 0 2 | — 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1 I ÷ 3 → 1 1 / 3 2 / 3 5 / 3 | — 2 3 1 0 2 | — 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1 I I — 3 × I I I I — 6 × I I V + 3 × I →
→ 1 1 / 3 2 / 3 5 / 3 | — 2 0 0 — 2 — 3 | — 4 0 2 7 1 | — 15 0 — 1 0 — 5 | — 5
Необходимо обнулить элементы второго столбца. Для этого выделяем разрешающий элемент, но элемент первой строки второго столбца равен нулю, поэтому необходимо менять строки местами.
Поскольку в четвертой строке есть число -1, то меняем местами вторую и четвертую строки:
1 1 / 3 2 / 3 5 / 3 | — 2 0 0 — 2 — 3 | — 4 0 2 7 1 | — 15 0 — 1 0 — 5 | — 5 → 1 1 / 3 2 / 3 5 / 3 | — 2 0 — 1 0 — 5 | — 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4
Теперь разрешающий элемент равен -1. Делим элементы второго столбца на -1, а затем обнуляем:
1 1 / 3 2 / 3 5 / 3 | — 2 0 — 1 0 — 5 | — 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4 I I ÷ ( — 1 ) → 1 1 / 3 2 / 3 5 / 3 | — 2 0 1 0 5 | 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4 I — 1 / 3 × I I I I I — 2 × I →
→ 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 7 — 9 | — 25 0 0 — 2 — 3 | — 4
На третьем этапе необходимо также обнулить элементы третьего столбца. Для этого находим разрешающий элемент в третьей строке — это 7. Но на 7 делить неудобно, поэтому необходимо менять строки местами, чтобы разрешающий элемент стал -2:
1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 7 — 9 | — 25 0 0 — 2 — 3 | — 4 → 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 — 2 — 3 | — 4 0 0 7 — 9 | — 25
Теперь делим все элементы третьего столбца на -2 и обнуляем все элементы:
1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 — 2 — 3 | — 4 0 0 7 — 9 | — 25 I I I ÷ ( — 2 ) → 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 9 | — 25 I — 2 / 3 × I I I I V — 7 × I I I →
1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 39 / 2 | — 39
Обнуляем четвертый столбец. Разрешающий элемент — — 39 2 :
1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 39 / 2 | — 39 I V ÷ ( — 39 2 ) → 1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 1 | 2 I + I V I I — 5 × I V I I I — 3 / 2 × I V →
→ 1 0 0 0 | — 3 0 1 0 0 | — 5 0 0 1 0 | — 1 0 0 0 1 | 2 .
Ответ: x 1 = — 3 ; x 2 = — 5 ; x 3 = — 1 ; x 4 = 2
http://www.matem96.ru/primer/primer_linalgebra7.shtml
http://zaochnik.com/spravochnik/matematika/issledovanie-slau/metod-zhordana-gaussa/