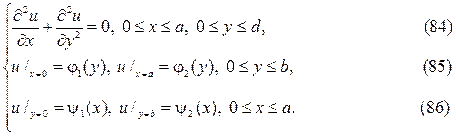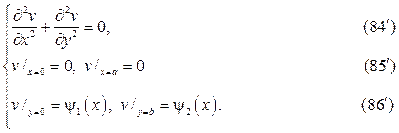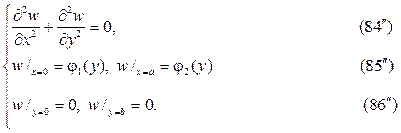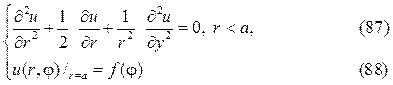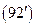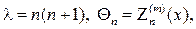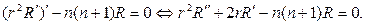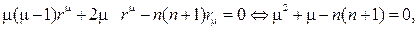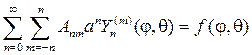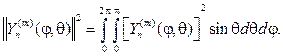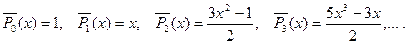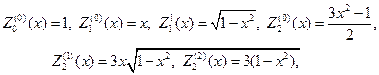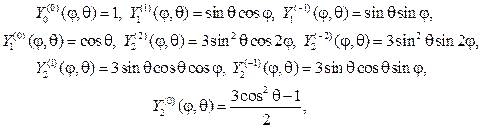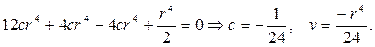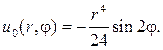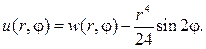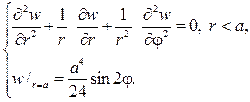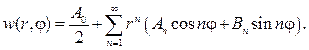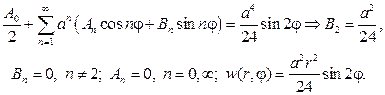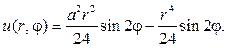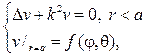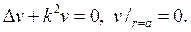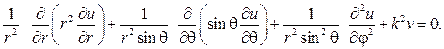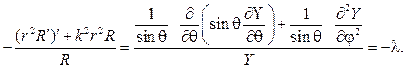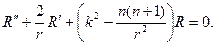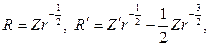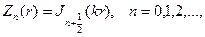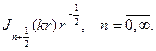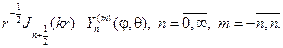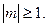МЕТОД РАЗДЕЛЕНИЯ ДЛЯ УРАВНЕНИЙ
ЭЛЛИПТИЧЕСКОГО ТИПА
Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма 
Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:
следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач
Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.
Рассмотрим задачу Дирихле для круга
где f(j)кусочно-непрерывная функция.
Следуя схеме метода Фурье полагаем
подставляем в (87) и разделяем переменные. В результате получим ра -венство
(90)
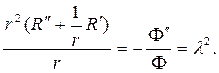
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля
откуда следует, что
(91)
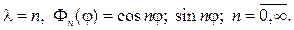
Возвращаясь к (80), решаем уравнение для радианальной функции. При
r 2 R² + rR¢ n 2 R = 0,
решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение
m(m 1)r m +m r m 
n 2 r m =0Û m 2 
n 2 =0,
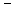
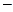
Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции
R0(r) = 1; lnr. 
С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге
Если предположить, что ряд
(93)
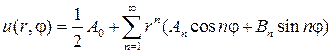
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем
(94)
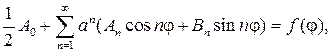
откуда с учетом формул коэффициентов Фурье следует
(95)
(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).
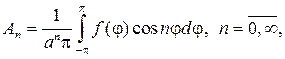
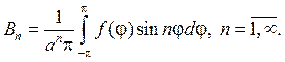
Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в
центре круга r=0.
Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом
(97)
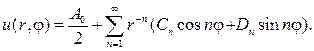
В случае кругового кольца a 2 q= 1-x 2 , найдем
(104¢)
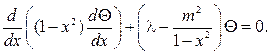
Соответственно и граничные условия (105) перейдут после замены в неравенства
(105′)
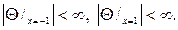
Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)
и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):
(106)
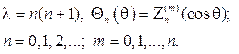
Составив произведения функций (106) на найденные выше функции Fm(j), получим множество решений уравнения (102)
(107)
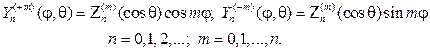
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.
Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m1¹m2 или n1¹n2
(108)
Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции
Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки
откуда находим значения m=n; (n+1) и соответственно решения
(109)
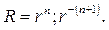
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:
Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами
(110)
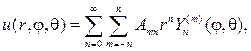
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.
Для нахождения коэффициентов Аnm подставим (110) в (100), тогда
и с учетом (108) найдем
(111)
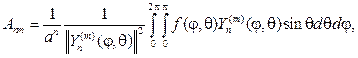
Последний интеграл вычисляется и при m=0 :
(112)
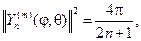
если же |m| ³ 1, то имеем
(113)
Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).
Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам
(114)
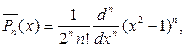
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.
(115)
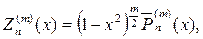
в частности будем иметь
(116)
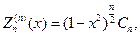
где Сn определенная константа.
С учетом (107), (115) и (116) выпишем несколько сферических функций:
(117)
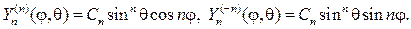
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд
(118)
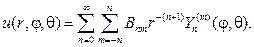
Общий вид гармонической функции в шаровом слое a 4 , и получим
Таким образом, частным решением будет функция
Вводим новую неизвестную функцию w(r,j) , полагая
Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа
Согласно (93), решение этой задачи дается формулой
Подставляя ее в граничное условие, получим
Ответом в задаче будет функция
254. Найдите решение первой краевой задачи для уравнения Гельмгольца
предполагая, что k не является собственным значением задачи
Р е ш е н и е. Запишем уравнение в сферических координатах
Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:
Функция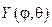 
будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l=n(n+1):
Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение
Выполняя в этом уравнении замену
придем к соотношению относительно новой функции Z(r):
Последнее уравнение в качестве ограниченных в окрестности нуля
r=0 решений имеет бесселевы функции
соответственно будем иметь набор радиальных функций
Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:
Составляем ряд с числовыми коэффициентами
(119)
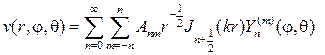
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a
где d = 4 при m = 0 и d =2 при 
При найденных коэффициентах Anm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.
255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1
Боковая панель
Полное и подробное, насколько это возможно, решение уравнения Лапласа в сферических координатах, приводящее к шаровым и сферическим функциям. Всё самое интересное на, хоть и длинной, но одной странице. Много математики — много веселья!
Эту запись можно посмотреть в nbviewer.
Уравнение Лапласа в сферических координатах
Уравнение Лапласа в сферических координатах имеет вид
где $ r, \vartheta = 90^\circ — \varphi, \lambda $ — радиус, полярное расстояние (дополнение широты $\varphi$ до $90^\circ$), долгота соответственно.
Решить уравнение Лапласа это значит найти конкретный вид гармонической функции $f \left( r, \vartheta, \lambda \right)$, удовлетворяющей ему.
Прежде, чем переходить к решению, заметим важное и полезное свойство уравнения Лапласа: оно линейно. Это означает, что если есть два решения этого уравнения $f_1$ и $f_2$, то есть
$$ \Delta f_1 = 0,\qquad \Delta f_2 = 0, $$
то их линейная комбинация
$$ f = \alpha f_1 + \beta f_2 $$
тоже является решением $\Delta f = 0$.
Разделение переменных
Будем искать решение уравнения Лапласа методом разделения переменных, суть которого в следующем. Представим искомую функцию $f$ трёх переменных $r, \vartheta, \lambda$ как произведение трёх других функций
\begin
каждая из которых теперь зависит только от одной переменной: $R$ есть функция только от $r$, $\Theta$ есть функция только от $\vartheta$, а $\Lambda$ есть функция только от $\lambda$. Стоит заметить, что не всякая система координат позволяет решить уравнение Лапласа методом разделения переменных, например этого нельзя сделать в геодезических координатах $H, B, L$.
Итак, делаем подстановку
Замечаем, что частные производные заменены на полные дифференциалы, поскольку функции $R, \Theta, \Lambda$ имеют только одну переменную. Разделим обе части уравнения на $R\Theta\Lambda$ и умножим на $r^2$:
Первый член уравнения зависит только от $r$, а вся оставшаяся часть зависит только от угловых величин $\vartheta, \lambda$. Для того, чтобы равенство выполнялось необходимо, чтобы обе части равнялись некоторой постоянной $\alpha$:
Первое уравнение будем называть радиальной частью уравнения Лапласа, поскольку она зависит только от $r$. Оставшуюся часть умножим на $\sin^<2><\left(\vartheta \right)>$ и запишем уравнение
которое является угловой частью уравнения Лапласа и называется дифференциальным уравнением сферических функций, поскольку, как увидим позже, именно они будут его решением.
И снова становится очевидным, что для сохранения равенства в полученном уравнении необходимо, чтобы обе части равнялись некоторой постоянной $\beta$:
Таким образом, уравнение Лапласа, дифференциальное уравнение в частных производных второго порядка, разбивается на три обыкновенных дифференциальных уравнения второго порядка:
$$ \begin
Отметим, что угловая часть уравнения Лапласа $Y (\vartheta, \lambda) = \Theta (\vartheta) \Lambda (\lambda)$ зависит только от полярного расстояния $\vartheta$ и долготы $\lambda$, то есть явялется функцией, заданной на сфере, следовательно решение этой части должно быть периодическим: $\pi$ для широтной части и $2\pi$ для долготной части. Только при этих условиях функция $Y (\vartheta, \lambda)$ может быть однозначно заданной на сфере.
Уравнение гармонических колебаний
Обыкновенное дифференциальное уравнение второго порядка вида
называется уравнением гармонических (или свободных) колебаний.
Оно имеет два линейно независимых решения при $\beta > 0$
что легко проверяется подстановкой.
Как уже было сказано выше, для того, чтобы функция $Y \left( \vartheta, \lambda \right)$ была однозначной на сфере, необходимо, чтобы функция $\Lambda$ имела период $2\pi$. Из последнего уравнения нетрудно установить, что такое возможно только при $\beta = m^2$, $m = 0, 1, 2, …$ Таким образом, решения уравнения гармонических колебаний принимают вид
линейная комбинация которых
является общим решением дифференциального уравнения. Здесь $C_1$ и $C_2$ — произвольные константы.
Присоединённое уравнение Лежандра
Перепишем второе уравнение, подставив в него значение $\beta = m^2$:
И подставляя всё это, получим уравнение без тригонометрических функций в явном виде:
$$ \left( 1 — t^2 \right) \dfrac
Сначала установим некоторые свойства решения этого уравнения.
- Во-первых, поскольку $t = \cos<\vartheta>$, то $-1 \leq t \leq +1$. Таким образом, областью определения $P (t)$ является интервал $[-1, 1]$.
- Во-вторых, поскольку $0 \leq \vartheta \leq \pi$ и $-1 \leq t \leq +1$, то по теорема Вейерштрасса функция $P (t)$ является ограниченной и должна принимать некоторые конечные значения на этом интервале:
$$ \left|P (-1)\right| Сферические функции
Пользуясь полученными нами решениями уравнения гармонических колебаний и присоединённого уравнения Лежандра, мы можем записать теперь решение дифференциального уравнения для сферических функций (или угловой части уравнения Лапласа) в виде:
$$ Y_n^m \left( \vartheta, \lambda \right) = P_n^m (\cos<\vartheta>) \cos
Функции такого вида называют элементарными сферическими функциями степени $n$ и порядка $m$. Видно, что степень и порядок элементарной сферической функции определяется степенью и порядком присоединённой функции Лежандра.
Поскольку дифференциальное уравнение для сферических функций является линейным, то и линейная комбинация его решений также будет решением. Эту комбинацию можно записать как
где $A_n^m$ и $B_n^m$ являются произвольными константами, которые ещё называют гармоническими коэффициентами или просто гармониками. Мы получили общее выражение для сферической функции степени $n$.
Уравнение Коши-Эйлера
Наконец, найдём решение радиальной части уравнения Лапласа. Запишем её снова:
\begin
Это уравнение Коши—Эйлера — линейное дифференциальное уравнение второго порядка с переменными коэффициентами. Будем искать решение в виде степенной функции $R = r^n$, тогда
Подставляем в дифференциальное уравнение и после тривиальных преобразований, получаем
\begin
Сокращаем на $r^n$, получаем характеристическое уравнение
\begin
два корня которого легко находим из решения квадратного уравнения
откуда, возвращаясь к нашей подстановке $R = r^n$, получаем два линейно независимых решения
Теперь, пользуясь значением для $\alpha = n (n + 1)$, которое мы установили выше при рассмотрении присоединённого уравнения Лежандра, находим решения
линейная комбинация которых
по свойству линейных ОДУ второго порядка, является общим решением дифференциального уравнения. Здесь $C_1, C_2$ — произвольные постоянные.
Таким образом, мы получили решение радиальной (зависимой только от $r$) части уравнения Лапласа.
Шаровые функции
Итак, мы решили все обыкновенные дифференциальные уравнения, возникшие после разделения переменных в уравнении Лапласа в сферических координатах. Осталось найти окончательный вид решения. Напоминаю, что искали мы его в виде
\begin
Подставляем сюда выражения \eqref
\begin
которые называются шаровыми функциями (solid spherical harmonics), а функции $Y (\vartheta, \lambda)$ — сферическими (spherical harmonics). Таким образом, последние два выражения устанавливают связь шаровых и сферических функций.
Используя общее выражение для сферической функции степени $n$ \eqref
\begin
Вспоминая свойство линейности, о котором мы упоминали в самом начале, можно записать общее решение уравнения Лапласа, как линейную комбинацию частных решений в виде ряда по степеням $n$:
\begin
Эти выражения называются рядами шаровых функций, а при $r = 1$ они обратятся в ряды сферических функций или ряды Лапласа.
Ряды шаровых функций и являются решением уравнения Лапласа в сферических координатах.
Для геодезии, изучающей внешнее гравитационное поле, куда более важными являются шаровые функции вида $f = r^ <-n-1>Y_n (\vartheta, \lambda)$, через которые может быть выражен потенциал притяжения вне притягивающих масс, поскольку $r$ здесь, как и у потенциала притяжения стоит в знаменателе. Вообще говоря, любая гармоническая вне сферы функция $f_e$ ($e$, external) может быть разложена в ряд
$$ f_e = \sum\limits_
а любая гармоническая внутри сферы функция $f_i$ ($i$, internal) может быть разложена в ряд
$$ f_i = \sum\limits_
http://thegeodesy.com/solving-laplace-equation/