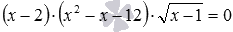Метод разложения на множители иррациональных уравнений

Метод разложения на множители при решении иррациональных уравнений

Продолжаем знакомиться с методами решения иррациональных уравнений. В этой статье мы детально разберем, как используется метод разложения на множители при решении иррациональных уравнений. Материал представим так: кратко напомним основные положения метода, после чего будем подробно разбирать решения характерных иррациональных уравнений методом разложения на множители.

Основные положения метода разложения на множители

В статье метод разложения на множители очень подробно разобрана вся соответтвующая теория. Здесь мы не будем ее полностью повторять, а перечислим лишь основные положения и запишем алгоритм метода разложения на множители. Просто удобно, если он будет перед глазами, когда мы перейдем к решению примеров.

Метод разложения на множители применяется для решения уравнений, в левых частях которых находится некоторое произведение, а в правых – нули, то есть, для решения уравнений вида f₁(x)·f₂(x)·…·f_n(x)=0 , где f₁, f₂, …, f_n – некоторые функции. Суть метода состоит в замене уравнения f₁(x)·f₂(x)·…·f_n(x)=0 совокупностью уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 на ОДЗ переменной x для исходного уравнения.

Первая часть последнего предложения про переход к совокупности следует из известного с начальной школы факта: произведение нескольких чисел тогда и только тогда равно нулю, когда хотя бы одно из чисел равно нулю. Наличие второй части про ОДЗ объясняется тем, что переход от уравнения f₁(x)·f₂(x)·…·f_n(x)=0 к совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 может быть неравносильным и приводить к появлению посторонних корней, от которых в данном случае позволяет избавиться учет ОДЗ. Стоит отметить, что отсеивание посторонних корней, если это удобно, может быть проведено не только через ОДЗ, но и другими способами, например, проверкой через подстановку найденных корней в исходное уравнение.

Итак, чтобы решить уравнение f₁(x)·f₂(x)·…·f_n(x)=0 методом разложения на множители, в том числе и иррациональное, нужно

• Перейти к совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 ,
• Решить составленную совокупность,
• Если совокупность решений не имеет, то сделать вывод об отсутствии корней у исходного уравнения. Если же корни есть, то отсеять посторонние корни.

Переходим к практической части.

Примеры решения характерных иррациональных уравнений

Левые части типичных иррациональных уравнений, которые решаются методом разложения на множители, представляют собой произведения нескольких алгебраических выражений, обычно линейных двучленов и квадратных трехчленов, и нескольких корней с алгебраическими выражениями под ними. В правых частях нули. Такие уравнения идеальны для получения начальных навыков использования метода разложения на множители для решения иррациональных уравнений. С решения подобного уравнения начнем и мы. При этом попробуем достичь двух целей:

• разобрать все шаги алгоритма,
• вспомнить три основных способа отсеивания посторонних корней (по ОДЗ, по условиям ОДЗ и при помощи непосредственной подстановки решений в исходное уравнение).

Решить иррациональное уравнение

Следующее иррациональное уравнение 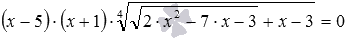типично в том плане, что при его решении методом разложения на множители отсеивание посторонних корней удобно проводить по условиям ОДЗ, а не по ОДЗ в виде числового множества, так как получить ОДЗ в виде числового множителя затруднительно. Сложность в том, что одно из условий, определяющих ОДЗ, представляет собой иррациональное неравенство . Указанный подход к отсеиванию посторонних корней позволяет обойтись без его решения, более того, иногда в школьном курсе математики вообще не знакомятся с решением иррациональных неравенств.

Решить уравнение

Хорошо, когда уравнение имеет в левой части произведение, а в правой – ноль. В этом случае сразу можно переходить к совокупности уравнений, решить ее, найти и отбросить посторонние для исходного уравнения корни, что даст искомое решение. Но чаще уравнения имеют иной вид. Если при этом просматривается возможность преобразовать их к виду, подходящему для применения метода разложения на множители, то почему бы не попробовать провести соответствующие преобразования. Например, чтобы получить произведение в левой части следующего иррационального уравнения, достаточно прибегнуть к формуле сокращенного умножения разность квадратов.

Решить иррациональное уравнение

Есть еще один класс уравнений, которые обычно решают методом разложения на множители. К нему относятся уравнения, обе части которых являются произведениями, имеющими одинаковый множитель в виде выражения с переменной. Таково, например, иррациональное уравнение . Можно пойти путем деления обеих частей уравнения на одинаковый множитель, но при этом нельзя забывать отдельно проверять значения, обращающие в нуль это выражения, иначе можно потерять решения, ведь деление обеих частей уравнения на одно и то же выражение может быть неравносильным преобразованием. Надежнее действовать по методу разложения на множители, это позволяет гарантированно избежать потери корней при дальнейшем корректном решении. Понятно, что для этого надо сначала получить в левой части уравнения произведение, а в правой части получить ноль. Это легко: достаточно перенести выражение из правой части в левую, изменив его знак, и вынести общий множитель за скобки. Покажем полное решение подобного, но чуть более сложного иррационального уравнения.

Решить уравнение

Решение любого уравнения (как, впрочем, и решение многих других задач) полезно начинать с нахождения ОДЗ, особенно если ОДЗ находится легко. Приведем несколько самых очевидных доводов в пользу этого.

• Довольно часто требуется проводить какие-либо преобразования уравнения (как, например, в предыдущем примере), а они, как известно, проводятся на ОДЗ.
• Во многих случаях так и так приходится находить ОДЗ, так как это является неотъемлемой частью алгоритма выбранного метода решения, так почему бы не найти ОДЗ сразу. Например, последний шаг алгоритма метода разложения на множители состоит в отсеивании посторонних корней, что удобно делать, используя ОДЗ.
• А иногда ОДЗ позволяет сразу сделать вывод об отсутствии корней или ограничить круг поиска корней несколькими числами. Это относится к случаям, когда ОДЗ есть пустое множество или множество, представляющее собой некоторое количество чисел. Подробнее об этом поговорим в отдельной статье решение иррациональных уравнений через ОДЗ.

Итак, получив задание решить уравнение, не стоит без оглядки бросаться в преобразования-вычисления, может достаточно взглянуть на ОДЗ? Это ярко демонстрирует следующее иррациональное уравнение.

Решите иррациональное уравнение

На этом можно считать, что мы освоили решение иррациональных уравнений методом разложения на множители. Можно двигаться дальше: начинать разбирать графический метод решения иррациональных уравнений.

Конспект урока «Решение иррациональных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Урок алгебра 11 класс Михальчук Н.Л. учитель математики НИСЦ РО «Восток» для одаренных детей

Тема: Решение иррациональных уравнений

Цель: обеспечение качества усвоения учащимися образовательного стандарта по теме «Решение иррациональных уравнений».

рассмотреть понятие «иррациональное уравнение»;

рассмотреть основные и дополнительные методы решения иррациональных
уравнений;

способствовать сознательному усвоению учащимися способов решения
иррациональных уравнений.

Организационный момент (2 мин) Приветствие

Вашему вниманию предлагаем урок-лекцию по теме «Решение иррациональных уравнений», предназначенную для изучения учащимися 9-10 классов и для обобщения, дополнительного осмысления и обогащения знаний учащимися 11 классов. Решение иррациональных уравнений, по мнению учащихся и педагогов обычно вызывает затруднения. Обращение к данной теме при подготовке к ЕНТ, поступлению ВУЗы является актуальным и целесообразным. Во время занятия мы рассмотрим не только основные методы решения иррациональных уравнений, но и дополнительные. Прежде, чем рассмотреть способы и приемы решения данных уравнений, обратимся к определению иррационального уравнения.

Определение: Иррациональным уравнением называется уравнение, содержащее неизвестную под знаком радикала, а также под знаком возведения в дробную степень.

Основная цель при решении иррациональных уравнений состоит в том, чтобы освободиться от знака радикала и получить рациональное уравнение.

При решении иррациональных уравнений применяют следующие основные методы: • возведение в степень обеих частей уравнения;

введение новой переменной;

разложение на множители.

Кроме основных методов следует рассмотреть дополнительные методы решения иррациональных уравнений:

умножение на сопряженное;

переход к уравнению с модулем;

метод «пристального взгляда» (метод анализа уравнения);

использование монотонности функции.

Прежде чем приступить к решению иррационального уравнения, используя вышеперечисленные методы, необходимо обратить внимание на вид данного уравнения. Это позволяет определить, есть ли смысл решать уравнение вообще, и если да, то каким способом его можно решить.

К примеру, нет смысла приступать к решению уравнения

арифметического корня не может быть отрицательным числом.

Рассмотрим каждый из основных методов.

а) если иррациональное уравнение содержит только один радикал, то нужно
записать так, чтобы в одной части знака равенства оказался только этот радикал.
Затем обе части уравнения возводят в одну и ту же степень, чтобы получилось
рациональное уравнение;

б) если в иррациональном уравнении содержится два или более радикала, то
сначала изолируется один из радикалов, затем обе части уравнения возводят в
одну и ту же степень, и повторяют операцию возведения в степень до тех пор,
пока не получится рациональное уравнение.

3) При возведении обеих частей уравнения в одну и ту же степень получается уравнение, не равносильное данному. Поэтому необходимо проверить, удовлетворяют или не удовлетворяют найденные значения переменной данному уравнению. Проверка является составной частью решения иррациональных уравнений, целью которой является исключение посторонних корней уравнения.

В данном случае проверка оказалась довольно простой. Но могут встретиться уравнения, корни которых иррациональны, и проверка приводит к очень сложным вычислениям. В таких случаях лучше решать простейшие иррациональные уравнения с помощью равносильных преобразований по следующей схеме:

Методы решения иррациональных уравнений

Методы решения иррациональных уравнений.

Цели:

Образовательная –познакомить учащихся с нестандартными методами решения иррациональных уравнений; систематизировать знания учащихся о методах решения иррациональных уравнений, способствовать формированию умений классифицировать иррациональные уравнения по методам решений, научить применять эти методы, выбирать рациональный путь решения. Развивающая –способствовать развитию математического кругозора, логического мышления. Воспитательная – содействовать воспитанию интереса к иррациональным уравнениям, воспитывать чувство коллективизма, самоконтроля, ответственности.

1. Повторить определение и основные методы решения иррациональных уравнений;

2. Продемонстрировать нестандартные методы решения иррациональных уравнений; формировать умение выбирать рациональные пути решения;

3. Освоение всеми учащимися алгоритмов решения иррациональных уравнений, закрепление теоретических знаний при решении конкретных примеров;

4. Развитие у учащихся логического мышления в процессе поиска рациональных методов и алгоритмов решения;

5. Развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.

Тип урока: комбинированный

Методы обучения:

Информационно- иллюстративный; репродуктивный; проблемный диалог; частично-поисковый; системные обобщения.

Формы организации учебной деятельности:

Фронтальная, групповая, самопроверка, взаимопроверка, коллективные способы обучения.

Оборудование урока: компьютер, проектор, карточки с заданием, лист учета знаний.

Продолжительность занятия: 2 урока по 45 минут.

План урока:

I. Организационный момент. Постановка цели, мотивация.

II. Актуализация опорных знаний, проверка домашней работы.

III. Изучение нового материала.

IV. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

V. Подведение итогов и результатов урока. Рефлексия.

VI. Задание на дом.

I Организационный момент. Постановка цели, мотивация.

II Актуализация опорных знаний проводится в форме беседы по лекционному материалу по данной теме с использованием компьютерной презентации. Проверка домашнего задания.

· Определение иррационального уравнения.

Уравнение, содержащее переменные под знаком корня или дробной степени, называется иррациональным.

Назовите иррациональные уравнения:

· Что значит решить иррациональное уравнение?

Это значит найти все такие значения переменной, при которых уравнение превращается в верное равенство, либо доказать, что таких значений не существует.

· Основные методы решения иррациональных уравнений.

1. Уединение радикала. Возведение в степень.

a) При решении иррационального уравнения с радикалом четной степени возможны два пути:

1) использование равносильных преобразований

для уравнения вида

для уравнения вида

2) после возведения в степень выполнение проверки, так как возможно появление посторонних корней

b) При решении иррационального уравнения с радикалом нечетной степени возведение в нечетную степень правой и левой части уравнения всегда приводит к равносильному уравнению и потеря корней или их приобретения происходить не может.

Пример 1:

Пример 2:

Пример 3:

Проверка: x=2 x=5

— посторонний корень

Если радикалов несколько, то уравнение возводить в степень приходится возводить неоднократно.

Пример 4:

Проверка показывает, что оба корня подходят.

Ответ:

2. Метод введения вспомогательного неизвестного или “метод замены

Пример 5:

Сделаем замену причём тогда

не удовлетворяет условию

Возвращаемся к замене:

Проверка показывает, что оба корня подходят.

Иногда удобно ввести не одну, а несколько переменных.

Пример 6: .

Заметим, что знаки х под радикалом различные. Введем обозначение

, .

Тогда,

Выполним почленное сложение обеих частей уравнения .

Имеем систему уравнений

Т. к. а + в = 4, то

Значит: 9 – x = 8 , х = 1.

3. Метод разложения на множители или расщепления.

· Произведение равно нулю тогда и только тогда, когда хотя бы один из входящих в него сомножителей равен нулю, а остальные при этом имеют смысл.

Пример 7:

III Изучение нового материала.

Нестандартные методы решения иррациональных уравнений.

4. Умножение на сопряжённое выражение.

5. Переход к модулю.

6. Использование свойств функции:

§ Область определения функции (ОДЗ)

§ Область значения функции

§ Свойство ограниченности функции (метод оценок)

§ Использование суперпозиций функций

· Умножение на сопряжённое выражение.

Воспользуемся формулой

Пример 8:

Умножим обе части уравнения на сопряжённое выражение:

Проверка показывает, что число является корнем.

Ответ:

· Переход к модулю.

Для этого метода воспользуемся тождеством:

Пример 9:

§ Если , то , тогда

тогда

§ Если , тогда ,а

§ Если , тогда , а

· Использование свойств функции:

§ Область определения функции (ОДЗ)

Иногда нахождение области определения функций, входящих в уравнение, существенно облегчает его решение.

Пример 10:

ОДЗ: ОДЗ: x=0 и x=1

Проверка показывает, что только x=1 является корнем.

Ответ:

Пример 11:

, тогда

Тогда невозможно.

Ответ: корней нет.

§ Область значений функции

Пример 12:

Данное уравнение не имеет решений, так как его левая часть — функция может принимать только неотрицательные значения.

Ответ: корней нет

Пример 13:

Учитывая то, что левая часть уравнения – функция может принимать только неотрицательные значения, решим неравенство:

неравенство решений не имеет, тогда и исходное уравнение тоже.

Ответ: корней нет

§ Свойство ограниченности функции (метод оценок)

· Если и , то

Пример 14:

Заметим, что , т. е. , а

Проверка показывает, что это значение является и корнем второго уравнения.

Ответ:

· Пусть — функция, возрастающая (убывающая) на некотором промежутке I. Тогда уравнение имеет на промежутке I не более одного корня.

· Пусть — функция, возрастающая на некотором промежутке I , а функция — убывающая на этом промежутке. Тогда уравнение имеет на промежутке I. не более одного корня

Пример 15: .

Рассмотрим функции и .

монотонно возрастает, а — убывает, следовательно, уравнение имеет не более одного корня.

Значение корня легко найти подбором:

Ответ:

Пример 16:

Функция возрастает на своей области определения, как сумма двух возрастающих функций, следовательно, уравнение имеет не более одного корня. Так как , то — единственный корень .

Ответ:

§ Использование суперпозиций функций

· Если — монотонно возрастающая функция, то уравнения и равносильны.

Пример 17:

Запишем уравнение в виде

Рассмотрим функцию — монотонно возрастающую, тогда уравнение имеет вид . Оно равносильно уравнению

Сделаем замену

не удовлетворяет условию

Ответ:

IV. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

Решение уравнений в группах по 6 человек.

Ребята получают карточку с заданием. Решение уравнений обсуждают вместе, записывают его.

После выполнения группами заданий проводится взаимопроверка. Группы меняются заданиями с решениями по кругу:

2 3 4

Учащиеся групп обсуждают решение, исправляют ошибки и выставляют оценки.

Потом работы с выставленными оценками возвращаются в группы для обсуждения вклада каждого в решение проблемы.

Выставляются каждому оценки с занесением в оценочную таблицу. Учитель контролирует и вносит, если нужно, свои коррективы.

V. Подведение итогов и результатов урока. Рефлексия.

1)

2)

3)

4)

5)

6)

7)

8) *

Используемая литература.

1. Чулков курса «Уравнения и неравенства в школьном курсе математики»: Лекции 1-8. – М.: Педагогический университет «Первое сентября», 2006.

2. , , Морозова государственный экзамен. Математика. – Челябинск: Взгляд, 2006 –Ч.1,2

3. Шарыгин курс по математике: Решение задач. – М.: Просвещение, 1989

4. , Якушев : интенсивный курс подготовки к экзамену. – М.: Айрис-пресс, 2004.

5. , Голобородько и контрольные работы по алгебре и началам анализа для 10-11 классов. – М.: Илекса, 2006.

Задания для работы в группах:

1. Возведи обе части в квадрат:

2. Выполни замену:

4. Умножай на сопряжённое выражение:

5. Переходи к модулю:

6. Используй свойства функций:

7. Реши любым способом:

1. Возведи обе части в квадрат:

2. Выполни замену:

4. Умножай на сопряжённое выражение:

5. Переходи к модулю:

6. Используй свойства функций:

7. Реши любым способом:

Проверочная работа по теме: «Методы