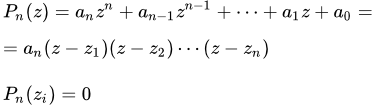Метод разложения на множители рациональных уравнений

Решение уравнений методом разложения на множители

Решение уравнений разложения на множители (метод расщепления) – это способ решения уравнений при котором мы стремимся уравнение свести их к виду:

а затем каждую скобку приравнять к нулю и решить как отдельное уравнение.

Вынесем за скобку икс.

Разобьем уравнение на два простейших.

В первом корень уравнения уже понятен, во втором надо перенести \(5\) в правую сторону.

Решение методом разложения на множители основывается на простой идее:

В результате умножения ноль можно получить, только если один из множителей равен нулю.

Попробуйте придумать два числа, которые при умножении дают ноль. Вы убедитесь, что хотя бы одно из них обязательно должно быть нулем.

Этот метод решения уравнений один из самых популярных, поэтому освоить его очень важно для тех, кто планирует иметь четверки и пятерки. А для освоения этого метода, конечно, надо уметь раскладывать на множители как Бог: знать все формулы сокращенного умножения, легко выносить множители за скобки, уметь применять метод группировки и т.д. Подробнее о всех способах разложения на множители смотри здесь .

Пример(задание из ОГЭ). Решите уравнение \(x^3+4x^2-4x-16=0\).
Решение:

Перед нами кубическое уравнение.
Применим метод группировки: из первой пары слагаемых вынесем \(x^2\), а из второй – минус четверку.

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №12. Решение алгебраических уравнений разложением на множители.

Перечень вопросов, рассматриваемых в теме

1) типы алгебраических уравнений;

2) решение алгебраические уравнения методом разложения на множители;

3) методы решения алгебраических уравнений.

Глоссарий по теме

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Биквадратными называются уравнения вида ах 4 + bх 2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Симметрическим уравнением 3-ей степени называют уравнение вида: ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.

Уравнение вида a n x n ₊a n-1 x n-1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a n-1 =a k , при k=0, 1, …, n.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Давайте вспомним, что такое алгебраическое уравнение?

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над полем F.

Степенью алгебраического уравнения называют степень многочлена P.

является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.

Связанные определения. Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Примеры и разбор решения заданий тренировочного модуля

1. Алгебраические уравнения, решаемые разложением на множители:

D(–2) : ,

Можно догадаться, что число х₁ = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.

х + 1 = 0 или х 2 –х–2 = 0;

х₁ = –1 х_2,3 = ;

х_2,3 = ;

x 3 + х 2 – х 2 – х – 2x – 2 = 0;

(x 3 + х 2 ) – (х 2 + х) – 2(x + 1) = 0;

х 2 (х + 1) – х(х + 1) – 2(х + 1) = 0;

(х + 1) (х + 1) (х –2) = 0;

(х –2) = 0;

1. Уравнения, сводящиеся к алгебраическим
   1. Биквадратные уравнения

На прошлом уроке мы познакомились с данным видом уравнений

Определение. Биквадратными называются уравнения вида ах 4 + bх 2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Метод решения

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х 2 .

Новое квадратное уравнение относительно переменной у: ay 2 +by+c=0.

Решая это уравнение, мы получаем корни квадратного уравнения

Решая эти два уравнения (y₁=x₁ 2 и y₂=x₁ 2 ) относительно переменной x, мы получаем корни данного биквадратного уравнения.

Порядок действий при решении биквадратных уравнений

1. Ввести новую переменную у=х 2
2. Подставить данную переменную в исходное уравнение
3. Решить квадратное уравнение относительно новой переменной
4. После нахождения корней (y₁; y₂) подставить их в нашу переменную у=х 2 и найти исходные корни биквадратного уравнения

х 4 – 8х 2 – 9 = 0.

Решение: Пусть у = х 2 , где у 0; у 2 – 8у – 9 = 0;

По формулам Виета:

Первое решение отбрасываем ( у 0),

а из второго находим х₁ = –3; х₂ = 3.

2 Симметрические уравнения

Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.

Симметрическим уравнением 3-ей степени называют уравнение вида ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.

Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:

1 0 . У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.

Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х 3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е.

(х + 1)(ах 2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах 2 + (b – а)x + а = 0,

первое уравнение и доказывает интересующее нас утверждение.

2 0 . У симметрического уравнения корней, равных нулю, нет.

3 0 . При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.

х 3 + 2x 2 + 2х + 1 = 0.

Решение: У исходного уравнения обязательно есть корень х = –1.

Разлагая далее левую часть на множители, получим

(х + 1)(x 2 + х + 1) = 0.

x 2 + х + 1 = 0 не имеет корней.

2 Возвратные уравнения

Уравнение вида a n x n ₊a n-1 x n-1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a n-1 =a k , при k=0, 1, …, n.

Рассмотрим возвратное уравнение четвёртой степени вида

ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.

Порядок действий при решении возвратных уравнений вида ax 4 + bx 3 + cx 2 + bx + a = 0:

• разделить левую и правую части уравнения на . При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
• группировкой привести полученное уравнение к виду

• ввести новую переменную , тогда выполнено
  , то есть ;

в новых переменных рассматриваемое уравнение является квадратным: at 2 +bt+c–2a=0;

• решить его относительно t, возвратиться к исходной переменной.

Решение: Разделим на x 2 , получим:

Введем замену:
Пусть

Методы разложения многочленов на множители

Основа метода

Пусть

– многочлен степени n ≥ 1 от действительной или комплексной переменной z с действительными или комплексными коэффициентами a_i . Примем без доказательства следующую теорему.

Теорема 1

Уравнение P_n ( z ) = 0 имеет хотя бы один корень.

Докажем следующую лемму.

Лемма 1

Пусть P_n ( z ) – многочлен степени n , z ₁ – корень уравнения:
P_n ( z ₁) = 0 .
Тогда P_n ( z ) можно представить единственным способом в виде:
P_n ( z ) = ( z – z ₁) P_{n– 1} ( z ) ,
где P_{n– 1} ( z ) – многочлен степени n – 1 .

Доказательство

Для доказательства, применим теорему (см. Деление и умножение многочлена на многочлен уголком и столбиком), согласно которой для любых двух многочленов P_n ( z ) и Q_k ( z ) , степеней n и k , причем n ≥ k , существует единственное представление в виде:
P_n ( z ) = P_n–k ( z ) Q_k ( z ) + U_{k– 1} ( z ) ,
где P_n–k ( z ) – многочлен степени n–k , U_{k– 1} ( z ) – многочлен степени не выше k– 1 .

Положим k = 1 , Q_k ( z ) = z – z ₁ , тогда
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) + c ,
где c – постоянная. Подставим сюда z = z ₁ и учтем, что P_n ( z ₁) = 0 :
P_n ( z ₁ ) = ( z ₁ – z ₁ ) P_{n– 1} ( z ₁ ) + c ;
0 = 0 + c .
Отсюда c = 0 . Тогда
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) ,
что и требовалось доказать.

Разложение многочлена на множители

Итак, на основании теоремы 1, многочлен P_n ( z ) имеет хотя бы один корень. Обозначим его как z ₁ , P_n ( z ₁ ) = 0 . Тогда на основании леммы 1:
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) .
Далее, если n > 1 , то многочлен P_{n– 1} ( z ) также имеет хотя бы один корень, который обозначим как z ₂ , P_{n– 1} ( z ₂ ) = 0 . Тогда
P_{n– 1} ( z ) = ( z – z ₂ ) P_{n– 2} ( z ) ;
P_n ( z ) = ( z – z ₁ )( z – z ₂ ) P_{n– 2} ( z ) .

Продолжая этот процесс, мы приходим к выводу, что существует n чисел z ₁ , z ₂ , . , z _n таких, что
P_n ( z ) = ( z – z ₁ )( z – z ₂ ) . ( z – z _n ) P ₀ ( z ) .
Но P ₀( z ) – это постоянная. Приравнивая коэффициенты при z n , находим что она равна a_n . В результате получаем формулу разложения многочлена на множители:
(1) P_n ( z ) = a_n ( z – z ₁ )( z – z ₂ ) . ( z – z _n ) .

Числа z_i являются корнями многочлена P_n ( z ) .

В общем случае не все z_i , входящие в (1), различны. Среди них могут оказаться одинаковые значения. Тогда разложение многочлена на множители (1) можно записать в виде:
(2) P_n ( z ) = a_n ( z – z ₁ ) n ₁ ( z – z ₂ ) n ₂ . ( z – z _k ) n_k ;
.
Здесь z_i ≠ z_j при i ≠ j . Если n_i = 1 , то корень z_i называется простым. Он входит в разложение на множители в виде ( z–z_i ) . Если n_i > 1 , то корень z_i называется кратным корнем кратности n_i . Он входит в разложение на множители в виде произведения n_i простых множителей: ( z–z_i )( z–z_i ) . ( z–z_i ) = ( z–z_i ) n_i .

Многочлены с действительными коэффициентами

Далее мы считаем, что многочлен

имеет действительные коэффициенты a_i .

Лемма 2

Если – комплексный корень многочлена с действительными коэффициентами, , то комплексно сопряженное число также является корнем многочлена, .

Доказательство

Действительно, если , и коэффициенты многочлена – действительные числа, то .

Таким образом, комплексные корни входят в разложение на множителями парами со своими комплексно сопряженными значениями:
,
где , – действительные числа.
Тогда разложение (2) многочлена с действительными коэффициентами на множители можно представить в виде, в котором присутствуют только действительные постоянные:
(3) ;
.

Методы разложения многочлена на множители

С учетом сказанного выше, для разложения многочлена на множители, нужно найти все корни уравнения P_n(z) = 0 и определить их кратность. Множители с комплексными корнями нужно сгруппировать с комплексно сопряженными. Тогда разложение определяется по формуле (3).

Таким образом, метод разложения многочлена на множители заключается в следующем:
1. Находим корень z ₁ уравнения P_n ( z ₁) = 0 .
2.1. Если корень z ₁ действительный, то в разложение добавляем множитель ( z – z ₁) и делим многочлен P_n(z) на ( z – z ₁) . В результате получаем многочлен степени n – 1 :
.
Далее повторяем процесс для многочлена P_{n– 1} (z) , начиная с пункта 1, пока не найдем все корни.
2.2. Если корень комплексный, то и комплексно сопряженное число является корнем многочлена. Тогда в разложение входит множитель

,
где b ₁ = – 2 x ₁ , c ₁ = x ₁ 2 + y ₁ 2 .
В этом случае, в разложение добавляем множитель ( z 2 + b ₁ z + c ₁) и делим многочлен P_n(z) на ( z 2 + b ₁ z + c ₁) . В результате получаем многочлен степени n – 2 :
.
Далее повторяем процесс для многочлена P_{n– 2} (z) , начиная с пункта 1, пока не найдем все корни.

Нахождение корней многочлена

Главной задачей, при разложении многочлена на множители, является нахождение его корней. К сожалению, не всегда это можно сделать аналитически. Здесь мы разберем несколько случаев, когда можно найти корни многочлена аналитически.

Корни многочлена первой степени

Многочлен первой степени – это линейная функция. Она имеет один корень. Разложение имеет только один множитель, содержащий переменную z :
.

Корни многочлена второй степени

Чтобы найти корни многочлена второй степени, нужно решить квадратное уравнение:
P ₂( z ) = a ₂ z 2 + a ₁ z + a ₀ = 0 .
Если дискриминант 0″ style=»width:167px;height:22px;vertical-align:-12px;background-position:-392px -473px»> , то уравнение имеет два действительных корня:
, .
Тогда разложение на множители имеет вид:
.
Если дискриминант D = 0 , то уравнение имеет один двукратный корень:
;
.
Если дискриминант D 0 , то корни уравнения комплексные,
.

Многочлены степени выше второй

Существуют формулы для нахождения корней многочленов 3-ей и 4-ой степеней. Однако ими редко пользуются, поскольку они громоздкие. Формул для нахождения корней многочленов степени выше 4-ой нет. Несмотря на это, в некоторых случаях, удается разложить многочлен на множители.

Нахождение целых корней

Если известно, что многочлен, у которого коэффициенты – целые числа, имеет целый корень, то его можно найти, перебрав все возможные значения.

Лемма 3

Пусть многочлен
,
коэффициенты a_i которого – целые числа, имеет целый корень z ₁ . Тогда этот корень является делителем числа a ₀ .

Доказательство

Перепишем уравнение P_n ( z ₁) = 0 в виде:
.
Тогда – целое,
M z ₁ = – a ₀ .
Разделим на z ₁ :
.
Поскольку M – целое, то и – целое. Что и требовалось доказать.

Поэтому, если коэффициенты многочлена – целые числа, то можно попытаться найти целые корни. Для этого нужно найти все делители свободного члена a ₀ и, подстановкой в уравнение P_n ( z ) = 0 , проверить, являются ли они корнями этого уравнения.
Примечание. Если коэффициенты многочлена – рациональные числа, , то умножая уравнение P_n ( z ) = 0 на общий знаменатель чисел a_i , получим уравнение для многочлена с целыми коэффициентами.

Нахождение рациональных корней

Если коэффициенты многочлена – целые числа и целых корней нет, то при a_n ≠ 1 , можно попытаться найти рациональные корни. Для этого нужно сделать подстановку
z = y/a_n
и умножить уравнение на a_n n- 1 . В результате мы получим уравнение для многочлена от переменной y с целыми коэффициентами.Далее ищем целые корни этого многочлена среди делителей свободного члена. Если мы нашли такой корень y_i , то перейдя к переменной x , получаем рациональный корень
z_i = y_i /a_n .

Полезные формулы

Приведем формулы, с помощью которых можно разложить многочлен на множители.

В более общем случае, чтобы разложить многочлен
P_n ( z ) = z n – a ₀ ,
где a ₀ – комплексное, нужно найти все его корни, то есть решить уравнение:
z n = a ₀ .
Это уравнение легко решается, если выразить a ₀ через модуль r и аргумент φ :
.
Поскольку a ₀ не изменится, если к аргументу прибавить 2 π , то представим a ₀ в виде:
,
где k – целое. Тогда
;
.
Присваивая k значения k = 0, 1, 2, . n– 1 , получаем n корней многочлена. Тогда его разложение на множители имеет вид:
.

Биквадратный многочлен

Рассмотрим биквадратный многочлен:
.
Биквадратный многочлен можно разложить на множители, без нахождения корней.

Далее раскладываем квадратные многочлены на множители, если соответствующие многочлены имеют действительные корни.

Бикубический и многочлены, приводящиеся к квадратному

Рассмотрим многочлен:
.
Его корни определяются из уравнения:
.
Оно приводится к квадратному уравнению подстановкой t = z n :
a _{2 n} t 2 + a_n t + a ₀ = 0 .
Решив это уравнение, найдем его корни, t ₁ , t ₂ . После чего находим разложение в виде:
.
Далее методом, указанным выше, раскладываем на множители z n – t ₁ и z n – t ₂ . В заключении группируем множители, содержащие комплексно сопряженные корни.

Возвратные многочлены

Многочлен называется возвратным, если его коэффициенты симметричны:

Пример возвратного многочлена:
.

Если степень возвратного многочлена n – нечетна, то такой многочлен имеет корень z = –1 . Разделив такой многочлен на z + 1 , получим возвратный многочлен степени n – 1 .
Если степень возвратного многочлена n – четна, то подстановкой , он приводится к многочлену степени n/ 2 . См. Пример с возвратным многочленом >>>.

Автор: Олег Одинцов . Опубликовано: 11-06-2015 Изменено: 30-04-2016