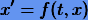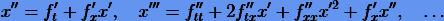Метод разложения в ряд дифференциального уравнения

Разложение решения уравнения в степенной ряд

Этот прием является особенно удобным в применении к линейным дифференциальным уравнениям. Проиллюстрируем его применение на примере уравнения второго порядка. Пусть дано дифференциальное уравнение второго порядка

Предположим, что коэффициенты и представляются в виде рядов, расположенных по целым положительным степеням , так что уравнение (1) можно переписать в виде

Решение этого уравнения будем искать также в виде степенного ряда

Подставляя это выражение и его производных в (2), получаем

Перемножая степенные ряды, собирая подобные члены и приравнивая нулю коэффициенты при всех степенях в левой части (4), получаем ряд уравнений:

Каждое последующее из уравнений (5) содержит одним искомым коэффициентом больше, чем предыдущее. Коэффициенты и остаются произвольными и играют роль произвольных постоянных. Первое из уравнений (5) дает , второе дает , третье — , и т.д. Вообще из (к + 1)-го уравнения можно определить , зная .

Практически удобно поступать следующим образом. Определим по описанной выше схеме два решения и , причем для выберем и , а для выберем и , что равносильно следующим начальными условиям:

Всякое решение уравнения (1) будет линейной комбинацией решений и .

Если начальные условия имеют вид , то очевидно,

Имеет место следующая теорема.

Теорема. Если ряды и сходятся при , то построенный указанным выше способом степенной ряд (3) будет также сходящимся при этих значениях и явится решением уравнения (1).

В частности, если и — многочлены от , то ряд (3) будет сходиться при любом значении .

Пример 1. Найти решения уравнения в виде степенного ряда.

Решение. Ищем в виде ряда , тогда

Подставляя и в (6), получаем

Приводя в (7) подобные члены и приравнивая нулю коэффициенты при всех степенях , получаем соотношения, из которых найдем коэффициенты

Положим для определенности, что . Тогда легко находим, что

Метод разложения в ряд дифференциального уравнения

2. Метод разложения в ряд Тейлора

Одним из старейших методов решения дифференциальных уравнений является метод разложения в ряд Тейлора.

Обратимся к скалярному случаю. Пусть требуется найти решение уравнения (1.1)

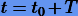
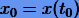
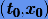
для заданного значения при начальном условии . Потребуем, чтобы ƒ была аналитична в точке . Дифференцируя уравнение по t, будем иметь

Подставляя , последовательно получаем

Таким образом, при достаточно малом T приближенное решение в окрестности t₀ можно представить в виде ряда Тейлора

Оборвем (усечем) ряд (2.2) на p-м члене. Тогда получим приближенную формулу р-порядка

Нетрудно видеть, что при малых T погрешность Δx (ошибка усечения) будет определяться главным образом первым членом ряда (2.4):

Его называют главным членом погрешности.

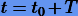
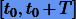
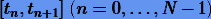
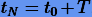
Если для ряд Тейлора (2.2) расходится или ошибка приближенной формулы (2.3) довольно большая, то прибегают к так называемому пошаговому интегрированию. Разбивают на малые отрезки , где 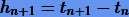, и последовательно получают приближенные решения по формуле

где — n-й шаг интегрирования.

Рассмотрим частные случаи. Для p = 1 и p = 2 с постоянным шагом h имеем формулы

Главным недостатком метода разложения в ряд Тейлора является то, что для получения производных (2.1) необходимо знать производные от ƒ как функции t и x. Очевидно, если ƒ — сложная функция, получение этих производных может представлять собой весьма утомительное занятие. В связи с этим методы разложения в ряд Тейлора редко используются на практике.

Впрочем, в небесной механике имеет место ряд важных с прикладной точки зрения задач, где, используя специфику дифференциальных уравнений, удается получить достаточно простые рекуррентные соотношения для временных производных в разложениях Тейлора. В 1957 г. К. Стеффенсен путем введения новых вспомогательных переменных вывел подобные соотношения для численного интегрирования уравнений планетной задачи.

Рассмотрим идею метода Стеффенсена на примере нормализованных уравнений задачи двух тел:

Если ввести вспомогательные переменные 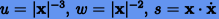и , то уравнение (2.9) можно привести к дифференциально-алгебраической системе уравнений с квадратичными правыми частями

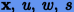
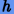
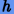
Тогда, подставляя в (2.10) степенные ряды для и по малому параметру и приравнивая коэффициенты при одинаковых степенях , получим для них рекуррентные формулы:

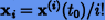
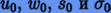
При этом Коэффициенты нулевого порядка вычисляются по начальным данным .

Подобный подход также применяется и для численного интегрирования более сложных дифференциальных уравнений небесной механики, в частности, задачи нескольких тел в классической постановке.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Основные понятия

Определение.Уравнение вида

связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка.

Определение. Общим решением дифференциального уравнения n-го порядка называется функция у = φ(х, С1,С2,…,Сn), которая зависит от аргумента х и n независимых произвольных постоянных С1, С2, …, Сn, обращающая вместе со своими производными у’, у»,…, у(n) уравнение (*) в тождество.

Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С1, С2, …, Сn определенные числовые значения.

Линейные дифференциальные уравнения первого порядка

Определение. Уравнение вида y’+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение вида y»+ρy’+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.

Рассмотрим линейное уравнение второго порядка вида:

у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.

называется характеристическим уравнением данного уравнения (1).

Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К1 и К2.

Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ2–4q уравнения (2) следующим образом:

1. При D>0 корни характеристического уравнения вещественные и различные (К1≠К2), и общее решение имеет вид .

2. При D=0 корни характеристического уравнения вещественные и равные (К1=К2=К), и общее решение имеет вид:

От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.

Дифференциальные уравнения с разделяющимися переменными

5) Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Если оба ряда сходятся, то их сумма сходится, если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из рядов сходится абсолютно, то произведение рядов сходится.

Определение числового ряда.

Сходимость ряда.

Бесконечным числовым рядом называется выражение u1+u2+. +un+. , (1)

содержащее неограниченное число членов, где

u1 , u2 , u3 , . , un , .

— бесконечная числовая последовательность; un называется общим членом ряда.

Определение: Ряд называется сходящимся, если сумма первых его n членов стремится к конечному пределу S, называемому суммой ряда.

Геометри́ческая прогре́ссия — последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии), где , : [1].

В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда.

9,10) Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Особенно часто и эффективно степенные ряды используются для точного и приближенного решения дифференциальных уравнений, обыкновенных и с частными производными. Не вдаваясь в сложные теоретические обоснования, рассмотрим дифференциальное уравнение Бесселя

x2y» + xy’ + (x2 — n2)y = 0,

где n — постоянная (необязательно целая), x — независимая переменная, а y = y(x) — искомая функция. Решения этого уравнения, называемые функциями Бесселя, нашли применение практически во всех областях современного естествознания.

Будем искать y в виде обобщенного степенного ряда

где p, ak — неизвестные постоянные, причем a0 ? 0. Дифференцируя этот ряд дважды под знаком суммы, подставим выражения функции y и ее производных y’, y» в уравнение (7). Затем сделаем приведение подобных членов, и коэффициенты полученного ряда приравняем нулю. После этого получим бесконечную систему уравнений

ak[(p + k)2 — n2] + ak — 2 = 0, k = 2, 3, 4, _,

p = ? n, a1 = a3 = a5 = _ = 0,

В случае нецелого n функции y1(x) и y2(x), соответствующие значениям p = n и p = — n, являются линейно-независимыми и любое другое решение дифференциального уравнения (7) имеет вид y = c1y1(x) + + c2y2(x), где c1 , c2 — постоянные. В случае целого n эти функции отличаются друг от друга только постоянным множителем, поэтому определяют лишь одно из двух линейно-независимых решений дифференциального уравнения.

14)

Дискретной случайной величинойназывается такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.