Метод рунге кутта для решения дифференциальных уравнений excel

Pers.narod.ru. Обучение. Excel: Решение обыкновенных дифференциальных уравнений (задача Коши)

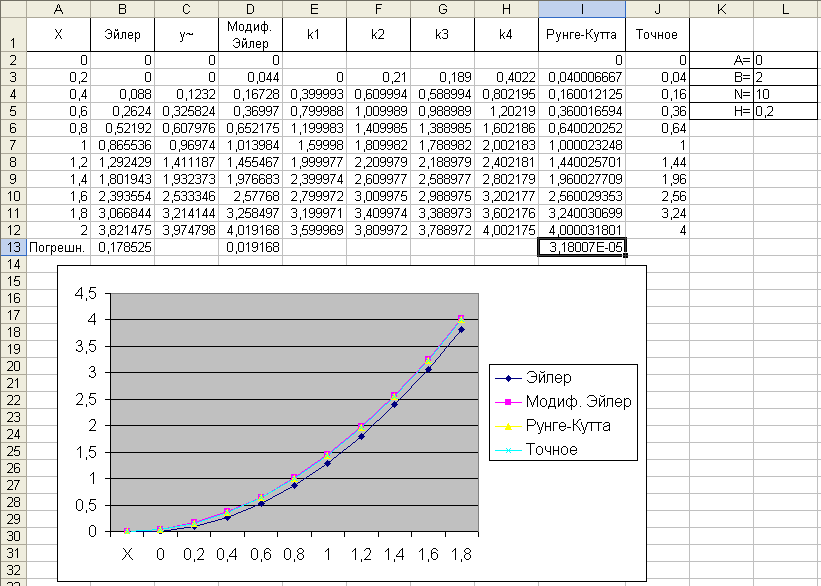
Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.

В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x₀,x_n] при условии y(x₀)=y₀ и равномерном шаге сетки по x .

Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.

Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2] , начальное значение y(0)=0 , для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в норме L₁ , как и принято в данном случае.

Скачать пример в Excel XP/2003 (28 Кб)

Рунге-Кутта VBA EXCEL

Решение дифференциальных уравнений первого порядка
методом Рунге-Кутта.

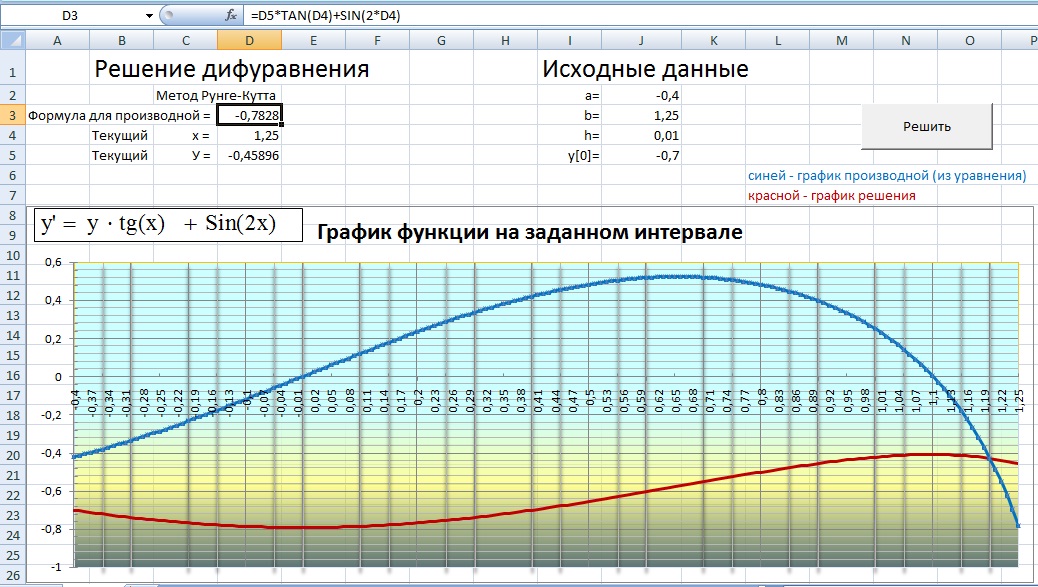
Данный проект VBA позволяет решать дифференциальные уравнения первого порядка одним из численных методов, а именно, методом Рунге-Кутта.

Исходные данные:

границы интервала a и b;
шаг интегрирования h;
начальное значение для решения y(a), позволяющее правильно определить константу…

вводятся в соответствующие ячейки столбца «J».

И самое главное (самая ответственная часть) необходимо без ошибок ввести формулу в ячейку «D3». Эта формула получается из заданного уравнения и представляет функцию, являющуюся производной от решения. Ее параметрами может быть как только х (т.е. ячейка «D4»), так и х совместно с у (т.е. ячейкой «D5»). На рисунке показан пример ввода формулы для заданного уравнения…
В ячейки «D4» и «D5» вводить ничего не нужно… Туда значения будет подставлять макрос…

Если не удалось запустить видео, воспользуйтесь этой ссылкой . видео на YouTube

После этого остается нажать кнопку «Решить» и … если Вы не забыли включить макросы, то увидите, быстро меняющиеся текущие значения в ячейках столбца «D», а после окончания цикла расчета значений у, произойдет изменение графиков.

Графики должны быть построены на заданном Вами интервале (на рисунке от -0,4 до 1,25)…
В каждой точке, где производная (график синего цвета) пересекает ось 0У, функция решения(красная) должна иметь экстремум (максимум или минимум)…
Если терпением Вы не отличаетесь, то не задавайте очень длинный интервал и/или очень мелкий шаг…

Подсказка:
Собственно, процедура заполнения массивов х и у по методу Рунге-Кутта будет выглядеть так:
(при этом глобальная переменная D3formula предварительно инициализируется: D3formula = Range(«D3»).Formula)

Private Function func(x As Double, y As Double) As Double ‘производная
Dim f As String
‘функция вычисляется по формуле, введенной пользователем в ячейку D3 (гед D4 — это x, D5 — это y)
f = Replace(D3formula, «D4», CStr(x))
f = Replace(f, «D5», CStr(y))
Range(«D3»).FormulaLocal = f
func = Range(«D3»)
End Function

Sub MethodRungeKutta()
‘вспомогательные переменные
Dim k1 As Double, k2 As Double, k3 As Double, k4 As Double
Dim i As Integer

For i = 1 To n ‘нулевые значения уже есть

x(i) = x(0) + i * h
k1 = func(x(i — 1), y(i — 1))
k2 = func(x(i — 1) + h / 2, y(i — 1) + k1 * h / 2)
k3 = func(x(i — 1) + h / 2, y(i — 1) + k2 * h / 2)
k4 = func(x(i), y(i — 1) + k3 * h)

y(i) = y(i — 1) + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4) ‘значения вычисляются
p(i — 1) = k1 ‘сохранение в массив для графика

Чтобы на диаграмме отобразились рассчитанные графики, производится заполнение соответствующих диапазонов в столбцах «AA-AB-AC»… Можете сравнить результаты с этим табличным вариантом.

ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Сдвижков О.А.

Приведены программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка точности. Параметрами функций являются начальное и конечное значения независимой переменной, массив начальных значений зависимых переменных и число шагов, в программных кодах применяются динамические массивы. Пользовательские функции можно применять к задаче Коши и одного дифференциальных уравнений 1-го порядка. Все пользовательские функции имеют описания, поясняющие их назначения. Применение пользовательских функций показано на конкретных примерах численного решения задачи Коши системы дифференциальных уравнений 1-го порядка и отдельных дифференциальных уравнений 1-го порядка.

EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A CAUCHY PROBLEM OF THE FIRST-ORDER ODE SYSTEM

The current study presents program codes of custom VBA Excel functions that implement numerical methods for solving the Cauchy problem for a system of 1st order ordinary differential equations using the Euler and Runge-Kutta 4th order methods. The parameters of the functions are the initial and final values of the independent variable, an array of initial values of the dependent variables, and the number of steps. Program codes use dynamic arrays. Custom functions can be applied to the Cauchy problem and one of the 1st order differential equations. All of the custom functions have descriptions that explain their purpose. The article demonstrates the use of custom functions using specific examples of numerical solutions to the Cauchy problem of 1st order differential equations system and individual 1st-order differential equations.

Текст научной работы на тему «ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА»

ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ СИСТЕМЫ ОДУ 1-ГО ПОРЯДКА

Российский государственный университет туризма и сервиса, Пушкино МО, Россия * Корреспондирующий автор (oasdv[at]yandex.ru)

Приведены программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка точности. Параметрами функций являются начальное и конечное значения независимой переменной, массив начальных значений зависимых переменных и число шагов, в программных кодах применяются динамические массивы. Пользовательские функции можно применять к задаче Коши и одного дифференциальных уравнений 1-го порядка. Все пользовательские функции имеют описания, поясняющие их назначения. Применение пользовательских функций показано на конкретных примерах численного решения задачи Коши системы дифференциальных уравнений 1 -го порядка и отдельных дифференциальных уравнений 1 -го порядка.

Ключевые слова: система дифференциальных уравнений, задача Коши, численные методы, код, диалоговое окно.

EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A CAUCHY PROBLEM OF THE FIRST-ORDER ODE SYSTEM

Russian State University of Tourism and Service, Pushkino, Moscow Oblast, Russia * Corresponding author (oasdv[at]yandex.ru)

Keywords: system of differential equations, Cauchy problem, numerical methods, code, dialog box.

Системы обыкновенных дифференциальных уравнений 1-го порядка имеют большое прикладное значение [9]. Однако численные методы решения задачи Коши системы обыкновенных дифференциальных уравнений 1 -го порядка отличаются большой трудоемкостью [1], [2], [6]. Поэтому задача информатизации этих методов, доступной самому широкому кругу пользователей ПК, каким является круг пользователей Microsoft Office, несомненно, является актуальной.

Цель данного исследования — разработка на языке программирования VBA Excel [3], [4], [7] программных кодов пользовательских функций [10], которыми численно решается задача Коши системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта.

Программный код функции VBA Excel для решения методом Рунге-Кутта системы двух дифференциальных уравнений приведен в [5]. Пользовательские функции VBA Excel для численного решения задачи Коши обыкновенного дифференциального уравнения 1-го порядка приведены в [9].

1. Пользовательская функция ЭЙЛЕР

В методе Эйлера численного решения задачи Коши системы дифференциальных уравнений

dyL = f1(Х У1, У 2 Ут ) ах

= Л(Х У1, У 2 Ут ) „ 1Ч

йУт = /т (Х У1, У2 Ут )

У1( Хо) = У°, У2(Хо) = У20,-, Ут (Хо) = У0т (1.2)

на отрезке [хо, xo + n h] применяется формула:

у л = У ji-1 + h • f (хо + (i — 1)h Уи-1> У 2 i-iv, Ут1-1) (1.3)

j = 1, 2, . m; i= 1, 2, . n.

Правые части системы (1.1) в VBA Excel можно задать пользовательской функцией СИСТЕМ, листинг которой имеет вид:

Function СИСТЕМ (Массив As Variant)

‘массив состоит из значений^ — номера уравнения,х,у1,у2. yn Select Case Массив(1) Case 1

СИСТЕМ = /1(Массив(2), Массив(3), . Массив(т)) Case 2

СИСТЕМ = /2(Массив(2), Массив(3), . Массив(т))

СИСТЕМ = /п(Массив(2), Массив(3), . Массив(т)) End Select End Function

Пусть система (1.1) задана пользовательской функцией СИСТЕМ. Тогда пользовательская функция ЭЙЛЕР, код VBA Excel которой приведен в листинге 1, выполняет вычисления по формуле (1.3). Листинг 1. Код функции ЭЙЛЕР и ее описания Function ЭйЛЕР(Нач_х0, Конеч_х, Нач_у0(), Шагов) As Variant Dim n As Integer, m As Integer, x(), y(), z(), c() n = Шагов:т = иВоиМ(Нач_у0) ReDim z(1 To m, 0 To n):ReDim x(0 To n) ReDim y(1 To m + 2):ReDim c(1 To m) x(0) = Нач_x0:h = (Конеч_x — x(0)) / n For i = 1 To m z(i, 0) = Нач_у0® Next

Forj = 1 To n For i = 1 To m

y(1) = i: y(2) = x(0) + h * (j — 1) For r = 3 To m + 2 y(r) = z(r — 2, j — 1) Next

z(i, j) = z(i, j — 1) + h * СИСТЕМ(Массив)

For i = 1 To m c(i) = z(i, n) Next

ЭЙЛЕР = c End Function Sub InstallFunc2()

Application.MacroOptions Macш:=»ЭИЛЕР», Descriptions _ «Возвращает значения yi, полученные методом Эйлера» End Sub

В листинг 1 входят массивы:

z(1 To m, 0 To n)- двумерный массив значений функцийу1, у2, . ym в точках x0, x0+h, . x0+n h; x(0 To n) — массив значений х0, x0+h, . x0+nh;

y(1 To m + 2) — массив значений (i, x, y1, y2, . ym), где i — номер уравнения системы;

c(1 To m) — массив итоговых значений массива z.

Пример 1.1. Найти приближенные значения решения системы

с начальными условиями у (0) = 0, у2(0) = 1. Вычислить значения решения при х=0,1; 0,2; 0,3; 0,4.

1. В стандартный модуль вводится листинг функции СИСТЕМ: Function СИСТЕМ(Массив As Variant)

Select Case Массив (1) Case 1

СИСТЕМ = Массив (4) Case 2

СИСТЕМ = Массив (3) End Select End Function

2. В диапазон А1:А5 вводятся значения, принимаемые переменной х: 0; 0,1; 0,2; 0,3; 0,4.

3. В диапазон В1:С1 вводятся начальные значения, принимаемые у1 и у2: 0 и 1.

4. Выделяется диапазон В2:С2, вызывается функция ЭЙЛЕР и вводятся данные:

Рис. 1.1 — Применение функции ЭЙЛЕР в примере 1.1

5. Команда Ог^Ый +Enter возвращает в диапазоне В2:С2 результаты.

6. Копирование данных диапазона В2:С2 в диапазон В3:С5 завершает решение задачи (рис. 1.2).

Рис. 1.2 — Вид решения примера 1.1 функцией ЭЙЛЕР Пример 1.2. Найти приближенные значения решения системы

с начальными условиями у (0) = 1, у2(0) = 2, у3 (0) = 3. Вычислить значения решения при х=0,1; 0,2; 0,3; 0,4; 0,5.

1. В стандартный модуль вводится листинг функции СИСТЕМ: Function СИСТЕМ(Массив As Variant) Select Case Массив(1) Case 1

СИСТЕМ = Массив(4) + Массив(5) Case 2

СИСТЕМ = Массив(3) + Массив(5) Case 3

СИСТЕМ = Массив(3) + Массив(4)

End Select End Function

2. В диапазон А1:А6 вводятся значения, принимаемые х: 0; 0,1; 0,2; 0,3; 0,4; 0,5.

3. В диапазон B1:D1 вводятся начальные значения, принимаемые yi, у2, у3: 1, 2, 3.

4. Выделяется диапазон B2:D2, вызывается функция ЭЙЛЕР и вводятся данные:

Рис. 1.3 — Применение функции ЭЙЛЕР в примере 1.2

5. Команда Ог1+8Ый +Бйег возвращает в диапазоне В2:Б2 результаты.

6. Копирование данных диапазона В2:Б2 в диапазон В3:Б6 завершает решение задачи (рис. 1.4).

J 0,2 2,07 2,88 3,69

4 0,3 2,727 3,456 4,185

5 0,4 3,4911 4,1472 4,8033

Б 0,5 4,38615 4,97664 15,56713

Рис. 1.4 — Вид решения примера 1.2 функцией ЭЙЛЕР

Функция Эйлер применима и к задаче Коши обыкновенного дифференциального уравнения 1 -го порядка. Пример 1.3. Найти приближенные значения решения задачи Коши

на отрезке [0, 1], разбивая отрезок на 10 равных частей. В этом случае код функции СИСТЕМ имеет вид: Function СИСТЕМ(Массив As Variant) СИСТЕМ = Массив(2) + Массив(3) End Function

Применение функции ЭЙЛЕР приводит к результатам, показанным на рисунке 1.3.

В с D Е F G Н 1 J К

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

1,1 1,22 1,362 1,5282 1,72102 1,943122 2,197434 2,487178 2,815895 3,187485]

Рис. 1.5 — Вид решения примера 1.3 функцией ЭЙЛЕР

2. Пользовательская функция РУНГЕ

В методе Рунге-Кутта четвертого порядка точности, которым численно решается задача Коши (1.1, 1.2):

k(2) = fj (x. + h / 2, уи + h ■ С / 2. уш + h • k« /2), (2.2)

k(? = fj (x + h /2, yH + h ■ k^ / 2. у„г + h ■ кП2) / 2), k(4 = fj(x + h,yw + h ■ *£>. уйг + h ■ О.

Пусть система (1.1) задана пользовательской функцией СИСТЕМ. Тогда пользовательская функция РУНГЕ, программный код VBA Excel которой приведен в листинге 2, выполняет вычисления по формулам (2.1), (2.2). Листинг 2. Код функции РУНГЕ и ее описания Function РУНГЕ(Нач_х, Конеч_х, Нач_у() As Variant, Шагов) _ As Variant

Dim n As Integer, m As Integer, h As Single, x(), y(), z(), c()

n = Шагов:т = иВоиМ(Нач_у)

ReDim z(1 To m, 0 To n):ReDim x(0 To n)

ReDim y(l To m + 2):ReDim c(1 To m)

Dim K(1 To 4) As Double

x(0) = Нач_x:h = (Конеч_х — x(0)) / n

For i = 1 To n Forj = 1 To m

y(1) = j: y(2) = x(0) + h * (i — 1) For r = 3 To m + 2 y(r) = z(r — 2, i — 1) Next

Массив = y:K(1) = h * СИСТЕМ(Массив) y(1) = j: y(2) = x(0) + h * (i — 1) + h / 2 For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(1) / 2 Next

K(2) = h * СИСТЕМ(Массив) y(1) = j: y(2) = x(0) + h * (i — 1) + h / 2 For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(2) / 2 Next

K(3) = h * СИСТЕМ(Массив):y(1) = j: y(2) = x(0) + h * i For r = 3 To m + 2 y(r) = z(r — 2, i — 1) + K(3) Next

K(4) = h * СИСТЕМ(Массив)

z(j, i) = z(j, i — 1) + (K(1) + 2 * K(2) + 2 * K(3) + K(4)) / 6

For i = 1 To m c(i) = z(i, n) Next

РУНГЕ = c End Function Sub InstallFunc3()

Application.MacroOptions Macro:=»РУНГЕ», Description:= _ «Возвращает значения yi, полученн^1е методом Рунге-Кутта» End Sub

В листинге 2 массивы аналогичные массивам листинга 1, только:

K(1 To 4) — массив значений, вычисляемых по формулам (2.2).

Решение примера 1.1 с помощью функции РУНГЕ показано на рисунке 2.1.

3 0,2 0,210342 1,011061

4 0,3 0,316676 1,033103

5 0,4 0,425336 1,066488

Рис. 2.1 — Вид решения примера 1.1 функцией РУНГЕ Решение примера 1.2 с помощью функции РУНГЕ показано на рисунке 2.2.

Л I=РУН ГЕ(0; А2; [1; 2; 3 А2/0,1)>

2 0,1 1,5535 2,4423 3,3321

3 0,2 2,192731 2,933636 3,77449

4 0,3 2,940906 3,644213 4,34752

5 0,4 3,325591 4,451042 5,076493

6 0,5 4,330289 5,436502 5,992716

Рис. 2.2 — Вид решения примера 1.2 функцией РУНГЕ Решение примера 1.3 с помощью функции РУНГЕ показано на рисунке 2.3.

Рис. 2.3 — Вид решения примера 1.3 функцией РУНГЕ

Пример 2.1. Построить с помощью функции РУНГЕ графики численности популяций, описываемых системой Вольтерра — Лотка

при начальных условиях Х1(0)=3, х2(0)=1; параметр 1 принимает значения от 0 до 3.

Расчетная таблица строится по аналогии с таблицей примера 1.1, значения независимой переменной в диапазоне А1:А31, в ячейку В2 вводится формула =РУНГЕ(0;А2;<3;1>;А2/0,01). По таблице строятся графики численности популяций (рис. 2.4).

4 3,5 3 2,5 2 1,5 1

0 0,5 1 1,5 2 2,5 3 Рис. 2.4 — Графики численности популяций

1. Программные коды пользовательских функций VBA Excel, реализующих численные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера и Рунге-Кутта четвертого порядка, публикуются впервые.

2. Как показывают примеры, применение рассматриваемых функций не вызывает трудностей, избавляет от больших объемов рутинных вычислений, позволяет получать результаты по такому сложному разделу, как численные методы решения систем дифференциальных уравнений, на современном (цифровом) уровне.

3. Рассматриваемые пользовательские функции будут полезны как в научных исследования, связанных с системами обыкновенных дифференциальных уравнений 1 -го порядка, так и в учебном процессе.

Конфликт интересов Conflict of Interest

Не указан. None declared.

Список литературы / References

1. Бахвалов Н.С. Численные методы. / Н. С. Бахвалов — М: Наука, 1975. — 632 с.

2. Березин И.С. Методы вычислений, т. II. / И. С. Березин, Н. П. Жидков — М.: ГИФМЛ, 1959. — 620 с.

3. Гарнаев А.Ю. MS Excel 2002: разработка приложений. / А. Ю. Гарнаев — СПб.: БХВ-Петербург, 2003. — 768 с.

4. Кузьменко В.Г. VBA 2003. / В. Г. Кузьменко — М: ООО «Бином-Пресс», 2004, 432 с.

5. Ларсен Р.У. Инженерные расчеты в Excel: Пер. с англ. / Р. У. Ларсен — М.: Издательский дом «Вильямс», 2002. -544 с.

6. Самарский А.А. Задачи и упражнения по численным методам: Учебное пособие. / А. А. Самарский, П. Н. Вабищевич, Е. А. Самарская — М.: Эдиториал УРСС, 2000. — 208 с.

7. Сдвижков О.А. Excel — VBA. Словарь-справочник пользователя / О. А. Сдвижков. — М.: Эксмо, 2008. — 224 с.

8. Сдвижков О.А. Пользовательские функции VBA Excel для численного решения задачи Коши ОДУ 1-го порядка / Сдвижков О.А. // Международный научно-исследовательский журнал, № 4 (106), 2021, Часть 1, стр. 35 — 40.

9. Эрроусмит Д. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями: Пер. с англ. / Д. Эрроусмит, К. Плейс. — М.: Мир, 1986. — 243 с.

10. Сдвижков О.А. DEcode (пользовательские функции) [Электронный ресурс]. — URL: https://oas.ucoz.com/load/odu_polzovatelskie_funkcii/1-1-0-35 (дата обращения: 20.01.2021)

Список литературы на английском языке / References in English

1. Bakhvalov N. S. Chislennye metody [Numerical Methods] / N. S. Bakhvalov-M: Nauka, 1975 — 632 p. [in Russian]

2. Berezin I. S. Metody vychislenijj, t. II. [Methods of Calculations, vol. 2] / I. S. Berezin, N. P. Zhidkov-M.: GIFML, 1959 — 620 p. [in Russian]

3. Garnaev A. Yu. MS Excel 2002: razrabotka prilozhenijj [MS Excel 2002: Application Development] / A. Yu. Garnaev -St. Petersburg: BKhV-Petersburg, 2003 — 768 p. [in Russian]

4. Kuzmenko V. G. VBA 2003 / V. G. Kuzmenko-M: «Binom-Press» LLC, 2004, 432 p. [in Russian]

5. Larsen R. U. Inzhenernye raschety v Excel: Per. s angl. [Engineering Calculations in Excel: Translation from English] / R. U. Larsen-M.: Publishing house «Vilyams», 2002 — 544 p. [in Russian]

6. Samarsky A. A. Zadachi i uprazhnenija po chislennym metodam: Uchebnoe posobie [Problems and Exercises in Numerical Methods: A Textbook] / A. Samara, P. N. Vabishchevich, E. A. Samarskaya -M.: Ehditorial URSS, 2000 — 208 p. [in Russian]

7. Sdvizhkov O. A. Excel — VBA. Slovar’-spravochnik pol’zovatelja [Excel — VBA. Dictionary-User reference] / O. A. Sdvizhkov. — M.: Eksmo, 2008 — 224 p. [in Russian]

8. Sdvizhkov O. A. Pol’zovatel’skie funkcii VBA Excel dlja chislennogo reshenija zadachi Koshi ODU 1-go porjadka [Custom Excel VBA Functions For Numerical Solution of a First-Order Cauchy Ode] / O. A. Sdvizhkov // Mezhdunarodnyjj nauchno-issledovatel’skijj zhurnal [International Research Journal], No. 4 (106), 2021, Part 1, pp. 35-40 [in Russian]

9. Arrowsmith D. Obyknovennye differencial’nye uravnenija. Kachestvennaja teorija s prilozhenijami [Ordinary Differential Equations: A Qualitative Approach with Applications]: Translation from English / D. Arrowsmith, C. M. Place. — Moscow: Mir, 1986 — 243 p. [in Russian]

источники:

http://orenstudent.ru/RungeKuttaVBA_change_formula.htm

http://cyberleninka.ru/article/n/funktsii-vba-excel-dlya-chislennogo-resheniya-zadachi-koshi-sistemy-odu-1-go-poryadka

Метод рунге кутта для решения дифференциальных уравнений excel