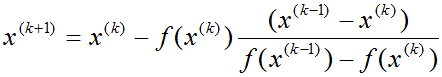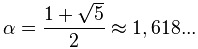Метод секущих решение уравнений на с

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Метод хорд

Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.

Метод хорд (то же, что метод секущих) — итерационный метод решения нелинейного уравнения.

Нелинейное уравнение — это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.

Метод хорд. Алгоритм

Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.

Итерационная формула для вычислений методом хорд следующая:

Вычисления продолжаются до тех пор, пока не станет истинным выражение:

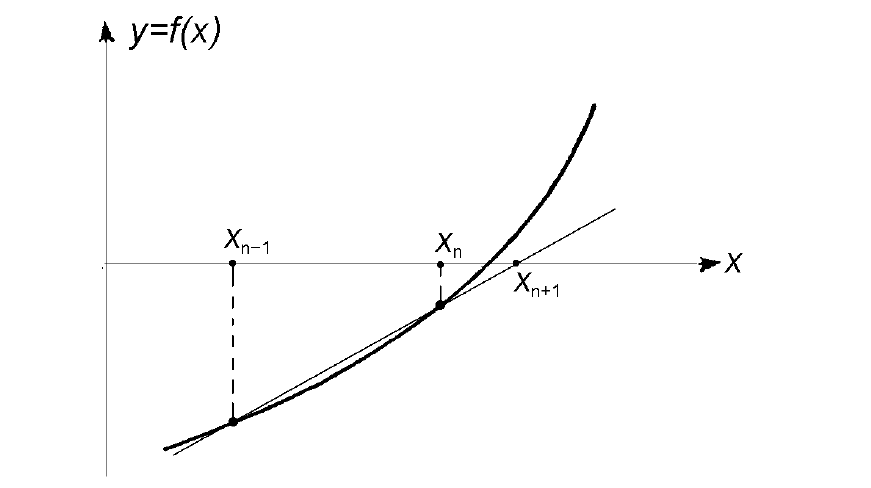
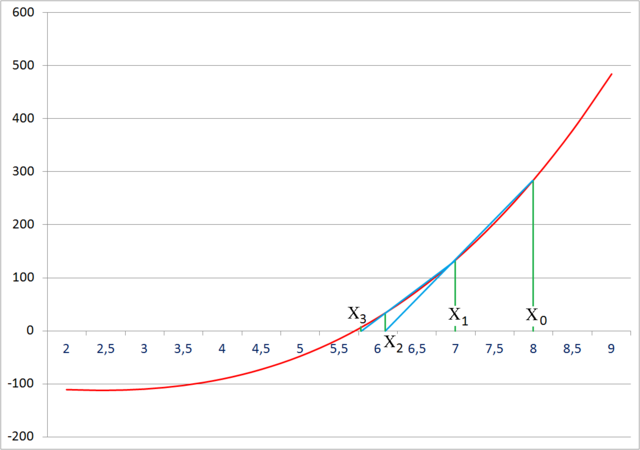
Геометрическая модель одного шага итераций метода хорд представлена на рисунке:

Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:

Метод хорд. Программная реализация

Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.

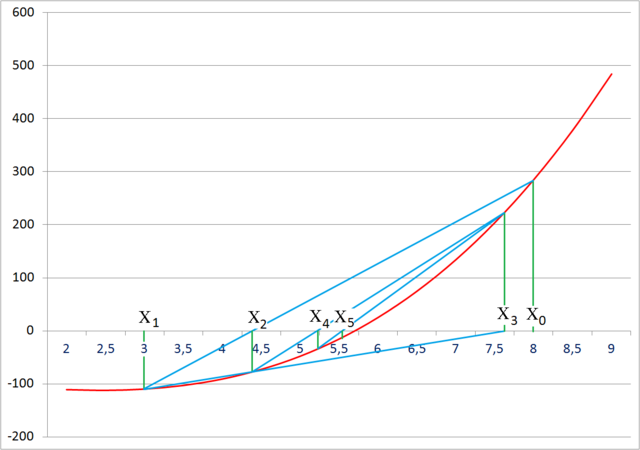
В качестве примера ищется корень уравнения x 3 — 18x — 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).

x_prev — это x_k-1, x_curr — это x_k, x_next — это x_k+1.

Метод секущих

Метод секущих — итерационный численный метод приближённого нахождения корня уравнения.

Немного теории о методе секущих под калькулятором.

Метод секущих

Метод секущих

Метод секущих — модификация метода Ньютона, в котором производная (вычислять ее не всегда удобно) заменена на секущую.
Секущая — прямая, проходящая через две точки на графике функции. В данном методе процесс итераций состоит в том, что в качестве приближений корню уравнения принимаются последовательные значения точек пересечения секущей с осью абсцисс.

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

Это и есть наша итерационная формула. Графическое отображение метода — на рисунке ниже.

Метод работает и в случае, если начальные точки выбраны по одну и ту же сторону от корня (то есть, корня нет на отрезке между начальными приближениями), но при этом возможны случаи, когда метод не сходится.

Метод секущих является двухшаговым, то есть, новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε.

Приложение 3. Скриншоты работы программы

КУРСОВАЯ РАБОТА

Численные методы интегрирования

Всего листов 18

Выполнил студ. гр. 14-ПМ,

ОСНОВНАЯ ЧАСТЬ. 5

1. Описание методов Ньютона и секущих. 5

2. Практическая реализация алгоритмов. 6

3. Сравнение эффективности алгоритмов. 8

СПИСОК ИСТОЧНИКОВ.. 12

С помощью уравнений описываются многие законы, процессы и явления во многих областях науки. Некоторые уравнения легко решаются аналитически, для других нахождение корня может быть затруднено. Однако существуют алгоритмы, позволяющие вычислить корень равнения с достаточной точностью.

В данной курсовой работе на языке С++ описаны следующие методы численного решения уравнений: метод Ньютона и метод секущих. C++ — компилируемый, статически типизированный язык программирования общего назначения. C++ широко используется для разработки программного обеспечения, являясь одним из самых популярных языков программирования.

Программа выполнена в среде Microsoft Visual Studio 2008. Microsoft Visual Studio — линейка продуктов компании Microsoft, включающих интегрированную среду разработки программного обеспечения и ряд других инструментальных средств.

Для проверки правильности результатов интегрирования и визуализации сходимости полученных решений используется Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением.

В первом пункте основной части рассматриваются общие сведения о методах Ньютона и секущих.

Второй пункт основной части представляет собой описание программной реализации алгоритмов нахождения корня уравнения в рамках индивидуального задания курсовой работы. Описываемый программный код разработан самостоятельно.

Третий пункт основной части представляет собой сравнение эффективности методов Ньютона и секущих. Полученные решения сравниваются с решением в Mathcad.

1. Описание методов Ньютона и секущих

Пусть задана функция действительного переменного. Требуется найти корни уравнения .

Метод Ньютона (метод касательных) описывается следующим образом. Пусть и непрерывны и сохраняют определённые знаки при . Найдя какое-нибудь n-ое приближённое значение корня , можем уточнить метод Ньютона следующим образом.

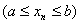
где является малой величиной. Отсюда, применяя формулу Тейлора, получим

Итерации следует продолжать до тех пор, пока не будет достигнута заданная точность, то есть пока не выполнится .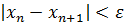

Метод секущих получается из метода касательных заменой разностным приближением:

В результате получим формулу итерационного процесса:

Метод секущих является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями и В методе необходимо задавать два начальных приближения и

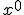
2. Практическая реализация алгоритмов

Рассмотрим реализацию описанных выше алгоритмов на языке С++.

Написано две программы. Первая реализует метод Ньютона, а вторая метод секущих.

Реализация метода Ньютона , представлена в Листинге1.