Метод скорейшего спуска для нелинейных уравнений

Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений

Автор работы: Пользователь скрыл имя, 30 Ноября 2013 в 13:35, курсовая работа

Краткое описание

В настоящее время не существует методов, которые в одинаковой мере были бы хороши для всех систем ЛАУ. Почти все методы являются ориентированными и учитывают тем или иным образом специальные свойства матриц систем ЛАУ.
В курсовом проекте я рассматриваю метод скорейшего спуска. Этот метод не входит в число методов, которые широко используются и часто встречаются в литературе. Он реже используется в практике вычислений, но тем не менее содержит глубокие идеи и входит в основы теории вычислительной алгебры.

Содержание

Введение………………………………………………………. 2
1. Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений……………………….……….3
2. Метод скорейшего спуска для случая системы линейных уравнений…………………………………………………………..11
3. Свойства приближений метода скорейшего спуска……17
Заключение……….………….…………………………………25
Список использованной литературы…………

Прикрепленные файлы: 1 файл

курсач.doc

1. Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений……………………….……….3

2. Метод скорейшего спуска для случая системы линейных уравнений……………………………… …………………………..11

3. Свойства приближений метода скорейшего спуска……17

Список использованной литературы…………….………….26

Задачи численного решения систем линейных алгебраических уравнений (ЛАУ) и систем нелинейных численных уравнений многочисленны и весьма разнообразны. Это в первую очередь объясняется многообразием матриц систем ЛАУ и просто матриц для которых необходимо проводить вычисления.

В настоящее время не существует методов, которые в одинаковой мере были бы хороши для всех систем ЛАУ. Почти все методы являются ориентированными и учитывают тем или иным образом специальные свойства матриц систем ЛАУ.

В курсовом проекте я рассматриваю метод скорейшего спуска. Этот метод не входит в число методов, которые широко используются и часто встречаются в литературе. Он реже используется в практике вычислений, но тем не менее содержит глубокие идеи и входит в основы теории вычислительной алгебры.

Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений.

Пусть имеется система нелинейных уравнений:

Систему (1) удобнее записать в матричном виде:

где — вектор – функция; — вектор – аргумент.

Предположим, что функции действительны и непрерывно дифференцируемы в их общей области определения. Рассмотрим функцию:

Очевидно, что каждое решение системы (1) обращает в нуль функцию U(x); наоборот, числа x₁, x₂, . x_n, для которых функция U(x) равна нулю, являются корнями системы (1).

Будем предполагать, что система (1) имеет лишь изолированное решение, которое представляет собой точку строгого минимума функции U(x). Таким образом, задача сводится к нахождению минимума функции U(x) в n-мерном пространстве

Пусть x – вектор-корень системы (1) и x (0) – его нулевое приближение. Через точку x (0) проведем поверхность уровня функции U(x). Если точка x (0) достаточна близка к корню х, то при наших предположениях поверхность уровня

будет похожа на эллипсоид.

Из точки х (0) двигаемся по нормали к поверхности U(x)=U(x (0) ) до тех пор, пока эта нормаль не коснется в некоторой точке х (1) какой-то другой поверхности уровня.

5.2. Метод градиента (метод скорейшего спуска)

Пусть имеется система нелинейных уравнений:

(5.13)

Систему (5.13) удобнее записать в матричном виде:

(5.14)

Где — вектор – функция; — вектор – аргумент.

Решение системы (5.14), как и для системы линейных уравнений (см. п. 3.8), будем искать в виде

(5.15)

Здесь и — векторы неизвестных на P и P+1 шагах итераций; вектор невязок на P-ом шаге – F(P) = F(X(P)); W‘P – транспонированная матрица Якоби на P – ом шаге;

;

.

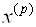
Пример 5.2. Методом градиента вычислим приближенно корни системы

Расположенные в окрестности начала координат.

Выберем начальное приближение:

По вышеприведенным формулам найдем первое приближение:

Аналогичным образом находим следующее приближение:

Ограничимся двумя итерациями (шагами), и оценим невязку:

· Как видно из примера, решение достаточно быстро сходится, невязка быстро убывает.

· При решении системы нелинейных уравнений методом градиента матрицу Якоби необходимо пересчитывать на каждом шаге (итерации).

Вопросы для самопроверки

· Как найти начальное приближение: а) для метода Ньютона; б) для метода градиента?

· В методе скорейшего спуска вычисляется Якобиан (матрица Якоби). Чем отличается Якобиан, вычисленный для СЛАУ, от Якобиана, вычисленного для нелинейной системы уравнений?

· Каков критерий остановки итерационного процесса при решении системы нелинейных уравнений: а) методом Ньютона; б) методом скорейшего спуска?

научная статья по теме МОДИФИЦИРОВАННЫЙ МЕТОД НАИСКОРЕЙШЕГО СПУСКА ДЛЯ НЕЛИНЕЙНЫХ НЕРЕГУЛЯРНЫХ ОПЕРАТОРНЫХ УРАВНЕНИЙ Математика

Цена:

Авторы работы:

Научный журнал:

Год выхода:

Текст научной статьи на тему «МОДИФИЦИРОВАННЫЙ МЕТОД НАИСКОРЕЙШЕГО СПУСКА ДЛЯ НЕЛИНЕЙНЫХ НЕРЕГУЛЯРНЫХ ОПЕРАТОРНЫХ УРАВНЕНИЙ»

ДОКЛАДЫ АКАДЕМИИ НАУК, 2015, том 462, № 3, с. 264-267

МОДИФИЦИРОВАННЫЙ МЕТОД НАИСКОРЕЙШЕГО СПУСКА ДЛЯ НЕЛИНЕЙНЫХ НЕРЕГУЛЯРНЫХ ОПЕРАТОРНЫХ УРАВНЕНИЙ

© 2015 г. Член-корреспондент РАН В. В. Васин

Поступило 12.02.2015 г.

Метод наискорейшего спуска (МНС) для аппроксимации решения нелинейного, в общем случае, нерегулярного уравнения

заданного на паре гильбертовых пространств U, F, имеет вид

при несколько более слабом условии, чем (3),

||А ( и) — /\ |2 0, установлено при у 0. (6)

Институт математики и механики им. Н.Н. Красовского

Уральского отделения Российской Академии наук, Екатеринбург

Уральский федеральный университет им. Б.Н. Ельцина,

Это свойство оператора Т влечет слабую сходимость итераций (4) при выполнении условия слабой замкнутости оператора S.

В статье [4] был предложен регуляризованный метод наискорейшего спуска

k + 1 k ua = ua — Y

(¡AXuka) Sa(ua)|| 2 + a|| Sa(^)||2 (7)

данном сообщении параллельно рассматривается и неравенство (12) принимает вид его регуляризованный аналог для линейного оператора A. В этом случае результаты формулируются в качестве простых следствий из утверждений для нелинейного оператора. Иной подход к итеративной регуляризации а-процессов, в частности МНС, для линейного самосопряженного оператора предложен в [5] (см. теорему 6.3).

Лемма 2. Пусть выполнено 0 справедливо соотношение

+ 1 2 2 + 1 2 иа — ик

Y а и — иа|| -N?N21 ||и-и\\ +

Вместе с (13) это влечет (12).

Из (12), (19) следует сходимость lim ||иа — иа|| = 0,

что завершает доказательство теоремы.

Следствие 3. Для случая линейного оператора неравенство (18) для параметра у принимает

в (22) приводит к неравенству (18) и сходимости итераций. Условие минимума для левой части неравенства (23) дает выражение (20) для параметра Y и наименьшее значение для параметра q, определяемого формулой (21).

Следствие 4. В случае линейного оператора Л с |Л||

> Цыа — u0||. Тогда справедливы соотношения

iim||uOS — u| = 0, ||a(uOg)) -fj = o(5k0,

что означает выполнение регуляризующего свойства алгоритма, построенного на основе двухэтап-ного метода (24), (25).

2. ОЦЕНКА ПОГРЕШНОСТИ МЕТОДА

Чтобы получить оценку погрешности двух-этапного метода (9), (10) и построить одноступенчатый регуляризующий алгоритм потребуются дополнительные предположения (см. [7]):

1) существует константа к > 0 такая, что для всех ы е ^(ы0) найдется элемент у(ы, ы0, е итакой, что выполнены соотношения

[A'( и) — A ( U)] w = A'( «° )у( и, и0, w), и, и0, w)|| ¡A'(u°)||, u° — и = ф(А'(u°)*A'(u°))v, v е U.

Те о р е м а 3 [7]. Пусть ua — решение уравнения (9) и выполнены предположения 1), 2). Тогда справедлива оценка

-и\\ по теме «Математика»

АКИМОВА Е.Н., МАРТЫШКО П.С., МИСИЛОВ В.Е. — 2013 г.