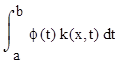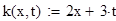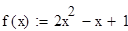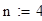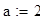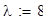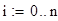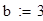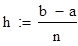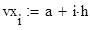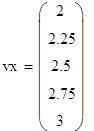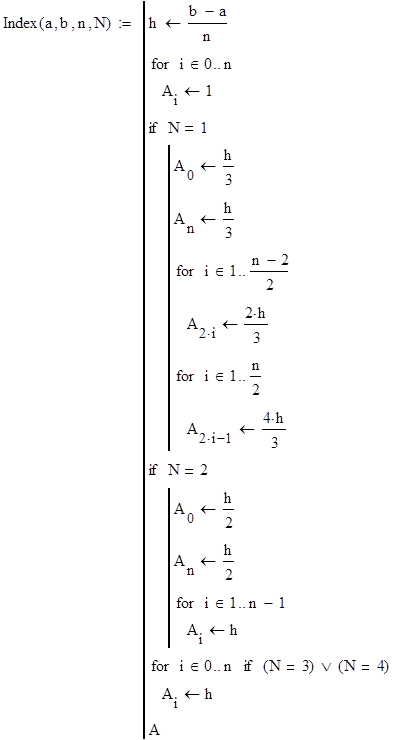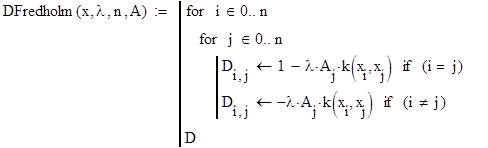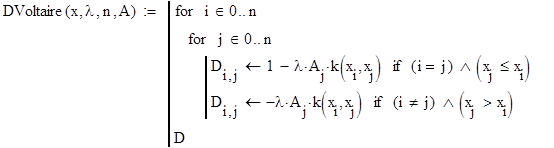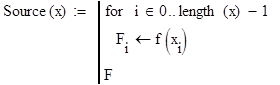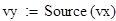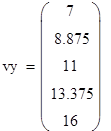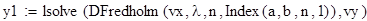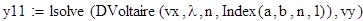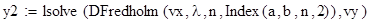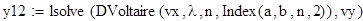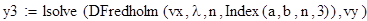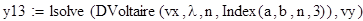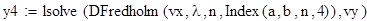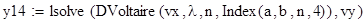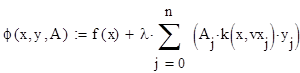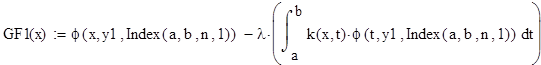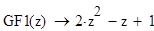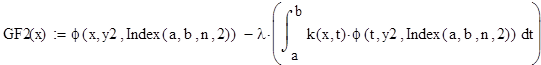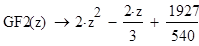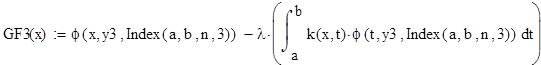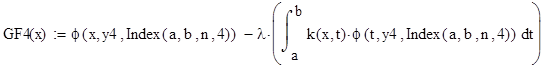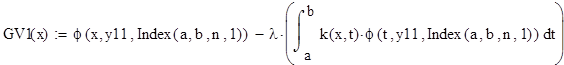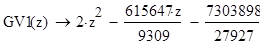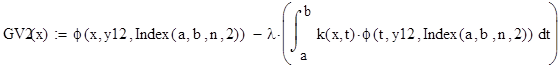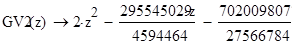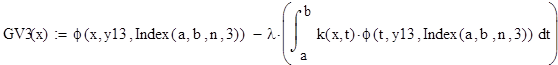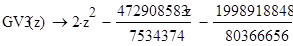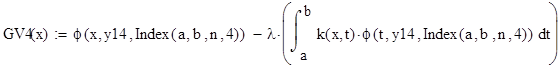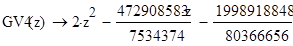Метод сумм решения интегральных уравнений

Метод конечных сумм для линейных интегральных уравнений Вольтерра третьего рода Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Каракеев Таалайбек Тултемирович, Бугубаева Жумгалбубу

В работе рассмотрены вопросы приближенного решения линейных интегральных уравнений Вольтерра третьего рода методом конечных сумм. На основе сингулярно-возмущенного уравнения с использованием квадратурной формулы правых прямоугольников осуществлен переход к системе алгебраических уравнений. Доказана сходимость приближенного решения к точному решению исходного уравнения.

Похожие темы научных работ по математике , автор научной работы — Каракеев Таалайбек Тултемирович, Бугубаева Жумгалбубу

Текст научной работы на тему «Метод конечных сумм для линейных интегральных уравнений Вольтерра третьего рода»

Метод конечных сумм для линейных интегральных уравнений Вольтерра третьего рода Каракеев Т. Т.1, Бугубаева Ж.2

1Каракеев Таалайбек Тултемирович / Кагакееу ТааЫЬек Тыкет1гоу1Л — доктор физико-математических наук, профессор; 2Бугубаева Жумгалбубу /Бы^Ьаеуа ZhumgalЬuЬu — старший преподаватель, кафедра информатики и вычислительной техники, Кыргызский национальный университет им. Ж. Баласагына, г. Бишкек, Кыргызская Республика

Аннотация: в работе рассмотрены вопросы приближенного решения линейных интегральных уравнений Вольтерра третьего рода методом конечных сумм. На основе сингулярно-возмущенного уравнения с использованием квадратурной формулы правых прямоугольников осуществлен переход к системе алгебраических уравнений. Доказана сходимость приближенного решения к точному решению исходного уравнения.

Ключевые слова: интегральные уравнения Вольтерра, квадратурная формула, малый параметр.

Пусть для известных функций р (х) , д (х) , К (х,Ь) линейного интегрального уравнения Вольтерра третьего рода

р(*м х) + 1кшыт = д(Х),

а) р(х) — невозрастающая функция, р(х) Е С2 [0,Ъ] ,д(х) Е С[0,Ъ] ,

р(Ъ) = 0, р(х)> 0 V х Е [0, Ъ), С0р(х) + Cig(х) > 0, 0 0 , D = < (х, t)10 d1>0, G (х) = С0р (х) + С±д (х) + К (х,х) ,d1 = с ons t.

p(x)u(x) + J К(х, t)u(t)dt+C0J p(t)u(t)dt +C0 J J K(s, t)u(t)ds dt +

+Ci f g(t)u(t)dt = Cr J p(t)u2(t)dt + CX J u(t)dt J K(s,t)u(s)ds +

+g(x) + C0 J g(t)dt. (2)

Рассмотрим уравнение с малым параметром £ из интервала (0,1) вида

(е + р(х))и£(х) + J G(t) uE(t)dt = J L(x, t) uE(t)dt + Cr J p(t)u2(t)dt

+С\ J uE(t)dt J K(s, t) u£(s)ds + f(x), (3)

Преобразуем, используя резольвенту ядра — С (0 / (е + р(х)) уравнение (3) к следующему виду [3]

1 г г в (б) \ с(0 г

— J ¿(х,5)и£(5)с?5 — С± J р(Б)ые (Б^йБ + Сг J Щ^йБ J К(у,Б) иЕ(у)с1у

I U£(s)dsJ К (V, Б) и£(у)йу + /СО + X

Доказательство существования единственного непрерывного решения уравнения (4) в шаре радиуса г и равномерной сходимости этого решения к точному решению уравнения (2) приведено в работе [3].

Пусть п — натуральное число, шь — равномерная сетка на отрезке [ 0 , Ь] : шь = = Ш, I = 0..п, Ь = пЩ, Сь — пространство сеточных функций щ = и(х¿) с нормой

п О т + /> + -ехр! -й^- * Рк

! ^ + С] Л ^ + С, И ^ и^ к ^ кк /ис к +Ц, (5)

7 = 1 7 = 1 7 = 1 Л=7′ + 1

+ с0к ^ х; = У^.У = 1. . I, I = 1. . п.

Случай Сх = 0 метода (5) рассмотрен в [2].

Приведем леммы из работы [4, с. 83-84], которые будут использованы в дальнейшем.

Лемма 1. Пусть выполняются условия а)- в^ и функция и (х) 6 С 1 [ 0 , Ь ] . Тогда имеет место оценка

\№[Щ]\\ch Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

-h^LikTle,k — Clh ^ Pk(u£,k + Uk)Ve,k

k=j k=j +1 k = 1 m=j +1

i— 1 L 7 — 1 1 i-1

Z uEk ft ^ Kmkri£jm — Cxft^ r)e]k ft ^ КткиЕт — Cxft ^

X +cih X +^^+Cih Zh Z

^ KkJ иеЛ + euД — fij, 7=1 k=j+l Имеют место следующие оценки i-1 / i C±h v-» / v-» Gk

7 = 1 \ fc=; + l ^ / ^ fc=; + l

Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

откуда следует сходимость данной последовательности.

1. Глушак А. В., Каракеев Т. Т. Численное решение линейной обратной задачи для уравнения Эйлера-Дарбу // Журнал вычислительной математики и математической физики. — 2006. — Т. 46. — № 5. — С. 848-857.

2. Каракеев Т. Т. Численное решение линейных интегральных уравнений Вольтерра третьего рода // Вестник СГТУ. — Самара, 2004. — естествен.-техн. науки. — Вып. 30.

3. Каракеев Т. Т., Бугубаева Ж. Эквивалентное преобразование и регуляризация интегральных уравнений Вольтерра третьего рода // Вестник КНУ. — Бишкек, 2012.

4. Омуров Т. Д., Каракеев Т. Т. Регуляризация и численные методы решения обратных и нелокальных краевых задач. — Бишкек: Илим, 2006. — 164 с.

5. Самарский А. А., Гулин А. В. Численные методы. — Москва: Наука, 1989. — 432 с.

Регуляризация нелинейных интегральных уравнений Вольтерра третьего рода в нерегулярном случае Каракеев Т. Т.1, Рустамова Д.2

1Каракеев Таалайбек Тултемирович / Karakeev Taalaibek Tultemirovich — доктор физико-математических наук, профессор; 2Рустамова Динара /Rustamova Diñara — старший преподаватель, кафедра информатики и вычислительной техники, Кыргызский национальный университет им. Ж. Баласагына, г. Бишкек, Кыргызская Республика

Аннотация: в работе изучаются вопросы регуляризации и единственности решения нелинейных интегральных уравнений Вольтерра третьего рода в случае, когда функциональный коэффициент при искомой функции обращается в нуль на границах интервала области определения решения. Вводится возмущенное уравнение с малым параметром. Доказана равномерная сходимость решения возмущенного уравнения к решению исходного уравнения.

Ключевые слова: уравнение Вольтерра, малый параметр, равномерная сходимость, пространство Гельдера.

Рассмотрим нелинейное интегральное уравнение Вольтерра третьего рода

Po(x)р(x) + J N (x,£p(£))d£ = go( х),

где для известных функций N0 (x, р) = K (x, ^)р(^) + N (x, р),

р = jPi(x) x e[0, bi 1 g(x\ Jgi (x), x e [o, bi ],

0 1^2 (-4 x e[bu bl 0 |g2 (x), x e[bi, b],

а) Pi(x), gi(x)e C[0,bi1 P2(x)e C2[bl,b], Pife^fe) g2 (x) e C[bi, b], gi(bi) = g2 (bi), Pi (0) = P2 (b) = g0(0) = 0, p(x) —

неубывающая функция, pj (x) > 0Vx e (0, b ], P2 (x) — невозрастающая функция,

P2 (x) > 0 Vx e [b, b);

б) K(x,£)e C(D), K(x, x) > 0, C0P0 (x) + K(x, x) > di,

3.1. Вычисление непосредственным суммированием

I. Вычисление с помощью интегральных сумм. Предварительно изучите по учебнику Г М. Фихтенгольца главу XI, п° 176, 177, 180, 184. Обратите особое внимание на примеры, решенные в п° 184.

Способ вычисления определенных интегралов методом суммирования основан на понятии «интегральных сумм», подробно изложенном в п°п° 176, 184.

321. Вычислить интеграл:

Решение. В теоретическом курсе (п° 176) доказывается, что

где f(x) — непрерывная на сегменте Функция, Ii —

точка, произвольно выбранная внутри частичного сегмента , а X—максимальная из длин частичных сегментов. Из определения определенного интеграла следует, что значение

не зависит ни от способа разбиения сегмента На

частичные сегменты Ле от выбора точки

внутри каждого из частичных сегментов. Руководствуясь этим, разобьем сегмент [О, I] на п равных частей. Точками деления сегмента будут:

Получим п частичных сегментов:

Длина каждого из частичных сегментов равна . Заметим, что При

Выберем внутри каждого частичного сегмента наиболее удобное для вычисления положение точек Ii. Пусть это будут самые правые точки каждого частичного сегмента:

Вычислим значение функции /(Ii) в этих точках:

Составим интегральную сумму:

Вычислим предел интегральной суммы при , ,:

Покажем, что и при другом выборе точек Результат будет тот же. В самом деле, пусть в качестве точек взяты точки, являющиеся серединами частичных сегментов:

Вычислим значения функции в этих точках:

Составим интегральную сумму:

Вычислим предел полученной интегральной суммы при стремлении к нулю наибольшего из частичных сегментов:

Полученный предел является значением определенного интеграла.

322. Вычислить интеграл:

Решение. Разобьем отрезок [О, I] на п равных частей точками

Получим п частичных сегментов:

Длина каждого частичного сегмента равна . В качестве точек Выберем самые правые точки частичных сегментов:

Вычислим значения функции В этих точках:

Составим интегральную сумму:

Вычислим предел интегральной суммы при Таким образом,

323. Вычислить интеграл:

Решение. Разсбьем сегмент \ач bI течками деления

и потребуем, чтобы эти точки составляли геометрическую прогрессию

Длины частичных сегментов будут:

В качестве точек Ii выберем самые правые точки

Составим интегральную сумму:

Вычислим предел интегральной суммы при

Вычислим значения функции. _ В этих точках:

324. Вычислить интеграл:

Решение. Для удобства вычислений разобьем сегмент [I, 2] точками На п частичных сегментов так, «чтобы точки деления составляли геометрическую прогрессию. Обозначим через q знаменатель шэогвессии, тогда точки разбиения будут И, следовательно,

Длины частичных сегментов будут:

В качестве точек Выберем самые правые точки

Вычислим значения функции В этих точках:

Составим интегральную сумму:

Вычислим предел интегральной суммы при

Заменим переменную под знаком предела, положив

Тогда И, следовательно, при п-*оо

будет Так как Откуда

325. Вычислить интеграл разбивая сегмент На равные части.

326. Вычислить интеграл Разбивая сегмент На равные части.

327. Вычислить интеграл , разбивая сегмент

Так, чтобы точки деления сегмента составляли геометрическую прогрессию.

328. Вычислить интеграл , разбивая сегмент

Так, чтобы точки деления сегмента составляли геометрическую прогрессию.

329. Вычислить Разбивая сегмент

так, чтобы точки деления сегмента составляли геометрическую прогрессию.

330. Вычислить интеграл , разбивая сегмент

так, чтобы точки деления сегмента составляли геометрическую прогрессию.

2. Вычисление определенных интегралов из геометрических соображений. Предварительно изучите по учебнику Г. М. Фихтенгольца главу X, п° 156 и главу XI, п° 175.

Как известно из теоретического курса (п° 175), определенный интеграл dx численно равен площади кри

волинейнойтрапеции аАВЬ (рис. I), ограниченной сверху кривой Ординатами х = а и х = Ь и отрез

ком оси абсцисс.

331. Используя геометрические соображения, вычислить:

Решение. Обозначив подынтегральную функцию через у, получим: это — окружность радиуса а с центром в начале координат (рис. 2). Подынтегральная функция представляет собой верхнюю половину этой окружности. Так как площадь круга равна То

332. Используя геометрические соображения, вычислить:

Решение. Обозначим подынтегральную функцию через у. Кривая у = sin х изображена на рисунке 3. Разобьем

промежуток интегрирования На два сегмента И

. Из рисунка 3 видно, что кривая Располо

жена на сегменте [0, я] над осью Ох, а на сегменте под осью Ох. Обозначим площади, образуемые данной кривойс осью Ox на этих участках, соответственно через S1 и. Как видно из рисунка 3, численные значения этих площадей равны, но имеют противоположные знаки . Отсюда следует, что

Используя геометрические соображения, вычислить следующие интегралы:

3. Основные свойства определенных интегралов. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XI, п° 180— 183.

341. Оценить интеграл:

Решение. Так как в данной задаче 0 0.

360. Найти точки экстремума и точки перегиба для функции

Решение интегральных уравнений Фредгольма, Вольтера методом конечных сумм

Страницы работы

Содержание работы

Министерство образования и науки Украины

Национальный аэрокосмический университет им. Н.Е. Жуковского «Харьковский авиационный институт»

По курсу «Численные методы»

По теме: «Решение интегральных уравнений»

студент 325 группы

Цель. Решить численно интегральное уравнение Фредгольма, Вольтера методом конечных сумм.

Программная реализация в MathCad.

Исходные данные для уравнения вида ϕ(x) -λ =f(x)

1. Блок формирования весовых коэффициентов.

1. Формула Симпсона.

2. Формула трапеций.

3. Формула правых прямоугольников.

4. Формула левых прямоугольников.

2. Формирование матрицы коэффициентов для уравнения Фредгольма, Вольтера.

3. Вычисление значений f(х) (правой части уравнения) в узловых точках.

Значения источника в узловых точках:

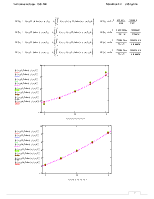
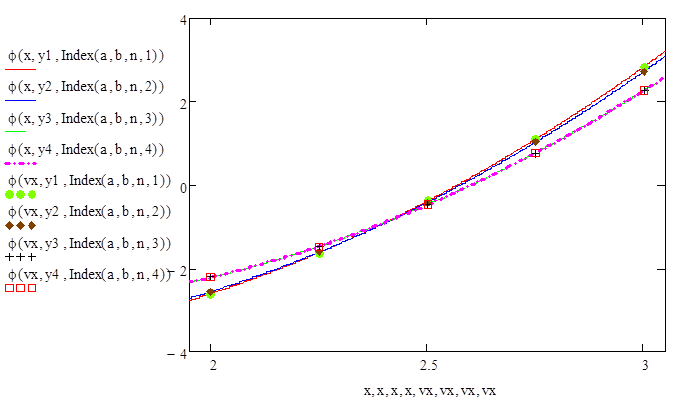
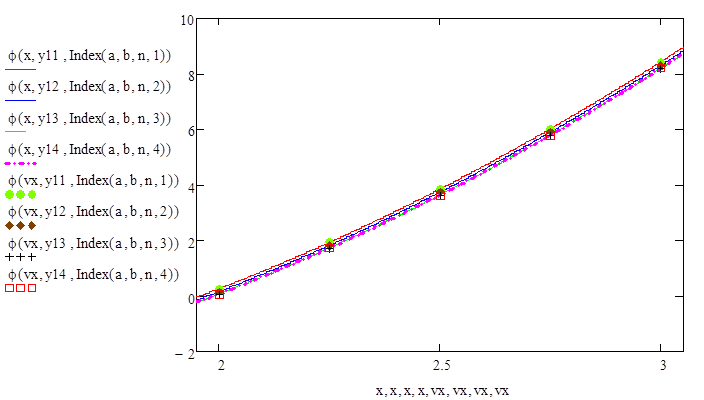
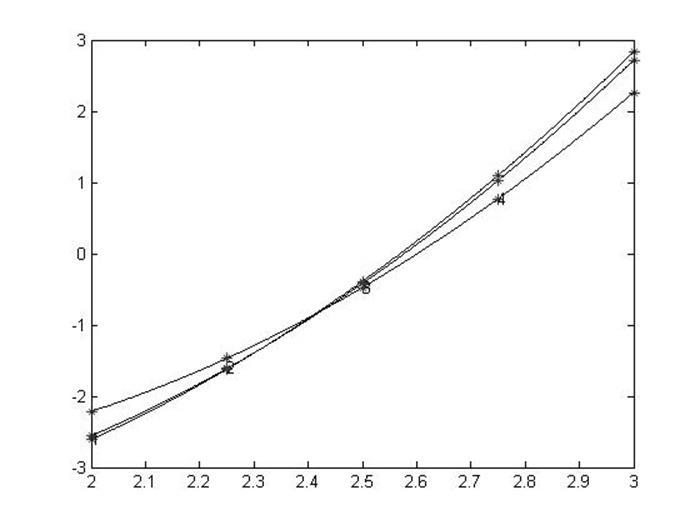
Вычисляем значения искомой функции в узловых точках: ϕ(vx(i))

Искомую функцию ɸ(х) запишем в виде :

Проверка результатов вычислений.

function res = Integral_equation(a,b,n,N,str);

lambda = 8; % параметр

%1. Табулирование значений

%2. Формируем весовые коэффициенты для формулы N

A = zeros(n,1);%матрица весовых коэффициентов

switch (N) %формула Симпсона

case 2 %формула трапеций

case <3, 4>%формулы правых и левых прямоугольников

otherwise error(‘This is impossible value’)

%3. Формирование матрицы коэффициентов

case ‘Fredgolm’% для уравнения Фредгольма

if (i == j) D(i,j) = 1-lambda*A(j)*k(vx(i),vx(j));

else D(i,j) = -lambda*A(j)*k(vx(i),vx(j));

case ‘Volter’% Вольтера

% 4. Вычисление значений искомой функции в узловых точках

% 5. Построение графика искомой функции fi(х) на интервале [a,b];

plot(X,VR,’-k’),hold on,plot(vx,y,’*r’),hold on;

% 6. Проверка вычислений. left side of equation

G = fi(x,lambda,y,vx,A) — lambda*int(k(x,t)*fi(t,lambda,y,vx,A),t,a,b)

function res = F(x);

% источник интегрального уравнения

function res = fi(x,lambda,y,vx,A);

Int = Int + A(i)*k(x,vx(i))*y(i);

res = F(x)+ lambda*Int;

function res = k(x,t);

% ядро интегрального уравнения

Похожие материалы

Информация о работе

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).