Метод трапеций
Вы будете перенаправлены на Автор24
Метод трапеций — это метод приближённого интегрирования, полезный в тех случаях, когда нет возможности найти первообразную функции и вычислить интеграл через неё.
Помимо метода трапеций существуют другие методы приближённого интегрирования, например, метод прямоугольников и метод парабол.
Метод трапеций по сути похож на метод прямоугольников, но при этом он менее точный, чем метод средних прямоугольников.
Сущность метода трапеций
Рисунок 1. Метод трапеций для вычисления интегралов
Предположим, требуется вычислить интеграл от функции $f(x)$ на отрезке $\left[a;b\right]$.
Также как и в случае с методом прямоугольников разобьём график кривой на элементарные сегменты c помощью точек с абсциссами $x_i$, и получим ломаную с вершинами в точках $(x_i;y_i)$, при этом $y_i=f(x_i)$, а $i$ принимает значения от $0$ до $n-1$.
Для этого выберем количество отрезков, на которые разбиваем исследуемый интервал и воспользуемся формулой для вычисления длины одного такого отрезка, которую мы уже использовали для метода прямоугольников:
Для вычисления по методу трапеций между собой соединяются две рядом стоящие точки разбиения, в результате образуя элементарные сегменты. Как видно дальше, значение функции $f(x)$ берётся на границах исследуемого отрезка.
Площадь первой такой трапеции составит:
а площадь $i$-ой трапеции составит:
Сложим площади всех элементарных трапеций:
Таким образом, площади всех элементарных трапеций, сложенные вместе, являются приближённой площадью фигуры, ограниченной линиями $x=a$, $x=b$, осью абсцисс и графиком кривой $f(x)$.
Готовые работы на аналогичную тему
Формула для приближённого вычисления интеграла методом трапеций:
Погрешность при использовании метода трапеций
Погрешность метода составляет:
Как видно из вышеприведённой формулы, здесь погрешность несколько больше чем погрешность метода средних прямоугольников, однако, не всегда удобно использовать именно этот метод. Метод трапеции удобен если самого графика функции нет, но есть значения, которые принимает функция $f(x)$ в точках разбиения. В случаях же когда всё же есть график, целесообразнее пользоваться методом средних прямоугольников.
Также при невозможности определения максимума функции сложно определить вычисляемую погрешность. В этом случае можно прибегнуть к следующему: сначала провести численное интегрирование методом трапеций для $n=10$, а затем на том же отрезке провести вычисление при $n=20$. Если разница двух полученных значений интегралов составляет меньше чем требуемая по условию погрешность, то в качестве ответа выбирают приближённое значение интеграла при $n=20$, а вычисления заканчивают. В противном случае если требуемая точность не достигнута, продолжают удваивать дальше количество отрезков.
Посчитайте интеграл $\int_1^2 \frac
Разобьём нашу функцию на 10 равных сегментов.
В начале оценим погрешность вычисления:
В данном случае погрешность составляет $|δ_n|≤0.00008$, следовательно, для разбиения можно использовать 10 сегментов.
Также как и с методом прямоугольников, разобьём подынтегральную функцию на 10 отрезков, длина каждого из которых $Δx=\frac<2-1><10>=0,1$ и вычислим значение подынтегральной функции $y(x)=\frac<1>
Сумма всех вычисленных значений функции $f(x)$ от первого до девятого включительно составит $6.1877$, а само значение интеграла составит:
Данное значение отвечает необходимой точности.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 21 02 2022
Метод трапеций
Сегодня мы познакомимся с еще одним методом численного интегрирования, методом трапеций. С его помощью мы будем вычислять определенные интегралы с заданной степенью точности. В статье мы опишем суть метода трапеций, разберем, как выводится формула, сравним метод трапеции с методом прямоугольника, запишем оценку абсолютной погрешности метода. Каждый из разделов мы проиллюстрируем примерами для более глубокого понимания материала.
Метод трапеций
Предположим, что нам нужно приближенно вычислить определенный интеграл ∫ a b f ( x ) d x , подынтегральная функция которого y = f ( x ) непрерывна на отрезке [ a ; b ] . Для этого разделим отрезок [ a ; b ] на несколько равных интервалов длины h точками a = x 0 x 1 x 2 . . . x n — 1 x n = b . Обозначим количество полученных интервалов как n .
Найдем шаг разбиения: h = b — a n . Определим узлы из равенства x i = a + i · h , i = 0 , 1 , . . . , n .
На элементарных отрезках рассмотрим подынтегральную функцию x i — 1 ; x i , i = 1 , 2 , . . , n .
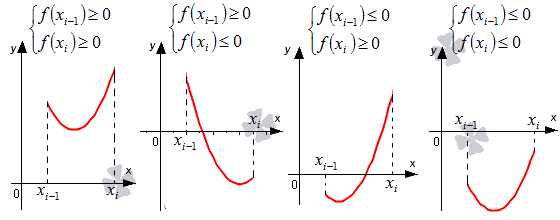
При бесконечном увеличении n сведем все случаи к четырем простейшим вариантам:
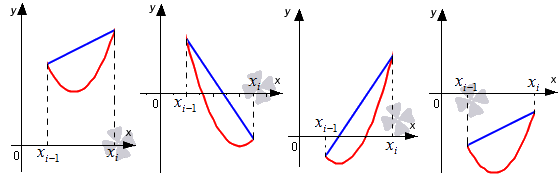
Выделим отрезки x i — 1 ; x i , i = 1 , 2 , . . . , n . Заменим на каждом из графиков функцию y = f ( x ) отрезком прямой, который проходит через точки с координатами x i — 1 ; f x i — 1 и x i ; f x i . Отметим их на рисунках синим цветом.
Возьмем выражение f ( x i — 1 ) + f ( x i ) 2 · h в качестве приближенного значения интеграла ∫ x i — 1 x i f ( x ) d x . Т.е. примем ∫ x i — 1 x i f ( x ) d x ≈ f ( x i — 1 ) + f ( x i ) 2 · h .
Давайте посмотрим, почему метод численного интегрирования, который мы изучаем, носит название метода трапеций. Для этого нам нужно выяснить, что с точки зрения геометрии означает записанное приближенное равенство.
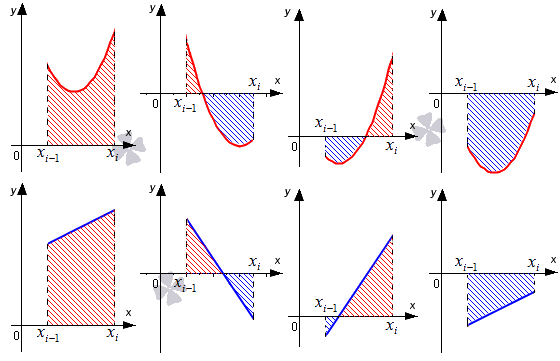
Для того, чтобы вычислить площадь трапеции, необходимо умножить полусуммы ее оснований на высоту. В первом случае площадь криволинейной трапеции примерно равна трапеции с основаниями f ( x i — 1 ) , f ( x i ) высотой h . В четвертом из рассматриваемых нами случаев заданный интеграл ∫ x i — 1 x f ( x ) d x приближенно равен площади трапеции с основаниями — f ( x i — 1 ) , — f ( x i ) и высотой h , которую необходимо взять со знаком « — ». Для того, чтобы вычислить приближенное значение определенного интеграла ∫ x i — 1 x i f ( x ) d x во втором и третьем из рассмотренных случаев, нам необходимо найти разность площадей красной и синей областей, которые мы отметили штриховкой на расположенном ниже рисунке.
Подведем итоги. Суть метода трапеций заключается в следующем: мы можем представить определенный интеграл ∫ a b f ( x ) d x в виде суммы интегралов вида ∫ x i — 1 x i f ( x ) d x на каждом элементарном отрезке и в последующей приближенной замене ∫ x i — 1 x i f ( x ) d x ≈ f ( x i — 1 ) + f ( x i ) 2 · h .
Формула метода трапеций
Вспомним пятое свойство определенного интеграла: ∫ a b f ( x ) d x = ∑ i = 1 n ∫ x i — 1 x i f ( x ) d x . Для того, чтобы получить формулу метода трапеций, необходимо вместо интегралов ∫ x i — 1 x i f ( x ) d x подставить их приближенные значения: ∫ x i — 1 x i f ( x ) d x = ∑ i = 1 n ∫ x i — 1 x i f ( x ) d x ≈ ∑ i = 1 n f ( x i — 1 ) + f ( x i ) 2 · h = = h 2 · ( f ( x 0 ) + f ( x 1 ) + f ( x 1 ) + f ( x 2 ) + f ( x 2 ) + f ( x 3 ) + . . . + f ( x n ) ) = = h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n ) ⇒ ∫ x i — 1 x i f ( x ) d x ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n )
Формула метода трапеций: ∫ x i — 1 x i f ( x ) d x ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n )
Оценка абсолютной погрешности метода трапеций
Оценим абсолютную погрешность метода трапеций следующим образом:
δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) · n · h 3 12 = m a x x ∈ [ a ; b ] f » ( x ) · b — a 3 12 n 2
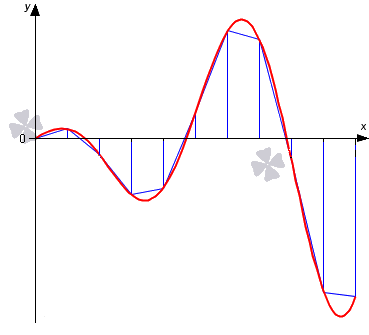
Графическая иллюстрация метода трапеций
Графическая иллюстрация метода трапеций приведена на рисунке:
Примеры вычислений
Разберем примеры использования метода трапеций для приближенного вычисления определенных интегралов. Особое внимание уделим двум разновидностям заданий:
- вычисление определенного интеграла методом трапеций для данного числа разбиения отрезка n;
- нахождение приближенного значения определенного интеграла с оговоренной точностью.
При заданном n все промежуточные вычисления необходимо проводить с достаточно высокой степенью точности. Точность вычислений должна быть те выше, чем больше n .
Если мы имеем заданную точность вычисления определенного интеграла, то все промежуточные вычисления необходимо проводить на два и более порядков точнее. Например, если задана точность до 0 , 01 , то промежуточные вычисления мы проводим с точностью до 0 , 0001 или 0 , 00001 . При больших n промежуточные вычисления необходимо проводить с еще более высокой точностью.
Рассмотрим приведенное выше правило на примере. Для этого сравним значения определенного интеграла, вычисленного по формуле Ньютона-Лейбница и полученного по методу трапеций.
Итак, ∫ 0 5 7 d x x 2 + 1 = 7 a r c t g ( x ) 0 5 = 7 a r c t g 5 ≈ 9 , 613805 .
Вычислим по методу трапеций определенный интеграл ∫ 0 5 7 x 2 + 1 d x для n равным 10 .
Решение
Формула метода трапеций имеет вид ∫ x i — 1 x i f ( x ) d x ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n )
Для того, чтобы применить формулу, нам необходимо вычислить шаг h по формуле h = b — a n , определить узлы x i = a + i · h , i = 0 , 1 , . . . , n , вычислить значения подынтегральной функции f ( x ) = 7 x 2 + 1 .
Шаг разбиения вычисляется следующим образом: h = b — a n = 5 — 0 10 = 0 . 5 . Для вычисления подынтегральной функции в узлах x i = a + i · h , i = 0 , 1 , . . . , n будем брать четыре знака после запятой:
i = 0 : x 0 = 0 + 0 · 0 . 5 = 0 ⇒ f ( x 0 ) = f ( 0 ) = 7 0 2 + 1 = 7 i = 1 : x 1 = 0 + 1 · 0 . 5 = 0 . 5 ⇒ f ( x 1 ) = f ( 0 . 5 ) = 7 0 , 5 2 + 1 = 5 , 6 . . . i = 10 : x 10 = 0 + 10 · 0 . 5 = 5 ⇒ f ( x 10 ) = f ( 5 ) = 7 5 2 + 1 ≈ 0 , 2692
Внесем результаты вычислений в таблицу:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x i | 0 | 0 . 5 | 1 | 1 , 5 | 2 | 2 , 5 | 3 | 3 , 5 | 4 | 4 , 5 | 5 |
| f ( x i ) | 7 | 5 , 6 | 3 , 5 | 2 , 1538 | 1 , 4 | 0 , 9655 | 0 , 7 | 0 , 5283 | 0 , 4117 | 0 , 3294 | 0 , 2692 |
Подставим полученные значения в формулу метода трапеций: ∫ 0 5 7 d x x 2 + 1 ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n ) = = 0 , 5 2 · 7 + 2 · 5 , 6 + 3 , 5 + 2 , 1538 + 1 , 4 + 0 , 9655 + 0 , 7 + 0 , 5283 + 0 , 4117 + 0 , 3294 + 0 , 2692 = 9 , 6117
Сравним наши результаты с результатами, вычисленными по формуле Ньютона-Лейбница. Полученные значения совпадают до сотых.
Ответ: ∫ 0 5 7 d x x 2 + 1 = 9 , 6117
Вычислим по методу трапеций значение определенного интеграла ∫ 1 2 1 12 x 4 + 1 3 x — 1 60 d x с точностью до 0 , 01 .
Решение
Согласно условию задачи a = 1 ; b = 2 , f ( x ) = 1 12 x 4 + 1 3 x — 1 60 ; δ n ≤ 0 , 01 .
Найдем n , которое равно количеству точек разбиения отрезка интегрирования, с помощью неравенства для оценки абсолютной погрешности δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) · ( b — a ) 3 12 n 2 . Сделаем мы это следующим образом: мы найдем значения n , для которых будет выполняться неравенство m a x x ∈ [ a ; b ] f » ( x ) · ( b — a ) 3 12 n 2 ≤ 0 , 01 . При данных n формула трапеций даст нам приближенное значение определенного интеграла с заданной точностью.
Для начала найдем наибольшее значение модуля второй производной функции на отрезке [ 1 ; 2 ] .
f ‘ ( x ) = 1 12 x 4 + 1 3 x — 1 60 ‘ = 1 3 x 3 + 1 3 ⇒ f » ( x ) = 1 3 x 3 + 1 3 ‘ = x 2
Вторая производная функция является квадратичной параболой f » ( x ) = x 2 . Из ее свойств мы знаем, что она положительная и возрастает на отрезке [ 1 ; 2 ] . В связи с этим m a x x ∈ [ a ; b ] f » ( x ) = f » ( 2 ) = 2 2 = 4 .
В приведенном примере процесс нахождения m a x x ∈ [ a ; b ] f » ( x ) оказался достаточно простым. В сложных случаях для проведения вычислений можно обратиться к наибольшим и наименьшим значениям функции. После рассмотрения данного примера мы приведем альтернативный метод нахождения m a x x ∈ [ a ; b ] f » ( x ) .
Подставим полученное значение в неравенство m a x x ∈ [ a ; b ] f » ( x ) · ( b — a ) 3 12 n 2 ≤ 0 , 01
4 · ( 2 — 1 ) 3 12 n 2 ≤ 0 , 01 ⇒ n 2 ≥ 100 3 ⇒ n ≥ 5 , 7735
Количество элементарных интервалов, на которые разбивается отрезок интегрирования n является натуральным числом. Для поведения вычислений возьмем n равное шести. Такое значение n позволит нам достичь заданной точности метода трапеций при минимуме расчетов.
Вычислим шаг: h = b — a n = 2 — 1 6 = 1 6 .
Найдем узлы x i = a + i · h , i = 1 , 0 , . . . , n , определим значения подынтегральной функции в этих узлах:
i = 0 : x 0 = 1 + 0 · 1 6 = 1 ⇒ f ( x 0 ) = f ( 1 ) = 1 12 · 1 4 + 1 3 · 1 — 1 60 = 0 , 4 i = 1 : x 1 = 1 + 1 · 1 6 = 7 6 ⇒ f ( x 1 ) = f 7 6 = 1 12 · 7 6 4 + 1 3 · 7 6 — 1 60 ≈ 0 , 5266 . . . i = 6 : x 10 = 1 + 6 · 1 6 = 2 ⇒ f ( x 6 ) = f ( 2 ) = 1 12 · 2 4 + 1 3 · 2 — 1 60 ≈ 1 , 9833
Результаты вычислений запишем в виде таблицы:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x i | 1 | 7 6 | 4 3 | 3 2 | 5 3 | 11 6 | 2 |
| f x i | 0 , 4 | 0 , 5266 | 0 , 6911 | 0 , 9052 | 1 , 1819 | 1 , 5359 | 1 , 9833 |
Подставим полученные результаты в формулу трапеций:
∫ 1 2 1 12 x 4 + 1 3 x — 1 60 d x ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n ) = = 1 12 · 0 , 4 + 2 · 0 , 5266 + 0 , 6911 + 0 , 9052 + 1 , 1819 + 1 , 5359 + 1 , 9833 ≈ 1 , 0054
Для проведения сравнения вычислим исходный интеграл по формуле Ньютона-Лейбница:
∫ 1 2 1 12 x 4 + 1 3 x — 1 60 d x = x 5 60 + x 2 6 — x 60 1 2 = 1
Как видим, полученной точности вычислений мы достигли.
Ответ: ∫ 1 2 1 12 x 4 + 1 3 x — 1 60 d x ≈ 1 , 0054
Для подынтегральных функций сложного вида нахождение числа n из неравенства для оценки абсолютной погрешности не всегда просто. В этом случае будет уместен следующий метод.
Обозначим приближенное значение определенного интеграла, которое было получено по методу трапеций для n узлов, как I n . Выберем произвольное число n . По формуле метода трапеций вычислим исходный интеграл при одинарном ( n = 10 ) и удвоенном ( n = 20 ) числе узлов и найдем абсолютную величину разности двух полученных приближенных значений I 20 — I 10 .
Если абсолютная величина разности двух полученных приближенных значений меньше требуемой точности I 20 — I 10 δ n , то мы прекращаем вычисления и выбираем значение I 20 , которое можно округлить до требуемого порядка точности.
Если абсолютная величина разности двух полученных приближенных значений больше требуемой точности, то необходимо повторить действия с удвоенным количеством узлов ( n = 40 ) .
Такой метод требует проведения большого объема вычислений, поэтому разумно использовать вычислительную технику для экономии времени.
Решим с помощью приведенного выше алгоритма задачу. С целью экономии времени опустим промежуточные вычисления по методу трапеций.
Необходимо вычислить определенный интеграл ∫ 0 2 x e x d x по методу трапеций с точностью до 0 , 001 .
Решение
Возьмем n равное 10 и 20 . По формуле трапеций получим I 10 = 8 , 4595380 , I 20 = 8 , 4066906 .
I 20 — I 10 = 8 , 4066906 — 8 , 4595380 = 0 , 0528474 > 0 , 001 , что требует продолжения вычислений.
Возьмем n равное 40 : I 40 = 8 , 3934656 .
I 40 — I 20 = 8 , 3934656 — 8 , 4066906 = 0 , 013225 > 0 , 001 , что также требует продолжения вычислений.
Возьмем n равное 80 : I 80 = 8 , 3901585 .
I 80 — I 40 = 8 , 3901585 — 8 , 3934656 = 0 , 0033071 > 0 , 001 , что требует проведения еще одного удвоения числа узлов.
Возьмем n равное 160 : I 160 = 8 , 3893317 .
I 160 — I 80 = 8 , 3893317 — 8 , 3901585 = 0 , 0008268 0 , 001
Получить приближенное значение исходного интеграла можно округлив I 160 = 8 , 3893317 до тысячных: ∫ 0 2 x e x d x ≈ 8 , 389 .
Для сравнения вычислим исходный определенный интеграл по формуле Ньютона-Лейбница: ∫ 0 2 x e x d x = e x · ( x — 1 ) 0 2 = e 2 + 1 ≈ 8 , 3890561 . Требуемая точность достигнута.
Ответ: ∫ 0 2 x e x d x ≈ 8 , 389
Погрешности
Промежуточные вычисления для определения значения определенного интеграла проводят в большинстве своем приближенно. Это значит, что при увеличении n начинает накапливаться вычислительная погрешность.
Сравним оценки абсолютных погрешностей метода трапеций и метода средних прямоугольников:
δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) n · h 3 12 = m a x x ∈ [ a ; b ] f » ( x ) · b — a 3 12 n 2 δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) n · h 3 24 = m a x x ∈ [ a ; b ] f » ( x ) · b — a 3 24 n 2 .
Метод прямоугольников для заданного n при одинаковом объеме вычислительной работы дает вдвое меньшую погрешность. Это делает метод более предпочтительным в тех случаях, когда известны значения функции в средних отрезках элементарных отрезков.
В тех случаях, когда интегрируемые функции задаются не аналитически, а в виде множества значений в узлах, мы можем использовать метод трапеций.
Если сравнивать точность метода трапеций и метода правых и левых прямоугольников, то первый метод превосходит второй в точности результата.
C++ и Численные Методы: Приближенное интегрование по Ньютону-Котесу
Методы Ньютона-Котеса — это совокупность техник приближенного интегрирования, основанных на:
- разбиении отрезка интегрирования на равные промежутки;
- аппроксимации подинтегральной функции на выбранных промежутках многочленами;
- нахождении суммарной площади полученных криволинейных трапеций.
В этой статье будут рассмотрены несколько методов Ньютона-Котеса:
- метод трапеций;
- метод Симпсона;
- метод Ромберга.
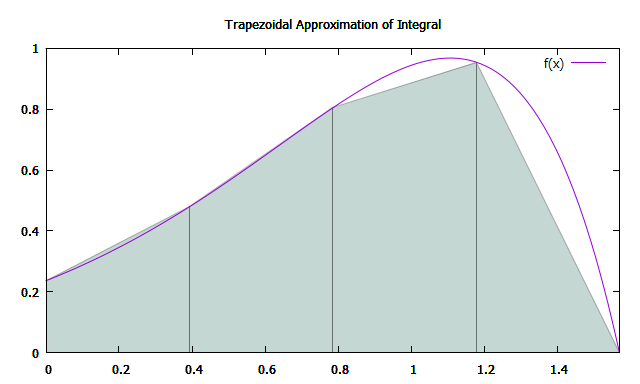
Метод трапеций
Метод трапеций — простейший из рассмотренных. В качестве примера возьмем следующий интеграл:
Точность приближения зависит от числа N отрезков, на которые разбивается промежуток интегрирования. Таким образом, длина промежутка:
Площадь трапеции может быть вычислена по формуле:
Суммируя все вышесказанное, приближенное значение интеграла вычисляется по формуле:
Функция, вычисляющая интеграл методом трапеций должна принимать 4 параметра:
- границы отрезка интегрирования;
- подинтегральную функцию;
- число N промежутков разбиения.
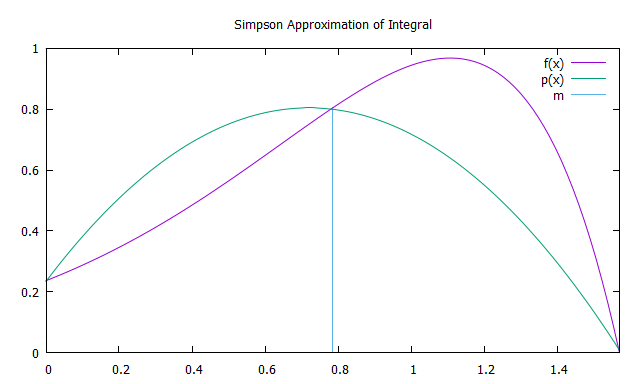
Метод Симпсона
Метод Симпсона заключается в интегрировании интерполяционного многочлена второй степени функции f(x) с узлами интерполяции a, b и m = (a+b)/2 — параболы p(x).Для повышения точности имеет смысл разбить отрезок интегрирования на N равных промежутков(по аналогии с методом трапеций), на каждом из которых применить метод Симпсона.
Площадь параболы может быть найдена суммированием площадей 6 прямоугольников равной ширины. Высота первого из них должна быть равна f(a), с третьего по пятый — f(m), шестого — f(m). Таким образом, приближение методом Симпсона находим по формуле:
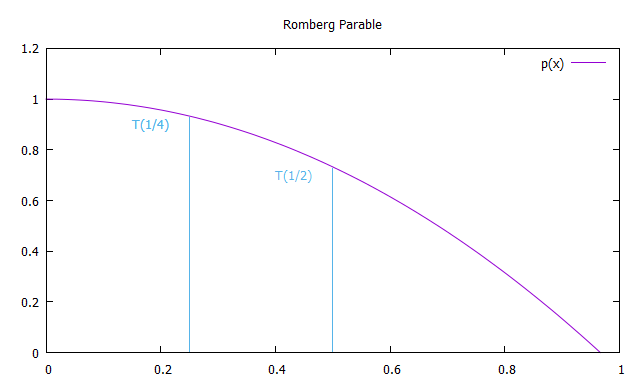
Метод Ромберга
Пусть T(x) — приближение интеграла, полученное методом трапеций с шагом x. Получим 3 таких приближения, уменьшая размер шага в 2 раза при каждом вычислении.
Построим теперь симметричную относительно оси y параболу, проходящую через точки T(1) и T(1/2) чтоб экстраполировать полученные значения для x стремящегося к 0.
Следовательно, каждый член первого столбца R(n, 0) приближений Ромберга эквивалентен решениям полученным методом трапеций, а каждое решение второго столбца R (n, 1) — методом Симпсона. Таким образом, формулы для приближенного интегрирования методом Ромберга:
http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/metod-trapetsij/
http://habr.com/ru/post/479202/