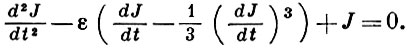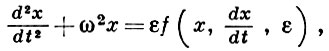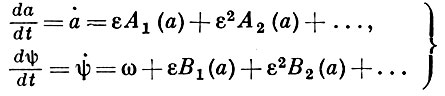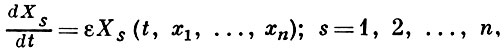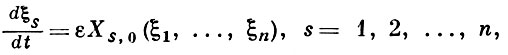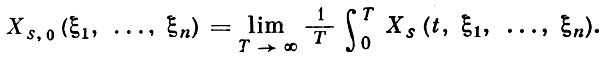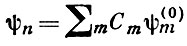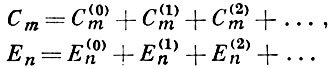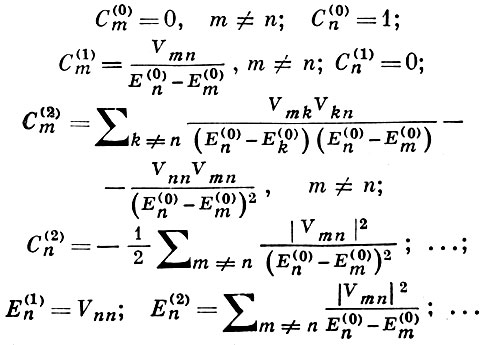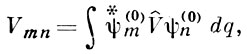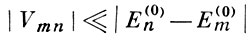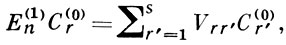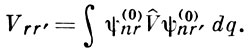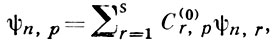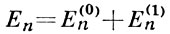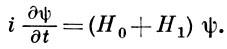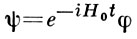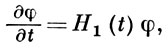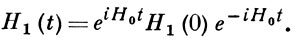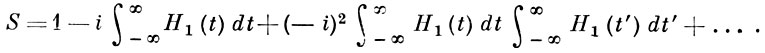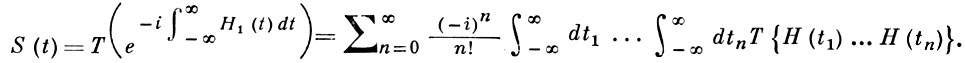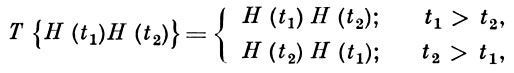Метод возмущений дифференциальные уравнения с малым параметром

Дифференциальные уравнения с малым параметром при производной

Возьмем дифференциальное уравнение (где — параметр)

Если функция в некоторой замкнутой области изменения непрерывна по совокупности аргументов и удовлетворяет условию Липшица по

где не зависит от , то решение (1) непрерывно зависит от .

Во многих задачах физики приходится рассматривать уравнения вида (где — малый параметр)

Разделив обе части уравнения (2) на , приведем его к виду

откуда видно, что правая часть (3) терпит разрыв при , так что теоремой о непрерывной зависимости решений от параметра воспользоваться в этом случае нельзя.

Вопрос ставится так: при каких условиях для малых значений в уравнении (2) можно отбросить член и в качестве приближения к решению дифференциального уравнения (2) рассматривать решение так называемого «вырожденного уравнения»

Пусть для определенности 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> и пусть вырожденное уравнение (4) имеет лишь одно решение . В зависимости от поведения вблизи решения уравнения (4) решение дифференциального уравнения (2) при стремится к решению вырожденного уравнения, либо быстро удаляется от него.

В первом случае решение уравнения (4) называют устойчивым , во втором — неустойчивым .

Именно, если при переходе через график решения вырожденного уравнения (4) функция с возрастанием при фиксированном меняет знак с на , то решение вырожденного уравнения устойчиво и им можно приближенно заменить решение . уравнения (2) (рис. 47).

Если же функция меняет знак с на , то решение вырожденного уравнения (4) неустойчиво и заменять решение дифференциального уравнения (2) решением вырожденного уравнения (4) нельзя (рис. 48).

Достаточные условия устойчивости или неустойчивости выражаются следующими предложениями.

1. Если на решении уравнения (4), то решение вырожденного уравнения устойчиво.

2. Если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAG0AAAAuBAMAAADQGoqnAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAnpQBwUdnMSEQgeDwsdDVhGY9AAAC90lEQVRIx61UTUhUURT+nDs/b6yRcVNCQdIPES66MOgirRnyJ8zISW0RJDObQJzFzNCsgnCMatNiJoso0pqFpERhqAVuGkgTFMyCWoUpSUEbw0atrKRz541vRl5XfdBdvHvfOee755zvnHuA/7Ps0bX/0fWMyx7ExaZ4gZuhtarW9Xwcb3gp9u6PQPVaFTvsl+PMfn6W4rEtLcBaCVgTOTrlhxwXm4G7GDCletBJoW715CoL5biOEArItmAWCDCgLdcffHE58EKvOwW4ncAUpRQ8n8mNM05SrxTW9bnZV4nI18FiNg68TVap5Hf3XySiCoqldM5x++Rr8tMItgi4Jlxpcb7//tg0h9kjw5nIuJ7oPhiHZVHQqoovI7ZngrSVUjoHwCYptDqkcWXfVfFtBEVq+SkZLuiEskA0/FFxDs1wF18Px/r8KBPxLVOqtFd4bKqcDYJOjlmpPy/uOlVfbEmUrwth6lJfyzfRnVJeWGfCPkf7oZ90Pkq4M8fQ9wTsUfiFrRYoT8j82Z6fEDqzCKibwzQSQmSY+KyJTBFbMXndFdEgrEIUOEZdRWwwQT4XJwS4zr60MednZ5t4eXlqVIpTy+KZDmbtL8k+UvbqcRowpL4sTVE6o8P5vNax7F/TgfTWnP5e0cTXMjdYejXRe7DlrD81DWZN0+DS5D3avUWrliNgK/qkXbJyNW3PsLgAVs8NjLpmdfZYjOLQXs1VHAjHGnZvtLTL25/m+DtVuNHScJc+ifYiXJKvErmpOGuELSPcLyPphau1+s0bgDW9W+2XkFU/jFt7ZLAirT9HA7rhf29f4N9zz1KU7YyrLTr1XiijG0asbyk2ycVYM77OZaaY0WV76K+PshvS7patktOtSR6pC38IGYLlDcH8W6k1LfkShnBBP/Ln80KOVMCQP5aMwkHjt9xjkJUVwgzQNDQWJSzUrz6/PR702uJGcArNqZN8y/A0P2KsiDvi17/AvT95Z5uxQDtGxuOwvrlV5TVYdxfH5nrlL0fPxey1y4iJAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> на решении уравнения (4), то решение вырожденного уравнения неустойчиво.

Если вырожденное уравнение (4) имеет несколько решений , то каждое из них должно быть исследовано на устойчивость . При этом поведение интегральных кривых дифференциального уравнения (2) при может быть различным в зависимости от выбора начальных условий — начальной точки .

Возможен также полуустойчивый случай , когда функция при переходе через кривую не меняет знак (например, если есть корень четной кратности вырожденного уравнения (4)). В этом случае при малом интегральные кривые уравнения (2) с одной стороны кривой стремятся к этой кривой, а с другой — удаляются от нее.

В первом случае мы говорили, что начальная точка принадлежит области притяжения полуустойчивого решения , а во втором случае — области отталкивания.

В полуустойчивом случае, как правило, нельзя заменять решение исходного уравнения (2) решением вырожденного уравнения (4).

Можно указать критерии, когда интегральные кривые уравнения (2) при соответствующем выборе начальной точки приближаются к решению вырожденного уравнения и остаются в его окрестности при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, однако это справедливо лишь при отсутствии возмущений уравнения (2).

Приведем эти критерии.

Пусть в окрестности полуустойчивого решения вырожденного уравнения (4) функция . Если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAE4AAAAYBAMAAACmU9bEAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAQcWdZ4ER4PAxIVGx9LHpLAAAAYVJREFUKM+1kz9LAzEYxp/z2t4fr3CKoEuhWqyrVtBBhKIdughHBSeFji4FERXFpRRxcak6SqEfoTg5iri49cATi/hdfPMmuVYtIoiBJG+SX+7N8yQH/E+x53/HZYrUrIjIq/7E7dCqGYjIyX9bHOuHOaqTVG+Aza/Y3eJJHL9RPaC6D9TanzH3AmU9ZewBiToljSg9S7qOabOLtFaZJBnePbGh5GlnToNWFiNZ4BJYe0qRDDtAshJtwe3JFA++5NLEdYE8zMaxGNc6MKamafFZnasgwQxziQDjVUvMZKhpCWsiLWC5qLkQXpu+6GluQwSzsdJKJ+YsGAE1ilvVXnJJMVfjvDbMNtbFbMtn+wbyFjivTVwdI4GF0XPW1YEbpbIxpzB47J/TKEzMNdmnAEZoEhxKX5RcmuQjXb2/LknfyeeZR/L5Rfrs62OWS2eiO1QPyaB7MKqSH7w3uCUROz09PpXdrj/05dE1q3Iru+3hL1TcsdrB+pyj4ZzTf+cLvK/5l//sA8btRxt561mKAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, то интегральные кривые уравнения (2), приближающиеся к кривой , не могут пересечь эту кривую и остаются в ее окрестности при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> (начальная точка должна находиться в области притяжения полуустойчивого решения ; если находится в области отталкивания, то соответствующая интегральная кривая уравнения (2) быстро удаляется от кривой ) (рис. 49). Если , то интегральные кривые, приближающиеся к графику функции , пересекут его и с другой стороны кривой быстро удалятся от нее. Если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAE4AAAAYBAMAAACmU9bEAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAQcWdZ4ER4PAxIVGx9LHpLAAAAYVJREFUKM+1kz9LAzEYxp/z2t4fr3CKoEuhWqyrVtBBhKIdughHBSeFji4FERXFpRRxcak6SqEfoTg5iri49cATi/hdfPMmuVYtIoiBJG+SX+7N8yQH/E+x53/HZYrUrIjIq/7E7dCqGYjIyX9bHOuHOaqTVG+Aza/Y3eJJHL9RPaC6D9TanzH3AmU9ZewBiToljSg9S7qOabOLtFaZJBnePbGh5GlnToNWFiNZ4BJYe0qRDDtAshJtwe3JFA++5NLEdYE8zMaxGNc6MKamafFZnasgwQxziQDjVUvMZKhpCWsiLWC5qLkQXpu+6GluQwSzsdJKJ+YsGAE1ilvVXnJJMVfjvDbMNtbFbMtn+wbyFjivTVwdI4GF0XPW1YEbpbIxpzB47J/TKEzMNdmnAEZoEhxKX5RcmuQjXb2/LknfyeeZR/L5Rfrs62OWS2eiO1QPyaB7MKqSH7w3uCUROz09PpXdrj/05dE1q3Iru+3hL1TcsdrB+pyj4ZzTf+cLvK/5l//sA8btRxt561mKAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> при и при t_1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAAaiFwGEw00IhQBBx8FF4mUoDAAAAxElEQVQY02NgwANOo/HZHkAZPN/QZNgLoAyhjyAydANcRl4BypAFM1iL4VL9ARB6sb3zAhAtWjwBIhDsrwxhzdCPgDDknCB0R3kHVLuuANQUDqcEEMX4CUhkgxiX4FZzqICkOL4yMBj9Arn+D1yGEyzD/JOBIfEXinc4XBpAlAjQO4wgGaaPzBBXSkBdIK8gLgCWYXFIAguwFkFdnW9gA9HDelkb4tMJsDApMYDIMEyD+A8ROtlQe7AC3DLm3x1waAEFCwDPjC4HC7XnhAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, то при достаточно малом интегральные кривые, выходящие из точки , принадлежащей области притяжения корня , остаются вблизи кривой при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» />; в окрестности точки они пересекают кривую и затем удаляются от нее.

Если в окрестности полуустойчивого решения функция , то для справедливости высказанных утверждений знаки у производной надо заменить противоположными.

Пример 1. Выяснить, стремится ли решение уравнения

удовлетворяющее начальному условию к решению вырожденного уравнения при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> и .

Решение. Имеем , так что решение вырожденного уравнения устойчиво и, следовательно, решение исходного уравнения , выходящее из любой начальной точки , стремится к решению вырожденного уравнения при и t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> (рис.50).

В этом можно убедиться непосредственно проверкой. Решая дифференциальное уравнение (5) как линейное неоднородное при заданном начальном условии , найдем

откуда непосредственно видно, что при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, то есть 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAFQAAAATCAMAAAA56NonAAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEXRSTlMA2FEQQYEhAcCcYYIx8LBwQH4YNZwAAAErSURBVDjLzZTZEoMgDEVZEkgQ0Pz/zxbUcSlo7Uwfmgd0HDjm3oQo9ffhIfr11Yb7rSY+ZEJi1uvmUdzdViv4jOlSyS6kBUba3yYqpj3PnTxYCscLz0Ysj8tgse3HibgxRVOF1hQBWQjhUjuiTtjTD0xwUuhlgZZ8HbAYuDTVghGGfqUckzlg3Q59bClMtoPVYTsMQnOFBM6WGtzDni2lYHSrx9tBmw4UZG9TM+yxQr3W9RGyUsg9zzfowVM1fOrSGZVLrYxu5ONBvk8zVCdfyGVhuLXUZUVYNbWOnntva1AiFfN1pijRUpyhk7zV/txS5aewLuVecbZ3dy/X6/yeKRC16kIax7Qk79yHyeNXT8fd08jdQy4E98VQq9Vn/vWo5NGQ/fkAjtPjrS8ifApdhRxBDgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> и имеем .

Пример 2. Исследовать на устойчивость решение вырожденного уравнения для уравнения

Решение. Вырожденное уравнение имеет два решения . Имеем

так что решение устойчивое

так что решение вырожденного уравнения неустойчивое (рис. 51).

Пример 3. Исследовать на устойчивость решение вырожденного уравнения, отвечающего уравнению

Решение. Вырожденное уравнение имеет корень второй кратности. Функция 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAALkAAAAaBAMAAAAZC+AvAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAhEGnwQEQMSFh0HHnUV2ErEoAAAL8SURBVEjH1VXPaxNBFH67m83uugSytARFDaF68BSKEfVQi2LSCoJssSeVssWiHkTiLwQPJUr+gAj1UqUYiz0ED1FKD0VCWq3SiFLQoxaSNiYhxL/BN7ObdHc2iSjm4EBmN29mvn3zve+9B/AfjAeRRA/RF7j3vQOX6nKjh74vdUEX8Xeb8WbQvet4+9NfyMQtdAL3RkdAYlf7XNuEVPvjQhan+3HW/NCKsxApwa4NANWwLRKDcyzqbTkB7yo6OHKNsY+tRE24G9pRmMXnnP37yhp7w9V24L4SQL8Ol43vzMI+w2OSu7kB4jryOuxwbp3Zrj5rhz72A70LQSZKv60+bgVpBZQKfQsmQKqi4a3jXIRM/AAdlCp/O/QL+M1xv6xpdNW7GLDsfBH4Onl59FlLqGXgte39JgX9ga94qTfkJpMaHcQ8gYHwnb4XcYTvZjCdgrEXO7qateA5RN8iL7cKA4YQA/lA7RBdmLqbOfYRIMzkdjgEoF0sJE86hBF8nQCubJPtU1O3XAP4beprEcCDZ85bcTwM5yYbJpoD3cAk4GthRyKIQRQGX7ZbDlJ4rmSh8zWkDtEvWedS4jtv3EJXKTF7iXlOBz7OVSWis1dNq5hB/vgSuOAJMxSdq5jo01lrXS6SeZqgczvomyQOHvN+LXRybxf6qB1dKJvM5JpUKKUmzwwzGFqmQPhIeeErbmZ8RSIbIqoYyjZG5L4HiPYiQllEFYTjrqgqZzZTasopdyXrjOqMGVW8lOnkBEpVwQ1RaVD6mcALXc8raMq5FempDoeSjpTz5JMGcGs2Re623oZAoOkXRiHLmE3fIob3JXqWfj5/CvcdYbLJ4wd1/kl61MnMFv4fb9HlXW5mE0ydHaKXz6GwSSWQ4zooiC7psq67K4GCrlwBtlhdBVoJmtViyZZoxCqfoE7OWOWylUJKnq1iHzpV8OXOXYWrf6JVxPz+nR1GXdW8r1N7WO3SEgtU5lb3CPxN9/B3aYmi+fh954NOnU/8F51Z1P/4yC/Sm7UN4zo0AAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> в окрестности этого корня, и 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAG8AAAAYBAMAAAAGzL4qAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/UGBGsE9XKEx4JGxcdABEMZC1QAAAbxJREFUOMvFlM8rBGEYx7+NEbPosWVahexii1ysJU4aLia1sRuR/BFW9kCUNgdpD1OOCsnmIO3FyYl/QPwLUm4aRY7reWfG7OxYW7sXTz3zPu/zvJ+nZ573B/A/0tJeJxg448+xlWK9JnD6EVBehEXPv4Ky5vfMnDoGpTkWCAMJ0LR/2cf2iM/zdXVoOOYB6zjrk4bmvfJVpN77wYjRcOGY56wh1lUTSoe/sIgFSmOu4wFyj5XTlLk3EgPUyRqqDGJn360B1M1jU7Lb4P9qKECaVEdBK3+AFHVIhcGgCeQ2MmILWhegDIYG7H/FTJ+QIS/IZMoaJRtUnGZ8LgCNBQJinAxHcSETZSBIT5kecDlugxx+F0kssEKpQvSUB8zntR8wsl4dJP21BDYapVJjGqqVCn1ZxGRVNBbDjpObQ0kzC0yJ1BWbM2g3B2+Qu4CT+eKumLUVgCXlDrQmZt5y0w4Yzf44tDbe9BY1afVVnJh0TgP1+I5cMhjsFUZm372E17eiGbNb9oJLrt7A7yNHZtHavRtyy0hsCn/RnlPGdvoPeSmBJ1VZYC5sX02t1ldAWbSyvdb+fvTX8XTUId9rEmFOUsSE2wAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />. Следовательно, решение — полуустойчивое, и если начальная точка лежит в полуплоскости под прямой (область притяжения корня ), то интегральная кривая , выходящая из точки , будет при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> оставаться в окрестности линии (рис.52).

ВОЗМУЩЕНИЙ ТЕОРИЯ

ВОЗМУЩЕНИЙ ТЕОРИЯ — комплекс методов исследования различных задач, используемый во многих разделах математики, механики, физики и техники. Здесь с общей точки зрения излагаются основные идеи В. т.

B. т. основана на возможности приближенного описания исследуемой системы с помощью нек-рой специальным образом выбираемой «идеальной» системы, допускающей корректное и полное изучение. Одним из признаков применимости В. т. в одной из ее форм, определяемой спецификой конкретной задачи, для к-рой В. т. разрабатывается, является условие того, что уравнения, описывающие исследуемый процесс, содержат в явной или неявной форме малый параметр (или несколько таких параметров). При этом требуется, чтобы при нулевом значении малого параметра уравнения допускали точное решение, и таким образом проблема сводится к нахождению асимптотики наилучшего приближения к истинному решению с точностью до ε, ε 2 , . .

1) В. т. впервые была предложена для решения проблем небесной механики, связанных с изучением движения планет в солнечной системе. Удаленность планет друг от друга и малая величина их массы в сравнении с массой Солнца позволяют пренебрегать гравитационным взаимодействием планет между собой и рассматривать их движение (в первом приближении) по орбитам Кеплера, определяемым из уравнений двух тел задачи — планеты и Солнца.

Существенное уточнение астрономич. данных сформулировало проблему учета влияния других планет на движение одной из них вокруг Солнца. Так возникла классическая трех тел задача, причем, напр., при изучении системы Луна — Земля — Солнце в качестве малого параметра выбиралось отношение масс Луны и Земли. Начиная с трудов Ж. Лагранжа (J. Lagrange), П. Лапласа (P. Laplace) было выдвинуто представление о том, что постоянные величины, характеризующие движение планеты вокруг Солнца, ввиду влияния движения других планет как бы «возмущаются» и претерпевают изменения, зависящие от времени; отсюда идет и наименование «теория возмущений».

В. т. занимала внимание классиков Ж. Лагранжа, П. Лапласа, С. Пуассона (S. Poisson), К. Гаусса (С. Gauss) и в результате их работ оказалось возможным проводить вычисления с чрезвычайно большой точностью. Триумфом В. т. явилось открытие планеты Нептун (1848) Дж. Адамсом (J. Adams) и У. Леверье (U. Le Verrier) из анализа отклонений в движении планеты Уран.

Трудности первоначально разработанных методов В. т. были обусловлены наличием в получающихся разложениях членов, содержащих время t вне знака синуса или косинуса. Вклад таких членов в ряд В. т. существен лишь за длительные промежутки времени (порядка столетий), но и в этом случае невозможно строгое описание планетных движений в схеме В. т.- приемлемым является только первое приближение. Появление так наз. секулярных членов обусловлено зависимостью частоты движения (обращения) исследуемой планеты от соответствующих частот других планет. Учет такого рода зависимости и приводит к возникновению в решениях как секулярных (вида At n ), так и смешанных (вида Bt cos (ωt + φ)) членов. Напр., соотношение

в схеме В. т. допускает следующее разложение по ε (ε〈〈1):

смешанный член в к-ром появляется в результате разложения колебания с частотой (1) по колебаниям с частотой ω₀.

Создание специальных методов В. т., устраняющих секулярные члены, т. е. позволяющих представить решение в чисто тригонометрич. виде, связано с работами Линдштедта (Lindstedt), П. Гульдина (P. Guldin), Ш.Делоне (Ch. Delaunay), Б. Волина (В. Bohlin), С. Ньюкома (S. Newcomb). В предложенном ими подходе частоты уже не разлагаются по малым параметрам, т. е. в соответствующие разложения входят не частоты нулевого приближения, а нек-рым образом переопределенные (в терминах современной теоретич. физики — ренормированные) частоты. В результате каждый отдельный член ряда В. т. но Степеням малого параметра представляет собой сходящееся выражение. Вопрос о сходимости ряда В. т. в целом остается открытым из-за появления так наз. малых знаменателей (малых делителей), образующихся при интегрировании в каждом приближении В. т. выражений вида expjω_jn_it + φ>, где <ω_j> — набор частот, отвечающих различным движениям. В случае почти соизмеримых частот сумма в показателе экспоненты может быть малой и тогда после соответствующего интегрирования возникают члены ряда В. т., знаменатели к-рых малы, что и приводит к расходящимся выражениям ряда В. т. В частности, для двух частот ω₁ и ω₂, отношение к-рых является иррациональным числом, (n₁ω₁ + n₂ω₂) можно подобрать так, чтобы соответствующий ряд В. т. расходился.

При изучении с общей математич. точки зрения проблемы малых знаменателей А. Пуанкаре (Н. Poincaré) и А. М. Ляпуновым была предложена методика построения специального вида периодич. решений, эффективная не только в задачах небесной механики, но и в теории дифференциальных уравнений в целом.

Существенный вклад в решение проблемы малых делителей был сделан в работах [4], [5], [6]. Метод последовательных канонич. замен переменных позволяет «понизить» порядок возмущения и с помощью достигаемой усиленной сходимости (так наз. сверхсходимости) «преодолеть» расходимость ряда В. т. из-за малых знаменателей, возникающих в каждом порядке В. т., надлежащим выбором канонич. преобразования.

2) В В. т. для задач небесной механики развито асимптотич. интегрирование дифференциальных уравнений только в случае консервативных систем. Дальнейший прогресс В. т. связан с развитием теории колебаний, в особенности с созданием теории нелинейных колебаний.

Важную роль сыграли (выполненные в развитие работ Ж.Лагранжа) исследования Б. Ван дер Поля (В. Van der Pol) по уравнениям типа Рэлея с малым параметром ε:

Частным случаем уравнения (3) является Ван дер Поля уравнение.

Для решения уравнения

ẍ — ε(1 — ẋ 2 )ẋ + ω 2 х = 0 (4)

в первом приближении Б. Ван дер Поль предложил без должного математич. обоснования метод «медленно меняющихся коэффициентов», аналогичный одному из методов, применявшихся еще Ж. Лагранжем в небесной механике. Этот метод основан на представлении решения уравнения (4) в виде функции гармония, колебаний, амплитуда и фаза к-рых — медленно меняющиеся функции параметра t.

Общая теория нелинейных колебаний была разработана в работах Н. М. Крылова и Н. Н. Боголюбова. При этом были преодолены принципиальные математич. трудности и дано распространение В. т. на общие неконсервативные системы. Развитые в этих работах новые асимптотич. методы нелинейной механики позволяют получать решения в высших приближениях В. т. в математически обоснованной схеме, причем наряду с периодич. решениями допускали строгое рассмотрение квазипериодич. режима.

Идея асимптотич. методов теории возмущений Крылова-Боголюбова становится наглядной при рассмотрении уравнения

описывающего нелинейные колебания системы с одной степенью свободы.

К правильной формулировке асимптотич. метода можно прийти, исходя из физич. соображений о характере колебательного процесса. Так, при полном отсутствии нелинейности, т. е. при ε = 0, колебания, описываемые уравнением (5), будут чисто гармоническими с постоянной амплитудой и равномерно вращающейся фазой. В случае, если ε ≠ 0, т. е. в случае наличия нелинейного возмущения, естественно ожидать появления в решении уравнения (5) обертонов, зависимости мгновенной частоты от амплитуды и, наконец, систематич. увеличения или уменьшения амплитуды колебания в связи с притоком или поглощением энергии возмущающими силами.

Принимая во внимание все эти физич. соображения, естественно решение уравнения (5) искать в виде ряда

х = а cos ψ + εu₁(a, ψ) + ε 2 u₂(a, ψ)+ . (6)

в к-ром u_i(a, ψ), i = 1, 2, . — периодич. функции угла ψ с периодом 2π, а величины а и ψ как функции времени определяются дифференциальными уравнениями

Таким образом, задача сводится к подбору соответствующих выражений для функций u_i(a, ψ), A_i(а), В_i(а), i = 1, 2, . так, чтобы выражение (6), в к-рое вместо а и ψ будут подставлены функции времени, определенные из системы (7), являлось решением исходного уравнения (5). Причем накладываются нек-рые дополнительные условия, обеспечивающие отсутствие в решении (6) секулярных членов.

Ограничиваясь в формальном ряде (6) первыми членами, приходят к m-му приближению, обладающему свойством асимптотичности в том смысле, что при фиксированном m и ε → 0 выражение (6) стремится к точному решению уравнения (5); уравнения первого приближения совпадают с уравнениями Ван дер Поля. Проблема оценки погрешности m-го приближения не вызывает особенных трудностей. Аналогичным образом решается задача в случае N степеней свободы.

Если интерпретировать формулу (6) не как решение уравнения (5), а как формулу замены переменных, то можно получить точные выражения для производных по времени от амплитуды а и фазы ψ.

Как известно (см. [8], [9]) во многих случаях дифференциальные уравнения, описывающие колебательные процессы и содержащие «малый» параметр, могут быть приведены к так наз. стандартной форме:

где ε — малый положительный параметр. Большое число задач физики и техники приводится к этому виду. Для системы дифференциальных уравнений вида (8) разработан особый метод аппроксимации, названный методом усреднения. Согласно методу усреднений, эти уравнения для достаточно малых значений ε на конечном интервале посредством замены переменных

приводятся к усредненным уравнениям:

Применяя метод усреднения, можно получить, напр., ряд критериев о существовании и устойчивости автоколебательных режимов.

Были установлены [13] при весьма общих условиях оценки разности |X_i — ε_i| на временном интервале длины L/ε. Кроме того, можно установить соответствие и в таких свойствах решений общих систем, к-рые зависят от их поведения на бесконечном интервале. Таким образом были доказаны теоремы о существовании и устойчивости квазипериоднч. решений.

3) При изучении нелинейных колебательных систем можно не приводить соответствующую систему уравнений к «стандартной форме», а работать непосредственно с исходными дифференциальными уравнениями для системы гармонич. вибраторов, подверженных слабому нелинейному воздействию. При этом наряду с общими решениями для такой системы можно получить и частные решения с помощью замены переменных специального вида.

Такой подход был использован Н. Н. Боголюбовым для нек-рых задач статистич. механики, связанных с вычислением функций распределения s частиц (s = 1, 2, . N) для систем многих взаимодействующих частиц. Малым параметром в задачах статистич. механики может служить как малая константа взаимодействия, так и малая плотность частиц в системе. В одном из этих приближений можно выразить высшие s-частичные функции распределения через функции распределения одной частицы. При этом уже в первом приближении В. т. можно получить из системы кинетич. уравнений известные уравнения Больцмана, а также уравнения Ландау, Власова и Боголюбова-Ленарда-Балеску, широко применяемые в теории плазмы.

Следует отметить, что перечисленные методы развиты в применении к уравнениям с малым параметром, входящим в них регулярным образом (не при старшей производной). В то же время, напр., уравнение Ван дер Поля в форме Рэлея в случае больших ε автоматически сводится к уравнению, в к-ром малый параметр стоит перед старшей производной. Для задач такого типа, требующих особого подхода, развиты мощные методы исследования (см. [14], [15], [16], [17]).

Именно задачи с малым параметром при старшей производной типичны для проблем статистич. механики и гидродинамики. Примером может служить Навье-Стокса уравнение в предположении малых коэффициентов вязкости и теплопроводности, имеющее в качестве нулевого приближения уравнения идеальной жидкости Эйлера. Поиск наилучшего приближения в данной задаче усложнен указанным условием.

4) Большое значение методы В. т. имеют в области квантовой механики, где, такие как и в классической, точные решения получены лишь в задаче двух тел, формально сводимой к задаче одного тела во внешнем потенциальном поле. Здесь используются две формы В. т.: одна для стационарных состояний, другая для расчета вероятностей переходов из одного стационарного состояния в другое в схеме метода матрицы рассеяния. В. т. формулируется в квантовой механике как задача на собственные значения для линейного самосопряженного оператора вида:

где ε — малый параметр, причем известно решение задачи на собственные значения для «невозмущенного» оператора H₀, т. е. задана полная система собственных функций <ψ (0) _n> и собственных значений Е 0 _n и требуется найти спектр оператора Н.

В предположении малости ε волновые функции

и собственные значения энергии Е_n могут быть найдены в виде рядов

по степеням возмущения ε. Тогда для возмущения n-состояния В. т. дает следующий результат:

Здесь V_mn — матричный элемент оператора возмущения, определяемый согласно правилу (V̂ = εH₁):

где dq — элемент объема. Условие применимости В. т. к таким задачам:

нарушается в случае вырождения уровня энергии невозмущенной системы: вырожденному уровню энергии Е (0) _n отвечает s состояний <ψ (0) _nj>, j = 1, 2, . s (s — кратность вырождения). В этом случае применяется нек-рая модификация В. т.: вначале учитывают влияние возмущения на вырожденные состояния, а влияние других уровней рассматривается как малое возмущение; строятся линейные комбинации s функций вырожденного состояния, причем для коэффициентов С (0) _r построенной комбинации получены уравнения вида

Поправка к энергии Е (1) _n находится из секулярного уравнения системы (9). Решения <Е (1) _n,p>, p = 1, . s этого уравнения s-й степени представляют в (9) и находят <С (0) _r,p> и волновую функцию:

после снятия вырождения. Поправки следующего порядка находят методами обычной В. т.

В нестационарном случае задача В. т. ставится в терминах вероятностей перехода из состояния ψ (0) _n в состояние &#968 (0) _m. В. т. может применяться в гейзенберговском, шрёдингеровском представлениях или же в представлении взаимодействия.

В квантовой механике есть также принципиально другого типа задачи о нахождении так наз. рассеяния матрицы двух или нескольких частиц. В особенности такие задачи важны для квантовой электродинамики, где имеется малый параметр — постоянная тонкой структуры.

Проблема вычисления вероятностей перехода сводится к исследованию гамильтониана вида:

где Н₀ — свободный гамильтониан, а Н₁ — гамильтониан взаимодействия, к-рый по предположению включается в «отдаленном прошлом» (t = -∞) и выключается в «отдаленном будущем» (t = +∞).

В представлении взаимодействия Шрёдингера уравнение имеет вид:

Посредством замены переменных

можно получить для состояния φ уравнение

Связь между начальными состояниями φ_in, описывающими «входящие» частицы, и конечными состояниями φ_out описывающими «выходящие» частицы, формулируется в терминах так наз. оператора рассеяния S, определяемого соотношением вида:

Формально решение уравнения (10) можно построить методом последовательных приближений в виде разложения по степеням малости взаимодействия:

В квантовой теории поля справедлива аналогичная формула, в к-рую вместо H₁(t) входит соответствующая плотность лагранжиана, причем используется представление S-оператора через T-произведение:

Действие оператора хронологического упорядочения т определяется правилами:

причем это T-произведение формально не определено для совпадающих аргументов. Для преодоления такого рода трудностей, возникающих в методе В. т. в квантовой теории поля, созданы специальные методы регуляризации. Релятивистски инвариантная В. т. используется для вычисления так наз. S-матрицы, элементы к-рой определяют вероятности переходов между квантовыми состояниями различных полей под влиянием взаимодействия между ними.

Лит.: [1] Роinсаré Н., Les méthodes nouvelles de la mécanique céleste, P., t. 1-3, 1892-97; Пуанкаре A., Избр. труды, т. 1-3, M., 1971 — 74; [2] Шарлье К., Небесная механика, пер. с нем., М., 1966; [3] Биркгоф Дж. Д., Динамические системы, пер. с англ., М.-Л., 1941; [4] Колмогоров А. Н., О динамических системах с интегральным инвариантом на торе, «Докл. АН СССР», 1953, т. 93, № 5; [5] Арнольд В. И., Математические методы классической механики, М., 1974; [6] Мозер Ю., Лекции о гамильтоновых системах, пер. с англ., М., 1973; [7] Боголюбов Н. Н., Крылов Н. М., в кн.: Збiрник праць з нелiнiйноï механiки, К., 1937, с. 55-112; [8] их же, Введение в нелинейную механику, К., 1937; [9] Боголюбов Н. Н., Mитропольский Ю. А., Асимптотические методы в теории нелинейных колебаний, 5 изд., М., 1974; [10] Моисеев Н. Н., Асимптотические методы нелинейной механики, М., 1969; [11] Челомей В. Н., «Докл. АН СССР», 1956, т. 110, №3; [12] Боголюбов Н. Н., Митропольский Ю. А., Самойленко А. М., Метод ускоренной сходимости в нелинейной механике, К., 1969; [13] Боголюбов Н. Н., О некоторых статистических методах в математической физике, К., 1945; [14] Дородницын А. А. «Прикл. матем. и мех.», 1947, т. 11; [15] Тихонов А. Н., «Матем. сб.», 1948, т. 22, с. 193-204; [16] Понтрягин Л. С., «Изв. АН СССР. Сер. матем.», 1957, т. 21, с. 607; [17] Мищенко Е. Ф., «Изв. АН СССР. Сер. матем.», 1957, т. 21, с 607; «Изв. АН СССР. Сер. матем.», 1957, т. 21, с. 627; [18] Блохинцев Д. И., Основы квантовой механики, 5 изд., М., 1976; [19] Боголюбов Н. Н., Лекцiï з квантовоï статистики, К., 1949; [20] его же, Избранные труды, т. 2, К., 1970; [21] БоголюбовН. Н., Ширков Д. В., Введение в теорию квантованных полей, 3 изд., М., 1976; [22] Боголюбов Н. Н., Логунов А. А., Тодоров И. Т., Основы аксиоматического подхода в квантовой теории поля, М., 1969; [23] Ахиезер А. И., Берестецкий В. Б., Квантовая электродинамика, 3 изд., М., 1969; [24] Маслов В. П., Теория возмущений и асимптотические методы, М., 1965.

Н. Н. Боголюбов (мл.).

1. Математическая Энциклопедия. Т. 1 (А — Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] — М., «Советская Энциклопедия», 1977, 1152 стб. с илл.

Метод возмущений дифференциальные уравнения с малым параметром

Метод возмущений: алгебраические уравнения (СОБОЛЕВ В.А. , 1999), МАТЕМАТИКА

Описаны первоначальные сведения из теории возмущений применительно к задаче нахождения корней многочленов. Метод возмущений, основанный на разложении по малому параметру, позволяет вслед за решением невозмущенной задачи, соответствующей нулевому значению малого параметра, находить приближенное решение исходной возмущенной задачи.

МЕТОД ВОЗМУЩЕНИЙ: АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ

Самарский государственный университет

Теория возмущений впервые возникла в рамках одной из старейших областей прикладной математики — небесной механике. Начиная с античных времен для описания движения планет применялись различные математические методы. После открытия закона всемирного тяготения оказалось возможным описывать планетарные движения на основе фундаментальных физических законов. Если рассматриваются только Солнце и одна планета, то она движется по эллипсу, в фокусе которого находится Солнце. Однако реально наблюдается несколько иное движение. Дело в том, что каждая планета оказывает воздействие на другие своим гравитационным полем и поэтому возмущает, то есть изменяет, их движение. Теория возмущений в ее изначальном смысле связана с разработкой различных способов учета таких изменений. Исследователь берет в основу анализа невозмущенное решение, которое соответствует эллиптическому движению как начальное приближение, и затем соответствующим образом корректирует это решение, вычисляя силы, с которыми планеты влияют на невозмущенное движение друг друга.

В настоящее время задачи, стоящие перед теорией возмущений, гораздо шире, чем ее применения в небесной механике, но основная идея сохранилась. Исследование начинается с невозмущенной или порождающей задачи, решение которой рассматривается как приближение более сложной задачи, отличающейся наличием дополнительных малых членов в уравнениях. Затем строятся следующие приближения, уточняющие это решение, обычно в форме степенных рядов (или их модификаций). Роль переменной в таких степенных рядах играет малая величина, называемая малым параметром. Обычно используются только частичные суммы рядов (в большинстве задач два-три слагаемых).

Простейшая задача, в которой можно применить теорию возмущений, — это задача о вычислении корней многочленов. Эта задача позволяет проиллюстрировать многие важные идеи: описание семейства возмущений, вырожденные и невырожденные случаи, равномерные и неравномерные решения, масштабирование координат и параметров. Задачу будем рассматривать как чисто математическую, мы не будем обращаться к физическим источникам каждой задачи, а будем обсуждать чисто математические трудности, порождаемые природой теории возмущений. При таком подходе полиномиальные уравнения представляют собой идеальный объект для изучения.

Применение метода возмущений для нахождения корней многочлена продемонстрируем на квадратном уравнении

x2 — 3,99x + 3,02 = 0.

Конечно, это уравнение нетрудно решить точно. Тем не менее мы опишем подход, основанный на методе возмущений, в соответствии с которым следует выполнить программу действий, состоящую из следующих четырех шагов.

1. Во-первых, заметим, что, поскольку — 3,99 = = — 4 + 0,01 и 3,02 = 3 + 0,02, уравнение (1) — это почти то же, что уравнение x2 — 4x + 3 = 0 или (x — — 1)(x — 3) = 0, корнями которого являются числа x(1) = 1, x(2) = 3.

2. На втором шаге создается семейство задач, связывающее легко решаемое уравнение с уже известными корнями и первоначальное уравнение (1). Это можно сделать обозначив через e малую величину 0,01, так что — 3,99 = — 4 + e; 3,02 = 3 + 2e. Тогда уравнение (1) можно переписать следующим образом:

x2 + (e — 4)x + (3 + 2e) = 0.

Если теперь позволить e изменяться, то одно уравнение (2) превратится в семейство уравнений, причем каждому значению e соответствует одно уравнение. Если e = 0, то (2) сводится к уже решенному уравнению; если e = 0,01, то имеем исходное уравнение (1). Уравнение (2) дает пример семейства возмущений, то есть семейства задач, зависящих от малого параметра e, легко решаемых при e = 0.

3. Третий шаг состоит в нахождении приближенных решений семейства уравнений (2) в виде многочленов (усеченных степенных рядов), роль переменной в которых играет малый параметр e. Метод нахождения будет описан в следующем разделе. Для рассматриваемого примера вполне подходящими будут приближенные решения

Полагая в этих формулах e = 0,01, получим приближенные решения исходного уравнения (1):

x(1) . 1,015 875, x(2) . 2,974 812 5.

4. На четвертом шаге следует, насколько это возможно, оценить ошибку полученного приближения. Этим вопросом мы не будем заниматься в данной статье.

Даже этот простой пример дает хорошее представление о теории возмущений. Прежде всего метод может применяться только тогда, когда исходная задача близка к легко решаемой задаче (к задаче, решение которой известно точно или может быть найдено приближенно каким-то методом, не связанным с теорией возмущений). Произвольно выбранное алгебраическое уравнение не всегда может быть решено методом возмущений, так как оно необязательно окажется близким к уравнению с легко определяемыми корнями. Кроме того, этот пример показывает, что применение метода возмущений дает не только решение исходной задачи (1), но и каждого уравнения семейства (2), если только величина e достаточно мала. Возмущенное решение типа (3) справедливо в том смысле, что дает хорошее приближение только для достаточно малых значений e. Что означают слова «достаточно малое», неясно до тех пор, пока не сделан четвертый шаг (анализ ошибки приближения). Может оказаться, что e = 0,01 недостаточно мало, чтобы дать хорошее решение нашей задачи. Тогда мы не можем решить исходную задачу, но в то же время можем получить хорошее решение задачи (2) для меньших значений малого параметра, например при e = = 0,001. Кроме того, формулы (3) могут давать приемлемое решение при e = 0,1 и даже для значений параметра, равных 1 или 10. Здесь мы столкнулись с отличием природы семейств возмущений от индивидуальных задач. Обычно считается, что в теории возмущений 0 0. Построить приближенное решение методом, изложенным в предыдущем разделе, невозможно, так как в данном примере мы имеем дело с вырожденным случаем: x0 = 0 и jx(x0 , 0) = 0. В математической литературе для рассмотрения вырожденных случаев обычно рекомендуется использовать метод диаграмм Ньютона [2], однако в прикладных работах широко используется более простой эвристический метод, не имеющий общепринятого названия, но иногда называемый методом неопределенных масштабов. Суть метода заключается в том, что приближенное решение ищется в форме

x . x0d0(e) + x1d1(e) + _ + xkdk(e)

вместо менее общей полиномиальной формы x . . x0 + x1e + _ + xkek. Функции dn(e) определяют последовательно вместе с коэффициентами xn . Этот метод в комбинации с другими методами важен для сложных задач, которые возникают, например, в газовой динамике, когда невозможно заранее предугадать вид этих функций. Мы продемонстрируем применение этого метода для приближенного нахождения корней многочленов в вырожденном случае. Рассмотрим вырожденную задачу x2 — 10x + + 25 — 4e — 4e2 = 0, имеющую точные решения Эти решения нельзя разложить в степенные ряды по e, но можно разложить в степенные ряды по Например, 5 + 2e1/2 + e3/2 + _ Последняя формула имеет вид (13) при x0 = 5, d0 = 1, x1 = 2, d1 = = e1/2 и т.д. Предугадать вид функций dn(e), основываясь на виде уравнения, не представляется возможным даже в этом простом случае. В общей ситуации заранее можно предполагать только то, что функции dn(e) располагаются в порядке важности. Другими словами, приближение наименьшего порядка должно задаваться формулой x . x0d0(e); член x1d1(e) должен играть роль меньшей (по абсолютной величине) поправки; x2d2(e) — еще меньше и т.д., по меньшей мере при достаточно малых значениях e. Точнее, для всех n должно выполняться предельное соотношение dn + 1(e) / dn(e) 0, когда e 0.

Рассмотрим еще один пример:

Невозмущенное уравнение имеет трехкратный корень x = 1. Полагая x . 1 + x1d1 в исходном уравнении, получим . 0. Отсюда находим d1 = e1/2, а для x1 получается уравнение имеющее один вещественный корень x1 = -1. В результате получаем следующее приближенное решение:

Дополнительные сведения и большое количество примеров можно найти в прекрасно написанных книгах [3, 4]. Материалы книги [4] существенно использовались при написании настоящей статьи.

1. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. М.: Изд-во МГУ, 1985. Т. 1.

2. Вайнберг М.М., Треногин В.А. Теория ветвления решений нелинейных уравнений. М.: Наука, 1969.

3. Найфэ А.Х. Введение в методы возмущений. М.: Мир, 1984.

4. Murdock J.A. Perturbations: Theory and Methods. N.Y.: Wiley, 1991.

Владимир Андреевич Соболев, доктор физико-математических наук, профессор, академик РАЕН, зав. кафедрой дифференциальных уравнений и теории управления Самарского государственного университета, декан факультета математики и компьютерных наук Самарского муниципального университета Наяновой. Область научных интересов — дифференциальные уравнения, теоретическая механика, математическое моделирование, теория управления. Автор более 80 научных публикаций и четырех книг.