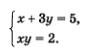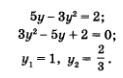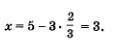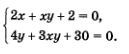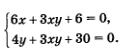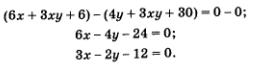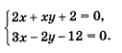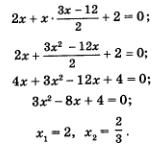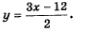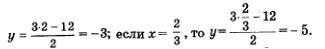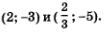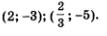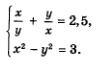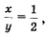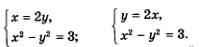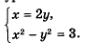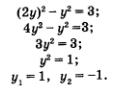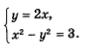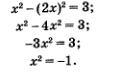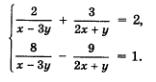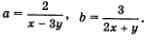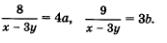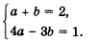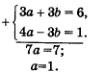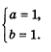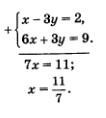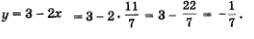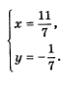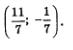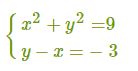Метод введения переменной при решении систем уравнений

Конспект урока «Решение систем уравнений методом введения новой переменной»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Открытый урок по теме

«Решение систем уравнений второй степени методом замены переменной»

1) Открыть совместно с учащимися новый метод решения систем уравнений (метод введения новых переменных), закрепить навыки решения систем уравнений другими методами (графическим, подстановкой и сложением).

2) Формировать потребность приобретения новых знаний, создать условия для контроля (самоконтроля) усвоения умений и навыков.

3) Развивать математическую речь при комментировании решения.

4) Воспитывать уважение друг к другу, взаимопонимание, уверенность в себе, развивать самостоятельность и творчество.

Оптимально использовать методы обучения, соответствующие возрасту и развитию учащихся, для формирования знаний по изучаемой на уроке теме.

1.Создать условия для развития познавательной деятельности учащихся.

2.Способствовать формированию умений переносить знания в новую ситуацию.

3.Развивать математический кругозор, мышление и речь, внимание и память.

Содействовать воспитанию интереса к математике, формировать у учащихся умение осмысленно, целенаправленно организовывать на уроке свою деятельность, осознавать значимость каждого шага для себя.

Воспитывать ответственность за грамотно сформулированные и лаконичные ответы.

Тип урока : комбинированный.

Оборудование : мультимедийный проектор, карточки с заданиями, доска.

1. Организационный этап.

Учитель приветствует учеников.

Знакомит учеников с оценочным листом.

Ученики выставляют себе оценки за организационный этап.

2. Актуализация знаний.

Проверим домашнее задание.

Решить систему уравнений тремя различными методами (графическим, подстановкой и сложением)

Для каждого метода записать алгоритм его использования в тетрадь.

1 метод -графический

1)

Графиком этой функции является парабола, «ветви» направлены вверх, вершина в точке (0;-4)

2)

Графиком этой функции является прямая.

Точки пересечения (1;-3);(-3;5).

Алгоритм использования графического метода:

1.Построить графики уравнений в одной системе координат.

2. Найти координаты точки пересечения или указать, что таких точек нет.

3. Записать ответ.

Из второго уравнения выражаем у:

.

Подставляем в первое уравнение:

Если , то

Если , то

Алгоритм использования метода подстановки:

1. Выразить из какого-нибудь уравнения системы одну переменную через другую.

2. Подставить в другое уравнение системы вместо этой переменной равное ему выражение.

3. Решить получившееся уравнение с одной переменной.

4. Найти соответствующее значение второй переменной

5. Записать ответ.

3 метод- алгебраическое сложение

Сложим уравнения системы, получим:

Если , то

Если , то

Алгоритм использования метода алгебраического сложения:

1. Уравнять модули коэффициентов при какой-нибудь переменной.

2. Сложить или вычесть почленно левые и правые части уравнений системы.

3. Решить получившееся уравнение с одной переменной.

4. Найти соответствующее значение второй переменной

5. Записать ответ.

Какой из способов решения системы вам понравился больше?

Ученики ставят себе баллы в оценочный лист.

3. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Решим систему уравнений:

Какие основные методы решения систем уравнений вы знаете? (графический, подстановкой и сложением)

Какой из этих методов можно было бы применить к этой системе?

Обсуждаем применение графического способа.

Обсуждаем применение способа сложения.

Обсуждаем применение способа подстановки.

Приходим к выводу, что ни один из ранее изученных методов не подходит. Как тогда поступить? Как решать такие системы? Нужен другой метод.

Какую цель мы можем поставить перед собой на сегодняшнем уроке? (изучить другие методы решения систем уравнений второй степени научиться их применять на практике)

4. Первичное усвоение новых знаний .

Итак, решим систему:

Где мы можем узнать, как решаются такие системы? (в учебнике, в интернете).

Далее реализуется способ достижения информации.

Учитель предлагает ученикам выбрать для себя источник информации и воспользоваться им.

Учащихся предлагают ввести новую переменную.

Введём новую переменную .

Тогда первое уравнение системы можно переписать в виде

Умножим обе части уравнения на ( так как по условию ).

;; .

Делаем обратную замену.

Если , то .

Подставляя во второе уравнение системы, получаем: .

это уравнение корней не имеет.

Если , то .

Подставляя во второе уравнение системы, получаем: .

Если , то .

Если , то .

Решим ещё одну систему:

Учащиеся делают вывод, что для решения этой системы одной переменной недостаточно, надо вводить две переменные, например:

.

Если .

Если .

Давайте уточним цель нашего урока (научиться решать системы уравнений второй степени с помощью метода введения новых переменных).

5. Первичная проверка понимания .

Составление алгоритма использования метода введения новых переменных.

Учащиеся разбиваются на пары и вместе со своими соседями по парте составляют алгоритм использования метода введения новых переменных.

Различные варианты ответов зачитываются с места.

Алгоритм использования метода введения новых переменных:

1. Ввести одну или две новые переменные.

2. Записать новое уравнение или систему уравнений.

3. Решить новое уравнение или систему уравнений и найти значения введённых переменных.

4. Сделать обратную замену и найти значения переменных из условия.

5. Записать ответ.

Ученики ставят себе баллы в оценочный лист.

6. Первичное закрепление

Чтобы помочь затрудняющимся ученикам, даётся подсказка:

Сделаем замену переменной:

Получим новую систему:

3. Если , то . Если , то .

4. Получаем две системы:

или

Потом на экране выводится правильное решение.

Сделаем замену переменной . Получим новую систему:

.

Если , то .

Если , то .

Получаем две системы:

или

корней нет

Если , то .

Если , то .

Ученики ставят себе баллы в оценочный лист.

7. Информация о домашнем задании, инструктаж по его выполнению

Найти в Интернете три системы уравнений, которые можно решить методом введения новой переменной.

Записать в тетрадь их условие и решение.

Самые интересные системы будут разобраны на следующем уроке у доски.

8. Рефлексия (подведение итогов занятия)

Давайте заполним оценочные листы и посмотрим, какие у вас получились оценки.

Чему мы научились на сегодняшнем уроке?

(Решать системы уравнений способом замены переменной)

Что необходимо сделать, для того чтобы решить систему уравнений таким способом?

(сделать замену переменной, решить новое уравнение, выполнить обратную замену)

Что было наиболее сложным (трудным)?

Какие вопросы остались после проведения занятия?

Метод введения переменной при решении систем уравнений

В этом параграфе мы обсудим три метода решения систем уравнений, более надежные, чем графический метод, который рассмотрели в предыдущем параграфе.

Метод подстановки

Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим алгоритмом мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4).

Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.

1. Выразить у через х из одного уравнения системы.
2. Подставить полученное выражение вместо у в другое уравнение системы.
3. Решить полученное уравнение относительно х.
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.
5. Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.

Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой.

Пример 1. Решить систему уравнений

1) Выразим х через у из первого уравнения системы: х = 5 — 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 — 3у) у — 2.
3)Решим полученное уравнение:

4) Подставим поочередно каждое из найденных значений у в формулу х = 5 — Зу. Если 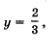то
5) Пары (2; 1) и 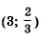решения заданной системы уравнений.

Ответ: (2; 1);

Метод алгебраического сложения

Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере.

Пример 2. Решить систему уравнений

Решение.

Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:
Вычтем второе уравнение системы из ее первого уравнения:

В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:

Эту систему можно решить методом подстановки. Из второго уравнения находим 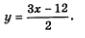Подставив это выражение вместо у в первое уравнение системы, получим

Осталось подставить найденные значения х в формулу

Таким образом, мы нашли два решения системы:

Ответ:

Метод введения новых переменных

С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах.

Пример 3. Решить систему уравнений

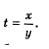
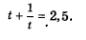
Решение. Введем новую переменную Тогда первое уравнение системы можно будет переписать в более простом виде: Решим это уравнение относительно переменной t:

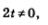
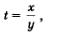
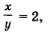
Оба эти значения удовлетворяют условию , а потому являются корнями рационального уравнения с переменной t. Но значит, либо откуда находим, что х = 2у, либо
Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения:

Что же дальше? А дальше каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х 2 — у 2 = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений:

Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений:

Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2у вместо х во второе уравнение системы. Получим

Так как х = 2у, то находим соответственно х₁ = 2, х₂ = 2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1). Решим вторую систему уравнений:

Снова воспользуемся методом подстановки: подставим выражение 2х вместо у во второе уравнение системы. Получим

Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы.

Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном уравнении системы. Именно так обстояло дело в примере 3.Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4.

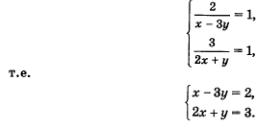
Пример 4. Решить систему уравнений

Введем две новые переменные:

Учтем, что тогда

Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и b:

Применим для решения этой системы метод алгебраического сложения:

Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и b мы получили одно решение:

Возвращаясь к переменным х и у, получаем систему уравнений

Применим для решения этой системы метод алгебраического сложения:

Так как 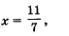то из уравнения 2x + y = 3 находим:
Таким образом, относительно переменных х и у мы получили одно решение:

Ответ:
Завершим этот параграф кратким, но достаточно серьезным теоретическим разговором. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что основная идея решения уравнения состоит в постепенном переходе от одного уравнения к другому, более простому, но равносильному заданному. В предыдущем параграфе мы ввели понятие равносильности для уравнений с двумя переменными. Используют это понятие и для систем уравнений.

Две системы уравнений с переменными х и у называют равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.

Все три метода (подстановки, алгебраического сложения и введения новых переменных), которые мы обсудили в этом параграфе, абсолютно корректны с точки зрения равносильности. Иными словами, используя эти методы, мы заменяем одну систему уравнений другой, более простой, но равносильной первоначальной системе.

Графический метод решения систем уравнений

Мы уже с вами научились решать системы уравнений такими распространенными и надежными способами, как метод подстановки, алгебраического сложения и введения новых переменных. А теперь давайте с вами вспомним, метод, который вы уже изучали на предыдущем уроке. То есть давайте повторим, что вы знаете о графическом методе решения.

Метод решения систем уравнения графическим способом представляет собой построение графика для каждого из конкретных уравнений, которые входят в данную систему и находятся в одной координатной плоскости, а также где требуется найти пересечения точек этих графиков. Для решения данной системы уравнений являются координаты этой точки (x; y).

Следует вспомнить, что для графической системы уравнений свойственно иметь либо одно единственное верное решение, либо бесконечное множество решений, либо же не иметь решений вообще.

А теперь на каждом из этих решений остановимся подробнее. И так, система уравнений может иметь единственное решение в случае, если прямые, которые являются графиками уравнений системы, пересекаются. Если же эти прямые параллельны, то такая система уравнений абсолютно не имеет решений. В случае же совпадения прямых графиков уравнений системы, то тогда такая система позволяет найти множество решений.

Ну а теперь давайте с вами рассмотрим алгоритм решения системы двух уравнений с 2-мя неизвестными графическим методом:

• Во-первых, вначале мы с вами строим график 1-го уравнения;
• Вторым этапом будет построение графика, который относится ко второму уравнению;
• В-третьих, нам необходимо найти точки пересечения графиков.
• И в итоге мы получаем координаты каждой точки пересечения, которые и будут решением системы уравнений.

Давайте этот метод рассмотрим более подробно на примере. Нам дана система уравнений, которую необходимо решить:

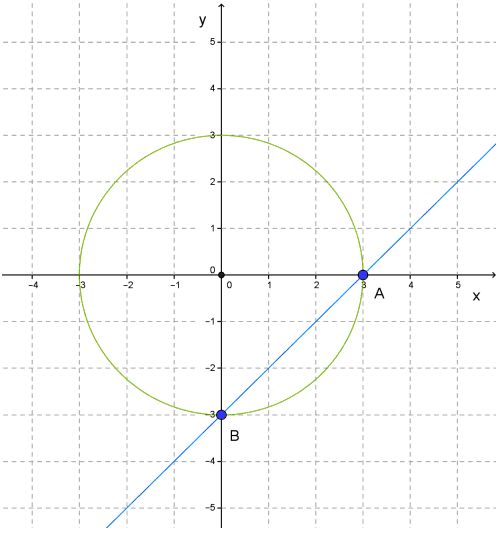
1. Вначале мы с вами будем строить график данного уравнения: x2+y2=9.

Но следует заметить, что данным графиком уравнений будет окружность, имеющая центр в начале координат, а ее радиус будет равен трем.

2. Следующим нашим шагом будет построение графика такого уравнения, как: y = x – 3.

В этом случае, мы должны построить прямую и найти точки (0;−3) и (3;0).

3. Смотрим, что у нас получилось. Мы видим, что прямая пересекает окружность в двух ее точках A и B.

Теперь мы с вами ищем координаты этих точек. Мы видим, что координаты (3;0) соответствуют точке А, а координаты (0;−3) соответственно точке В.

И что мы получаем в итоге?

Получившиеся при пересечении прямой с окружностью числа (3;0) и (0;−3), как раз и являются решениями обоих уравнений системы. А из этого следует, что данные числа являются и решениями этой системы уравнений.

То есть, ответом этого решения являются числа: (3;0) и (0;−3).

Метод введения новых переменных

Метод введения новых переменных

учитель школы «Логос ЛВ», ст. преп. фак-та довузовской подготовки МИТХТ, г. Москва

Тема: Системы уравнений

Урок: Метод введения новых переменных

1. Тема урока, введение

На предыдущих уроках для решения систем уравнений применялись графический метод, метод подстановки и метод алгебраического сложения. Сейчас будет рассмотрен метод введения новых переменных.

2. Пример на введение новых переменных

Введение новых переменных позволяет упростить исходную систему. Рассмотрим в качестве примера систему, которая предлагалась на вступительном экзамене в 1979 г. в МГУ на механико-математический факультет.

Пример 1. Решить систему

Полезно ввести новые переменные

Довольно сложная исходная система свелась к более простой. Это система двух линейных уравнений относительно a и b. Решим ее методом алгебраического сложения, вычтем из первого уравнения второе.

Мы ввели новые переменные и решили систему относительно этих переменных. Возвращаемся к старым переменным.

Мы получили вторую систему двух линейных уравнений относительно x и y.

Решим систему методом подстановки.

Ответ:

3. Основные сведения о квадратных уравнениях

Часто при замене переменных мы получаем квадратное уравнение. Напомним основные сведения о них:

Квадратное уравнение в общем виде:

Формула корней квадратного уравнения через дискриминант:

Если b – четное число, имеем формулу:

Напомним теорему Виета: Если корни квадратного уравнения , то

Верно и обратное: Если числа удовлетворяют системе , то они являются корнями квадратного уравнения .

Напомним прием, который позволяет упростить нахождение корней квадратного уравнения. Умножим квадратное уравнение на Получим

Получили новое уравнение относительно новой переменной

Мы получили приведенное квадратное уравнение с целыми коэффициентами (если они были целыми в исходном уравнении).

4. Примеры приведенных квадратных уравнений с заменой переменных

Пример 2. Решить уравнение

;

Это приведенное уравнение, коэффициенты – целые числа.

По теореме Виета

Ответ:

Пример 3. Решить уравнение

Получили приведенное квадратное уравнение относительно z.

По теореме Виета

Ответ:

Мы рассмотрели еще один прием, который позволяет упростить нахождение корней квадратного уравнения.

5. Решение систем уравнений

После сделанных напоминаний для квадратных уравнений решим систему:

Пример 4. Решить систему

Решение: Произведем замену:

Вернемся к исходной системе:

Ответ:

Пример 5. Решить систему:

Введем новую переменную: Получаем квадратное уравнение относительно новой переменной.

Исходная система свелась к совокупности двух систем:

Каждую систему решаем методом подстановки.

1.

2.

Находим y при известных x.

Ответ:

6. Пример симметрической системы

Следующая система – симметрическая. Симметрической называется такая система, которая не изменится, если переменные поменять местами.

Решение: Произведем замену

Мы ввели новые переменные, и нашли их.

Вернемся к старым переменным. Получаем две системы:

1.

2.

нет решений.

Ответ:

Заметим, что решением симметрической системы являются симметричные пары чисел.

Мы рассмотрели метод введения новых переменных. На следующем уроке рассмотрим системы повышенной сложности.

Список рекомендованной литературы

1. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / , и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев . 9 класс : учеб. для учащихся общеобразоват. учреждений / , , . — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. , , Сидоров . 9 класс. 16-е изд. — М., 20с.

5. Мордкович . 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / , . — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / , , и др.; Под ред. . — 12-е изд., испр. — М.: 2010.-223 с.: ил.

Рекомендованные ссылки на интернет-ресурсы

1. Раздел ***** по математике (Источник).

2. Интернет-проект «Задачи» (Источник).

3. Образовательный портал «РЕШУ ЕГЭ» (Источник).

Рекомендованное домашнее задание

1. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / , и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 000, 129.