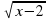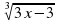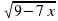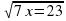Мастер-класс «Методические особенности обучения решению уравнений в курсе математики 5-7 классов»
методическая разработка по алгебре (5 класс) на тему
Прадлагаю вашему вниманию мастер-класс с презентацией
Скачать:
| Вложение | Размер |
|---|---|
| master_klass.docx | 45.21 КБ |
| master-klass.rar | 2.43 МБ |
Предварительный просмотр:
Муниципальное общеобразоательное учреждение
«Гимназия №7» города Подольск Московской области
обучения учащихся решению уравнений
в курсе математики 5-7 классов»
Подготовила и провела
Ялунина Светлана Станиславовна
Мастер класс «Методические особенности обучения учащихся решению уравнений в курсе математики 5-7 классов»
Уважаемые коллеги! Я рада приветствовать вас на мастер-классе «Методические особенности обучения учащихся решению уравнений в курсе математики 5-7 классов».
Цели сегодняшнего мероприятия:
- рассмотреть различные виды уравнений, изучаемые в курсе математики 5-7 классов;
- привести алгоритмы их решения;
- дать методические рекомендации по обучению учащихся решению уравнений.
Я попрошу сегодня вас всех активно принимать участие в работе нашего мероприятия, выступать в роли учеников, не бояться задавать вопросы. Может даже ошибаться. Плохих отметок сегодня не будет.
Эпиграфом нашего мастер-класса я взяла слова современного польского математика Станислава Коваля:
Уравнение – это золотой ключ,
открывающий все математические сезамы.
З накомство ребенка с уравнениями начинается почти с самого начала изучения математики, задолго до ЕГЭ. Еще в младшей школе решаются простейшие алгебраические уравнения, которые служат фундаментом для построения алгоритмов решения уравнений в 11 классе. Каких только разновидностей уравнений не встретишь в школе: алгебраические, иррациональные, тригонометрические, показательные, логарифмические. Голова идет кругом. При этом почти к каждому разделу учебника математики прикрепляются уравнения определенного вида с различной комбинацией изученных действий, функций и разным уровнем сложности. Но важно помнить о том, что методы обучения решению уравнений на разных этапах освоения предмета имеют много общего, так как, по сути, перед учеником ставится одна и таже задача — подбор числа или чисел, удовлетворяющих данному равенству.
Основы работы с уравнениями закладываются, объясняются на простых математических объектах, пока предмет еще не разделен на алгебру и геометрию. Именно в этом возрасте ребенку отводится время на формирование представление о том, как изучаемый объект устроен и как он используется в реальных ситуациях. Исключение этого важного этапа математической подготовки в большинстве случаев оказывается впоследствии невосполнимым. Даже опытный учитель , работая с учеником старших классов, не сможет в полной мере компенсировать недостаток внимания к уравнениям в младших классах. Можно только дать представление о методах решения или натаскать на заучивание определенных алгоритмов.
Прежде чем говорить об алгоритмах по решению уравнений, давайте вспомним его определение.
Алгоритм – понятное предписание, указывающее, какие операции и в какой последовательности необходимо выполнить с данными, чтобы решить любую задачу данного типа.
Характеристические свойства понятия «алгоритм»:
- Свойство массовости — обеспечивает решение широкого класса задач данного типа;
- Свойство дискретности и элементарности шагов — т.е. разбить на последовательность отдельных шагов, только выполнив один шаг, переходим к другому;
- Свойство результативности — процесс вычисления прекращается за конечное число шагов.
- Свойство детерминированности — запись должна быть полной и четкой, чтобы не было потребности домысливать.
Всякий алгоритм описывает общий метод решения класса однотипных задач.
Правило — «свернутый» алгоритм. Всякий алгоритм можно назвать правилом, но не всякое правило можно назвать алгоритмом.
На своих уроках я выделяю три основных этапа:
- введение алгоритма;
- усвоение алгоритма;
- применение алгоритма.
- цель первого этапа – актуализация знаний, необходимых для введения и обоснования алгоритма, а также формулирование алгоритма;
- цель второго этапа – отработка операций, входящих в алгоритм, и усвоение их последовательности;
- цель третьего этапа – отработка алгоритма в знакомых (при варьировании исходных данных) и незнакомых ситуациях.
Формы работы с учащимися:
- на первом этапе — устная работа на повторение.
- на втором этапе – письменная коллективная работа с широким использованием комментирования выполняемых действий и групповая работа.
- на третьем этапе – самостоятельная работа.
Остановимся подробно на уроке в 5 классе.
5 класс . (см презентацию)
1 этап. Уравнения решаются на основе зависимости между результатом и компонентами арифметического действия.
- a+x=b Правило 1: Чтобы найти неизвестное слагаемое, надо из суммы вычесть
- a – x = b Правило 2: Чтобы найти неизвестное уменьшаемое, надо сложить
вычитаемое и разность.
- x – a = b Правило 3: Чтобы найти неизвестное вычитаемое, надо из уменьшаемого
- x · a=b Правило 4: Чтобы найти неизвестный множитель, надо произведение
разделить на известный множитель.
- x:а=b Правило 5: Чтобы найти неизвестное делимое, надо частное умножить на
- a:х=b Правило 6: Чтобы найти неизвестный делитель, надо делимое разделить на
- 1) x + 37 = 85;
- 2) m – 94 = 18;
- 3) 85 – z = 36;
- 4) 4x = 144;
- 5) x : 8 = 13;
- 6) 42 : x = 6
- 13899 + x = 2716 + 13899
- 4х + 4х = 424
- 15а – 8а = 714
- 8,6 – (x + 2,75) = 1,85
- 45,7х + 0,3х – 2,4 = 89,6
- x + 2,8 = 3,72 + 0,3
Учащиеся 5 класса сначала должны определить неизвестный компонент действия, а затем найти его, пользуясь одним из вышеперечисленных правил.
Заполните пропуски в формулировках и определениях.
- Уравнением называется ____________, содержащее ____________.
- Корнем уравнения называется такое значение ______________, при котором уравнение обращается в _____________ равенство.
- Чтобы найти неизвестное уменьшаемое, нужно к _____________ вычитаемое.
- Чтобы найти неизвестное вычитаемое, нужно _______________ вычесть _______________.
2 этап. Заполните пустые клетки в таблице.
3 этап. Узнайте, какое слово зашифровано в таблице.
Итак, на данном уроке вы сами увидели основные этапы формирования алгоритма решения уравнений.
-Уважаемые учителя, у вас возникли вопросы?
вопрос: Наверное, каждый учитель , слышал жалобы от родителей, связанные со снижением успеваемости при переходе в 6 класс. «Мой ребенок всегда хорошо решал уравнения и вдруг перестал их понимать», — часто жалуются родители. «Что нам делать? Я не могу ему донести то, что понимаю сама», — обычная картина. Как решить эту проблему?
В конце 5-го и в начале 6-ого класса понятие числа расширяется. Появляются уравнения с дробями (десятичными и обыкновенными) и вместе с ними приходят главные проблемы. Как теперь решить такое?
Одна из причин кроется в возрастных особенностях работы памяти ребенка и его мышления, в способности рассмотреть простой объект внутри сложного. В большинстве случаев ученику рано переходить к использованию алгоритмов в более сложных математических объектах.
Во-первых, понимание этих аналогий часто еще не успевает сформираться. Во-вторых, механизмы позволяющие переносить эти операции на более сложные объекты могут быть не отработаны на достаточном количестве заданий. В- третьих, сами операции и правила, по которым они выполняются, часто забываются.
Глубоким заблуждением многих методистов и школьных преподавателей является мнение о том, что правила нахождения компонентов алгебраических действий, просто заученные наизусть, помогают каждому ребенку принять решение о том, сложить ли ему данные числа, или отнять, найти ли разность a-b или b-a. Вспомните себя, всегда ли помогало вам на уроках математики такое правило: чтобы найти вычитаемое, надо из уменьшаемого вычесть разность? Приходится вспоминать названия участников действия, затем текст правила (каждое для своего случая). Пока ученик будет вспоминать текст, — успеет забыть где у него в уравнении стоит уменьшаемое, а где вычитаемое. Начнет вспоминать названия — забудет правило. А еще нужно правильно записать и произвести вычисления. Куда тут до правильного ответа? Укротить бы термины.
Как действует ученик в простом случае и почему он промахивается с подбором действий в более сложных? Дело в том, что к моменту, когда ему необходимо решить уравнение 8-x=3 в пятом классе он, как правило, получает хорошую практику вычислений и просто узнает знакомую картинку, в которой пропущено одно число. Он может и без правил догадаться, какое число ему поставить вместо икса. И если требуется записать действие для его нахождения, он переберет все возможные варианты с числами 8 и 3 (благо они перед глазами) и выпишет подходящее. Никакими правилами нахождения вычитаемого он в большинстве случаев не пользуется. Это слишком сложно для него.
С некоторым напряжением ученику даются уравнения, нагруженные несколькими действиями, например 42: (2х-8)=7. Если числа в таких уравнених не очень большие, то в голове пятиклассника реализуется тот же самый алгоритм подбора неизвестного компонента 2x-8 в делении. Этот алгоритм, обычно, опережает подбор действия, с помощью которого получается ответ. Сложности возникают только с тем, что ребенку приходится находить не икс, а некотороый промежуточный результат. Практика моей работы показывает, что с этим видом непонимния часто удается справиться сравнительно легко. Главная помощь здесь заключается в своевременном повторении понятия «корень уравнения» и «проверка корня». При этом учитель должен уделить внимание практическому ходу этой проверки и выделить в ней определенные этапы:
1) Берем наугад число для проверки
2) Выполняем его умножение на 2, затем вычитаем 8 и получаем некоторый промежуточный результат
3) делим 42 на него и должно получиться 7.
При такой форме ребенок в 95 % случаев сам скажет, что нужно разделить на 6. В этот момент учитель обязательно укажет ученику на то, что подобранное число 6 должно получиться в результате вычитания. Останется понять, как при вчитани числа 8 получить 6. Учитель должен поставить новую цель: что вставить вместо икса, чтобы после умножения на 2 и вычитания восьми эта шестерка получилась. Тогда надо решить уравнение, в котором слева уже стоит не 42: (2х-8)=7, а 2х-8. Этот момент отдельно выделяется и учителю обязательно нужно на нем остановиться отдельно. Решая такими путями уравнения, ребенок запоминиает поведение чисел. Те взаимосвязи, которые предлагабются ему для заучивания запоминаются в естественном порядке, а именно в процессе деятельности.
Существуют простые, но важные правила работы с методикой:
1) Учитель по математике должен исключить из текстов своих пояснений стандартные математические термины и шаблонные фразы («значение выражения», «переменная», «делитель», «значение переменной, при которой. »)
2) При подборе уравнения следует не дупустить проникновение в него повторяющихся действий и даже повторяющихся чисел (как начальной в записи самого уравнения, так и во всех дальнейших формах). Иначе ребенок запутается, о каком делении идет речь в конкретный момент и о каком числе 6 , если она используется дважды.
3) Каждая пара чисел в уравнении на каждом этапе решения должна быть удобной для подбора третьего числа.
Дроби…Подбор числа и действия затрудняется, так как операции с дробями делаются в несколько этапов. Если раньше ребенок мог распознать, что число а не делится на число b , то теперь уже можно делить друг на друга почти все числа. Сложнее узнать знакомое сочетание и подбирать для него соответствующее арифметическое действие. При достаточном количестве решенного ранее, способные дети запоминают алгоритмы и по аналогии применяют их в новой ситуации. А что делать отстающим? У многих из них информация о правилах еще успела прочно отложиться в его долговременной памяти.
В этом случае необходимо продлить время привычной деятельности ученика при решении уравнений. То есть подбирать действия прежним способом. Для этого преподавателю достаточно обязать (или разрешить) рядом с решаемым уравнением составить любой простенький пример на это же действие, но с натуральными числами. Допустим, надо решить уравнение:
Учитель просит ученика определить последнее действие в левой части уравнения, составить с его участием любой простенький пример из программы 2-го класса и записать его где-нибудь рядом.
-3 — (2:х+0,3) =-1 6- 2 =4
Ребенок смотрит, какой учасник последнего действия в исходном уравнении неизвестен, находит его аналог в придуманном примере и по нему подбирает арифметическое действие с соседними числами (благо они перед глазами). Затем просто переносит его на свое уравнение. И так с каждым исключением последнего действия. Полное оформление может выглядеть следующим образом:
-3 — (2:х+0,3) = -1 6- 2 =4
Ученик должен помнить, что в составленных примерах числа не повторялись. Не стоит cоставлять такие примеры:
и подобные им . 6-3=3 5+5=10
Для совсем слабых детей учитель может заготовить отдельные карточки с уже подобранными примерами на все действия и класть их перед учеником в нужный момент.
Вернемся к основной теме.
Общий приём решения уравнений:
слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак.
«Универсальный» алгоритм решения линейных уравнений с одним неизвестным вида:
1) раскрыть скобки (если таковые имеются);
2) оставить неизвестные в одной части уравнения, известные – в другой (уединение неизвестных);
3) привести подобные слагаемые;
4) разделить обе части уравнения на коэффициент при неизвестном;
5) записать ответ.
Пример: 5х + 3 = 2х + 9
Первый этап формирования алгоритма
Устные упражнения на повторение:
1) Перенесите из левой части уравнения в правую то слагаемое, которое не содержит неизвестного:
а) 8х + 5,9 = 7х + 20;
б) 6х – 8 = -5х – 1,6.
2) Оставьте в левой части уравнения все слагаемые, содержащие неизвестное, а в правой – не содержащие неизвестное:
а) 15y – 8 = -6y +4,6;
б) -16z + 1,7 = 2z – 1.
3) Приведите подобные слагаемые:
а) 15t + 8 – 8t – 6;
б) 13a + 4 – 7a — 25a;
в) 24m + 7 – 9m – 14m.
4) Раскройте скобки и приведите подобные слагаемые:
Первый вид тестовых заданий:
1. Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», _________________ знаки слагаемых, стоящих в скобках.
2. Раскройте скобки:
-17,5 + (3,02 – 2,51) = __________________.
3. -(a + b) = __________________.
4. Коэффициентом такого выражения, как a или ab, считают _________.
5. Слагаемые, имеющие одинаковую буквенную часть, называют ______________________ слагаемыми.
6. Выполните приведение подобных слагаемых:
- b – 2c + 4b – c = _________________________.
7. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то корни уравнения ________________________.
Второй вид тестовых заданий:
1. Выражение a + (b + c) можно записать без скобок:
a + (b + c) = a + b + c
2. Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
3. Приведение подобных слагаемых выполняют на основании переместительного свойства умножения.
4. Число -30 является корнем уравнения
Третий вид тестовых заданий:
1. Раскройте скобки в выражении: a – (b + c — d)
2. Найдите значение выражения: 25 – (12 — 53)
3. Упростите: 5x – 5y – 6x + y
4. Найдите корень уравнения: 4 – 3y = 7 — y
Второй этап формирования алгоритма
1) -2x + 16 = 5x – 19
2) 4(3 – 2x) + 24 = 2(3 + 2x)
4) 0,5(4 + x) – 0,4(x — 3) = 2,5
5) 0,4(x — 9) – 0,3(x + 2) = 0,7
Третий этап формирования алгоритма
1. Решите уравнение: 4,2х + 5 = -7,6
2. Найдите сумму корней уравнений
х + 11,7 = 8,7 и (3х + 4,6) – 6,6 = 8,7 + 2,2
3. Отец в два раза старше сына и на 25 лет старше дочери. Сколько лет дочери, если всем вместе им 95 лет?
1. Решите уравнения:
б) 2(4 – 1,9х) = 0,8 – 0,2х.
2. На верхней полке в 3 раза больше книг, чем на нижней. После того, как с верхней полки сняли 15 книг, а на нижнюю добавили 11 книг, книг на обеих полках стало поровну. Сколько книг было на каждой полке первоначально?
3. Путь из города в село турист прошел со скоростью 4,8 км/ч. На обратном пути он увеличил скорость до 6 км/ч, что позволило ему пройти это расстояние на 1 час быстрее. Найдите расстояние от города до села.
Алгоритм решения линейного уравнения с двумя переменными типа: 5y – 2x = 1
1) воспользовавшись свойствами уравнений, выразить из данного уравнения одну переменную через другую;
2) воспользовавшись свойствами уравнений, добиться того, чтобы коэффициент при одной из переменных был равен единице;
3) взять произвольное значение одной из переменных и вычислить соответствующее ему значение другой переменной;
4) записать решение исходного (данного) уравнения в виде пары (пар) чисел.
если x = 2, то 6-1,5*2 = 6 – 3 = 3;
если x = 6, то 6-1,5*6 = 6 – 9 = -3.
Пары чисел (2; 3), (6;-3) – решение уравнения (1).
уравнение (1) имеет бесконечно много решений
Тестовые задания по теме: «Уравнение с одной переменной»
1. Выберите уравнения, для которых число -3 является корнем:
1) (2x + 3)(2x — 6) = 0; 3) (2x + 6)(x — 4) = 0;
2) (x2 — 9) + (x2 — 7) = 2; 4) (x + 3)(x2 – 3x + 9) = 0.
а) 1; 2; б) всех; в) 3; 4; г) 2; 3; 4.
2. Найдите все натуральные значения p, при которых корнем уравнения px = 8 является целое число.
а) 1; 2; 4; 8; б) 1; 8; в) 2; 4; г) 2; 4; 8.
3. При каком значении c пара (c;3) является решением уравнения
4. Точка с абсциссой -3 принадлежит графику уравнения x – 2y = 10. Найдите ординату этой точки.
а) -6,5; б) 6,5; в) 4; г) -4.
Тестовые задания по теме «Уравнения с двумя переменными»
1. При каком значении c пара (c;3) является решением уравнения
2. Точка с абсциссой -3 принадлежит графику уравнения x – 2y = 10. Найдите ординату этой точки.
а) -6,5; б) 6,5; в) 4; г) -4.
1. Решите уравнения:
2. Определите значение x, при котором значение выражения -3х равно:
3. При каких значениях a уравнение ax = 8:
1) имеет корень, равный -4, 0;
2) не имеет корней;
3) имеет отрицательный корень.
Ну, а теперь давайте подведем итоги.
Можно ли научить решать любое уравнение?
Ответ неоднозначен. Ясно, что рассчитывать на изображение методики обучения решению уравнений, пригодной для всех детей и во всех случаях – все равно, что искать универсальное лекарство от всех болезней. Практическая ценность обучения школьников решению уравнений разнообразными способами в современных условиях заключается совсем не в том, чтобы раз и навсегда вооружить их приемами решения различных уравнений, которые будут возникать в дальнейшем обучении, а в том, что оно обогатит их опыт мыслительной деятельности. А помогут в этом алгоритмы решения уравнений.
Так каким же должен быть алгоритм?
Методические рекомендации по организации работы учащихся с алгоритмами и формированию алгоритмического мышления.
- алгоритм должен быть по возможности наиболее кратким;
- «Читая и применяя алгоритм, старайтесь запоминать его»;
- пунктуационное соблюдение данного учителем образца решения задачи;
- указания в алгоритме желательно давать в таком виде, чтобы они содержали в себе все необходимые объяснения, какие учитель хочет слышать от учащихся по ходу решения задач.
Методические рекомендации по решению иррациональных уравнений и неравенств.
В работе даны методические рекомендации по решению иррациональных уравнений и неравенств. Предложен материал для самостоятельного решения
Просмотр содержимого документа
«Методические рекомендации по решению иррациональных уравнений и неравенств.»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ МУРМАНСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ МУРМАНСКОЙ ОБЛАСТИ
«КАНДАЛАКШСКИЙ ИНДУСТРИАЛЬНЫЙ КОЛЛЕДЖ»
Методические рекомендации к практическим работам по теме «Решение иррациональных уравнений и неравенств»
Разработала преподаватель математики
1категории Гашимова А.Н.
Практические занятия — один из видов практического обучения, имеющий целью закрепление теоретических знаний и формирование практических умений и навыков.
Практическая работа по математике заключается в выполнении студентами под руководством преподавателя комплекса учебных заданий, направленных на усвоение основ учебной дисциплины «Математика», приобретение практических навыков решения примеров и задач. Выполнение практической работы студенты производят в письменном виде, оформляя отчеты в тетради. Отчет предоставляется преподавателю для проверки.
Практические занятия способствуют более глубокому пониманию теоретического материала учебного курса, а также развитию, формированию и становлению различных уровней составляющих профессиональной компетентности студентов, пониманию межпредметных связей. Основой практикума выступают типовые задачи, которые должен уметь решать студент, изучающий дисциплину «Математика».
Для лучшего усвоения студентами изучаемого материала и получения уверенных навыков решения примеров и задач при проведении практических занятий целесообразно использовать различные методы и приемы:
— рассмотрение решения типовых примеров;
— исследовательская работа при решении примеров и практических задач;
— работа в группах;
Содержанием практических занятий являются
— Выполнение вычислений, расчетов;
— Работа со справочниками, таблицами.
Необходимые структурные элементы практического занятия:
— Инструктаж, проводимый преподавателем;
— Самостоятельная деятельность студентов;
— Анализ и оценка выполненных работ и степени овладения студентами запланированных умений.
Перед выполнением практического занятия проводится проверка знаний студентов на предмет их готовности к выполнению задания.
Оценки за выполнение являются показателями текущей успеваемости студентов по дисциплине «Математика».
Критерии оценки практических заданий.
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна существенная ошибка или два-три несущественных ошибки.
Отметка «3» ставится, если:
допущены более одной существенной ошибки или более двух-трех
несущественных ошибок, но студент владеет обязательными
умениями по проверяемой теме; при этом правильно выполнено не
менее половины работы.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что студент не владеет
обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у студента обязательных знаний и
умений по проверяемой теме или значительная часть работы выполнена
К категории существенных ошибок следует отнести ошибки, связанные с незнанием, непониманием студентом основных положений теории и с неправильным применением методов, способов, приемов решения практических заданий, предусмотренных программой.
К категории несущественных ошибок следует отнести погрешности, связанные с небрежным выполнением записей, рисунков, графиков, чертежей, а также погрешности и недочеты, которые не приводят к искажению смысла задания и его выполнения.
При наличии существенной ошибки задание считается невыполненным.
Цель практических занятий: познакомить студентов с решением некоторых типов иррациональных уравнений; способствовать развитию навыка решения иррациональных уравнений и неравенств.
Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.
Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. При решении иррациональных уравнений применяют метод возведения в степень обоих частей уравнения и метод введения новой переменной (замены переменной).
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному.
При возведении уравнения в четную степень получается уравнение, являющееся следствием исходного. В связи с этим возможно появление посторонних решений уравнения, но не возможна потеря корней. В этом случае обязательна проверка найденных корней подстановкой в исходное уравнение.
Мощным средством решения иррациональных уравнений является метод введения новой переменной, или «метод замены». Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную. В ряде случаев удачно введенные новые неизвестные иногда позволяют получить решение быстрее и проще; иногда же без замены решить задачу вообще невозможно.
Иногда удобнее решать иррациональные уравнения, определив область допустимых значений и используя равносильные переходы.
Рассмотрим применение данных методов решения иррациональных уравнений.
Пример 1. Решите уравнение 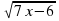
Решение. Возведем обе части этого уравнения в квадрат и получим: 7х-6= х 2 . Решаем квадратное уравнение: х 2 — 7х+ 6 =0
Проверяем полученные результаты, подставляя в начальное условие:
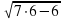
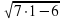
Пример 2. Решить уравнение 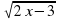
Решение. Возведем обе части в квадрат: 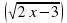
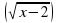
Проверка: 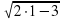
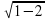
Ответ: решений нет
Пример 3. Решить уравнение 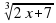
Решение: 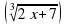
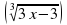
В даннам случае проверка необязательна, так как использовался метод возведения обеих частей в нечётную степень, при которой посторонние корни не появляются.
Пример 4. Решить уравнение 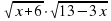
Решение. Возведем обе части уравнения в квадрат 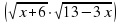
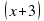
13х- 3х 2 +78 -18х = х 2 + 6х +9;
х1= 3; х2=- 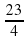
Проверка: х1= 3: 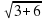
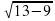
х2=- 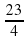
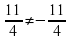
Пример 5. Решить уравнение 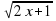
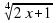
Решение. Введем новую переменную. Пусть 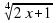
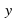
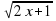
Получаем новое уравнение: у 2 +у -12=0; у1=3; у2=- 4.
1) 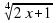
2) 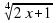
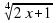
Пример 6. Решить уравнение 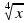
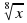
Решение. Пусть 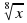
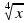
Получим у 2 + у — 2 =0; у1=- 2; у2=1.
1) 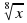
2) 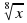
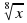
Пример 7. Решить уравнение 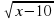
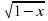
Решение. Область допустимых значений неизвестного (ОДЗ) определяется системой неравенств 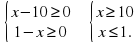
Ответ: нет решений.
Задания для индивидуальной и групповой работы.
1. 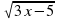
2. 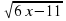
3. –х – 5=
4. 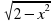
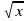
5. 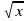
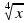
6. 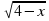
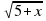
7. 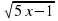
Методические рекомендации по изучению тем: 1. Квадратные уравнения. 2. Квадратичная функция. 3. Квадратные неравенства методом УДЕ
Разделы: Математика
Введение
| “Противопоставление облегчает и ускоряет наше здоровое мышление” |
Академик И.Павлов
Академик И. Пригожин
Все согласны с тем, что нет “царского пути в математику”. Много труда в терпения, настойчивости и внимания требуется от учителя и школьника, чтобы последний смог освоить программный минимум знание по этому предмету.
Мы привыкли сейчас к открытиям, одно поразительнее другого:
- изобретены лазеры и голография;
- расшифрован код наследственности;
- синтезирован ген;
- научались выращивать копии животных.
Недалеко, видимо, то время, когда и в психологии в педагогике будут найдены такие средства обучения, эффективность которых трудно сейчас представить.
Н.Е. Жуковский имел основания считать, что методы обучения математике можно сделать столь совершенными, что ее будет понимать “всякий желающий из публики”.
Добиться того, чтобы человек за меньшее, чем прежде, время овладел большим объемом основательных и действенных знаний, – такова одна из главных забот современной педагогики.
Нередко структура учебника математики определяет лишь формально – логическими связями самой науки математики, вне учета закономерностей усвоения математических знаний.
Между тем средства формальной логики ограничены, они упорядочивают отвлеченные результаты мышления, но никак не сам процесс мышления, к этим результатам приводящий.
Формально – логические соображения не только не являются единственными, но и не являются главными при решении вопросов методики: дело в том, что категории формальной логики не учитывают фактора времени, учет которого являются важнейшем элементом для совершенствования процесса обучения.
Как при изобретении новых механизмов, так и при конструировании новых методов обучения исходным толчком к удачным находкам и обобщениям могут стать соображения, связанные с любой из указанных наук. Это человек для удобства создал разные науки, а “природа не знает деления на науки”.
Укрупненная дидактическая единица – это клеточка учебного процесса, состоящая из логически различных элементов, обладающих в то же время информационной общностью. Укрупненная дидактическая единица обладает качествами системности и целостностями, устойчивостью к сохранению во времени и быстрым проявлением в памяти.
Понятие укрупнения единицы усвоения достаточно общо, оно вбирает следующие взаимосвязанные конкретные подходы к обучению:
- совместное и одновременное изучение взаимосвязанных действий, операций, функций теорем и т.п. (в частности, взаимно обратных);
- обеспечение единства процессов составления и решения задач (уравнений, неравенств т.п.);
- рассмотрение во взаимопереходах определенных и неопределенных заданий (в частности, деформированных упражнений);
- обращение структуры упражнения, что создает условия для противопоставления исходного и преобразованного заданий;
- выявление сложной природы математического знания, достижение системности знаний;
- реализация принципа дополнительности в системе упражнений (понимание достигается в результате межкодовых переходов между образным и логическим в мышлении, между его сознательным и подсознательным компонентами).
Общность выводов теоретического анализа позволяет предвидеть и выгоды переноса указанной методической системы с младших классов на старшие, с математики на друга учебные предметы, от школьной практики в вузовскую дидактику.
Фактором, обеспечивающим высокое качество укрупненного знания, может выступить:
- общий графический образ;
- общность символов для группы формул;
- наличие одних и тех же слов или словосочетаний в сравниваемых высказываниях, в цепи доказательств и в ткани развивающихся системных знаний, предыдущие и последующие во времени звенья должны иметь, как правило, больше общих носителей информации, начиная, с возможно более низкого, кода.
Цели: формирование умения решать квадратные уравнения и неравенства, строить графики квадратичных функций, развитие самостоятельного и творческого мышления, воспитание самостоятельной и творческой личности, потребности к учению.
Задачи:
- изучить одновременно взаимообратные действия и операции;
- обеспечить единство процессов составления и решения уравнений, неравенств;
- сформировать общеучебные, интеллектуальные практические умения.
Тематическое планирование курса алгебры 8-го класса
(3 ч. в неделю, всего 102 часа)
Сейчас существует множество учебников я методических рекомендаций по изучению “Алгебры 7-11 кл.”. Учителю в данной сфере важно выбрать для своих учеников наиболее оптимальный и адаптированный вариант для контингента учащихся данного класса. А самое главное, расположить изучаемый материал в логической последовательности, чтобы повысить эффективность и качество усвоения изучаемого материала. Так например, можно укрупнить и преподать в логической цепи такие темы “Линейная функция. Решение линейных уравнений и неравенств. Решение систем линейных уравнений и неравенств”. Мне бы хотелось остановиться на изложении следующих тем “Квадратные уравнения Квадратичная функция. Квадратные неравенства”.
Примерное тематическое планирование курса алгебры 8 класса
(3 часа в неделю, всего 102 часа)
|
Планирование тем в такой последовательности предусматривает работу учащихся 8 классов по учебнику О.П. Эрдниева, П.М. Эрдниева “Математика” 8 класс.
Изучение темы “Квадратные уравнения” начинается с III четверти, на которую я отвожу – 20ч.
| – 3 ч. – 4 ч. – 4 ч. – 3 ч. – 4 ч – 1 ч. – 1 ч. |
Важно, что на обобщающем уроке учащиеся вместе с учителем систематизируют и упорядочивают всю информацию по решению квадратных уравнений, заполнив следующую таблицу:
Виды квадратных уравнений
ах2+bx+c=0
неполным
приведенным
полным
Формулы корней квадратных уравнений
x(ax+b)=0
x1=0, или x2=-b/a
(2-а корня)
2. ax 2 +c=0
ax 2 =-c
x 2 =-c/a
x1,2= ±
если –c/a >0
(2 корня)
если –c/a 0
ax 2 -c=0
x 2 -c/a=0
(x-

x1=- 
x1,2=-p/2±
если p 2 /4-q>0, то 2 корня
если p 2 /4-q=0, то 1 корень
если p 2 /4-q 2 +bx+c=0
x1,2=
b 2 -4ac=D – называется дискриминант
если D>0, то 2 корня
если D=0, то 1 корень
если D 2 +px+q=0
x1+x2=-p
x1? x2=q
a
a
x1+x2=-b/a
x1? x2=c/b
На изучение темы “Квадратичная функция” отвожу 17 часов и распределяю материал следующим образом:
| 2 часа 4 часа 4 часа 2 часа 3 часа 1 час 1 час |
Можно изучение квадратичной функции вида у = ах 2 провести в форме лабораторной работы. Урок можно построить следующим образом.
Урок №1-2
Тема: Функция у = ах 2
Цель: Построение функции у = ах 2 , свойства данной функции; построение графиков функции вида у = ах 2 , изучение влияния значения коэффициента а на форму и расположение параболы.
Ход урока
1. Построение графика функции у = ах 2 , изучения ее свойства
Рассмотрим функцию у = ах 2 , то есть квадратичную функцию у = ах 2 +bх+с при a= 1, b =с = 0. Для построения графика этой функции составим таблицу ее значений:
| x | ± 4 | ± 3 | ± 2 | ± 1 | ± 0,5 | 0 |
| y=ax 2 | 16 | 9 | 4 | 1 | 0,25 | 0 |
Построив указанные в таблице точки и соединив их плавной кривой, получим график функции у = ах 2 .
Кривая, являющаяся графиком функции у = ах 2 , называется параболой.
Рассмотрим свойства функции у = ах 2 .
- значениями аргумента (абсциссами) могут быть любые числа. Говорят, областью изменения аргумента является множество действительных чисел;
- график функции у = ах 2 симметричен относительно оси ординат, то есть, ось ординат является осью симметрии параболы;
- парабола у = ах 3 проходит через начало координат, то есть, парабола у = ах 3 касается оси абсцисс в точке (0;0), которая является вершиной параболы;
- функция у = аx 2 является возрастающей на промежутке х>0.
- функция у = ах 2 является убывающей на промежутке х 2
Цель: изучение влияния значения коэффициента а на форму и расположение параболы.
Оборудование:
- Матрица “Расположение и форма параболы у = ах 2 в зависимости от значения коэффициента а”.
- Таблицы функции у = х 2 , у = 2х 2 , у = 0,5х 2 .
- Маркеры трех цветов (красный, зеленый, синий).
I часть
1. Построить таблицу значений функций у = ах 2 , а>0.
| a) y=0,5x 2 | b) y=x 2 | c) y=2x 2 |
| аргумент | x | 0 | ± 1 | ± 2 | ± 3 | значение a |
| функция | y=ax 2 | |||||
| (e1) | y=0,5x 2 | 0 | 0,5 | 2 | 4,5 | a=0,5 |
| (e2) | y=x 2 | 0 | 1 | 4 | 9 | a=1 |
| (e3) | y=2x 2 | 0 | 2 | 8 | 18 | a=2 |
2. Построим на одном чертеже графики трех данных функция е1 – у=0,5х 2 – синим цветом; е2— у=х 2 – красным цветом; и е3 – у=2x 2 – зеленым цветом.
3.. Учащееся сравнивают положение графиков функции вида у = ах 2 (а>0) и отмечают чем похожи все три параболы:
а) они имеют одинаковую форму;
б) ветви парабол неограниченно стремятся ветвями вверх;
в) ветви всех парабол симметричны относительно оси ординат 0у;
г) все эти параболы имеют самую низкую общую точку (0; 0), т.е. функция имеет минимум.
4. Чем отличаются положения графиков функций вида функции у = ах 2 (а>0):
функция вида у=ах 2 (а>О) возрастает тем круче (а соответствующая парабола тем быстрее поднимается вверх), чем больше коэффициент при х 2
II часть
5. Сравнить графики двух функций вида у = ах 2 (например, у = 0,5 х 2 и у = – 0,5 х 2 ), у которых коэффициентами а являются противоположные числа 0,5 и – 0,5.
6. Построить таблицу значений функций у = 0,5х 2 и у = -0,5х 2
| Абсцисса | 0 | ±1 | ±2 | ±3 | ±4 |
| y=0,5x 2 (e1) | 0 | 0,5 | 2 | 1,5 | 8 |
| y=-0,5x 2 (e1 1 ) | 0 | -0,5 | -2 | -1,5 | -8 |
7. Достроим в той же таблице недостающий график функции у = -0,5х 2 (см. таблицу)
8. Сравнить положения графиков функции у = 0,5х 2 и y=-0,5x 2
а) точка О (0; 0) есть самая низшая точка параболы у = 0,5 х 2 и наибольшая параболы у=-0,5х 2
б) графики (e1 и e1 1 ) двух функций у = 0,5х 2 и у = – 0,5х 2 симметричны друг другу относительно оси абсцисс.
9. Чем отличаются положение графиков функций вида у=0,5x 2 ,у=-0,5х 2
Запомним важное правило:
Если в уравнении квадратичной функции у=ах 2 коэффициент
Верно и обратное:
Если парабола стремится ветвями 
y=0,5x 2
y=x 2
y=2x 2
После прохождения всех способов построения графика функции у =ах 2 +bх+с переносом графика функции у=ах 2 можно провести урок по решению взаимно обратных задач: по заданному графику составить уравнение функции и обратные задачи – это по заданному уравнению функции у = ах 2 +bх+с построить её график. На этом же уроке необходимо завершить работу над матрицей “Взаимное расположение квадратной функции у=ах 2 +bх+с относительно оси абсцисс”.
Урок №10
Тема: Построение графика функций у=ах 2 +bх+с переносом графика функций у=ах 2
Цель:
- Закрепление навыков учащихся по построению графиков функций вида у=ах 2 +bх+с, выполнение обратных задач, завершение работы над матрицей.
- Формирование умения выделять существенные признаки и свойства функция вида у=ах 2 +bх+c и построение её графика
- Воспитание положительного отношения к знаниям.
I. Устная работа
- Назовите основные свойства функции у=ах 2 ?
- Как можно записать квадратичную функцию?
- Что значит, построить график функции у=ax 2 +bx+c?
- Что нужно вычислять в первую очередь при построении графика функции у=ax 2 +bx+c?
- Сколько вы знаете способов их нахождения?
II. Выполнение заданий на чтение графиков
Задача: По заданному графику составить уравнение функции. (У доски работают трое учащихся, выполняют задания по трём заданным графикам).
http://kopilkaurokov.ru/matematika/prochee/mietodichieskiie_riekomiendatsii_po_rieshieniiu_irratsional_nykh_uravnienii_i_ni
http://urok.1sept.ru/articles/563185