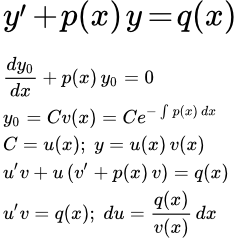Методом лагранжа можно решить уравнение

Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.

Метод вариации постоянной (Лагранжа)

В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.

Шаг 1 Решение однородного уравнения

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные — умножаем на dx , делим на y :

Интегрируем:

Интеграл по y — табличный:

Тогда

Потенцируем:

Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1 , которую включим в C :

Шаг 2 Заменим постоянную C на функцию

Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.

По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:

.
Подставляем в исходное уравнение (1):
(1) ;

.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа

Решаем однородное уравнение:

Разделяем переменные:

Умножим на :

Интегрируем:

Интегралы табличные:

Потенцируем:

Заменим постоянную e C на C и убираем знаки модуля:

Отсюда:

Заменим постоянную C на функцию от x :
C → u ( x )

Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.

Общее решение уравнения:
.

Автор: Олег Одинцов . Опубликовано: 27-07-2012 Изменено: 01-03-2015

Метод вариации произвольной постоянной решения линейных неоднородных уравнений

Пример №1 . Найдём общее решение уравнения y» + 4y’ + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y» + 4y’ + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y₁ = e — x и y₂ = e -3 x . Решение неоднородного уравнения ищем в виде y = C₁(x)e — x + C₂(x)e -3 x . Для нахождения производных C’₁, C’₂ составляем систему уравнений (8)
C′₁·e -x +C′₂·e -3x =0
-C′₁·e -x -3C′₂·e -3x =9e -3x
решая которую, находим , Интегрируя полученные функции, имеем
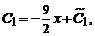
Окончательно получим

Пример №2 . Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:

y(0) =1 + 3ln3
y’(0) = 10ln3

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4

Корни характеристического уравнения: r₁ = 4, r₂ = 2
Следовательно, фундаментальную систему решений составляют функции: y₁=e 4x , y₂=e 2x
Общее решение однородного уравнения имеет вид: y =C₁·e 4x +C₂·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C′₁·e 4x +C′₂·e 2x =0
C′₁(4e 4x ) + C′₂(2e 2x ) = 4/(2+e -2x )
Выразим C’₁ из первого уравнения:
C’₁ = -c₂e -2x
и подставим во второе. В итоге получаем:
C’₁ = 2/(e 2x +2e 4x )
C’₂ = -2e 2x /(e 2x +2e 4x )
Интегрируем полученные функции C’_i:
C₁ = 2ln(e -2x +2) — e -2x + C * ₁
C₂ = ln(2e 2x +1) – 2x+ C * ₂

Поскольку y =C₁·e 4x +C₂·e 2x , то записываем полученные выражения в виде:
C₁ = (2ln(e -2x +2) — e -2x + C * ₁) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x
C₂ = (ln(2e 2x +1) – 2x+ C * ₂)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₁ e 4x + C * ₂ e 2x

Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3

Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * ₁ + C * ₂ = 3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C₁ e 2x + C₂ -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C₁ + C₂ +4 ln(3)+ ln(3)-2) = 4C₁ + 2C₂ +10 ln(3) -4 = 10ln3

Получаем систему из двух уравнений:
3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
4C₁ + 2C₂ +10 ln(3) -4 = 10ln3
или
C * ₁ + C * ₂ = 2
4C₁ + 2C₂ = 4
или
C * ₁ + C * ₂ = 2
2C₁ + C₂ = 2
Откуда: C₁ = 0, C * ₂ = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x

Уравнение Лагранжа

Вы будете перенаправлены на Автор24

Общий метод решения уравнения Лагранжа

Предположим, что некоторое дифференциальное уравнение первого порядка $F\left(x,y,y’\right)=0$, не разрешенное относительно производной, удалось разрешить относительно $y$, то есть представить в виде $y=f\left(x,y’\right)$.

Частным случаем дифференциального уравнения такого вида является уравнение Лагранжа $y=x\cdot \phi \left(y’\right)+\psi \left(y’\right)$, в котором $\phi \left(y’\right)\ne y’$.

Дифференциальное уравнение Лагранжа решают методом введения параметра $y’=p$.

При этом исходное дифференциальное уравнение можно переписать в виде $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$.

Выполнив дифференцирование по $x$ с учетом $dy=p\cdot dx$, после несложных алгебраических преобразований получаем линейное дифференциальное уравнение относительно функции $x\left(p\right)$ и её производной $\frac $, а именно: $\frac -\frac<\phi '\left(p\right)>\cdot x=\frac<\psi '\left(p\right)>$.

Это уравнение решается известным методом, в результате чего получим его общее решение $x=F\left(p,C\right)$.

Подставив полученный результат в соотношение $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$, получим $y=F\left(p,C\right)\cdot \phi \left(p\right)+\psi \left(p\right)$.

Дополнительные частные либо особые решения уравнения Лагранжа могут быть получены в результате нахождения действительных корней уравнения $p-\phi \left(p\right)=0$ и подстановки их в $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$.

Решение типичных задач

Решить дифференциальное уравнение $y=-x\cdot y’+y’^ <2>$.

Имеем дифференциальное уравнение Лагранжа, в котором $\phi \left(y’\right)=-y’$ и $\psi \left(y’\right)=y’^ <2>$.

Вводим параметр $y’=p$ и получаем $y=-x\cdot p+p^ <2>$, а также $\phi \left(p\right)=-p$ и $\psi \left(p\right)=p^ <2>$.

Теперь получим уравнение вида $\frac -\frac<\phi '\left(p\right)>\cdot x=\frac<\psi '\left(p\right)>$. Для этого находим: $\phi ‘\left(p\right)=-1$; $\psi ‘\left(p\right)=2\cdot p$; $p-\phi \left(p\right)=p-\left(-p\right)=2\cdot p$.

Уравнение приобретает вид: $\frac +\frac<1> <2\cdot p>\cdot x=1$.

Применяем алгоритм решения линейного неоднородного дифференциального уравнения:

1. Стандартный вид $\frac+\frac<1><2\cdot p>\cdot x=1$, где $P\left(p\right)=\frac<1><2\cdot p>$, $Q\left(p\right)=1$.
2. Вычисляем интеграл $I_ <1>=\int P\left(p\right)\cdot dp =\int \frac<1><2\cdot p>\cdot dp =\frac<1><2>\cdot \ln \left|p\right|$.

Записываем частное решение $v\left(p\right)=e^<-\frac<1> <2>\cdot \ln \left|p\right|> $, выполняем упрощающие преобразования: $\ln v\left(p\right)=-\frac<1> <2>\cdot \ln \left|p\right|$; $\ln \left(v\left(p\right)\right)^ <2>+\ln \left|p\right|=0$; $\left(v\left(p\right)\right)^ <2>\cdot \left|p\right|=1$.

Выбираем для $v\left(p\right)$ простейший ненулевой вариант: $v\left(p\right)=\frac<1> <\sqrt

> $.