Методы моделирования гидродинамики Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Фаттахаев Р.М., Назаров А.А., Поникаров С.И.
В данной статье рассмотрены различные модели задач гидродинамики , описаны их особенности и на чем основаны эти модели.
Похожие темы научных работ по математике , автор научной работы — Фаттахаев Р.М., Назаров А.А., Поникаров С.И.
This article describes the various models of problems of hydrodynamics are described and their features based on what these models.
Текст научной работы на тему «Методы моделирования гидродинамики»
Р. М. Фаттахаев, А. А. Назаров, С. И. Поникаров
МЕТОДЫ МОДЕЛИРОВАНИЯ ГИДРОДИНАМИКИ
Ключевые слова: моделирование, гидродинамика.
В данной статье рассмотрены различные модели задач гидродинамики, описаны их особенности и на чем основаны эти модели.
Keywords: modeling, hydrodynamics.
This article describes the various models ofproblems of hydrodynamics are described and their features based on what these models.
Фундаментальные уравнения динамики жидкости и газа основаны на универсальных законах: сохранения массы, сохранения количества движения и сохранения энергии. Уравнение, получающееся в результате применения закона сохранения массы к потоку жидкости, называется уравнением неразрывности. Закон сохранения количества движения — это второй закон Ньютона. Его применение к потоку жидкости дает векторное уравнение, известное как уравнение количества движения или как уравнение импульса. Закон сохранения энергии тождественен первому закону термодинамики и в динамике жидкости и газа уравнение, являющееся его выражением, называется уравнением энергии. Для замыкания систем к уравнениям, полученным из упомянутых выше законов сохранения, следует добавить соотношения, устанавливающие связь между свойствами жидкости. Примером такого соотношения может быть уравнение состояния, связывающие термодинамические параметры жидкости: давление р, плотность р и температуру Т. [1].Эту систему уравнений принято называть уравнениями Навье-Стокса.
Для примера запишем систему уравнений для неизотермического (с теплообменом) течения несжимаемой жидкости в декартовых прямоугольных координатах. Она будет состоять из уравнений неразрывности (1), движения (2), и энергии (3).
В данных уравнениях I есть результирующий вектор массовых сил, V -кинематическая вязкость среды ^=ц/р), а -коэффициент температуропроводности (а=Х/рер). В тензорных обозначениях она будет выглядеть как:
В наиболее общем случае система уравнений Навье-Стокса включает всебя уравнения неразрывности, движения и энергии. Если впотоке происходят химические реакции, задача усложняется введениемуравнений модели
турбулентного течения жидкости обуславливается введением дополнительных уравнении.
Уравнения Навье-Стокса могут быть решены в общем виде лишь внекоторых случаях и при ряде допущении. Общего аналитического решениясистемы этих уравнении пока не получено. При этом численные методырешения уравнении Навье-Стокса развиты довольно хорошо и насегодняшнии день нашли широкое применение в различных областях науки итехники. Численное моделирование является неотъемлемои частью процессапроектирования летательных аппаратов, двигательных установок, ракетноитехники, автомобилеи и т. д.
В настоящее время развиты три основных подхода к численномурешению уравнении Навье-Стокса. Первыи из них носит название Методаконечных разностеи. По-англииски -FiniteDifferenceMethod (FDM). Егосуть заключается в прямои замене производных, входящих в исходныеуравнения, их дискретными (разностными) аналогами. Решение ищется вузлах сетки, на которую разбивается расчётная область. Достоинствомметода является относительная простота реализации, при этом, однако, с точки зрения физического смысла этот метод не очень нагляден. Другимнедостатком этого метода являются особые требования к построению сетки, что часто усложняет процесс решения.
Второи называется Методом конечных объёмов или методомконтрольного объёма. В англоязычнои литературе он называется Finite VolumesMethod (FVM). Основа метода заключается в том, что расчётнаяобласть с помощью сетки разбивается на совокупность конечных объёмов. Узлы, в которых ищется решение, находятся в центрах этих объёмов. Длякаждого
объёма должны выполняться законы сохранения массы, количества, движения и энергии. То есть, например, изменение во времени массы среды вконтрольном объёме может происходить только за счёт внешнего потокамассы, входящего в объём, или за счёт потока массы из данного объёма выходящего. Метод конечных объёмов применяется во многих вычислительных гидродинамических (CFD) пакетах, таких как FlowVision, ANSYS Flotran, Flow3d, PHOENICS и ряде других [2].
Третий метод решения — Метод Конечных Элементов (МКЭ). Ванглоязычной литературе его называют FiniteElementsMethod (FEM). Сутьметода состоит в приближенном решении вариационной задачи. Для формулировки этой задачи применяют понятие функционала. Оператор I[f(x)] называется функционалом, заданным на некотором множестве функций, есликаждой функции f(x) ставится в соответствие определённое числовое значение I[f(x)]. Иными словами, функционал является как бы «функциейот функции». Часто функционалы имеют вид интегралов. Вариационнаязадача состоит в отыскании такой функции f(x), которой бы соответствоваломинимальное значение
функционала I[f(x)]. Вид этого функционала различендля различных задач и подбирается специально [3].
В настоящее время Метод Конечных Элементов нашёл широкоеприменение при решении задач теплопроводности в твёрдых телах и прирасчётах на прочность. Однако он может быть применён и к задачам теченияжидкостей и газов. Известны также методы, которыесочетают в себе черты метода конечных объёмов и метода конечныхэлементов. Сочетание этих методов
позволяет использовать болееширокий ряд расчётных сеток (тетраэдрические сетки, пирамиды, призмы, полиэдры), что необходимо при решении задач со сложной геометрией. Этот подход используют CFD пакеты Ansys CFX, AnsysFluent, Star-CD, Star-CCM+ [4].
Итак, подводя итоги проведенного анализа можно сказать, что уравнения Навье-Стокса являются одними из важнейших в гидродинамике. На данный момент не найдено общего аналитического решения системы и это является одной из семи главных «проблем тысячелетия». Решение уравнений усложняется их нелинейностью, турбулентностью,
сжимаемостью среды и зависимостью от начальных и граничных условий. Однако численное моделирование довольно успешно используется во многих природных явлениях и технических задачах.
1. Харламов С.Н. Алгоритмы при моделировании гидродинамических процессов. — Томск. Изд-во ТПУ, 2008. — 80с.
2. Аникеев, А. А. Основы вычислительного теплообмена и гидродинамики: учебное пособие /А. А. Аникеев, А. М. Молчанов, Д. С. Янышев. — М.: URSS:[ЛИБРОКОМ], 2010.—149с.
3. Н. А. Газизуллин Гидродинамика потоков, создаваемых лопастной мешалкой // Вестник казанского технологического университета, №2, 2012, С.59-61.
4. А. С. Конаков, А. А. Назаров, С. И. ПоникаровМоделирование гидродинамики и нагрева реакционной смеси в экспериментальной установке вакуумного дегидрирования // Вестник казанского технологического университета, 2014, №7, С. 224-225.
Моделирование гидродинамики: Lattice Boltzmann Method

Моделирование извержения вулкана
с помощью Lattice Boltzmann Method. (с) Источник
В этой статье я расскажу о численном методе моделирования гидродинамики Lattice Boltzmann Method, LBM. На русском—метод решёточных уравнений Больцмана. Он превосходит другие известные методы (например, finite element method) в легкости распараллеливания, возможности моделирования многофазных потоков, моделировании потоков в пористых средах. Кроме того, вычислительный алгоритм содержит только простейшие арифметические операции. Метод весьма новый, первые коммерческие продукты на его основе стали появляться около 2010 года.
На хабре уже была серия статей по физике жидкости, и эта статья может быть ее логическим продолжением. Она написана с таким расчетом, чтоб как быть полезной людям, хорошо знающим гидродинамику и методы моделирования, так и понятной новичкам в этой области (например, с людям с образованием software engineer). Конечно, в связи с этим многие вещи будут излишне подробными для экспертов, а на некоторые не хватит места. Статья получилось достаточно большой, но мне не хотелось бы разбивать ее на несколько частей.
Зачем все это нужно? Точнее, в каких отраслях нужно моделировать гидродинамику:
- самолетостроение, ракетостроение, автомобилестроение (характеристики кузова, работа двигателя, сопла)
- промышленная химия (разделение веществ, химические реакторы)
- метеорология, геология (потоки жидкости сквозь пористые среды, песчаники, дамбы)
- другие инженерные отрасли (ветряные электростанции)
- медицина (потоки крови, лимфы)
Статья будет включать следующие разделы:
- Обзор физики — высокоуровневый обзор основных необходимых уравнений
- Основная идея—описание основного принципа алгоритма
- Технические детали—более подробное объяснение исходных уравнений, вывод вычислительной схемы
- Уравнение Навье-Стокса
- Уравнение Больцмана
- Дискретное уравнение Больцмана
- Иллюстрация вычислительной схемы
- Пространственные решетки
- Равновесные функции распределения
- Несжимаемость
- Вязкость и число Рейнольдса
- Еще раз, все вместе
- Разное
- Дополнения к алгоритму
- Подводные камни
- Существующие решения
- Что почитать
Обзор физики
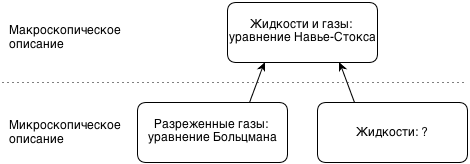
Гидро- и аэродинамика макроскопически описывается уравнением Навье-Стокса. Оно показывает, каким будет давление, плотность и скорость жидкости в каждой точке пространства в каждый момент времени—в зависимости от начальных и граничных условий и параметров среды.
С другой стороны, для разреженных газов справедливо уравнение Больцмана, которое описывает, как меняется плотность распределения частиц по скоростям в каждой точке пространства со временем. Если проинтегрировать распределение частиц по скоростям в данной точке, можно получить плотность и макроскопическую скорость в данной точке. Другими словами, макроскопически уравнение Больцмана эквивалентно уравнению Навье-Стокса.
Основная идея
Несмотря на то, что для плотных жидкостей уравнение Больцмана не применимо, если мы научимся его моделировать, то сможем моделировать и уравнение Навье-Стокса для этих жидкостей. То есть мы тем самым заменяем нижележащий уровень абстракций (микроскопическое уравнение для плотных жидкостей) физически неправильной реализацией (микроскопическое уравнение для разреженных газов), но так, что верхний уровень (макроскопическое уравнение Навье-Стокса) описывается верно.
Ситуация иллюстрируется картинкой ниже.
Вопросительный знак в ней символизирует тот факт, что я не знаю, какое уравненине описывает поведение плотных жидкостей на микроскопическом уровне. Иногда вместо «микроскопический» говорят «мезоскопический»—в том смысле, что микроскопическое описание—это описание поведения отдельных атомов и молекул, а уравнение Больцмана описывает потоки молекул.
Поскольку компьютер не умеет работать с непрерывными величинами, нам необходимо дискретизировать уравнение Больцмана: по времени, по пространственным координатам (получаем пространственные узлы для моделирования) и по возможным направлениям частиц в каждом пространственном узле. Направления выбираются специальным образом, и всегда указывают в некоторые соседние узлы.
Технические детали
В этом большом разделе находится более подробное объяснение исходных уравнений и вывод вычислительной схемы. Действительно важные уравнения должны быть понятны всем читателям с техническим образованием (требуются основы линейной алгебры, интегрального исчисления). Те уравнения, что непонятны, скорее всего, не важны (это те, где есть набла). Векторы обозначаются жирным шрифтом.
Уравнение Навье-Стокса
Вариант уравнения для макроскопической динамики несжимаемых жидкостей и газов выглядит так:
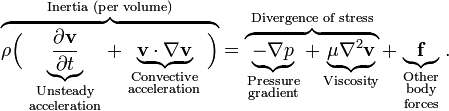
здесь v – скорость потока, ρ – плотность жидкости, p – давление в жидкости, f – внешние силы (например, гравитация).
Если вы не знаете, что такое перевернутые треугольнички и частные производные—не переживайте, они нам в дальнейшем не понадобятся, а вычислительный алгоритм содержит только простейшие арифметические операции.
Подробный вывод и физический смысл можно изучить на википедии и хабре, я же здесь приведу основную идею.
Мысленно выделим в жидкости некий малый объем и проследим за его движением. Ускорение, действующее на данный объем жидкости, определяется (i) давлениями слева, справа, сверху, снизу и т.п. (притом они частично компенсируют друг друга), (ii) действием внутренних сил трения в жидкости (iii) внешними силами. С другой стороны, ускорение можно выразить через разницу скоростей в начальный момент времени в начальной точке и в некоторый следующий момент времени в той новой точке, где будет находиться объем жидкости.
Если теперь подставить эти величины в уравнение Ньютона F = ma, после несложных преобразований мы получим уравнение выше. Слева находится ma, справа—F.
Уравнение Больцмана
Это уравнение оперирует функцией распределения плотности вероятности частиц по координатам и по скоростям, f(r, v,t). Величина f(x, y, z, vx, vy, vz, t) dx dy dz dvx dvy dvz показывает, какая доля частиц в момент времени t находится в кубе от x до x+dx, от y до y + dy, от z до z + dz со скоростями в диапазоне от vx до vx + dvx, от vy до vy + dvy, от vz до vz + dvz. Ее также можно записать в виде 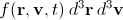
Эта функция обычно нормируется на массу газа в исследуемой системе, поэтому макроскопическая плотность газа в каждой точке определяется как сумма (интеграл) от плотности вероятности в данной точке по всем возможным значениям скорости, 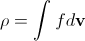
Аналогично, макроскопическую скорость можно определить через 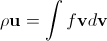
Основная идея для вывода уравнения похожа на вывод уравнения Навье-Стокса. Давайте мысленно выделим в данный момент времени в данном небольшом объеме пучок молекул, летящих в данном направлении (точнее, узком конусе направлений). Через небольшой промежуток времени dt они окажутся в соседней точке (благодаря наличию скорости), их скорость сама по себе изменится из-за ускорения молекул внешними силами. Кроме того, на этом отрезке пути некоторые молекулы столкнутся с другими, изменят свою скорость, и мы больше не сможем включать их в исходный пучок. С другой стороны, в результате столкновений молекул в том же объеме, летящих в другую сторону, некоторые из них приобретут нужное направление скорости, и мы добавим их в пучок.
Это можно записать в следующем виде: 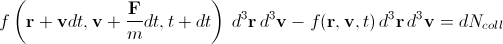
где F—внешняя сила, m—масса молекулы, dNcoll—изменение числа частиц в пучке за счет столкновений.
Как определяется в общем виде величина dNcoll, от читателя останется скрытым. Нам понадобится только ее стандартное приближение—Батнагара-Гросса-Крука (BGK). В этом приближении dNcoll равно 
где f eq —равновесная функция распределения, распределение Максвелла-Больцмана, а τ – так называемое время релаксации.
В итоге получаем 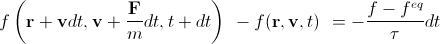
Заметим, что f eq зависит от макроскопических плотности и скорости в данной точке (то есть неявно от координаты и времени). Именно это уравнение нам понадобится в дальнейшем, но обычно его делят на dt и приводят к виду 
где набла с индексом v – это набла по переменным скорости.
Дискретное уравнение Больцмана
Чтоб получить возможность моделировать динамику непрерывного уравнения Больцмана на компьютере, нам необходимо его дискретизировать. Для этого сначала введем равномерную сетку пространственных координатам—шаг сетки пусть будет одинаковым по всем осям. Поведение жидкости мы будем определять именно в узлах сетки. Фактически, мы разрешаем молекулам находиться только в определенных пространственных узлах. Кроме того, мы должны дискретизировать время—мы будем определять состояние жидкости в равноотстоящие друг от друга моменты времени. Кроме того, мы позволим молекулам иметь только определенные значения скорости—такие, чтоб за шаг по времени они успевали перейти в какой-нибудь соседний узел. Эти разрешенные направления будут одинаковыми для всех пространственных узлов. Очевидно, что по диагональным направлениям скорости частиц будут больше, чем по недиагональным.
Интуитивно можно заключить, что при бесконечно малом шаге времени и шаге пространственной решетки эта дискретная система перейдет в обычное уравнение Больцмана, которое, в свою очередь, переходит к уравнению Навье-Стокса в макроскопическом пределе. Как ни странно, это не такой простой вопрос, и мы его пока отложим.
В дальнейшем изложении везде предполагается, что система единиц такова, что шаг решетки является единицей длины, а шаг по времени—единицей времени.
Для простоты ниже будем предполагать, что внешние силы отсутствуют. Мы пронумеруем разрешенные направления скорости от 1 до Q с индексом i. Если теперь массу частиц, пролетающих из данного узла в направлении i за шаг времени обозначить как fi, то уравнение (6) перейдет в 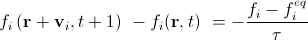
Здесь мы учли, что шаг по времени равен единице, и заменили все dt из (6) на единицу. fi eq обозначает дискретную равновесную плотность распределения, зависящую от макроскопических массы и скорости в данном узле. Мы не указали, из какого именно узла будем использовать fi eq —из r + vi t в момент времени t + 1 или из r в момент времени t. Для вычислительной схемы удобнее оказывается использовать узел r + vi t в момент времени t + 1. Тогда уравнение выше можно разложить на две составляющие, распространение (streaming step) и столкновение (collision step).
Streaming step: 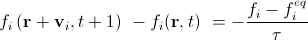
Collision step: 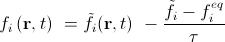
Здесь fi с тильдой обозначает массу частиц, пришедших в узел по направлению i, но еще не столкнувшихся с остальными пришедшими частицами. Streaming step иногда называют advection step.
Для дискретизированных направлений скорости масса и макроскопическая скорость в каждом узле будут рассчитываться как 
Здесь и далее мы пишем везде плотность вместо массы, поскольку при единичном пространственном шаге решетки на каждый узел приходится единичный объем, и масса и плотность совпадут по значению.
Мы покажем, что равновесные функции распределения зависят от массы в узлах и макроскопической скорости. Поэтому после streaming step необходимо пересчитать массы и скорости в каждом узле, пересчитать равновесные функции распределения, и потом совершать collision.
Таким образом, на каждом шаге вычислительной схемы необходимо «распространить» частицы, то есть переместить частицы, летевшие из узла r в направлении i в узел r + vi (проделать это для всех частиц и направлений). После этого необходимо пересчитать массы, скорости, равновесные функции распределения. Наконец, необходимо «столкнуть» частицы, прилетевшие в данный узел—то есть перераспределить частицы по направлениям.
Иллюстрация вычислительной схемы
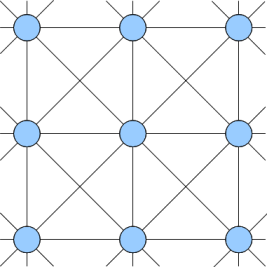
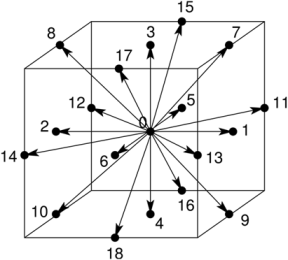
Проиллюстрируем вычислительную схему на примере двухмерной системы. Дискретизация на пространственные узлы и связи между ними (то есть разрешенные направления скорости) изображены на рисунке ниже. Пространственные узлы обозначены кружочками, связи между ними—тонкими линиями.
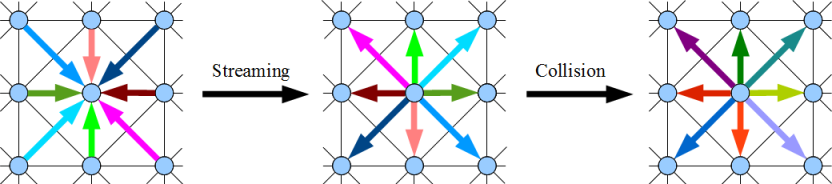
На следующем рисунке изображена одна итерация пары «streaming/collision». Цветные стрелки изображают потоки летящих молекул. Интенсивность цвета кодирует массу молекул, летящих в данном потоке, длина стрелок примерно соответствует пути, проходимом потоком за шаг по времени (лишь примерно, поскольку стрелки должны идти от центра узла до центра узла).
Пространственные решетки
В LBM под решеткой (lattice) понимается набор разрешенных векторов скорости (одинаковый для каждого пространственного узла). Это согласуется со стандартным математическим определением о решетке как о сущности, с помощью которой путем параллельных переносов можно получить все пространственную сетку (grid).
В LBM любая решетка должна содержать нулевой вектор из узла в себя самого—он описывает частицы, которые никуда не летят из данного узла. В LBM решетки обычно обозначаются аббревиатурой DnQm, где n—размерность пространства, m—число векторов в решетке. Например, D2Q9, D3Q19 и т.п.
В двумерном пространстве LBM решетка может состоять, например, из 5 векторов (2 вертикальных, 2 горизонтальных и нулевой вектор из узла в себя самого), а может из 9 векторов, как на иллюстрации выше (2 вертикальных, 2 горизонтальных, 4 диагональных, один нулевой). Это решетки D2Q5 и D2Q9, соответственно.
Очевидными факторами для выбора решеток являются: 1. точность моделирования (интуитивно понятно, что чем больше векторов в решетке, тем точнее моделирование) 2. вычислительные затраты (расчет на решетке D2Q5 будет быстрее расчета на D2Q9). Как ни странно, это не самые важные факторы. Самые важные факторы—это воспроизводимость уравнений Навье-Стокса и симметрия некоторых тензоров, построенных на векторах решетки.
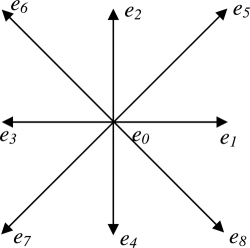
Обычно используются решетки D2Q9, D3Q15, D3Q19. Решетки D2Q9 и D3Q19 изображены ниже. Базисные вектора решетки обычно обозначаются как ei или ci (они совпадут со скоростями vi, введенными ранее при единичном шаге по времени). Ниже мы будем использовать обозначение ei.
Выпишем базисные вектора для D2Q9:
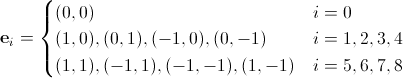
и для D3Q19:

Еще раз напомню, что мы везде предполагаем, что шаг по времени равен единице, поэтому vi = ei.
Равновесные функции распределения
В непрерывном случае равновесная функция распределения (распределение Максвелла-Больцмана) равна 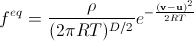
Здесь есть ранее не встречавшиеся величины: R—универсальная газовая постоянная, T—температура, D—размерность пространства, v—вектор скорости, плотность вероятности для которого мы и находим. Здесь молярная масса газа принимается равной единице (она для нас не важна—важна только макроскопическая плотность). Можно считать это изменением единицы массы в нашем моделировании. Кроме того, функция нормируется на локальную макроскопическую плотность, а не на единицу. Заметим также, что обычно от v не отнимают макроскопическую скорость газа u. Это происходит потому, что обычно распределение исследуют в случае неподвижного газа, нам же необходимо перейти в локальную инерционную систему отсчета, движущуюся с текущей скоростью газа в данной точке в данный момент времени, чтоб использовать распределение Максвелла-Больцмана. Вычитание u и является таким переходом.
Предположим, что в данной точке пространства распределение молекул по скорости оказалось равновесным. Это распределение зависит от макроскопической массы ρ и скорости u. С другой стороны, мы можем вычислить ρ и u по функции распределения (см. формулы (2) и (3)). Очевидно, это вычисление должно дать правильные ρ и u (то есть это в каком-то смысле дополнительное ограничение на функцию распределения): 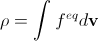
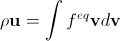
Такое же требование мы налагаем на вычисление плотности и скорости в дискретном случае: 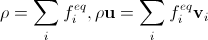
Основным требованием для дискретных равновесных функций распределения является воспроизводство уравнения Навье-Стокса в пределе бесконечно малых шага по времени и шага решетки. Это эквивалентно тому, что если при заданных ρ и u мы попытаемся их снова рассчитать по равновесным функциям распределения в непрерывном и дискретном случае, результаты совпадут (см. замечание выше о том, что в дискретном случае вместо плотности имеется в виду масса), т.е. 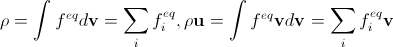
Для однозначного определения равновесной дискретной функции распределения нам необходимо будет также включить аналогичное требование равенства макроскопических тепловых энергий в данной точке, мы его опустим для краткости.
Если просуммировать по направлениям скорости уравнение (10) для collision step, то с учетом формулы (16) можно показать, что collision step не изменяет макроскопические массы и скорости молекул, находящихся в узле.
Оказывается, если просто подставить дискретные векторы скорости ei=vi из (11) и (12) в непрерывную равновесную функцию распределения (13), равенства (16) не будут выполняться.
Оказывается также, что мы можем заставить равенства (16) выполняться, если разложим распределение Максвелла-Больцмана (13) в ряд Тейлора до второго порядка макроскопической скорости. Это соответствует тому, что величина u/sqrt(RT) очень мала. Это ограничение всегда должно выполняться в процессе моделирования во всех узлах.
Но даже разложения в ряд Тейлора недостаточно. Мы также должны ввести в дискретизированные функции fi eq специально подобранные множители wi (детали вычислений можно найти в этой прекрасной статье—есть и бесплатная версия; конечно же, все окажется немного сложнее, чем в нашем поверхностном описании—на самом деле, расчет происходит через тензоры, вплоть до четвертого ранга, построенные на векторах решетки). Окончательно получим 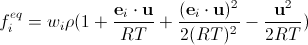
Здесь кроется подвох: мы везде предполагаем, что шаг решетки и времени являются единицами длины и времени, соответственно. Потому мы не можем взять значение R из СИ, а температура здесь не равна температуре моделируемой жидкости в Кельвинах.
Чтоб определить их значения, заметим следующее. Предположим, что в жидкости имеется возмущение—то есть в некоторых узлах есть избыточная масса. Эта масса начнет «растекаться» по пространству, притом в крайнем правом узле в области возмущения она будет двигаться в том числе и по направлению (1, 0, 0) в 3D или (1, 0) в 2D. За единицу времени молекулы вдоль этих направлений пройдут единицу длины, то есть их скорость будет равна единице. Это означает, что скорость звука как скорость распространения возмущений в нашей системе тоже равна единице. С другой стороны, скорость звука равна sqrt(γ R T / μ), где γ—это постоянная адиабаты, μ—молярная масса, которую мы приняли равной единице ранее. Постоянная адиабаты γ равна 1 + 2 / d, где d—число степеней свободы молекул. В идеальном газе оно равно размерности пространства. В нашем газе молекулы могут двигаться только вдоль прямых, соединяющих узлы, потому размерность равна не трем (или двум), а единице. То есть γ=3, а sqrt(3 R T) = 1.
Обычно в литературе по LBM под «скоростью звука» понимают величину 
Теперь, окончательно, 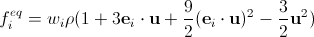
Выпишем значения коэффициентов wi для самых распространенных решеток.
Для D2Q9:
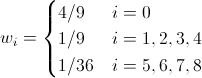
Для D3Q19:
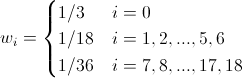
Несжимаемость
Ограничение на малую макроскопическую скорость жидкости теперь можно записать как 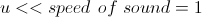
Напомним, что число Маха есть отношение характеристической скорости газа в системе к скорости звука. Тогда ограничение выше соответствует малым числам Маха или несжимаемой жидкости. Действительно, если скорость звука (скорость распространения возмущений плотности) велика, то любое возмущение плотности быстро распространится на всю систему, и плотность станет снова одинаковой. То есть сжать жидкость в какой-либо одной локальной области вам не удастся.
Хорошее максимальное значение для макроскопической скорости в узлах будет, например, 0.01.
Вязкость и число Рейнольдса
Кинематическая вязкость ν в LBM (как обычно, в единицах решетки) рассчитывается как 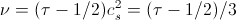
Здесь τ—время релаксации, введенное ранее в формуле (5), cs=1/sqrt(3)— «скорость звука», введенная в (18).
При моделировании гидродинамики без учета изменений температуры любая система с наперед заданной геометрией (например, труба с квадратным сечением) полностью описывается только одним безразмерным параметром—числом Рейнольдса, равным 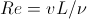
где v—характеристическая скорость в системе (например, скорость в центре трубы), L—характеристическая длина в системе (например, длина стороны квадрата сечения).
Для стандартных геометрий обычно известна связь между характеристической скоростью и внешней силой (которая обеспечивает поток). Поэтому для моделирования с заданным числом Рейнольдса необходимо
- выбрать характеристическую скорость v. Как мы выяснили, она должна быть намного меньше скорости звука. Например, 0.01.
- рассчитать необходимую внешнюю силу для такой скорости
- рассчитать вязкость по (23) так, чтоб получить нужное число Рейнольдса
- рассчитать время релаксации по (24) так, чтоб получить нужную вязкость
Если задача моделирования составлена в единицах СИ (мол, сторона квадрата сечения трубы 1м, давление на входе трубы X Паскалей, на выходе—Y Паскалей), то сначала надо найти безразмерное число Рейнольдса, и воспользоваться алгоритмом выше.
Еще раз, все вместе
Перед моделированием надо задать начальные макроскопические массы и скорости в каждом узле. Потом задать потоки масс в каждом разрешенном направлении ei в каждом узле (см. Подводные камни). Самый простой способ—указать потоки из равновесного распределения.
Для моделирования в цикле совершать
- streaming step по формуле (9)
- пересчет макроскопических масс и скоростей в каждом узле по формулам (11), пересчет равновесных потоков по всем направлениям по формуле (19)
- collision step по формуле (10)
Моделирование обычно происходит до тех пора, пока система не находится в стационарном состоянии. Стационарность можно проверять, например, через разницу макроскопических скоростей и масс в каждом узле между соседними шагами, максимальную среди всех узлов.
Разное
Дополнения к алгоритму
Мы не коснулись включения внешних сил в моделирование (например, гравитации). Они приведут к небольшой добавке в уравнение (9) для streaming step.
Мы также не коснулись граничных условий—на поверхности тел и на входе и выходе системы (например, если на входе трубы задано постоянное давление или поле скоростей). В LBM есть большая свобода в моделировании таких условий, поскольку метод формулируется на микроскопическом уровне (потоки молекул), а такие граничные условия—на макроскопической уровне. Существует множество способов задать граничные условия на микроскопическом уровне—и множество алгоритмов.
Граничные условия на границе твердых тел в гидродинамике обычно выбираются как no-slip boundary conditions (то есть когда скорость жидкости на поверхности тел равна нулю). Обычно они реализуются через bounce-back conditions (когда потоки молекул отражаются в обратном направлении при пересечении твердой стенки).Об этом можно почитать здесь, раздел 4.6.
Модель столкновений, которую мы представили, называется single relaxation time. Существуют более совершенные модели, например, multiple relaxation time (в частности, double relaxation time).
LBM также поддерживает многофазность (моделирование потока смеси жидкостей или газов с разными параметрами).
Наличие теплопроводности (то есть переноса тепла в системе, изменения температуры в разных точках системы и, как следствие, изменения параметров системы—например, плотности) также поддерживается LBM. Температура моделируется как отдельный «газ», тоже по алгоритму LBM, но скорость этого газа определяется скоростью основной жидкости. Говорят, что температура в этом смысле является passive scalar. Есть немало статей по моделированию через LBM явления Rayleigh–Benard convection.
Мы совершенно не коснулись вопросов эффективной реализации и параллелизации.
Подводные камни
Если вы моделируете систему с теплопроводностью, то она будет описываться двумя безразмерными величинами. В случае Rayleigh-Benard convection обычно выбирают число Прандтля и число Рэлея. Для того, чтобы воспроизвести эту систему в единицах решетки, недостаточно просто воспроизвести обе этих безразмерных величины, правильно задав внутренние параметры системы (характеристическая скорость, внешняя сила, теплопроводность). Дело в том, что между внутренними параметрами будут существовать скрытые зависимости. Подробнее можно почитать тут.
Как мы уже сказали, при выборе характеристической скорости в системе не забывайте о том, что число Маха должно быть много меньше единицы (формула (22)).
LBM может стать нестабильным в некоторых системах при высоких числах Рейнольдса (когда поток, тем не менее, все еще ламинарный).
В начале моделирования необходимо задать потоки молекул из каждого узла по всем разрешенным направлениям. Часто выбирают равновесное распределение потоков (формула (19)). Важно помнить, что равновесность не предполагает стационарность. То есть стационарные распределения при наличии градиентов скорости, внешней силы и т.п. отличаются от равновесных. Их расчет приведен здесь (формулы 12, 19, 20 по ссылке).
Существующие решения
Есть большой и очень зрелый open-source проект, целиком посвященный LBM—Palabos (PArallel LAttice BOLtzmann). У проекта есть и вики. Разработчики предоставляют платную консультацию по моделированию гидродинамики.
Здесь есть прекрасные обучающие примеры моделирования типичных систем на MATLAB. Например, Rayleigh–Benard convection (в наличии внешняя сила, теплопроводность, граничные условия, правильный перевод величин). Всего 160 строчек в MATLAB.
Есть множество коммерческих решений, например, это или это.
Подробный список коммерческих и некоммерческих пакетов по LBM можно найти на википедии.
Что почитать
Помимо всех ссылок, что есть в статье, можно порекомендовать эти списки статей и книг. В основном аналогичный список книг есть и на википедии.
Методы аппроксимации уравнений гидродинамики природных процессов
Большой круг рассматриваемых задач химической технологии, да и вообще, инженерной практики, тем или иным образом связаны с процессами гидродинамики. При всей своей распространенности вопросы гидродинамики имеют сложный характер, как в теоретическом, так и в реализационном аспекте.
Гидродинамические характеристики потоков в технологическом объекте можно определить экспериментально и теоретически. Не смотря на то, что данные экспериментальных исследований надежны и точны, проведение самих испытаний является дорогостоящей, трудоемкой и длительной операцией. Альтернативой является применение вычислительной гидродинамики (ВГД). Вычислительная гидродинамика это подраздел механики сплошных сред, включающий совокупность физических, математических и численных методов, предназначенных для вычисления характеристик потоковых процессов.
Преимуществами вычислительной гидродинамики перед экспериментальными исследованиями является полнота полученных данных, низкая стоимость, высокая скорость и др. Конечно, применение вычислительной гидродинамики не отменяет постановку самого эксперимента, однако ее применение позволяет значительно ускорить и удешевить достижение поставленной цели.
Актуальность темы. В странах СНГ практика использования вычислительной гидродинамики появилась сравнительно недавно и только в отраслях требующих сверхточных вычислений – авиация, аэрокосмическая отрасль. Это связано, прежде всего, с большой ее наукоемкостью. Не смотря на это, как уже отмечалось ранее, использование вычислительной гидродинамики при анализе характеристик потоков в технологических объектах, позволяет значительно снизить затраты и увеличить скорость при проектировании. Поэтому вопрос ее внедрение в проектно-расчетный процесс является чрезвычайно актуальным в условиях мировой экономической ситуации.
Цель работы – использование численных техник, реализованных в программных системах конечно-элементного анализа для получения характеристик технологических потоков в объекте химической технологии. Сравнение полученного численного решения с экспериментальными данными.
Вопросами вычислительной гидродинамики занимается доц. каф. «Промышленная теплоэнергетика» Пятышкин Георгий Георгиевич.
Системы конечно-элементного анализа использовали в своих работах для моделирования течения жидкости и газа в промышленных объектах магистры ДонНТУ: Болотин Е.О., Волошин В.В. Стеценко В.Ю. в своей работе использовала метод контрольного объема.
В Украине пакеты численного моделирования используются в основном проектно-конструкторскими институтами, реже – научно-исследовательскими.
В мире программные пакеты, основанные на методах вычислительной гидродинамики, активно используются как в инженерно-конструкторской, так и в научно-исследовательской деятельности.
Многие технологические процессы химической промышленности связаны с движением жидкостей, газов или паров, перемешиванием в жидких средах, а также с разделением неоднородных смесей путем отстаивания, фильтрования и центрифугирования. Скорость всех указанных физических процессов определяется законами гидромеханики.
Законы гидромеханики и их практические приложения изучаются в гидравлике, которая состоит из двух разделов: гидростатики и гидродинамики. Гидростатика рассматривает законы равновесия в состоянии покоя, а гидродинамика – законы движения жидкостей и газов.
Значение изучения гидравлики для инженера-химика не исчерпывается тем, что ее законы лежат в основе гидромеханических процессов. Гидродинамические закономерности часто в значительной степени определяют характер протекания процессов теплопередачи, массопередачи и химических реакционных процессов в промышленных аппаратах [1,2,3].
Основными уравнениями гидродинамики являются уравнения Навье-Стокса. Система состоит из уравнений движения и уравнений неразрывности.
В векторном виде для несжимаемой ньютоновской жидкости они записываются следующим образом:
 | (1) |
где η – динамическая вязкость, Па·с; ρ – плотность, кг/м 3 ; .jpg)
.jpg)
В гидродинамике выделяют два основных типа течения жидкостей – ламинарное и турбулентное. Особые трудности для изучения и моделирования вызывает именно турбулентное течение.
Турбулентность – название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средних значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов, а также линейных и нелинейных волн, струй. Турбулентность возникает, когда число Рейнольдса превышает некое критическое значение. Турбулентность может возникать и при нарушении сплошности среды, например, при кавитации (кипении). Мгновенные параметры среды становятся хаотичными. Моделирование турбулентности – одна из наиболее трудных и нерешённых проблем в гидродинамике и теоретической физике [4].
В настоящий момент создано большое количество разнообразных моделей для расчёта турбулентных течений. Они отличаются друг от друга сложностью решения и точностью описания течения.
Ниже перечислены модели по возрастанию сложности. Основная идея моделей сводится к предположению о существовании средней скорости потока и среднего отклонения от него: u = uср+ u’. После упрощения уравнений Навье-Стокса, в них помимо неизвестных средних скоростей появляются произведения средних отклонений u’iu’j. Различные модели по-разному их моделируют.
- Модель Буссинеска (Boussinesq). Уравнения Навье-Стокса преобразуется к виду, в котором добавлено влияние турбулентной вязкости.
- Модель Спаларта-Альмараса. В данной модели решается одно дополнительное уравнение переноса коэффициента турбулентной вязкости.
- k-ε модель. Уравнения движения преобразуется к виду, в котором добавлено влияние флуктуации средней скорости. В данной модели решается два дополнительных уравнения для транспорта кинетической энергии турбулентности и транспорта диссипации турбулентности.
- k-ω модель. Похожа на предыдущую, но вместо уравнения диссипации решается уравнение для скорости диссипации турбулентной энергии.
- Модель напряжений Рейнольдса. В рамках усреднённых по Рейнольдсу уравнений (RANS) решается семь дополнительных уравнений для транспорта напряжений Рейнольдса.
- Метод крупных вихрей (LES, Large Eddy Simulation). Занимает промежуточное положение между моделями, использующими осреднённые уравнения Рейнольдса и DNS. Решается для больших образований в жидкости. Влияние вихрей меньше, чем размеры ячейки расчётной сетки, заменяется эмпирическими моделями.
- Прямое численное моделирование (DNS, Direct Numerical Simulation). Дополнительных уравнений нет. Решаются нестационарные уравнения Навье-Стокса с очень мелким шагом по времени, на мелкой пространственной сетке.
В [5] рассматривается одна, из наиболее часто используемых и простых моделей турбулентности – RNG k-ε модель турбулентности.
RNG модель турбулентности (англ. renormalization group based k-ε model – k-ε модель основанная ренормализационной группе) получила в последнее время широкое распространение благодаря хорошему совпадению получаемых численных результатов с имеющимися экспериментальными данными, а также высокой скорости сходимости базового алгоритма. В этой модели параметры турбулентности вычисляются из уравнений:
где k – кинетическая энергия турбулентности, νt – турбулентная вязкость, ε – скорость диссипации турбулентности,
Эмпирические константы в приведенных уравнениях равны [5]:
Начальные и граничные условия. Для того чтобы решение системы (1) однозначно определяло распределения скоростей и давления, необходимо сформулировать начальные и граничные условия.
В нестационарных задачах, когда в уравнениях движения сохраняются члены с частными производными по времени, во всей области течения должны быть заданы начальные распределения компонент скорости жидкости, причем последние в начальный момент времени должны удовлетворять уравнению неразрывности. Начального распределения давления задавать не следует, так как уравнения не содержат производной давления по времени.
Область, в которой находится движущаяся реагирующая смесь, как правило, занимает не все пространство, а лишь его часть, ограниченную некоторыми поверхностями. В зависимости от того, принадлежит или не принадлежит области течения бесконечно удаленная точка, задача определения искомых функций называется соответственно внешней или внутренней задачей гидродинамики [6].
Вычислительная гидродинамика (ВГД) – это раздел науки, решающий проблему моделирования тепломассопереноса в различных технических и природных объектах. Основной задачей ВГД является численное решение уравнений Навье-Стокса, описывающих динамику жидкости. Дополнительно учитываются различные физико-химические эффекты: горение, турбулентность или потоки сквозь пористую среду.
ВГД как прикладная наука сформировалась в середине 20 века. Основным потребителем ее результатов была аэрокосмическая промышленность.
С развитием высокопроизводительных компьютеров, которые стали доступны по цене большому числу пользователей, в 70-х годах началось бурное развитие коммерческих программ вычислительной гидродинамики. В 80-х и начале 90-х годов эти программы устанавливаются на компьютеры класса «рабочие станции». В конце 90-х годов дешевые персональные компьютеры догнали по мощности рабочие станции, а основная операционная система, которая устанавливается на них — MS Windows — стала превосходить по уровню пользовательского интерфейса графические оболочки операционных систем рабочих станций. В это время появились программы в области ВГД, предназначенные для персональных компьютеров [7].
Численное решение задач, связанных не только с течением жидкости, но и с теплообменом и другими сопутствующими процессами, можно начинать, когда законы, управляющие этими процессами, выражены в математической форме, обычно в виде дифференциальных уравнений [8]. Как уже отмечалось ранее, течение жидкости описывается уравнениями Навье-Стокса. Они интересны тем, что содержат как линейные, так и нелинейные дифференциальные операторы, матрицы которых имеют нетривиальную форму и требуют специальных численных процедур при их реализации в глобальной системе алгебраических уравнений [9].
Основная идея численного решения заключается в аппроксимации дифференциальных уравнений поставленной задачи – построение дискретного аналога задачи. В результате, решение задачи сводится к решению систем линейных алгебраических уравнений.
Любое применение вычислительной гидродинамики состоит из последовательных этапов:
1. Подготовительный этап. На данном этапе формируется геометрия модели, формулируются необходимые физические условия, геометрия дискретизируется, задаются начальные и граничные условия дифференциальных уравнений;
2. Расчёт. На данном этапе численно решаются основные уравнения с точки зрения базовых физических параметров (скорость, давление, плотность, температура, энтальпия и т. д.);
3. Анализ. Результаты решения отображаются в виде графиков, таблиц, а также контурных, векторных схем.
Существуют различные методы решения системы дифференциальных уравнений:
— Метод конечных разностей;
— Метод конечных объемов;
— Метод конечных элементов;
— Метод сглаженных частиц;
— Метод с использованием функции распределения вероятности.
В настоящее время наибольшую распространенность получили метод конечных объемов и метод конечных элементов.
Метод конечных объемов. Одним из наиболее часто используемых в инженерных приложениях является метод контрольных объемов. Важным достоинством этого метода является выполнение как локальных, так и глобального законов сохранения. Выполнение таких законов чрезвычайно важно [9]. Основная идея метода контрольного объема легко понятна и поддается прямой физической интерпретации. Расчетную область разбивают на некоторое число непересекающихся контрольных объемов таким образом, что каждая узловая точка содержится в одном контрольном объеме. Дифференциальное уравнение интегрируют по каждому контрольному объему. Для вычисления интегралов используют кусочные профили, которые описывают изменение искомой функции между узловыми точками. В результате находят дискретный аналог дифференциального уравнения, в который входят значения искомой функции в нескольких узловых точках.
Полученный подобным образом дискретный аналог выражает закон сохранения искомой функции для конечного контрольного объема точно так же, как дифференциальное уравнение выражает закон сохранения для бесконечно малого контрольного объема. Одним из важных свойств метода контрольного объема является то, что в нем заложено точное интегральное сохранение таких величин, как масса, количество движения и энергия на любой группе контрольных объемов и, следовательно, на всей расчетной области. Это свойство проявляется при любом числе узловых точек, а не только в предельном случае очень большого их числа. Таким образом, даже решение на грубой сетке удовлетворяет точным интегральным балансам.
Метод конечных элементов. В методе конечных элементов расчетная область разбивается на элементы, такие, как треугольники и четырехугольники. Обычно дискретные аналоги получаются с помощью вариационного принципа, если он существует, или с помощью метода Галеркина, являющегося частным случаем метода взвешенных невязок. Для описания изменения зависимой переменной на элементе используются предположения о характере функции формы или профиля.
С этой точки зрения метод конечных элементов не следует рассматривать как отличающийся в принципе от конечно-разностного метода. Его дополнительные возможности обусловлены только тем, что при этом методе можно использовать нерегулярную сетку. Хотя в настоящее время уже существует метод контрольного объема на неструктурированной сетке [8].
В настоящее время существует программное обеспечение, реализующее методы контрольного объема и конечных элементов. Наиболее распространёнными вычислительными системами такого рода являются: ANSYS, COMSOL Multiphysics, CFdesign, FlowVision, Star-CD и др.
Несмотря на различия, эти программы имеют похожий принцип работы.
Для создания и расчета любой задачи рекомендуется следующая последовательность действий:
- Выбрать размерность модели, определить физический раздел и определить стационарный или нестационарный анализ процесса.
- Определить рабочую область и задать геометрию.
- Задать исходные данные, зависимости переменных от координат и времени.
- Указать физические свойства и начальные условия.
- Указать граничные условия (ГУ).
- Задать параметры и построить сетку конечных элементов.
- Определить параметры блока решения и запустить расчет.
- Настроить режим отображения.
- Получить результаты [10].
Ниже, на рисунке 1 и рисунке 2, представлено распределение поля скоростей и поля давлений полученное методом конечных элементов при моделировании сужающего устройства – диафрагмы. Основные характеристики диафрагмы:
| Технологическое вещество | вода; |
| Температура технологического вещества | 20°С; |
| Диаметр трубы | D = 0,03 м; |
| Диаметр отверстия диафрагмы | d0 = 0,024 м; |
| Толщина диафрагмы | δ = 0,002 м; |
| Потеря давления на участке трубопровода с диафрагмой (при средней скорости потока 1,4 м/с) | 900 Па. |
Решаемые уравнения: стандартная k-ε модель турбулентности.
Граничные условия:
| — на входе: | Параболический профиль Пуазейля с максимумом 1 м/с; Интенсивность турбулентности – 0.05; Масштаб турбулентности – 0.07D (D – диаметр поперечного сечения) |
| — на выходе: | Давление – 101325 Па |
| — на стенке: | Логарифмический закон. Расстояние до ближайшей стенки – h/2 (h – характерный размер элемента сетки) |
Решение проведено на сетке состоящей из 7039 треугольников и 4019 вершин.
 |  |
| Рис. 1. Поле скоростей | Рис. 2. Поле относительных давлений |
Это же сужающее устройство, смоделировано в нестационарных условиях используя метод контрольного объема (рис. 3 и рис. 4). Ниже представлена анимация осцилляций скорости и давления.
 |  |
| Рис. 3. Осцилляции скорости (30 кадров, 7 повторений, задержка 40 мс) | Рис. 4. Осцилляции давлений (30 кадров, 7 повторений, задержка 30 мс) |
Проведение эксперимента заключается в создании опытной модели, постановку эксперимента с регистрацией основных параметров. Далее, постановка численного эксперимента. Сравнение полученных данных с натуральными испытаниями. В случае адекватности математической модели, проведение оптимизации с применением численного эксперимента. В заключении, постановка натурального эксперимента с оптимизированными параметрами.
Следует отметить, что на данный момент этот этап магистерской работы находится на стадии разработки.
Вычислительная гидродинамика является универсальным средством анализа процессов течения жидкости и газа, а так же теплообменных и массообменных процессов. Достижение целей, поставленных в магистерской работе, позволит в очередной раз подтвердить адекватность численных экспериментов в области гидродинамики. Изучить гидродинамические особенности исследуемого объекта и оптимизировать его параметры.
- Касаткин А.Г. Основные процессы и аппараты химической технологии. – М., 1970. – 784 с.
- Дытнерский Ю.И. Процессы и аппараты химической технологии: Учебник для вузов. Изд. 2-е. В 2-х кн.: Часть 1. Теоретические основы процессов химической технологии. Гидромеханические и тепловые процессы и аппараты. – М.: Химия,1995. – 400 с.: ил.
- Гельперин Н.И. Основные процессы и аппараты химической технологии. – М.: Химия, 1981. – 812 с.: ил.
- Ошовский В.В., Охрименко Д.И., Сысоев А.Ю. Использование компьютерных систем конечно-элементного анализа для моделирования гидродинамических процессов // Наукові праці ДонНТУ. Cepія: Хімія i хімічна технологія, 2010. – Вип. 15(163). – С. 163-173.
- Черный С.Г., Шашкин П.А., Грязин Ю.А. Численное моделирование пространственных турбулентных течений несжимаемой жидкости на основе k-ε моделей. // Вычислительные технологии, 1999. – Том 4, №2. – С. 74-94.
- Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика: Справочное пособие. – М.: Квантум, 1996. – 336 с.
- Система моделирования движения жидкости и газа FlowVision. Версия 2.05.04. Руководство пользователя. – М., 1999-2008. – 310 с.
- Патанкар С. Численные методы решения задач теплообмена и динамики жидкости: Пер. с. англ. – М.: Энергоатомиздат, 1984. – 152 с., ил.
- Фирсов Д.К. Метод контрольного объема на неструктурированной сетке в вычислительной механике. Уч. пособие: – Томск, 2007. – 72 с.
- Егоров В.И. Применение ЭВМ для решения задач теплопроводности. Учебное пособие. – СПб: СПб ГУ ИТМО, 2006. – 77 с.
http://habr.com/ru/post/190552/
http://masters.donntu.org/2010/feht/okhrimenko/diss/index.htm