Математическое моделирование задач искажения магнитных полей статики и квазистатики электромагнетизма методом поверхностных интегральных уравнений теории потенциала Чегис, Инна Александровна
Данная диссертационная работа должна поступить в библиотеки в ближайшее время
Уведомить о поступлении
480 руб. | 150 грн. | 7,5 долл. ‘, MOUSEOFF, FGCOLOR, ‘#FFFFCC’,BGCOLOR, ‘#393939’);» onMouseOut=»return nd();»> Диссертация, — 480 руб., доставка 1-3 часа, с 10-19 (Московское время), кроме воскресенья
Автореферат — бесплатно , доставка 10 минут , круглосуточно, без выходных и праздников
Чегис, Инна Александровна. Математическое моделирование задач искажения магнитных полей статики и квазистатики электромагнетизма методом поверхностных интегральных уравнений теории потенциала : автореферат дис. . доктора физико-математических наук : 05.13.18 / Моск. гос. ин-т радиотехники, электроники и автоматики.- Москва, 2004.- 36 с.: ил. РГБ ОД, 9 04-7/1998-5
Введение к работе
Актуальность темы. В настоящее время поверхностные интегральные уравнения составили фундамент современной теории акустического и электромагнитного рассеяния (дифракции), о чем убедительно свидетельствует монография D-Колтона и R.Kpecca «Методы интегральных уравнений в теории рассеяния» ‘.
Классические результаты решения краевых задач для уравнения Лапласа, полученные сведением их к поверхностным интегральным уравнениям 2 , 3 были перенесены сначала на случай скалярного уравнения Гельмгольца 4 , 5 , а затем на решение внутренних и внешних краевых задач для векторного уравнения Гельмгольца и уравнений Максвелла. Все это составило основу современной теории электромагнитного рассеяния. Подробная библиография по этой тематике имеется в ‘.
В данной работе рассматривается другой важный класс задач прикладного электромагнетизма, задач, касающихся искажения внешнего магнитного поля Щ(х,і) при помещении в него проводящего тела V» В этих задачах решающую роль играют условия сопряжения электромагнитных полей на границе раздела сред, а также предположения об асимптотическом поведении решений уравнений Максвелла на бесконечности. В отличие от хорошо известных краевых задан для уравнений Максвелла (см.,например, ‘) этот весьма широкий класс задач прикладного магнетизма естественно назвать задачами с условиями сопряжения для уравнений Максвелла.
В настоящее время задачи этого класса решаются методом конечных элементов как существенно 3-мерные и во всём пространстве. Совместное совершенствование компьютерных технологий, алгоритмов и методов программирования позволяет расширять круг задач, поддающихся такому численному решению и в результате компьютерные расчеты магнитных полей оформились в мощную ветвь компьютерной индустрии, объединяющей коллективы научных работников и инженеров по
1 Колтон Д., Кресс Р. Методы интегральных уравнений в теории рассеяния. Москва.: Мир, 1987, 311 с.
»Ляпунов A.M. Sur certaines questions qui se rattachent aux probleme de Dirichlet. Собрание сочинении, Москва, 1954, Т. 1.
э Гюнтер Н.М. Теория потенциала и ео применение к основным задачам математической физики. М.-Л.: Гостехиздат, 1953, -116 с.
4 Векуа И.Н. Метагармонические функции. //Труды Тбилисского Математического ин-та. 1943,12, с. 105-174.
‘Купрадзе В.Д. Граничные задачи теории колебаний и интегральные уравнения. М.-Л.: Гостехиздат, 1950, 2в0 с.
М>С НАЦИОНАЛЬНАЯ БИБЛИОТЕКА
всему миру. Многочисленные международные конференции по этой тематике такие, как COMPUMAG, CEFC, ISEM и многие другие, существующие десятки лет, свидетельствуют о большой практической значимости этих задач и о постоянных поисках новых решений (см., например, 6 , 7 , 8 ).
В нашей стране многоплановое изучение свойств решений уравнений Максвелла проводилось рядом крупных учёных школы академика А.Н.Тихонова (см., например,’, 10 , «, 12 , 13 и др., а также 14 , 15 и др.).
В конце 80-х годов появился новый Т’— метод для нахождения электрического векторного потенциала в области V через интегро- дифференциальное уравнение по области V и ее границе, т.е. была сделана попытка решить задачу распределения вихревых токов как внутреннюю задачу и это обстоятельство, как отмечают сами авторы, является главным преимуществом, предлагаемого ими метода, 1б .
Таким образом, актуальной проблемой в решении задач с условиями сопряжения на границе ограниченной области V, которые решаются в настоящее время, в основном, методом конечных элементов во всём пространстве, является получение алгоритмов сведения этих задач к задачам с краевыми условиями на границе области V, а такие задачи, как известно, сводятся к поверхностным интегральным уравнениям теории потенциала.
Постановки задач.
Введем обозначения. Пусть V область в R 3 и V— дополнение к V,
Roger D., Eastham J. A formulation for low frequency eddy current solutions. //IEEE Trans, on Magnetics. 1983,19, N56, pp. 2443-2448.
7 Biddlecombe C, Heighway E., Simlrin J.f Trowbndge С Method for eddy current computations in three dimentions.//IEEETrans, on Magnetics. 1982, 18, №2, pp. 492-497.
«Biro O., Preis K. Finite element analysis of 3-d Eddy Currents. //IEEE Trans, on Magnetics, 1990. 26, №2, pp. 418-423.
*Ильинский A.C., Кравцов В В., Свешников АГ. Математические модели электодинамики. М.:Высшая школа, 1991,223 с.
I «Тихонов А.Н., Ильинский А. С, Свешников АГ. Математические модели излучаюших систем. //Сб.
Вычисл.методы и программирирование.Изд-во МГУ, 1980, вып.32, с. 82-108.
II Тихонов А,Н. К математическому обоснованию электромагнитного зондирования.// ЖВМ и МФ,
1Э65.Т.5, №3,с.545-547.
|2 Прилепко А.И., Орловский Д.Г Об определении параметра эволюционного уравнения и обратных задачах математической физики 3//Дифференциальные уравнения, 1987, т.23, №8, с. 1343-1353.
13 Худак НЖ О локальной структуре одного класса решений однородной системы уравнений Максвелла. // ДАН СССР, 1985, т.282, № 1, с. 61-65.
14 Дякин В.В., Раевский В.Я. К исследованию системы интегродифференциальных уравнений электродинамики с постоянными параметрами сред. // ЖВМ и МФ, 2001, т.41, №9, с. 1416-1421.
15 Самохин А.Б. Интегральные уравнения и итерационные методы в электромагнитном рассеянии. М.: Радио и связь, 1998, 160 с.
le Miya К., Ha&hizume Н. Application of T-method to A.C.Problem based on Boundary Element Method. //IEEE Trans, on Maenetics, 1988, 24, № 1, pp. 134-137.
V\ = R 3 \ V. Относительно области V предполагаем, что она односвязна и ограничена, а поверхность 5 = dV принадлежит классу гладкости С 2
Будем полагать, что магнитная проницаемость в области V постоянна и равна /і, что токами смещения по сравнению с токами проводимости можно пренебречь (см., например, 18 раздел «квазистационарное электромагнитное поле») и что электрические свойства области V можно характеризовать проводимостью а. В области Vj будем считать, что магнитная проницаемость также постоянна и равна ц\ ф /х, а о\ — 0.
Система уравнений Максвелла для квазистационарного поля , в случае гармонической зависимости от времени (как е
‘ ші ) электрических и магнитных полей, может быть записана в виде:
где J(x) = crE(x), igV,- вихревой ток.
На границе S раздела сред должны быть выполнены следующие условия сопряжения электрических и магнитных полей (см., например, 5 ):
u #i(e) — 0 при |x| -+ 00. (6)
Определение 1. Задачей А назовём решение системы (1), (2) при условиях(3)-(5) и (6).
Определение 1*. Задачей А* назовём решение системы (1), (2) при условиях(3)-(5) и (6*), где условие (6*) означает, что:
В работах [1,3-6] задача А распределения вихревых токов решалась при дополнительном предположении, что магнитное поле в среде V и соответствующий вихревой ток связаны условием, отражающим закон Био-Савара:
17 Эти ограничения на область V и ее границу 5 будут считаться выполненными далее всюду в данной работе.
«Ландау Л.Д., Лифшиц Е.М.Электродинамика сплошных сред (теоретическая физика Т. 8). Москва.: Наука, 1982, 620 с.
H(x) = Но(х) + J \.)<х), У,Ф0(х, у)) &VU, х Є V, (7)
где Фо(х, у) — l/AnrXIJ— фундаментальное решение уравнения Лапласа.
В монографии 18 имеются формулы точного решения задачи А* для шара Va и внешнего поля Но = Const ф 0.
Стоит отметить различие в интерпретации условий на бесконечности (6) и (6*). В первом случае источники, порождающие внешнее поле Ho(x)e
lu,t расположены в конечной части пространства К 3 , а во втором случае тело V помещается в неограниченный соленоид.
В режиме статики хорошо известной задачей искажения внешнего поля Hq(x) при внесении в него проводящего тела V, является задача нахождения размагничивающего поля H,t(x), х R 3 \S, и тесно связанная с ней задача распределения намагниченности М(х), х Є V.
Определение 2. Задачей В назовем задачу нахождения размагничивающего поля Hd(x), гармонического в областях V , Vi, непрерывного вплоть до границы S = dV, и такого, что для полей
H(x) = H0(x) + Hd(x),x&V, (8)
Hi(x) = Я0(х) + Hd
выполнено условие сопряжения (3) на границе раздела сред.
Определение 3. Задачей С назовем задачу нахождения распределения намагниченности М(х), х Є V, такого поля, которое компенсирует в области V внешнее поле Но<х) с помощью оператора электромагнитостатики:
Щ(х) = 4ttV f(M, УуФ0(х, у)) dVs, xeV. (10)
Целью настоящей работы является изучение свойств решений задач А, В, С, выявление связей этих задач с известными краевыми задачами для уравнений Максвелла и гармонических функций и получение на этом пути поверхностных интегральных уравнений для их решения.
Научная новизна заключается в следующем:
1) предложен новый метод решения задач А, В, С, который сводит их к решению поверхностных интегральных уравнений теории потенциала;
в рамках нового метода неизвестное электромагнитное поле не отыскивается во всем 3-х мерном пространстве, а находится плотность потенциала поля на замкнутой ограниченной поверхности с помощью решения двумерного интегрального уравнения. При таком подходе, во-первых, размерность носителей информации понижается на единицу и, во-вторых, исчезает бесконечная протяженность этих носителей. Оба указанных обстоятельства самым существенным образом позволяют упростить алгоритмы численного решения всех трех сформулированных выше задач А, В, С ;
для обоснования предложенного метода решения задачи. А доказана теорема (теорема 2.3.1) [5,6] о расщеплении уравнения (1) на уравнения, действующие в двух ортогональных подпространствах Вейля 19 , 20 . Теорема 2.3.1 позволила с одной стороны свести задачу А к краевой задаче для системы уравнений Максвелла и с другой стороны способствовала выяснению механизма действия условий сопряжения (3), (4);
доказаны теоремы (теоремы 3.2.1 и 3.3.1), указывающие точные условия существования и единственности решения системы уравнений Максвелла для задачи А в пространстве функций определенной гладкости [1|;
построен алгоритм численного решения задач В, С, основанный на решении внутренней задачи Неймана с помощью потенциала простого слоя [2]. Для отыскания плотности потенциала простого слоя предложен алгоритм, опирающийся на теорему об однозначной разрешимости пары уравнений Фредгольма второго рода в гильбертовом пространстве 2(6), S = dV, в случае, когда число Рисса задачи равно единице (теорема 5.2.1) [26];
Обоснование алгоритма решения задачи А* в случае произвольной геометрии области V потребовло введения нового понятия сопряжения гармонических полей (см. (24)) на границе раздела сред и доказательства теоремы 1.6.1 об общих спектральных свойствах трех известных интегральных операторов: оператора электромагнитостатики
интегральных операторов граничных задач Неймана
«Вейль Г. Метод ортогональной проекции в теории потенциала. Избр. тр. (Матем. и теор. физ.). Москва.: Наука, 1984,510 с
«Быховский Э.Б., Смирнов Н.В. Об ортогональном разложении пространства вектор-функции квад-ратичносуммируемых по данной области и операторах векторного анализа. //Тр. МИЛН СССР. М., I960, Т. 59, с. 5-36.
(K’0g)<X)=2jg(y)^0(x!y)dSl„ x Є S, (12)
и Максвелла при к =0
(Л/0с)(г) = 2 y[«(s), rotx У))) dSy, x&S (13)
[3] (см. также’, стр. 72 и 74).
Теорема 1.6.1 содержит в себе в качестве частного случая известный ранее результат об общих спектральных свойствах операторов (11) и (12), полученный в работе 21 .
Достоверность и обоснованность результатов исследований подтверждаются:
надежностью применяемого в работе и апробированного ранее, в работах других авторов, математического аппарата (ортогонального разложения Вейля, спектральных свойств операторов граничных задач, классических теорем о предельных значениях потенциалов, различных свойств интегральных уравнений и др.),
результатами, полученными другими авторами 21 , которые следуют как частный случай из теоремы 1.6.1,
результатами применения построенных численных алгоритмов для расчета плотности магнитного заряда (нормальной компоненты намаг-ниченнсти), которые согласуются с известными экспериментальными данными 22 ,
результатами теоретического и экспериметального характера других авторов по расчетам размагничивающих факторов эллипсоидов 23 . Эти результаты являются частными случаями применеия предложенного в диссертации алгоритма решения задачи С для эллипсоида и поля Hq(x) = Но, направленного вдоль одной из осей симметрии этого эллипсоида.
Практическая значимость. Представленная работа, имея теоретический характер, посвящена математическому моделированию электромагнитных полей и обоснованию алгоритмов решения практически
21 Дякин В.В., Раевский В.Я. Исследование одного уравнения электрофизики. //ЖВМ и МФ. 1990, 30, №2, с. 291-297.
22 Кринчик Г.С, Чепурова Е.Е., Шаматов У.Н., Раев В.К., Андреев А.К. Исследование распределения намагниченности в малых ферромагнитных элементах.//ФТТ, 1976, 18, № 12, с. 3581-3584.
«Муратов Р.З. Потенциалы эллипсоида. М.: Атомиздат, 1976, 200 с.
важных задач А, В, С.
Изучению различных аспектов решения задач А, В, С отводится видное место на всех международных конференциях по компьютерным расчетам магнитных полей COMPUMAG, CEFC, ISEM и др.. В настоящее время задачи А,В решаются, в основном, методом конечных элементов как существенно 3-х мерные задачи во всем пространстве. Предлагаемые автором алгоритмы открывают иные возможности для математического и численного моделирования устройств, содержащих проводящие элементы, которые влияют на внешнее магнитное поле или специально его преобразуют. К таким устройствам относятся, например, магнитные линзы, всевозможные датчики, в частности датчики, обнаруживающие скрытые дефекты и т.д..
Задача С является типичным примером некорректно поставленной задачи. Известно, что приближенное решение таких задач выделилось в самостоятельную ветвь вычислительной математики после основополагающих результатов А.Н. Тихонова, В.К.Иванова, М.М. Лаврентьева. Существенное развитие методы решения некорректных задач получили в работах А.Б. Бакушинского, А.С.Ильинского, А.И. Прилепко, АГ. Свешникова, АГ. Яголы, и др. авторов. Задача С могла бы решаться одним из методов, разработанных в этой области вычислительной математики, однако, специфика оператора (11), использование спектральных свойств этого оператора на подпространствах Вейля позволили свести решение задачи С к решению такого же интегрального уравнения (см. (17), (18)), как и в случае задачи В и использовать, следовательно, тот же численный алгоритм.
На защиту выносятся следующие результаты:
Об общих спектральных свойствах оператора электромагнитостатики (11) и интегральных операторов граничных задаче Неймана (12) и Максвелла (к = 0) (13) (Теорема 1.6.1).
О расщеплении системы уравнений Максвелла (1) для задачи А распределения вихревого тока J(x, і), принадлежащего гёльдерову пространству векторных полей
на уравнения, действующие в подпространствах Вейля 20 , и о представлении граничных значений ротора вихревого тока через плотности гармонических потенциалов простого и двойного слоя (Теорема 2.3.1).
3. О представлении решения системы интегральных уравнений с
гиперсингулярным ядром для плотностей гармонических потенциалов простого и двойного слоя (Теорема 2.5.1).
О точных формулах для граничных значений ротора вихревого тока через известный гармонический потенциал внешнего поля (Теорема 2.6.1).
Об интегральном представлении тока J(x) в области V через векторный потенциал вида
А(х) = j’ a
и а(х) — касательное векторное поле на 5 = dV, являющееся решением интегрального уравнения внешней краевой задачи для уравнений Максвелла:
а(х)+ 2 j[n(x),rotxa
а<х)-2 j
О существовании и единственности решения задачи А в гельде-ровом пространстве вектор-функций (14).
О представлении размагничивающего поля Hd(x), х Є R 3 \ S, (задача В) в виде градиента гармонического потенциала простого слоя с плотностью і( ж )>
удовлетворяющей интегральному уравнению
Vl(x) + <КУрд<х) = 2ф), (18)
где v?i(x) ортогональна единице на поверхности S и свободный член уравнения (18) является решением уравнения (17) (Теорема 4.3.1).
9. Алгоритм численного решения уравнения (17) в подпространстве
функций ортогональных единице на поверхности 5 (теорема 5.3.1).
Апробация и публикации. По тематике данной работы было сделано в общей сложности более 50 докладов.
Результаты диссертации регулярно докладывались на семинаре по вычислительным методам математической физики под руководством проф. АГ. Свешникова, проф. АС. Ильинского (физический факультет МГУ);
ряд докладов был сделан на семинаре по дифференциальным уравнениям в частных производных под руководством проф. В.П. Михайлова и др. (Математический институт РАН им. В.АСтеклова),
на семинаре под руководством проф. АИ. Прилепко (механико- математический факультет МГУ),
на семинаре под руководством акад. РАН, проф. В.А Ильина, чл.-корр. РАН, проф. АВ. Бицадзе, акад.РАН, проф. Е.И. Моисеева, проф. ААДезина (ВМК МГУ) (мой последний доклад на этом семинаре был сделан в марте 2003 года),
на семинаре под руководством проф.АБ.Бакушинского, проф.А.В.Тихо-нравова, проф. АГ. Яголы (Научно-исследовательский Вычислительный Центр МГУ) и др., а также на международных конференциях:
на VII Международной конференции COMPUMAG по компьютерным расчетам электромагнитных полей (Токио, Япония, 1989 г.),
на III Международном TEAM Workshop (Сорренто, Италия, 1991 г.),
on I Japan-CIS Joint Seminar on Electromagnetomechanics in Structures (Токио, Япония, 1992 г.),
на IV Международном симпозиуме ISEM по нелинейным явлениям в электромагнитных полях (Нагойя, Япония, 1992 г.),
on X International Symposium on Theoretical Electrical Engineering (Magdeburg, Germany, 1999),
на Международной конференции посвященной, 100-летию со дня рождения акад. М.А Лаврентьева (Киев, 2000г.),
on International Petrovskii Centenery Conference (Moscow, 2001),
First SIAM-EMS Conference «Applied Mathematics in our Changing World» (Berlin, Germany, 2001),
на V International Congress on Mathematicical Modeling VTCMM (Dubna, Russia, 2002),
on 3 Japanese-Mediterranean Workshop on Applied Electromagnetic Engineering . (Athens, Greece, 2003) и др..
Результаты диссертационной работы докладывались регулярно, начиная с 1982 г., на конференциях, проводимых в рамках Воронежских зимних (весенних) математических школ, организованных проф. С.Г. Крейном и проводимых в настоящее время проф. Ю.В. Покорным.
Основное содержание диссертации изложено в 30 печатных работах, список которых приведен в конце автореферата. Роль соавторов заключалась в разработке программ для компьютерных расчетов, получении численных результатов, а также в постановке и проведении экспериментов.
Структура и объем диссертации. Диссертация состоит из Введения, пяти глав, заключения, приложений и списка цитируемой литературы, содержащего 86 наименований. Полный объем диссертации 174 страницы.
Методы интегральных уравнений в теории рассеяния
В сферически-симметричном поле орбитальный момент частицы сохраняется. Применительно к задаче рассеяния это означает, что если представить падающий поток частиц как совокупность парциальных волн , соответствующих определенным значениям орбитального момента частицы, то каждая такая волна рассеивается на силовом центре независимо от других парциальных волн. С математической точки зрения это создает упрощение задачи, поскольку, решая волновое уравнение для каждой парциальной волны в отдельности, легко разделить переменные волновой функции и, в отличие от общего случая (1.4) или (1.9), свести дело к одномерным дифференциальным или интегральным уравнениям. С физической точки зрения важнейшим новым для нас аспектом при решении задачи рассеяния методом парциальных волн является вопрос о том, как интерферируют между собой разные парциальные волны, попадая в детектор рассеянных частиц. Рассмотрев взаимное поведение парциальных волн на больших расстояниях от рассеивающего центра, мы увидим, что вклад каждой из них в амплитуду рассеяния (а следовательно, в дифференциальное и полное сечения рассеяния) определяется всего лишь одним вещественным параметром − фазой рассеяния . Величина и энергическая зависимость фаз рассеяния определяются видом потенциальной энергии V(r).
Перейдем к последовательному изложению метода парциальных волн.
Из симметрийных соображений вполне ясно, что в случае рассеяния частицы сферически-симметричным потенциалом амплитуда рассеяния /(k,k‘) зависит лишь от модуля импульса
k = |k| = |k‘| (т. е. от энергии частицы Е) и от угла Э между векторами k и k‘ − угла рассеяния . Волновая функция задачи рассеяния 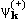
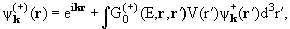 | (3.1) |
где, в отличие от (1.32), вместо V(r‘) стоит V(r’) и поэтому она тоже зависит лишь от r и угла θr между k и r, но не зависит от азимутального угла. Представим 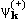
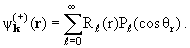 | (3.2) |
Функции Rℓ(r) будем называть радиальными функциями задачи рассеяния . Они, конечно, удовлетворяют тому же дифференциальному уравнению − радиальному уравнению Шредингера , что и радиальные волновые функции в задаче о связанных состояниях частицы:
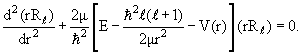 | (3.3) |
Однако, имея дело с задачей рассеяния, где более тонко стоит вопрос о дополнительных условиях к решению волнового уравнения, удобно наряду с дифференциальным уравнением (3.3) построить также и интегральное уравнение для функции R^(r), соответствующее интегральному уравнению (3.1).
Для этого подставим (3.2) в (3.1), разложим по парциальным волнам плоскую волну [1, с. 271]:
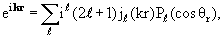 | (3.4) |
где jℓ(kr) − сферическая функция Бесселя, и, умножив правую и левую части уравнения на Pℓ(cosθr), воспользуемся свойством ортонормированности полиномов Лежандра:
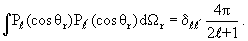 | (3.5) |
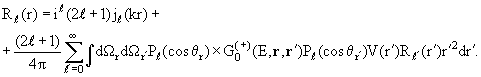 | (3.6) |
Воспользуемся вьфажением (1.21) для функции Грина, а также известным в теории специальных функций разложением [3]:
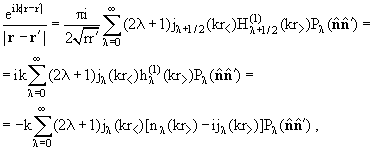 | (3.7) |
где r − большее из значений r и r‘, 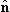
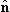
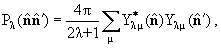 | (3.8) |
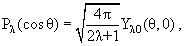 | (3.9) |
получаем интегральное уравнение для радиальных функций Rℓ(r) в окончательном виде:
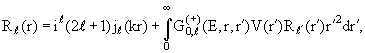 | (3.10) |
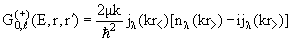 | (3.11) |
функция Грина для ℓ-й парциальной волны свободной частицы.
Рассмотрим асимптотику радиальных функций Rℓ(r) при больших r. Для этого нам понадобятся асимптотические выражения сферических функций Бесселя и Неймана, входящих в (3.10) и
(3.11) [1, с. 269]:
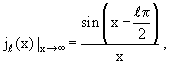 | (3-12) |
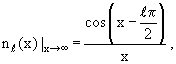 | (3-13) |
Подставляя их в (3.11), получаем
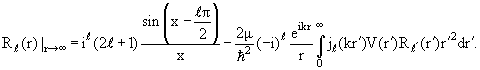 | (3.14) |
Здесь мы ограничились случаем потенциала конечного радиуса. Введем обозначение
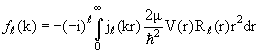 | (3.15) |
и запишем с его помощью асимптотическое выражение (3.14) более компактно:
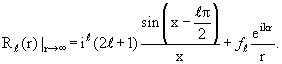 | (3.16) |
Подставляя это выражение в (3.2) и снова используя (3.4), получаем
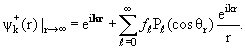 | (3.17) |
Отсюда видно, что ƒℓ − это коэффициент разложения амплитуды рассеяния по полиномам Лежандра:
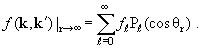 | (3.18) |
Мы будем называть их парциальными амплитудами рассеяния .
§ 3.2. Фазы рассеяния
Перестроим асимптотическое выражение (3.16), придав ему вид суперпозиции сходящейся и расходящейся сферических волн:
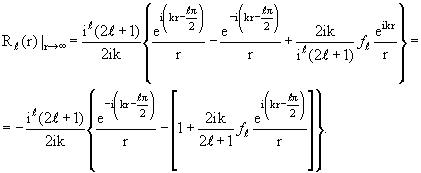 | (3.19) |
При движении частиц в поле, описываемом вещественным потенциалом, число частиц сохраняется. Это значит, что на асимптотически большом расстоянии от силового центра (r >> d) интенсивности сходящейся к центру сферической волны e -ikr /r и расходящейся из центра сферической волны e ikr /r равны друг другу. В свою очередь это означает, что на коэффициент перед расходящейся волной в (3.19) наложено условие:
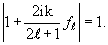 | (3.20) |
Условие (3.20) позволяет ввести для описания каждой парциальной амплитуды рассеяния ƒℓ(k), являющейся, вообще говоря, комплексной функцией энергии (импульса) частицы, одну вещественную функцию δℓ(k), называемую фазой рассеяния :
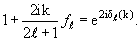 | (3.21) |
To же соотношение полезно записать и по-другому:
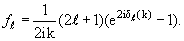 | (3.22) |
При каждом значении энергии (импульса) частицы фазы рассеяния δℓ полностью определяют асимптотический вид радиальной функции Rℓ(r) соответствующей парциальной волны. Подставляя (3.21) в (3.19), получаем
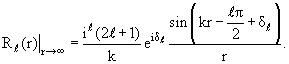 | (3.23) |
Как видно из (3.15), при «выключении» взаимодействия частицы с силовым центром (V→0) обращаются в нуль все парциальные амплитуды рассеяния ƒℓ, а вместе с ними, согласно (3.21), и все фазы δℓ. При этом асимптотическое выражение (3.23) превращается в асимптотику ℓ-й составляющей волновой функции свободной частицы:
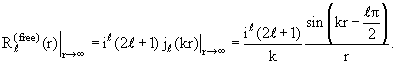 | (3.24) |
Сравнение выражений (3.24) и (3.23), отличающихся фазовым сдвигом в аргументе синуса, позволяет лучше понять смысл термина «фаза рассеяния».
Выразив через фазы рассеяния δℓ парциальные амплитуды ƒℓ, мы можем, пользуясь соотношениями (3.18) и (1.41), выразить через них полную амплитуду рассеяния, дифференциальное сечение, а затем и полное сечение рассеяния:
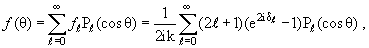 | (3.25) |
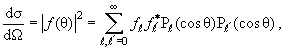 | (3.26) |
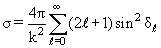 | (3.27) |
(при получении последней формулы мы воспользовались свойством ортонормированности полиномов Лежандра (3.5)). Формула (3.26) показывает, что угловое распределение рассеянных частиц зависит от интерференции между парциальными волнами с разными значениями орбитального момента частицы. Однако в полном сечении рассеяния а после интегрирования по всем углам вьшета рассеянной частицы эффект интерференции пропадает.
Сравнение формул (3.25) и (3.27) позволяет установить интересное соотношение между мнимой частью амплитуды рассеяния вперёд и полным сечением рассеяния:
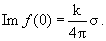 | (3.28) |
Это так называемая оптическая теорема . Доказанная нами для случая потенциального рассеяния, она (мы увидим это в дальнейшем) справедлива и в общем случае многоканального рассеяния. Мы будем обращаться к оптической теореме как к строгому и модельно независимому соотношению при оценке качества приближенных методов теории столкновений.
§ 3.3. Энергетическая зависимость фаз рассеяния при низких энергиях
При низких энергиях, когда импульс падающих частиц много меньше обратного радиуса взаимодействия (kd ℓ . Следовательно, из (3.29) вытекает
E ℓ+1/2 .
Это и есть искомая зависимость фаз рассеяния от энергии (импульса) частиц при малых энергиях. Она носит универсальный характер и присуща рассеянию на любом потенциале конечного радиуса.
§ 3.4. Методы вычисления фаз рассеяния
Точное решение задачи рассеяния с целью вычисления фаз рассеяния возможно лишь для отдельных искусственно придуманных потенциалов. На практике, когда приходится иметь дело с реалистическими потенциалами, фазы рассеяния всегда вычисляются приближенно, что связано либо с использованием тех или иных физических аппроксимаций, либо с проведением численного счета. Мы познакомимся с методами и того и другого родов.
а) Метод решения радиального уравнения Шредингера
Перепишем уравнение (3.3) в виде
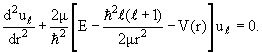 | (3.34) |
Здесь, как и при решении задачи о связанных состояниях частицы [1, с.114], функции uℓ(r) связаны с Rℓ(r) соотношением
| uℓ(r) = rRℓ(r) | (3.35) |
и при малых r ведут себя согласно степенному закону:
r ℓ+1
Поведение uℓ(r) при асимптотически больших г получаем из (3.23):
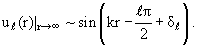 | (3.37) |
В общем случае уравнение (3.34) интегрируется численно, начиная от r = 0; для «разгонки» численного интегрирования удобно использовать свойство (3.36). Мы не будем вдаваться в чисто вычислительные аспекты этой процедуры. Для нас важно, что задачей интегрирования является построение всего «профиля» функции uℓ(r) с выходом при r → ∞ на асимптотику (3.37); при этом должно быть соблюдено условие непрерывности функции uℓ(r) и ее первой производной u‘ℓ(r) во всей области 0 > 1, r > d. Если энергия частицы Е и размеры области взаимодействия d таковы, что условие kr >> 1 не выполняется, то асимптотическое поведение (3.37) начинается далеко за границей области взаимодействия (r >> d). В этом случае не рационально доводить численное интегрирование до асимптотически больших значений r >> d, поскольку уже при r > d частица движется свободно и уравнение (3.3) переходит в уравнение движения свободной частицы:
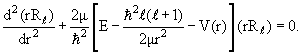 | (3.38) |
При Е > 0 его линейно независимыми решениями являются сферическая функция Бесселя jℓ(kr) и сферическая функция Неймана nℓ(kr), а общее решение уравнения (3.34) при r > d имеет вид
| Rℓ(r) = uℓ(r)/r = Aℓjℓ(kr) + Bℓnℓ(kr); r>d . | (3.39) |
Вместо констант интегрирования Аℓ и Вℓ удобно выбрать две другие:
| Aℓ = Cℓ cos δℓ; Вℓ = −Cℓ sin δℓ. | (3.40) |
| Rℓ(r) = uℓ(r)/r = Cℓ δℓ jℓ(kr) − sin δℓ nℓ(kr)>; r > d . | (3.41) |
С учетом (3.12) и (3.13) отсюда видно, что общее решение (3.39) имеет требуемую асимптотику (3.37).
Таким образом, практическая задача интегрирования уравнения (3.34) заключается в том, чтобы, начиная с r = 0, выйти в область свободного движения частицы r > d и «сшить» волновую функцию, найденную для внутренней области, с функцией (3.41). Пусть 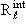
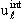
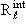
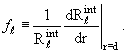 | (3.43) |
Исключая из (3.42) константу Cℓ (а вместе с ней и произвольно выбираемый при интегрировании уравнения (3.3) нормировочный множитель в 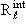
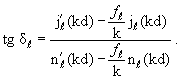 | (3.44) |
В качестве примера рассчитаем фазы рассеяния частицы на прямоугольной яме:
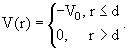 | (3.45) |
В этом случае для получения волновой функции Rℓ(r) во внутренней области не требуется численного интегрирования:
 (r) = const · jℓ(Kr) , (r) = const · jℓ(Kr) , | (3.46) |
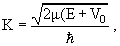 | (3.47) |
Отсюда находим логарифмическую производную (3.43):
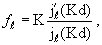 | (3.48) |
а далее по формуле (3.44) и фазу рассеяния:
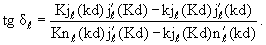 | (3.49) |
В качестве другого примера рассмотрим рассеяние частицы абсолютно твердой сферой. На поверхности такой сферы (r = d) «внешняя» волновая функция обращается в нуль:
| Rℓ(d) = 0 . | (3.50) |
Подставляя сюда (3.41), находим
| tg δℓ = jℓ(kd)/nℓ((kd) . | (3.51) |
В частности, при малых энергиях частицы отсюда получаем
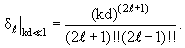 | (3.52) |
б) Теория возмущений
Если V(r) мало, то радиальную функцию Rℓ(r), входящую в формулу (3.29) для фазы и удовлетворяющую уравнению (3.10), можно заменить во внутренней области (r ℓ (2ℓ + 1)jℓ(kr). Тогда получаем приближенное выражение для фазы:
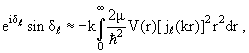 | (3.53) |
а вместе с ним и для парциальной амплитуды рассеяния:
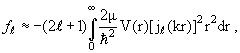 | (3.54) |
Согласно (3.54), амплитуда рассеяния ƒ(0) вещественна. С точки зрения оптической теоремы (3.28) такой результат, на первый взгляд, бессмыслен: мнимая часть амплитуды рассеяния вперед Im ƒ(0) равна нулю, а полное сечение σ, конечно, нет. Правда, если фазы рассеяния малы, то и мнимые части парциальных амплитуд Im ƒℓ = (2ℓ + l)k -1 sin 2 δℓ, интегральные парциальные сечения
σℓ = (4π/k 2 )(2ℓ + l) sin 2 δℓ квадратичны относительно δℓ; поэтому можно сказать, что при малых δℓ, оптическая теорема выполняется приближённо − с точностью до членов, пропорциональных δℓ 2 .
Таким образом, условие применимости теории возмущений для фаз − это малость фаз:
| |δℓ| борновским приближением для фаз рассеяния . Согласно (3.53) и (3.55), в этом приближении фазы вычисляются по формуле |
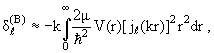 | (3.56) |
Она показывает, в частности, что если V(r) везде отрицательно (потенциал притяжения), то все борновские фазы 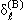
Выясним условия, при которых соблюдается требование малости фаз (3.55). Как и в §2.2, рассмотрим два предельных случая: длина волны частицы 
Если 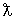
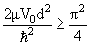 | (3.58) |
Если же в потенциальной яме имеются два-три уровня, то параметр (2μ| V |d 2 )/ћ 2 , которому пропорциональна величина |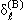
в) Метод фазовых функций
С точки зрения математики метод фазовых функций представляет собой особый способ решения радиального уравнения Шредингера (3.3), являющегося линейным дифференциальным уравнением второго порядка, или соответствующего ему интегрального уравнения (3.10). Он очень удобен для получения фаз рассеяния, так как по этому методу не требуется сначала вычислять в широкой области радиальные волновые функции задачи рассеяния и уже лишь потом, по их асимптотике, находить фазы. Сводя дело к решению нелинейного дифференциального уравнения первого порядка, метод фазовых функций очень удобен также с точки зрения выполнения численных расчетов на ЭВМ. Ниже мы изложим лишь основную идею этого метода.
Будем отправляться от интегрального уравнения (3.10), куда подставим функции Грина 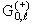
| Rℓ(r) = cℓ(r)jℓ(kr) + sℓ(r)nℓ(kr) , | (3.61) |
где cℓ(r) и sℓ(r) — две новые вспомогательные функции, определённые соотношениями
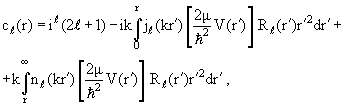 | (3.62) |
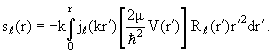 | (3.63) |
Используя (3.29), легко показать, что отношение этих функций при асимптотически больших г дает фазу рассеяния:
| tg δℓ = sℓ(∞)/cℓ(∞). | (3.64) |
Фазовой функцией называется функция δℓ(r), определенная соотношением
| tg δℓ(r) = sℓ(r)/cℓ(r) | (3.65) |
Как видно из (3.64), ее предел при r → ∞ есть фаза рассеяния:
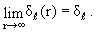 | (3.66) |
Легко убедиться путем непосредственной подстановки выражения (3.65), что фазовая функция δℓ(r) удовлетворяет при всех r уравнению
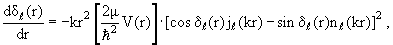 | (3.67) |
которое надо решать с дополнительным условием:
| δℓ(r=0) =0 | (3.68) |
Конечно, для получения предельного значения δℓ(∞) достаточно интегрировать уравнение (3.67) от нуля до границы области взаимодействия. Это хорошо видно также, если уравнению (3.67) придать вид интегрального уравнения:
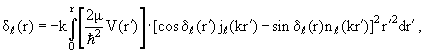 | (3.69) |
Уравнения (3.68) и (3.69) раскрывают физический смысл функции δℓ(r): фазовая функция δℓ(r), соответствующая заданному потенциалу V(r), − это фаза рассеяния частицы потенциалом, который «обрезан» в точке r, а на меньших расстояниях совпадает с V(r).
Упражнения
3.1. Найти связь между функцией Грина 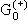
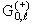
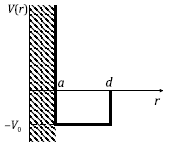 |
3.2. Получить общую формулу для фаз рассеяния δℓ частицы потенциальной ямой глубины V0 радиуса d с бесконечной отталкивающей серединой paдиуса а в центре ямы (см. рис.).
3.3. Вычислить борновскую фазу s-волны 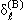
http://nuclphys.sinp.msu.ru/qti/qti_03.htm