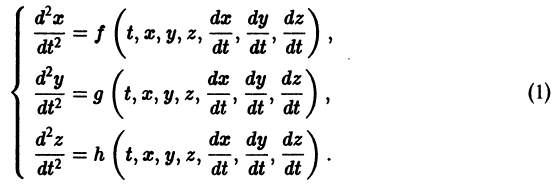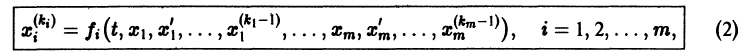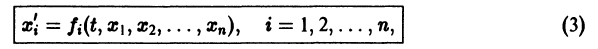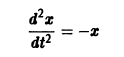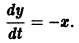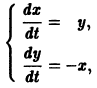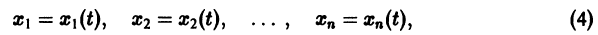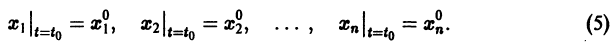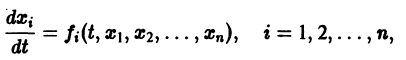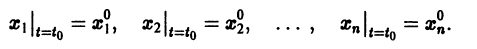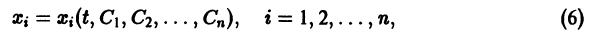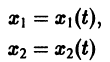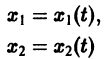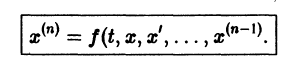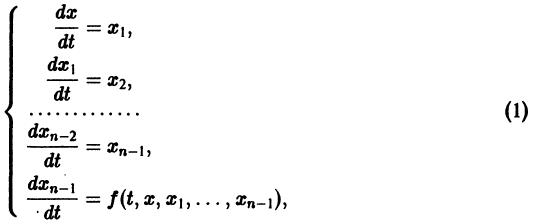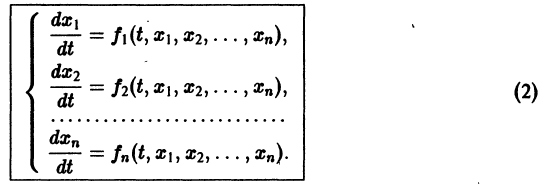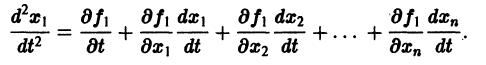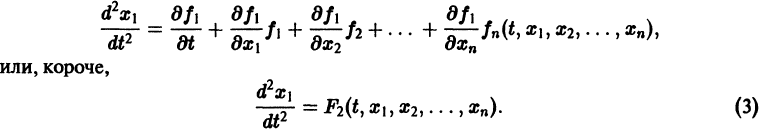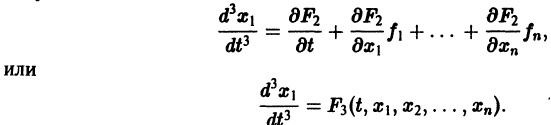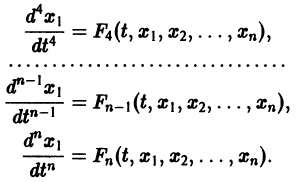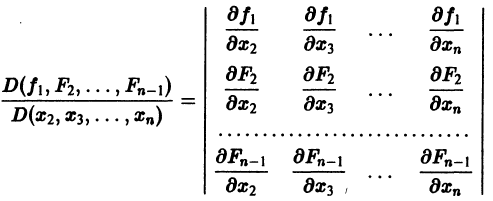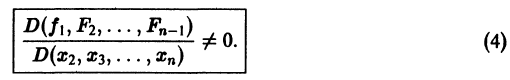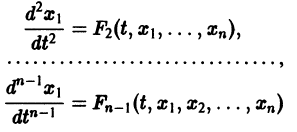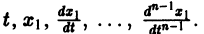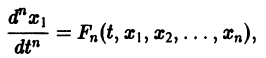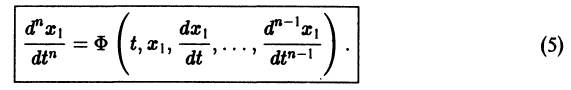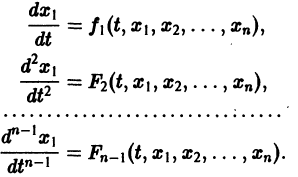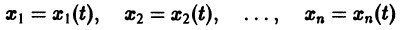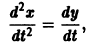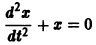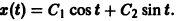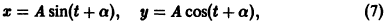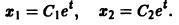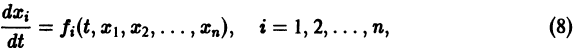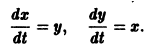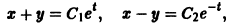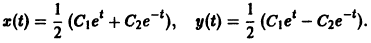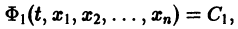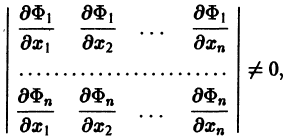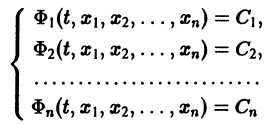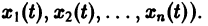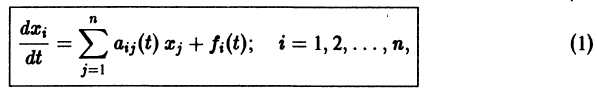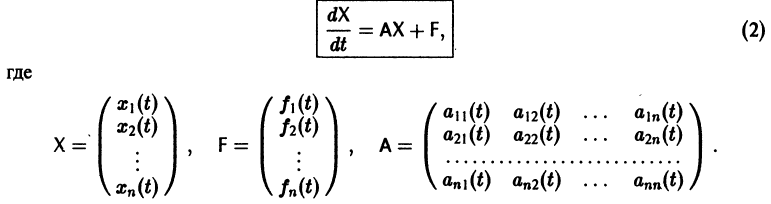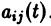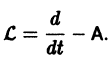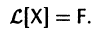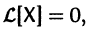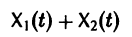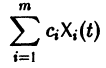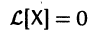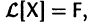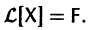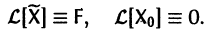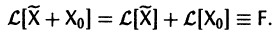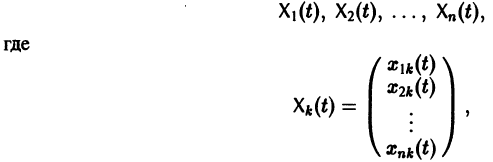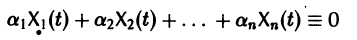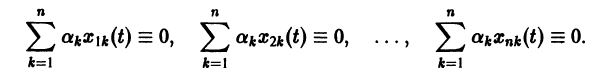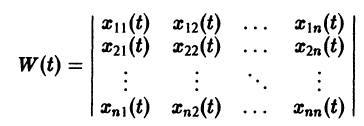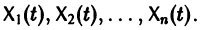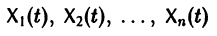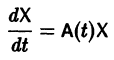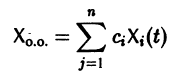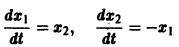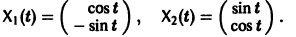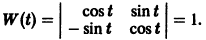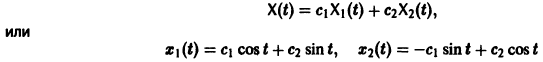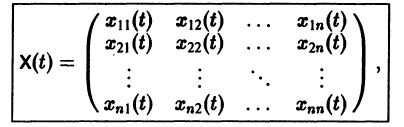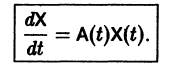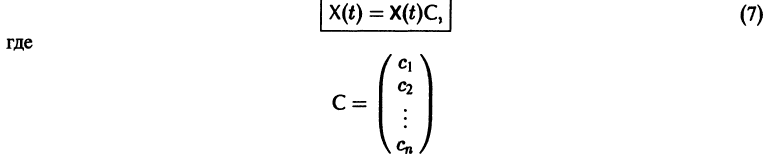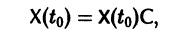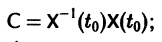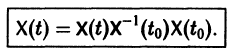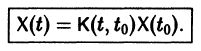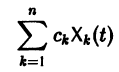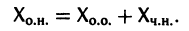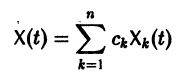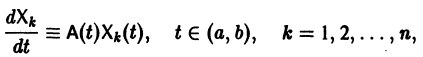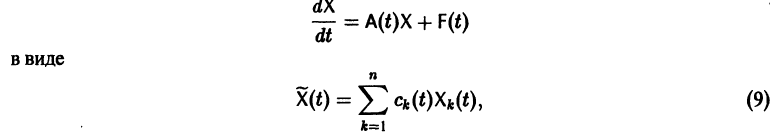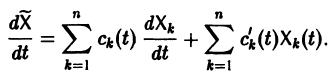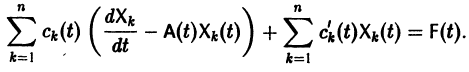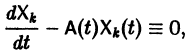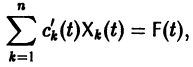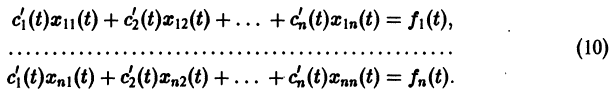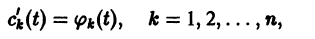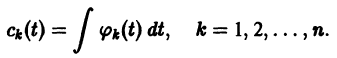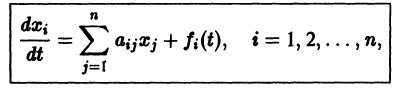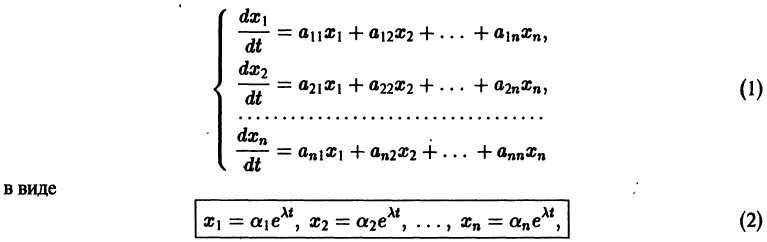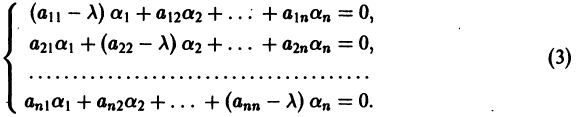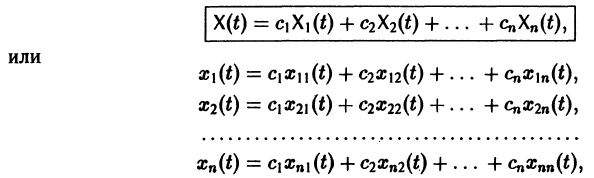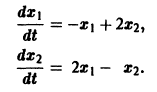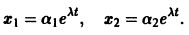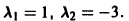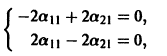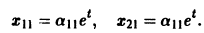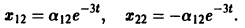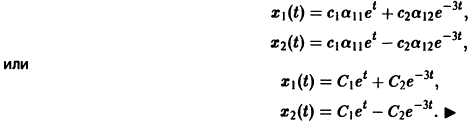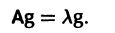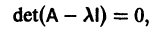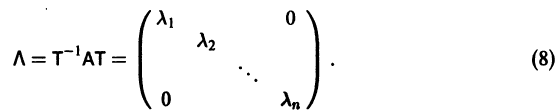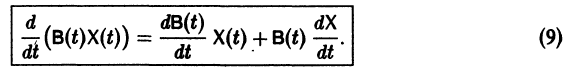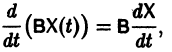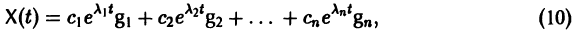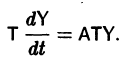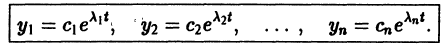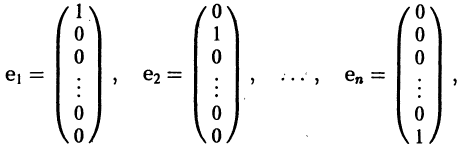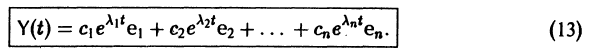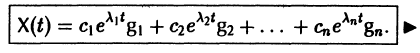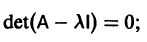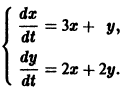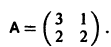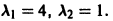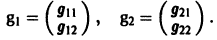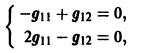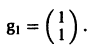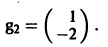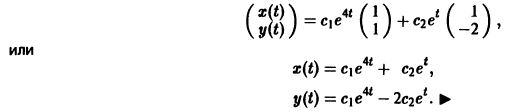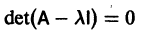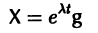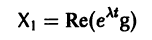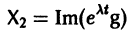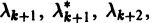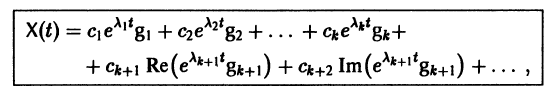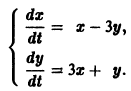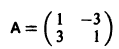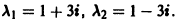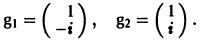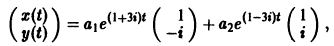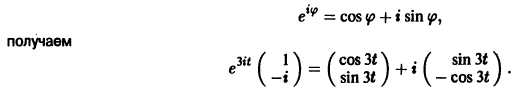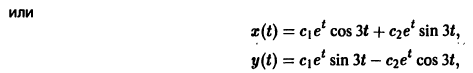Методы интегрирования обыкновенных дифференциальных уравнений — Матвеев Н.М.
Название: Методы интегрирования обыкновенных дифференциальных уравнений. 1967.
Автор: Матвеев Н.М.
В книге даются основные понятия и определения теории обыкновенных дифференциальных уравнений, излагаются наиболее важные методы интегрирования, доказываются теоремы существования решений и исследуются свойства последних. Являясь учебником для студентов университетов, она может быть использована в педагогических институтах и в технических ВУЗах, а также студентами-заочниками и лицами, самостоятельно изучающими теорию обыкновенных дифференциальных уравнений.
Несмотря на большое количество результатов, полученные в общей теории дифференциальных уравнений, в том числе, особенно, в последние годы, элементарные методы интегрирования по-прежнему остаются важными методами интегрирования.
В настоящей книге излагаются основные методы интегрирования различных типов обыкновенных дифференциальных уравнений, доказаны основные теоремы существования решений (методы доказательства которых позволяют строить приближенные решения) и теоремы о зависимости решений от самого уравнения и от начальных данных, а также дается понятие об основных задачах общей теории обыкновенных дифференциальных уравнений.
При изложении различных методов интегрирования мы пытаемся везде, где это возможно, получить решение в виде элементарных функций или квадратур элементарных функций. Б тех случаях, когда это невозможно, указываются методы интегрирования в смысле более широкой постановки задачи При этом используются некоторые результаты общей теории обыкновенных дифференциальных уравнений.
ОГЛАВЛЕНИЕ
Предисловие 3
Введение 6
Глава первая
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. Уравнения, интегрируемые в квадратурах 13
1. Основные понятия и определения 13
1. Понятие об уравнении первого порядка, разрешенном, относительно производной (13).
2. Решение уравнения (14)
3. Неявное и параметрическое задания решения (15)
4. Геометрическое истолкование (16).
5. Задача Коши (21).
6. Достаточное условие существования решения задачи Коши (24).
7. Достаточные условия существования н единственности решения задачи Коши (25).
8. Общее решение (28).
9. Общий интеграл. Общее решение в параметрической форме (31).
10. Частное решение (32).
11. Особое решение (33).
12. Нахождение кривых, подозрительных на особое решение по дифференциальному уравнению (35).
13. Отсутствие особых решений у уравнения первого порядка с правой частью, рациональной относительно у (36).
14. Огибающая семейства интегральных кривых как особое решение (37).
15. Нахождение кривых, подозрительных на особое решение в процессе построения общего решения (общего интеграла) (41).
16. Понятие об интеграле дифференциального уравнения (41).
17. Теорема о зависимости любых двух интегралов одного и того же уравнения (46).
18. Замечание об интегрируемости в квадратурах (48).
2. Неполные уравнения 50
19. Уравнение, не содержащее искомой функции (50).
20. Уравнение, не содержащее независимой переменной (52)
3. Уравнение с разделяющимися переменными 55
21. Построение общего интеграла (55).
22. Особые решения (58).
23. Примеры (58)
4. Однородное уравнение 60
24. Построение общего интеграла (61).
25. Особые решения (62).
26. Примеры (62).
27. Геометрическое свойство интегральных кривых однородного уравнения (63).
28. Простейшее уравнение, приводящееся к однородному (65)
5. Обобщенное однородное уравнение 66
29. Построение общего интеграла. Особые решения (66).
30. Пример (68)
6. Линейное уравнение 68
31. Понятие о линейном уравнении (68).
32. Существование и единственность решения задачи Коши. Общие свойства линейного уравнения (60).
33. Построение общего решения однородного линейного уравнения (71).
34. Свойства решений однородного линейного уравнения (74).
35. Структура общего решения неоднородного линейного уравнения (75).
36. Метод вариации произвольной постоянной (метод Лагранжа) (76).
37. Примеры (80).
38. Геометрическое свойство интегральных кривых линейного уравнения (81)
7. Уравнение Бернулли 83
39. Построение общего решения (83).
40. Особое решение (83).
41. Пример (41)
8. Уравнение Дарбу 85
42. Построение общего интеграла. Особые решения (85).
43. Пример (85).
9. Уравнение Риккати 86
44. Существование и единственность решения задачи Коши (86)
45. Общие свойства уравнения Риккати (88).
46. Приведение уравнения Риккати к каноническому виду (89).
47. Простейшие случаи интегрируемости в квадратурах (90).
48. Построение общего решения в случае, когда «известно одно частное решение (91).
49. Структура общего решения (93).
50. Построение общего решения в случае, когда известны два или три частных решения (94).
51. Специальное уравнение Риккати (94)
11. Уравнение, в полных дифференциалах 96
52. Понятие об уравнении в полных дифференциалах (96).
53. Признак уравнения в полных дифференциалах. Построение общего интеграла (98).
54. Решение задачи Коши (100)
12. Интегрирующий множитель. Простейшие случаи нахождения интегрирующего множителя 101
55. Понятие об интегрирующем множителе (101).
56. Случай интегрирующего множителя, зависящего только от х (103).
57. Случай интегрирующею множителя, зависящего только от y (104).
58. Случай интегрирующего множителя зависящего от (х, у) (104).
59. Интегрирующий множитель и особые решения (103).
60. Интегрирующий множитель уравнения с разделяющимися непеменными (106).
61. Интегрирующий множитель однородного уравнения (106)
13. Интегрирующий множитель. Общая теория 108
62. Теорема о существовании интегрирующего множителя (108).
63. Теорема о неединственности интегрирующего множителя (109).
64. Теорема об общем виде интегрирующего множителя и се следствие (110).
65. Один общий способ нахождения интегрирующего множителя (112).
Глава вторая. Уравнения первого порядка, не разрешенные относительно производной. Уравнения, интегрируемые в квадратурах ИЗ
1. Основные понятия и определения ИЗ
77. Общий случай уравнения первого порядка, не разрешенного относительно производной (ИЗ).
67. Примеры (118).
68. Нахождение кривых подозрительных па особое решение по дифференциальному уравнению (122).
69. Огибающая семейства интегральных кривых как особое решение (124)
2. Неполные уравнения 125
70. Уравнение, содержащее только производную (125).
71. Уравнение, не содержащее искомой функции (127).
72. Уравнение, не содержащее независимой переменной (131).
73. Обобщенное однородное уравнение (132)
3. Общий метод введения параметра 133
74. Приведение уравнения, . не разрешенного относительно производной, к уравнению, разрешенному относительно производной. Общий случай (133).
75. Случай, когда уравнение разрешимо относительно искомой функции (134).
76. Случай, когда уравнение разрешимо относительно независимой переменной (135).
77. Уравнение Лагранжа (136)
78. Уравнение Клеро (138)
4. Задача о траекториях 141
79. Зачача о траекториях на плоскости в случае декартовых координат (141).
80. Примеры (143).
81. Случай полярных координат
Глава третья. Уравнения высших порядков. Общие вопросы. Простейшие уравнения n-го порядка 48
1. Основные понятия и определения 148
82. Предварительные замечания (148).
83. Геометрическое истолкование (149).
84. Механическое истолкование уравнения второго порядка (149).
85. Задача Коши (150).
86. Достаточные услогшя существования и единственности решения задачи Коши (153).
87. Понятие о граничной (краевой) задаче (154).
88. Общее решение (156).
89. Общий интеграл (157).
90. Общее решение в параметрической форме (158).
91. Частное решение (158).
92. Особое решение (158).
93. Промежуточные интегралы. Первые интегралы (159).
94. Замечание об уравнения n-го порядка, не разрешенном относительно старшей производной (160).
2. Уравнения, интегрируемые в квадратах, и уравнения, допускающие понижение порядка 161
95. Уравнение, содержащее только независимую переменную и производную порядка п (161).
96. Уравнение, не содержащее искомой функции, и уравнение, не содержащее искомой функции и последовательных первых производных (168).
97. Уравнение, не содержащее независимой переменной (171).
98. Уравнение, однородное относительно искомой функции н ее производных (173).
99. Обобщенное однородное уравнение (174).
100. Уравнение, левая часть которого есть точная производная (177)
Глава четвертая. Системы обыкновенных дифференциальных уравнений. Общие вопросы. 180
1. Нормальные системы дифференциальных уравнений 180
101. Понятие о нормальной системе. Линейная система (180).
102. Решение системы (181).
103. Геометрическое истолкование нормальной системы (182).
104. Механическое истолкование нормальной системы (183).
105. Задача Коши (180).
106. Достаточные условия существования и единственности решения задачи Коши (188).
107. Общее решение (189).
108. Частное решение (191).
109. Особое решение (191).
110. Понятие об интеграле нормальной системы. Первые интегралы. Общий интеграл. Число независимых интегралов (192).
111. Понижение порядка системы при помощи первых интегралов (203).
112. Приведение уравнения n-го порядка к системе уравнений первого порядка и обратная задача (205).
113. Одни общий способ интегрирования нормальной системы двух уравнений, правые части которых удовлетворяют условиям Коши — Римана (210).
114. Понятие с системе уравнений высших порядков (211).
115. Построение всего множества нормальных систем дифференциальных, уравнений, имеющих заданную траекторию (213)
2. Системы дифференциальных уравнений в симметрической форме 216
116. Понятие о системе обыкновенных дифференциальных уравнений в симметрической форме. Приведение нормальной системы к системе в симметрической форме (216).
117. Интегралы, первые интегралы и общий интеграл системы дифференциальных уравнений в симметрической форме (218).
Глава пятая. Теоремы существования 225
1. Теорема существования и единственности решения задачи Коши (теорема Пикара) 225
118. Предварительные замечания (225).
119. Формулировка теоремы Пикара для нормальной системы уравнений (227).
120. Доказательство теоремы Пикара для нормальной системы двух уравнений (229).
121. Замечание о выборе нулевого приближения (241).
122. Случай одностороннего интервала изменения независимой переменной (241).
123. Случай области, не ограниченной по искомым функциям (242).
124. Случай области, не ограниченной по всем переменным (243).
125. О продолжении решения, определяемого теоремой Пикара (247).
126. Теорема Пикара для линейной системы дифференциальных уравнений (250).
127. О решении однородной линейной системы с нулевыми начальными значениями искомых функций (254). 128. Теорема Пикара для уравнения п-го порядка (255).
129. Теорема Пикара для линейного уравнения n-го порядка (257).
130. О решении однородного линейного уравнения n-го порядка с нулевыми начальными значениями искомой функции и ее производных (258).
2. Теоремы о непрерывности и дифференцируемости решения как функции от параметров и начальных данных. Понятие об устойчивости решения в смысле Ляпунова 259
131. Теорема о непрерывной зависимости решения нормальной системы от параметров (259).
132. Теорема о непрерывной зависимости решения нормальнон системы от начальных данных (267).
133. Понятие об устойчивости решения (движения) в смысле Ляпунова (272).
134. Теорема о дифференцируемости решения по начальным данным (279).
135. Обобщения (291)
3. Теорема существования общего решения 292
136. Теорема существования общего решения нормальной системы дифференциальных уравнений (292).
137. Замечания (297).
138. Доказательство существования п независимых интегралов нормальной системы п уравнений (297).
4. Особые течки 299
139. Особые точки уравнения первого порядка, разрешенного относительно производной (299).
140. Особые точки нормальной системы дифференциальных уравнений. Точки равновесия (покоя) (301).
141. Поведение интегральных . кривых уравнения с дробно-линейной однородной правой частью а окрестности особой точки (305).
142. Один физический пример (320).
143. Понятие о проблеме центра и фокуса (322)
§ 5. Теорема существования и единственности голоморфного решения задачи Коши (теорема Коши) 327
144. Понятие о голоморфном решении (327). 145. Понятие о мажоранте (328). 146. Формулировка теоремы Коши для нормальной системы п уравнений (330). 147. Доказательство теоремы Коши для нормальной системы двух уравнений (332). 148. Теорема Коши для линейной системы (341). 149. Примеры существования голоморфных решений в случае невыполнения условия теоремы Коши (346). 150. Теорема Коши для уравнения иго порядка, разрешенного относительно старшей производной (348). 151. Теорема Коши для линейного уравнения n-го порядка (350). 152. Теорема о голоморфности решения относительно параметра (351).
6. Теорема существования решения задачи Коши (теорема Пеано) 352
153. Теорема Арцеля (352).
154. Теорема существования решения дифференциального уравнения с непрерывной правой частью (теорема Псано) (355).
155. Теорема Пеано для нормальной системы (362).
Глава шестая. Общая теория линейных дифференциальных уравнений n-го порядка 363
1. Общие свойства линейного уравнения 363
136. Предварительные замечания (363).
157. Инвариантность линейного уравнении относительно любого преобразования независимой переменной (365).
158. Инвариантность линейного уравнения относительно линейного преобразовании искомой функции (366).
2. Однородное линейное уравнение n-го порядка 367
159. Свойства решений (367).
160. Понятие о линейной независимости функции (371).
161. Необходимое условие линейной зависимости п функций (374).
162. Необходимое и достаточное условие линейной независимости п решений однородного линейного уравнения n-го порядка (375).
163. Формула Остроградского — Лиувилля (377).
164. Понятие о фундаментальной системе решений (379).
165. Доказательство существования фундаментальной системы решений (379).
106. Построение общего решения (380).
167. Число линейно-независимых решений однородного линейного уравнения n-го порядка (384).
168. Построение однородного линейного уравнения, имеющего заданную фундаментальную систему решений (384). 169. Понижение порядка однородного линейного уравнения при помощи линейно независимых частных решений (387).
3. Неоднородное линейное уравнение п-го порядка 389
170. Структура общего решения неоднородного уравнения (389).
171. Метод вариации произвольных постоянных (метод Лагранжа) (391).
172. Метод Коши (394).
Глава седьмая. Линейные уравнения n-го порядка с постоянными коэффициентами 398
1. Однородное уравнение 398
173 Предварительные замечания (398).
174. Построение фундаментальной системы решении и общего решения однородного уравнения в случае различных корней характеристического уравнения (398).
175. Случай наличия кратных корней характеристического уравнения (403).
176. Однородное линейное уравнение второго порядка с постоянными коэффициентами (406).
2. Неоднородное уравнение 408
177. Предварительные замечания (408).
178. Нахождение частного решения неоднородного уравнения методом неопределенных коэффициентов (408). 179. Неоднородное линейное уравнение второго порядка с постоянными коэффициентами (112).
3. Линейные уравнения второго порядка с постоянными коэффициентами и колебательные явления 417
180. Свободные колебания (417).
181. Вынужденные колебания (421).
4. Некоторые линейные уравнения n-го порядка, приводящиеся к уравнениям с постоянными коэффициентами 423
182. Приведение однородного линейного уравнения п-го порядка к уравнению с постоянными коэффициентами при помощи замены независимой переменной (42.3).
183. Линейное уравнение Эйлера (424).
184. Уравнение Чебышева (420).
185. Приведение однородного линейного уравнения 1-го порядка к уравнению с постоянными коэффициентами при помощи линейной замены искомой функции (430).
Глава восьмая. Некоторые вопросы теории однородных линейных уравнений второго порядка 431
1. Приведение к простейшим форма 431
186. Приведение к уравнению, не содержащему члена с первой производной (431). 187. Приведение к самосопряженному виду (433).
§ 2. Понижение порядка 435
188. Построение общего решения однородного линейного уравнения второго порядка в случае, когда известно одно частное решение (435).
189. Связь меж лу однородным линейным уравнением второго порядка и уравнением Риккати (437).
3. Интегрирование при помощи степенных рядов 438
100. Представление решений однородного линейного уравнения второю порядка в виде степенных рядов (438). 101. Представление решений в окрестности особой точки в виде обобщенных степенных рядом (439).
192. Уравнение Бесселя (449).
193. Гипергеометрическое дифференциальное уравнение ( 459).
4. Колебательный характер решений однородных линейных уравнений второго порядка 464
194. Колеблющиеся и неколеблющиеся решения (464).
193. Теорема Штурма (467).
196. Теорема сравнения (468).
Глава девятая. Общая теория линейных систем дифференциальных уравнений 472
1. Однородные линейные системы 472
197. Предварительные замечания (472).
198. Свойства решений однородной системы (474).
199. Понятие о линейной независимости систем функций (477).
200. Необходимое условие линейной зависимости п систем функций (479).
201. Необходимое и достаточное условие линейной независимости п решений однородной линейной системы п уравнений (480).
202. Формула Остроградского- Лиупилля -Якоби (480).
203. Понятие о фундаментальной системе решений (482).
204. Теорема о существовании фундаментальной системы решений (482).
205. Построение общего решения (483).
206. Число линейнонезависимых решений однородной линейной системы п уравнений. Первые интегралы (485). 207. Понятие о сопряженной (присоединенной) системе (480).
208. Построение однородной линейной системы уравнений, имеющей заданную фундаментальную систему решений (489).
2 Неоднородные линейные системы 490
209. Структура общего решения неоднородной системы (490).
210. Метод вариации произвольных постоянных (метод Лагранжа) (491).
Глава десятая. Линейные системы дифференциальных уравнений с постоянными коэффициентами 494
1. Метод Эйлера 494
211. Предварительные замечания (494).
212. Построение фундаментальной системы решений н общего решения однородной линейной системы в случае различных корней характеристического уравнения (495).
213. Случай наличия кратных корней характеристического уравнения (500).
214. Теорема об асимптотической устойчивости (в смысле Ляпунова) нулевого решения однородной линейной системы с постоянными коэффициентами (502).
215. Теорема о неустойчивости нулевого решения однородной линейной системы с постоянными коэффициентами (503).
216. Приведение однородной линейной системы к системе с постоянными .коэффициентами при помощи замены независимой переменной (503).
217. Интегрирование неоднородной линейной системы с постоянными коэффициентами методом вариации произвольных постоянных (505).
2. Другие методы интегрирования линейных систем с ‘постоянными коэффициентами 505
218. Интегрирование линейной системы с постоянными коэффициентами при помощи приведения ее к уравнению п-го порядка (метод исключении) (505).
219.Метод Даламбсра (507).
§ 3. Линейные системы с постоянными коэффициентами, содержащие производные выше первого порядка . 509
220. Метод исключения (509).
221. Метод Даламбера (509).
Глава одиннадцатая. Матричный метод решения однородных линейных систем 511
1. Запись и решение однородной линейной системы в матричной форме 511
222. Предварительные замечания (511).
223. Построение матричного уравнения, равносильного однородной линейной системе (516).
224. Два общих свойства матричного уравнения, соответствующего однородной линейной системе (519).
225. Основные свойства интегральной матрицы (520).
226. Случай Лаппо — Данилевского (522).
227. Сопряженное (присоединенное) матричное уравнение (523)
2 Интегрирование однородной линейной системы с постоянными коэффициентами 525
228. Структура фундаментальной системы решений однородной линейной системы дифференциальных уравнений с постоянными коэффициентами. Группы решений (525).
229. Приведение однородной линейной системы с постоянными коэффициентами к каноническому виду (530). 230. Понятие о приводимых 1 системах (537).
Глава двенадцатая. Понятие об уравнениях с частными производными первого порядка 539
1. Однородное линейное уравнение 539
231. Связь между однородным линейным уравнением с частными производными первого порядка и соответствующей ему системой обыкновенных дифференциальных уравнений и симметрической форме (539). 232. Построение общего решения однородного линейного уравнения (512).
233. Решение задачи Коши для однородного линейного уравнения (545).
2. Неоднородное линейное уравнение 548
234. Построение общего решения неоднородного линейного уравнения (518).
235. Решение задачи Коши для неоднородного линейного уравнения (551).
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Методы интегрирования обыкновенных дифференциальных уравнений — Матвеев Н.М. — fileskachat.com, быстрое и бесплатное скачивание.
Скачать djvu
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу
Системы дифференциальных уравнений с примерами решения и образцами выполнения
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.
Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 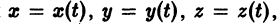
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 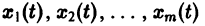
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
Если 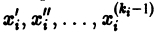
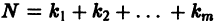
Например, одно уравнение
является мастным случаем канонической системы. Положив 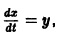
В результате получаем нормальную систему уравнений
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
дифференцируемых на интервале а
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
и пусть функции 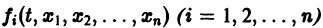
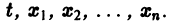

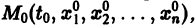

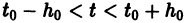
Определение:
Система n функций
зависящих от t и n произвольных постоянных 

1) при любых допустимых значениях 
2) в области 
Решения, получающиеся из общего при конкретных значениях постоянных 
Обратимся для наглядности к нормальной системе двух уравнений,
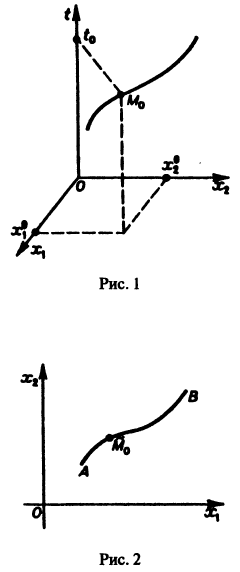
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 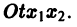
системы (7), принимающее при 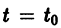
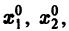
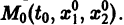
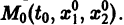
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
системы — как параметрические уравнения кривой на плоскости 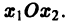
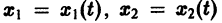
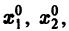
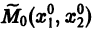
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
Введя новые функции 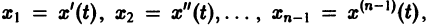
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
Продифференцируем первое из уравнений (2) по t. Имеем
Заменяя в правой части производные 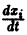
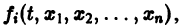
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
Продолжая этот процесс, найдем
Предположим, что определитель
(якобиан системы функций 
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
будет разрешима относительно неизвестных 

Внося найденные выражения в уравнение
получим одно уравнение n-го порядка
Из самого способа его построения следует, что если 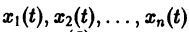
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 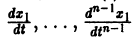
от t в систему уравнений
По предположению эту систему можно разрешить относительно 

Можно показать, что так построенная система функций
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему
Дифференцируя первое уравнение системы, имеем
откуда, используя второе уравнение, получаем
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
В силу первого уравнения системы находим функцию
Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
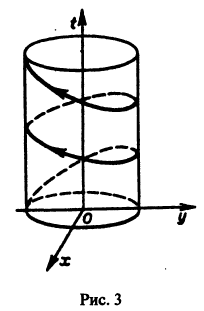
Функции x(t), y(t) можно представить в виде
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 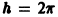
Исключая в формулах (7) параметр t, получаем уравнение
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
Может оказаться, что функции 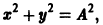
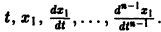
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
Мы нашли два конечных уравнения
из которых легко определяется общее решение системы:
Одна интегрируемая комбинация дает возможность получить одно уравнение
связывающее независимую переменную t и неизвестные функции 
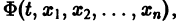
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций 
то задача интефирования системы (8) решена (так как из системы
определяются все неизвестные функции
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
или, в матричной форме,
Теорема:
Если все функции 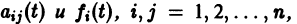
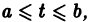
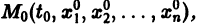
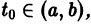
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, 
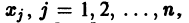
Введем линейный оператор
Тогда система (2) запишется в виде
Если матрица F — нулевая, т. е. 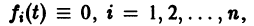
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
двух решений 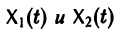
Следствие:
с произвольными постоянными коэффициентами сi решений 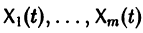
является решением той же системы.
Теорема:
Если 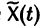
a Xo(t) — решение соответствующей однородной системы
будет решением неоднородной системы
Действительно, по условию,
Пользуясь свойством аддитивности оператора 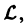
Это означает, что сумма 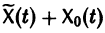
Определение:
называются линейно зависимыми на интервале a
при 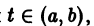

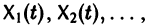
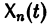
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
называется определителем Вронского системы векторов
Определение:
Пусть имеем линейную однородную систему
где 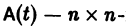
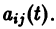
линейной однородной системы (6), линейно независимых на интервале а
с непрерывными на отрезке 
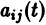
(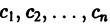
Пример:
имеет, как нетрудно проверить, решения
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Общее решение системы имеет вид
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
столбцами которой являются линейно независимые решения 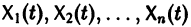
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
Матрица 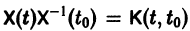
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 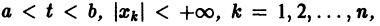
с непрерывными на отрезке 
соответствующей однородной системы и какого-нибудь частного решения 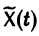
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
есть общее решение однородной системы (6), тогда
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
где 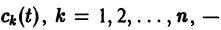
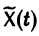
Подставляя 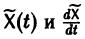
то для определения 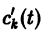
или, в развернутом виде,
Система (10) есть линейная алгебраическая система относительно 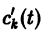
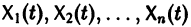
где 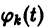
Подставляя эти значения 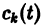
(здесь под символом 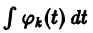
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
в которой все коэффициенты 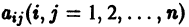
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
Будем искать решение системы
где 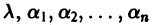
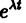
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно 


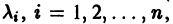
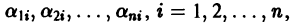
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
где 
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
Ищем решение в виде
имеет корни
Система (3) для определения a1, а2 выглядит так:
Подставляя в (*) 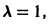
откуда а21 = а11. Следовательно,
Полагая в 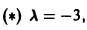
Общее решение данной системы:
Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

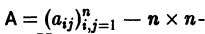
Напомним некоторые понятия из линейной алгебры. Вектор 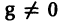
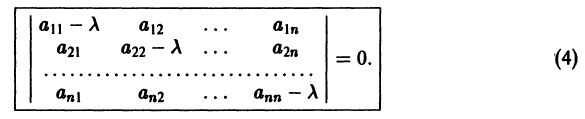
Число 
где I — единичная матрица.
Будем предполагать, что все собственные значения 
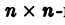
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
Введем еще следующие понятия. Пусть В(t) — 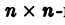








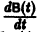
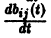
Пусть B(t) — n х n-матрица,
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
В частности, если В — постоянная матрица, то
так как 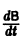
Теорема:
Если собственные значения 
где g1, g2,…, gn — собственные векторы-столбцы матрицы А, 
Введем новый неизвестный вектор-столбец Y(t) по формуле
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
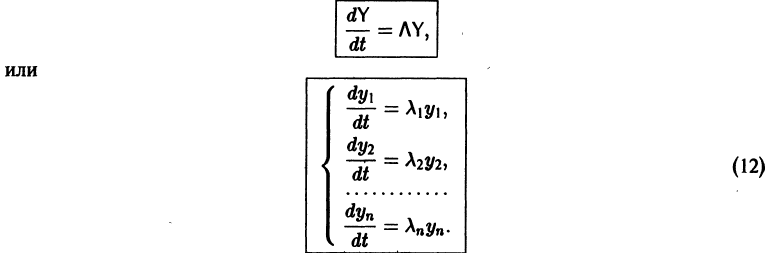
Умножая обе части последнего соотношения слева на 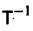
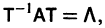
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
Здесь 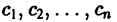
Вводя единичные n-мерные векторы-столбцы
решение Y(t) можно представить в виде
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 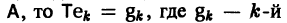
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения 
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
Матрица А системы имеет вид
1) Составляем характеристическое уравнение
Корни характеристического уравнения
2) Находим собственные векторы
Для 
откуда g11 = g12, так что
Аналогично для 
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 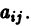
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем 




При комплексном 
системы (7) также будет комплексным. Действительная часть
этого решения являются решениями системы (7). Собственному значению 



Пусть 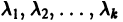
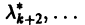
где сi — произвольные постоянные.
Пример:
1) Характеристическое уравнение системы
Его корни
2) Собственные векторы матриц
3) Решение системы
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
Следовательно, всякое действительное решение системы имеет
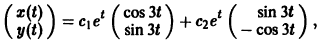
где с1, с2 — произвольные действительные числа.
Понятие о системах дифференциальных уравнений


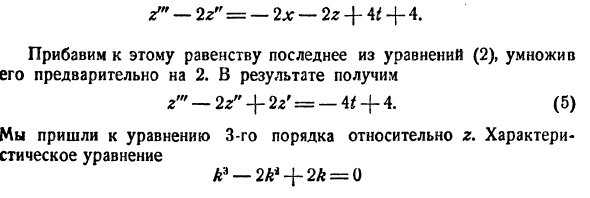

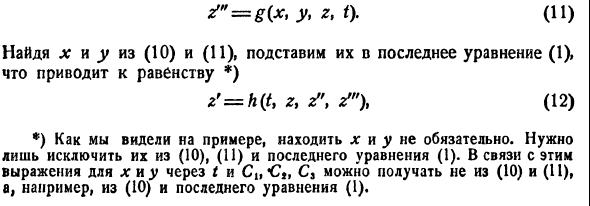

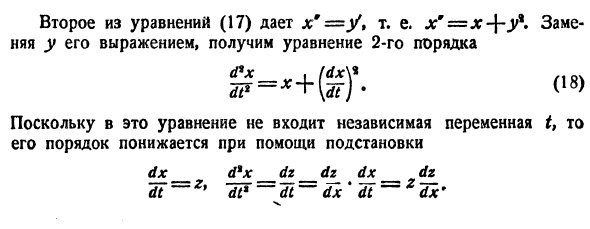

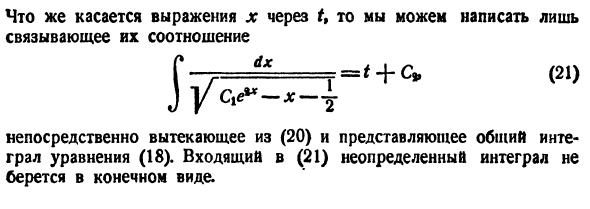

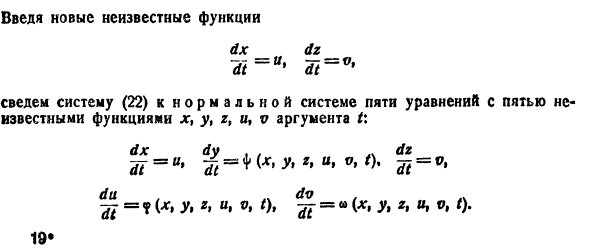
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Системы дифференциальных уравнений. Методы интегрирования. Метод исключения
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Основные понятия и определения К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции х = x(t), у = y(t), z = z(t), выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид Здесь x, у, z — координаты движущейся точки, t — время, f,g,h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями аргумента t, назовем канонической систему вида разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций, называется нормальной. Если принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из уравнений.
Поэтому достаточно рассматривать лишь нормальные системы. Например, одно уравнение является частным случаем канонической системы. Положив ^ = у, в силу исходного уравнения будем иметь В результате получаем нормальную систему уравнений СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕН Методы интегрирования Метод исключения Метод интегрируемых комбинаций Системы линейных дифференциальных уравнений Фундаментальная матрица Метод вариации постоянных Системы линейных дифференциальных уравнений с постоянными коэффициентами Матричный метод эквивалентную исходному уравнению. Определение 1.
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система п функций ‘ дифференцируемых на интервале , обращающая уравнения системы (3) в тождества по t на интервале (а, Ь). Задача Коши для системы (3) формулируется так: найти решение (4) системы, удовлетворяющее при t = to начальным условиям Теорема 1 (существования и единственности решения задами Коим). Пусть имеем нормальную систему дифференциальных уравнений и пусть функции определены в некоторой (n + 1)-мерной области D изменения переменных t, Х\, х 2, . хп.
Если существует окрестность ft тонки в которой функции ft непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным Х\, х2, . хп, то найдется интервал to — Л0 изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям Определение 2.
Система п функций зависящих от tun произвольных постоянных называется общим решением нормальной системы (3) в некоторой области П существования и единственности решения задачи Коши, если 1) при любых допустимых значениях система функций (6) обращает уравнения (3) в тождества, 2) в области П функции (6) решают любую задачу Коши. Решения, получающиеся из общего при конкретных значениях постоянных называются частными решениями.
Обратимся для наглядности к нормальной системе двух уравнений, Будем рассматривать систему значений t> Х\, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат Otx\х2. Решение системы (7), принимающее при t — to значения , определяет в пространстве некоторую линию, проходящую через точку )- Эта линия называется интегральной кривой нормальной системы (7). Задача Ко-ши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t> Х\, х2 найти интегральную кривую, проходящую через данную точку Mo(to,x1,x2) (рис. 1).
Теорема 1 устанавливает существование и единственность такой кривой. Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение системы — как параметрические уравнения кривой на плоскости х\Ох2. Эту плоскость переменных Х\Х2 называют фазовой плоскостью. В фазовой плоскости решение (0 системы (7), принимающее при t = t0 начальные значения х°<, х2, изображается кривой АВ, проходящей через точку ). Эту кривую называют траекторией системы (фазовой траекторией).
Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость.
По интегральной кривой фазовая траектория определяется однозначно, но не наоборот. § 2. Методы интегрирования систем дифференциальных уравнений 2.1. Метод исключения Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной, Введя новые функции уравнение следующей нормальной системой п уравнений: заменим это одно уравнение n-го порядка эквивалентно нормальной системе (1).
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка п. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений. Делается это так. Пусть имеем нормальную систему дифференциальных уравнений Продифференцируем первое из уравнений (2) по t. Имеем Заменяя в правой части произв или, короче, Уравнение (3) снова дифференцируем по t.
Принимая во внимание систему (2), получим или Продолжая этот процесс, найдем Предположим, что определитель (якобиан системы функций отличен от нуля при рассматриваемых значениях Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений будет разрешима относительно неизвестных выразятся через Внося найденные выражения в уравнение получим одно уравнение n-го порядка Из самого способа его построения следует, что если ) есть решения системы (2), то функция X\(t) будет решением уравнения (5).
Обратно, пусть — решение уравнения (5). Дифференцируя это решение по t, вычислим и подставим найденные значения как известные функции По предположению эту систему можно разрешить относительно , хп как функции от t. Можно показать, что так построенная система функций составляет решение системы дифференциальных уравнений (2). Пример. Требуется проинтегрировать систему Дифференцируя первое уравнение системы, имеем откуда, используя второе уравнение, получаем — линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией.
Его общее решение имеет вид . В силу первого уравнения системы находим функцию . Найденные функции x(t), y(t), как легко проверить, при любых значениях С| и С2 удовлетворяют заданной системе. Функции можно представить в виде откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом с общей осью х = у = 0, которая также является интегральной кривой (рис. 3). Исключая в формулах (7) параметр получаем уравнение так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость.
При Л=0 фазовая траектория состоит из одной точки , называемой точкой покоя системы. ». Может оказаться, что функции нельзя выразить через Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений нельзя заменить эквивалентным уравнением второго порядка относительно х\ или х2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает Метод интегрируемых комбинаций Интегрирование нормальных систем дифференциальных уравнений dXi иногда осуществляется методом интегрируемых комбинаций.
Возможно вам будут полезны данные страницы:
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся. Пример.
Методы интегрирования
Метод исключения Метод интегрируемых комбинаций Системы линейных дифференциальных уравнений Фундаментальная матрица Метод вариации постоянных Системы линейных дифференциальных уравнений с постоянными коэффициентами Матричный метод 4 Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию: откуда Мы нашли два конечных уравнения з которых легко определяется общее решение системы: Одна интегрируемая комбинация дает возможность получить одно уравнение связывающее независимую переменную t и неизвестные функции . Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.
| Если найдено п первых интегралов |
системы (8) и все они независимы, т. е. якобиан системы функций отличен от нуля: Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система п линейных уравнений первого порядка, записанная в нормальной форме, имеет вид или, в матричной форме, Теорема 2.
Если все функции , непрерывны на отрезке , то в достаточно малой окрестности каждой точки ., хп),где ), выполнены условия теоремы существования и единственности решения задачи Кошии, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t)x\,x2>. ,хп и их частные производные по , ограничены, так как эти производные равны непрерывным на отрезке [a, Ь] коэффициентам Введем линейный оператор Тогда система (2) запишется в виде Если матрица F — нулевая, на интервале (а, 6), то система (2) называется линейной однородной и имеет вид Приведем некоторые теоремы, устанавливающие свойства решений линейных си- стем. Теорема 3. Если X(t) является решением линейной однородной системы где с — произвольная постоянная, является решением той же системы. Теорема 4.
Сумма двух решений однородной линейной системы уравнений является решением той же системы. Следствие. Линейная комбинация с произвольными постоянными коэффициентами с, решений линейной однородной системы дифференциальных уравнений является решением той же системы. Теорема 5. Если X(t) есть решение линейной неоднородной системы — решение соответствующей однородной системы то сумма будет решением неоднородной системы.
Действительно, по условию, Пользуясь свойством аддитивности оператора получаем Это означает, что сумма есть решение неоднородной системы уравнений Определение. Векторы где называются линейно зависимыми на интервале , если существуют постоянные числа такие, что при , причем по крайней мере одно из чисел а, не равно нулю. Если тождество (5) справедливо только при то векторы называются линейно независимыми на (а, Ь). Заметим, что одно векторное тождество (5) эквивалентно п тождествам: . Определитель называется определителем Вронского системы векторов . Определение.
Пусть имеем линейную однородную систему где -матрица с элементами Система п решений линейной однородной системы (6), линейно независимых на интервале , называется фундаментальной. Теорема 6. Определитель Вронского W(t) фундаментальной на интервале системы решений линейной однородной системы (6) с непрерывными на отрезке а b коэффициентами a-ij Общим решением в области линейной однородной системы с непрерывными на отрезке коэффициентами является линейная комбинация п линейно независимых на интервале а решений системы (6): произвольные постоянные числа). Пример. Система имеет, как нетрудно проверить, решения Эш решения линейно независимы, так как определитель Вронского отличен от нуля: ‘ Общее решение системы имеет вид или — произвольные постоянные). 3.1. Квадратная матрица столбцами которой являются линейно независимые решения системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению Если X(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде — постоянная матрица-столбец с произвольными элементами. Полагая в имеем откуда следовательно, Матрица называется матрицей Коши. С ее помощью решение системы (6) можно представить так: Теорема 8 (о структуре общего решения линейной неоднородной системы дифференциальных уравнений). Общее решение в области линейной неоднородной системы дифференциальных уравнений с непрерывными на отрезке коэффициентами и правыми частями fi(t) равно сумме общего решения соответствующей однородной системы и какого-нибудь частного решения X(t) неоднородной системы (2): 3.2. Метод вариации постоянных Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лаг-ранжа). Пусть есть общее решение однородной системы (6), тогда dXk причем решения линейно независимы. Будем искать частное решение неоднородной системы где — неизвестные функции от t. Дифференцируя имеем Подставляя получаем Так как то для определения получаем систему или, в развернутом виде, Система (10) есть линейная алгебраическая система относительно 4(0 > определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале так что система ) имеет единственное решение где МО — известные непрерывные функции. Интегрируя последние соотношения, находим Подставляя эти значения , находим частное решение системы (2): (здесь под символом понимается одна из первообразных для функции §4. Системы линейных дифференциальных уравнений с постоянными коэффициентами Рассмотрим линейную систему дифференциальных уравнений в которой все коэффициенты — постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа. Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем. Метод Эйлера Будем искать решение системы где — постоянные. Подставляя ж* в форме (2) в систему (1), сокращая на е* и перенося все члены в одну часть равенства, получаем систему Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с п неизвестными ап имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю: Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно А степени п. Из этого уравнения определяются те значения А, при которых система (3) имеет нетривиальные решения а\, Если все корни характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения , этой системы и, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1) образуют, как можно проверить, фундаментальную систему решений этой системы. Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид — произвольные постоянные. Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем. М Ищем решение в виде Характеристическое уравнение Система (3) для определения 01,02 выглядит так: Подставляя получаем откуда Следовательно, Полагая находим поэтому Общее решение данной системы: Метод исключения Метод интегрируемых комбинаций Системы линейных дифференциальных уравнений Фундаментальная матрица Метод вариации постоянных Системы линейных дифференциальных уравнений с постоянными коэффициентами Матричный метод Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде матрица с постоянными действительными элементами a,j. Напомним некоторые понятия из линейной алгебры. Вектор g Ф О называется собственным вектором матрицы А, если Число А называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения где I — единичная матрица. Будем предполагать, что все собственные значения А„ матрицы А различны. В этом случае собственные векторы линейно независимы и существует п х п-матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что Столбцами матрицы Т являются координаты собственных векторов Введем еще следующие понятия. Пусть В(£) — п х n-матрица, элементы 6,;(0 которой суть функции аргумента t, определенные на множестве Матрица B(f) называется непрерывной на П, если непрерывны на Q все ее элементы 6,j(f). Матрица В(*) называется дифференцируемой на П, если дифференцируемы на Q все элементы этой матрицы. При этом производной ^р- матрицы В(*) называется матрица, элементами которой являются производные —соответствующих элементов матрицы В(*). Пусть B — вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы В частности, если В — постоянная матрица, то так как ^ есть нуль-матрица. Теорема 9. Если собственные значения матрицы А различны, то общее решение системы (7) имеет вид где — собственные векторы-столбцы матрицы произвольные постоянные числа. Введем новый неизвестный вектор-столбец по формуле где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя получим систему Умножая обе части последнего соотношения слева на Т 1 и учитывая, что Т 1 AT = Л, придем к системе Мы получили систему из п независимых уравнений, которая без труда интегрируется: (12) Здесь — произвольные постоянные числа. Вводя единичные п-мерные векторы-столбцы решение можно представить в виде Так как столбцы матрицы Т есть собственные векторы матрицы собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10): Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы: 1) находим собственные значения „ матрицы как корни алгебраического уравнения 2) находим все собственные векторы 3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10). Пример 2. Решить систему Матричный метод 4 Матрица А системы имеет вид 1) Составляем характеристическое уравнение Корни характеристического уравнения . 2) Находим собственные векторы Для А = 4 получаем систему откуда = 0|2, так что Аналогично для А = 1 находим I 3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты ау системы (7) действительные, то характеристическое уравнение будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем А оно будет иметь и корень \*, комплексно сопряженный с А. Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению А, то А* — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g. При комплексном Л решение системы (7) taioKe будет комплексным. Действительная часть и мнимая часть этого решения являются решениями системы (7). Собственному значению Л* будет отвечать пара действительных решений . та же пара, что и для собственного значения Л. Таким образом, паре А, А* комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений. Пусть — действительные собственные значения, комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид где с, — произвольные постоянные. Пример 3. Решить систему -4 Матрица системы 1) Характеристическое уравнение системы Его корни Собственные векторы матрицы 3) Решение системы где — произвольные комплексные постоянные. Найдем действительные решения системы. Пользуясь формулой Эйлера получаем Следовательно, всякое действительное решение системы имеет вид произвольные действительные числа. Упражнения Методом исключения проинтегрируйте системы: Методом интефируемых комбинаций проинтефируйте системы: Матричным способом проинтефируйте системы: Ответы Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги. http://lfirmal.com/ponyatie-o-sistemah-differencialnyh-uravnenij/ http://natalibrilenova.ru/sistemyi-differentsialnyih-uravnenij-metodyi-integrirovaniya-metod-isklyucheniya/Фундаментальная матрица
Методы интегрирования