Методы оценивания параметров уравнения регрессии

Оценка параметров уравнения регреcсии. Пример

Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x β ;
y = α β x ;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.

Требуется:
1. Построить уравнения парной регрессии y от x :

• линейное;
• степенное;
• показательное;
• равносторонней гиперболы.

2. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы.
3. Оценить статистическую значимость уравнения регрессии в целом.
4. Оценить статистическую значимость параметров регрессии и корреляции.
5. Выполнить прогноз затрат на производство при прогнозном выпуске продукции, составляющем 195 % от среднего уровня.
6. Оценить точность прогноза, рассчитать ошибку прогноза и его доверительный интервал.
7. Оценить модель через среднюю ошибку аппроксимации.

1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения

Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии

Коэффициент детерминации
R 2 =0.94 2 = 0.89, т.е. в 88.9774 % случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19
y(2) = 4.01*2 + 99.18 = 107.2
. . .

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;α/2) = (11;0.05/2) = 1.796
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.

Анализ точности определения оценок коэффициентов регрессии

S a = 0.1712
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается

Статистическая значимость коэффициента регрессии b не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (t_табл=1.796):
(a — t_табл·S_a; a + t_табл·S a)
(1.306;1.921)
(b — t_табл·S b; b + t_табл·S_b)
(-9.2733;41.876)
где t = 1.796
2) F-статистики

Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим

Оценка параметров линейного регрессионного уравнения

Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов (МНК), в основе которого лежит предположение о независимости наблюдений исследуемой совокупности. Сущность данного метода заключается в нахождении параметров модели (α, β), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:

В итоге получаем систему нормальных уравнений:

Эту систему можно записать в виде:

_{Решая данную систему линейных уравнений с двумя неизвестными получаем оценки наименьших квадратов:}

_{В уравнениях регрессии параметр α показывает усредненное влияние на результативный признак неучтенных факторов, а параметр β – коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу.}

_{Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:}

_{где – коэффициент регрессии в уравнении связи;}

– среднее квадратическое отклонение соответствующего статистически существенного факторного признака.

_{Имеются следующие данные о размере страховой суммы и страховых возмещений на автотранспортные средства одной из страховых компаний.}

_{Зависимость между размером страховых возмещений и страховой суммой на автотранспорт}

_{Объем страхового возмещения (тыс.долл.), Yi}

_{Стоимость застрахованного автомобиля (тыс.долл.), X i}

Оценка параметров регрессионной модели

ГЛАВА 3. МОДЕЛЬ МНОЖЕСТВЕННОЙ

ЛИНЕЙНОЙ РЕГРЕССИИ

Основные понятия и уравнения множественной регрессии

На любой экономический показатель чаще всего оказывает влияние не один, а несколько совокупно действующих факторов. Например, объем реализации (Y) для предприятий оптовой торговли может определяться уровнем цен (Х₁), числом видов товаров (Х₂), размером торговой площади (Х₃) и товарных запасов (Х₄). В целом объем спроса на какой-либо товар определяется не только его ценой (Х₁), но и ценой на конкурирующие товары (Х₂), располагаемым доходом потребителей (Х₃), а также некоторыми другими факторами. Показатель инновационной активности современных предприятий зависит от затрат на исследования и разработки (Х₁), на приобретение новых технологий (Х₂), на приобретение программных продуктов и средств (Х₃) и обучение и переподготовку кадров [7,28]. В этих случаях возникает необходимость рассмотрения моделей множественной (многофакторной, многомерной) регрессии [28].

Модель множественной линейной регрессии является естественным обобщением парной (однофакторной) линейной регрессионной модели. В общем случае ее теоретическое уравнение имеет вид:

(3.1)

где Х₁, Х₂,…, Х_m – набор независимых переменных (факторов-аргументов); b₀, b₁, …, b_m – набор (m + 1) параметров модели, подлежащих определению; ε – случайное отклонение (ошибка); Y – зависимая (объясняемая) переменная.

Для индивидуального i-го наблюдения (i = 1, 2, …, n) имеем:

(3.2)

. (3.3)

Здесь b_j называется j—м теоретическим коэффициентом регрессии (частичным коэффициентом регрессии).

Аналогично случаю парной регрессии, истинные значения параметров (коэффициентов) b_j по выборочным данным получить невозможно. Поэтому для определения статистической взаимосвязи переменных Y и Х₁, Х₂, …, Х_m оценивается эмпирическое уравнение множественной регрессионной модели

(3.4)

в котором , – оценки соответствующих теоретических коэффициентов регрессии; е – оценка случайного отклонения ε.

Оцененное уравнение (3.4) в первую очередь должно описывать общий тренд (направление, тенденцию) изменения зависимой переменной Y. При этом необходимо иметь возможность рассчитать отклонения от этого тренда.

Для решения задачи определения оценок параметров множественной линейной регрессии по выборке объема n необходимо выполнение неравенства n ³ m + 1 (m – число регрессоров). В данном случае число v = n — m — 1 будет называться числом степеней свободы. Отсюда для парной регрессии имеем v = n — 2. Нетрудно заметить, что если число степеней свободы невелико, то и статистическая надежность оцениваемой формулы невысока. На практике принято считать, что достаточная надежность обеспечивается в том случае, когда число наблюдений по крайней мере в три раза превосходит число оцениваемых параметров k = m + 1. Обычно, статистическая значимость парной модели наблюдается при n ≥ 7.

Самым распространенным методом оценки параметров уравнения множественной линейной регрессионной модели является метод наименьших квадратов (МНК). Напомним (см. раздел 2.4.1), что надежность оценок и статистических выводов, полученных с использованием МНК, обеспечивается при выполнении предпосылок Гаусса-Маркова. В случае множественной линейной регрессии к предпосылкам 1–4 необходимо добавить еще одну (пятую) – отсутствие мультиколлинеарности, что означает отсутствие линейной зависимости между объясняющими переменными в функциональной или статистической форме. Более подробно мультиколлинеарность объясняющих переменных будет рассмотрена в разделе (3.4). Модель, удовлетворяющая предпосылкам МНК, называется классической нормальной моделью множественной регрессии.

На практике часто бывает необходимо оценить силу влияния на зависимую переменную различных объясняющих (факторных) переменных. В этом случае используют стандартизованные коэффициенты регрессии и средние коэффициенты эластичности .

Стандартизированный коэффициент регрессии определяется по формуле:

(3.5)

где S(x_j) и S(y) – выборочные средние квадратичные отклонения (стандарты) соответствующей объясняющей и зависимой переменных.

Средний коэффициент эластичности

(3.6)

показывает, на сколько процентов (от средней) изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на 1 %.

Для модели с двумя объясняющими (факторными) переменными , после нахождения оценок , уравнение определяет плоскость в трехмерном пространстве. В общем случае m независимых переменных геометрической интерпретацией модели является гиперплоскость в гиперпространстве.

Оценка параметров регрессионной модели

Для нахождения оценок параметров b_j множественной линейной регрессионной модели (коэффициентов эмпирического уравнения регрессии) используется метод наименьших квадратов (МНК). Суть МНК заключается в минимизации суммы квадратов отклонений наблюдаемых выборочных значений y_i зависимой переменной Y от их модельных оценок . Отклонение е_i, соответствующее уравнению регрессии в i-м наблюдении (i = 1, 2, …, n), рассчитывается по формуле:

. (3.7)

Тогда для нахождения коэффициентов 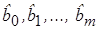по МНК минимизируется следующая функция m + 1 переменных:

. (3.8)

Необходимым условием минимума функции G является равенство нулю всех ее частных производных по Частные производные квадратичной функции (3.8) являются линейными функциями относительно параметров:

. (3.9)

Приравнивая (3.9) к нулю, получаем систему m + 1 линейных нормальных уравнений с m + 1 неизвестными для определения параметров модели:

(3.10)

где j = 1, 2, …, m – определяет набор регрессоров.

Следует заметить, что включение в модель новых объясняющих переменных усложняет расчет коэффициентов множественной линейной регрессии путем решения системы (3.10) по сравнению с парной моделью. Система из трех уравнений, соответствующая модели с двумя объясняющими переменными , может быть легко решена методом определителей. Однако в общем виде решение системы (3.10) и анализ множественной регрессионной модели наиболее целесообразно проводить в векторно-матричной форме [15,17].

Тогда, вводя матричные обозначения, запишем:

, , .

Здесь Y – n-мерный вектор-столбец наблюдений зависимой переменной; Х – матрица размерности n · (m + 1) значений объясняющих переменных x_ij, в которой единица соответствует переменной при свободном члене ; – вектор-столбец размерности m + 1 оценок параметров модели (коэффициентов уравнения регрессии); е – вектор-столбец размерности n отклонений выборочных (реальных) значений y_i зависимой переменной, от значений оценок , получаемых по уравнению регрессии.

В матричной форме модель (3.1) примет вид:

Оценкой этой модели по выборочным данным является уравнение (эмпирическая модель)

. (3.12)

Предпосылки МНК (см. раздел 2.4.1.) в матричной форме можно записать следующим образом:

1. M(e) = 0; 2. D(e) = σ 2 I; 3. Матрица ковариаций V(e) = M(e · e T ) = σ 2 E,

где e = – вектор-столбец случайных отклонений (ошибок);

I = – (n · 1) вектор;

E = E_n×n = – единичная матрица;

– матрица ковариаций или ковариационная матрица вектора случайных отклонений, которая является многомерным аналогом дисперсии одной переменной и в которой, если предпосылка о некоррелированности отклонений e_i и e_j выполняется, все элементы, не лежащие на главной диагонали, равны нулю, а элементы главной диагонали равны одной и той же дисперсии D(e_i) = σ 2 ; 4. e – нормально распределенный случайный вектор, т. е. e

N(0, σ 2 Е); 5. r(X) = m + 1 > n – детерминированная матрица объясняющих переменных (регрессоров) имеет ранг r, равный числу определяемых параметров модели m + 1, кроме того, число имеющихся наблюдений каждой из объясняющих переменных и зависимой переменной превосходит ранг матрицы Х.

Выполнение пятой предпосылки означает линейную независимость объясняющих переменных (линейную независимость столбцов матрицы Х), т. е. отсутствие функциональной мультиколлинеарности.

Наша задача заключается в нахождении вектора оценок по МНК, который, при выполнении предпосылок 1–5, обладает наименьшим рассеянием относительно параметра B.

Воспользовавшись известными соотношениями матричной алгебры и правилами дифференцирования по векторному аргументу, получим необходимое условие минимума функции G (равенство нулю вектор-столбца частных производных )

(3.13)

откуда вытекает система нормальных уравнений в матричной форме для определения вектора

(3.14)

где Х Т – транспонированная матрица.

Решением уравнения (3.14) является вектор оценок:

(3.15)

где (Х Т Х) — 1 – матрица, обратная Х Т Х; Х Т Y – вектор-столбец свободных членов системы.

Найдем матрицы, входящие в матричное уравнение (3.14):

. (3.16)

Матрица Х Т Х образует симметричную матрицу сумм первых степеней, квадратов и попарных произведений n наблюдений объясняющих переменных.

. (3.17)

Матрица Х Т Х представляет вектор-столбец произведений n наблюдений объясняющих и зависимой переменных.

Зная вектор коэффициентов множественной линейной регрессии (3.15), находим оценку (групповую среднюю) зависимой переменной Y при заданном векторе значений объясняющей (факторной) переменной [11,28].

Пример 3.1. Для иллюстрации получим формулы для расчета коэффициентов парной регрессии (m = 1), используя матричные обозначения.

В соответствии с (3.17) определим матрицу А — 1 = (Х Т Х) — 1 по формуле:

,

где detA – определитель матрицы Х Т Х; A * – присоединенная матрица (транспонированная матрица алгебраических дополнений).

Для данного примера:

.

, .

.

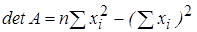
Тогда вектор оценок для частного случая m = 1 определяется как:

,

откуда следуют формулы (2.11) для определения параметров парной регрессионной модели.