Методы решение логарифмических показательных уравнениях

Применение нестандартных способов при решении показательных и логарифмических уравнений и неравенств

Разделы: Математика

Цель урока:

1. систематизировать знания о некоторых нестандартных способах решения, умение применять свойства функций, правила при решении уравнений и неравенств;
2. развивать умение видеть, умение распознавать рациональность применения того или иного способа;
3. прививать интерес к математике, воспитывать математическую грамотность ученика, как при устной, так и при письменной работе.

Оборудование: компьютер, мультимедийный проектор, экран.

План урока:

1. Орг. момент.
2. Устная работа.
3. Работа в группах
4. Защита решений.
5. Сам. работа.
6. Задание на дом
7. Итог урока.

Ход урока

I. Организационный момент.

• знакомство с целью урока; задачами, стоящими перед учениками в ходе уроке.
• использование при решении задач:
  – монотонности функций;
  – «правила знаков»;
  – метода оценки;
  – освобождение от логарифма.

II. Устная работа.

1. Какие из выражений имеют смысл?

а)	а) да;
б)	б) нет, т.к.
в)	в) нет, т.к. а
г)	г) да;
д)	д) нет, т.к.

2. Решить уравнение:

(Корень уравнения угадываем: х = 1. Докажем, что других корней нет. Левая часть – сумма возрастающих функций есть функция возрастающая; правая часть – постоянное число. Следовательно, уравнение имеет одно решение.)

3. Решить уравнение:

/ :

(Корень уравнения угадываем: х = 2. Докажем, что других корней нет.

Разделим обе части уравнения на

следовательно, в левой части уравнения – сумма двух убывающих показательных функций, правая часть – const. Следовательно, уравнение имеет одно решение.)

– Какое свойство функций мы использовали при решении этих уравнений?

III. Работа в группах. Решение задач.

1 группа. Решить уравнение:

– Какой способ надо применить при решении данного уравнения?

– Используем свойство монотонности убывающей функции, для этого разделим на

– Можем ли мы угадать хоть один корень?

(Можно угадать корень уравнения: х = 2.)

В левой части – сумма убывающих функций, в правой части – const. Следовательно, левая и правая части имеют одну точку пересечения:

точка пересечения, х=2.

значит, уравнение имеет одно решение,

2 группа. Решить неравенство:

– Применим теорему для функции f(f(x)).

Если функция у = f(x) – монотонно возрастающая функция, то уравнение f(x)=x равносильно f(f(x)= x.

ОДЗ:

– Выполним некоторые преобразования:

– вынесем в левой части за скобки 2, сократим:

– приведем к общему знаменателю:

т.к. , а , тогда

функция принимает вид , где — возрастающая функция, следовательно, по теореме имеем:

– Учитывая ОДЗ, получим:

3 группа. Решить неравенство:

– Решим неравенство методом оценки левой и правой частей

;

–Заметим, что .

;

– Разделим обе части уравнения на положительное выражение , получим:

;

– Выделим полный квадрат под радикалом и в показателе степени:

– Левая часть неравенства не меньше 1, а правая часть не больше 1.

– Неравенство выполняется тогда и только тогда, когда обе части неравенства будут равны 1, а равенство достигается при х = 3.

4 группа. Решить уравнение:

;

– Решим уравнение методом оценки;

– Один корень уравнения можно легко угадать, это х = 1.

– Преобразуем логарифмы в левой части;

;

;

Выделим полный квадрат в правой части;

– Правая часть меньше или равна 1;

наибольшее значение правой части равно 1 при х=1;

– В левой части докажем, что выражение под знаком логарифма больше или равно 2: подведением под общую дробную черту, выделением полного квадрата

– левая часть достигает своего наименьшего значения, равного 1 при х = 1.

– Равенство выполняется тогда и только тогда, когда обе части уравнения равны 1, а это произойдет при х = 1.

5 группа. Решить неравенство:

– Решим неравенство методом освобождения от логарифмов.

– Освободимся от логарифмов по правилу знаков:

Знак log a b совпадает со знаком произведения (а – 1)∙(в – 1).

Решение: Т.к. нас интересует только знак левой части, то от можно логарифмов освободиться по правилу знаков:

– Решим неравенство методом интервалов, рассмотрим функцию f(x):

найдем нули функции: нули функции

функция f(x) > 0 при учитывая ОДЗ, получим:

Ответ:

IV. Защита проектов.

– От каждой группы выступает 1 человек с защитой своего решения (решение на доске кратко записать, пояснения по ходу решения, либо записать на ватмане).

V. Самостоятельная работа.

– Проверим решение уравнений по готовым записям на доске:

Методы решения показательных и логарифмических уравнений

Тема занятия: Методы решения показательных и логарифмических уравнений

Тип занятия: обобщение и систематизация знаний и способов действий в сочетании с их комплексным применением

Цели занятия:

1. Образовательные:

— создать условия для повторения и обобщения знаний учащихся по теме «Решение логарифмических уравнений и неравенств»;

— активизировать деятельность учащихся по применению комплекса знаний и умений на практике;

— подготовка к ЕГЭ.

2. Развивающие:

— развивать способности применять теоретические знания на практике;

— развивать навыки работы с заданиями № 5 базового уровня ; № 13 профильного уровня

— развивать навыки самоконтроля , логическое мышление, память, внимание.

3. Воспитательные:

— воспитывать ответственное отношение к изучению математики, трудолюбие, взаимопомощь, волю и настойчивость в достижении поставленной цели.

Оборудование урока: презентация, компьютер, проектор, карточки с заданиями, диагностические карты.

Просмотр содержимого документа
«Методы решения показательных и логарифмических уравнений»

Тема занятия: Методы решения показательных и логарифмических уравнений

Тип занятия: обобщение и систематизация знаний и способов действий в сочетании с их комплексным применением

— создать условия для повторения и обобщения знаний учащихся по теме «Решение логарифмических уравнений и неравенств»;

— активизировать деятельность учащихся по применению комплекса знаний и умений на практике;

— подготовка к ЕГЭ.

— развивать способности применять теоретические знания на практике;

— развивать навыки работы с заданиями № 5 базового уровня ; № 13 профильного уровня

— развивать навыки самоконтроля , логическое мышление, память, внимание.

— воспитывать ответственное отношение к изучению математики, трудолюбие, взаимопомощь, волю и настойчивость в достижении поставленной цели.

Оборудование урока: презентация, компьютер, проектор, карточки с заданиями, диагностические карты.

Организация начала занятия (Приветствие, объявляю тему и цель занятия)

Девиз сегодняшнего занятия звучит так: «Математика, друзья, абсолютно всем нужна. На уроках работай старательно, и успех тебя ждёт обязательно

Только твой труд при изучении математики может принести плоды. На сегодняшнем занятии перед нами стоит задача: повторить основные типы показательных и логарифмических уравнений и методы их решения. Знания, полученные вами при изучении темы, должны дать положительные результаты при выполнении подобных заданий в тестовой работе ЕГЭ.

Каждый из вас сегодня оценит свои знания по теме, постарается понять, где имеются пробелы.

Итак, мы начинаем.

Актуализация знаний обучающихся

Формулы Свойства степени;

Формулы Свойства логарифмов;

Фронтальная работа с классом:

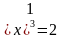
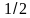
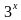
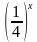
Вычислить: 2) = 3 ) = 81 4) =6 5) = 3

6) ; ; 8)

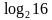
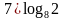
Проверяем ответы по формулам у доски: по одному ученику каждый вид формул (работа экспертов), затем сверяем ответы по слайду.

Далее – графический диктант по свойствам логарифмической и показательной функций

Согласны-:Λ, не согласны :_

1.Функцию вида у=а х, где а0 и а≠1, называют показательной функцией.

2.Областью определения логарифмической функции является вся числовая прямая.

3.Областью значений показательной функции является промежуток (0;+∞).

4.Логарифмическая функция при а1 является убывающей.

5.Функцию вида у = log _а х называют логарифмической функцией.

6.Областью определения показательной функции является вся числовая прямая.

7.Областью значений логарифмической функции является промежуток (-∞;+∞).

8.Показательная функция при 0

Проверяем: С какими высказываниями вы не согласны и почему. Сверяем правильность ответов с презентацией.

Комплексное применение знаний на практике

Свойства логарифмической и показательной функций используем на практике при решении уравнений

Простейшие показательные уравнения имеют вид:

= , которые равносильны уравнению

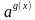
f(x)=g(x). Такое уравнение может встретиться в КИМах ЕГЭ в задании №5

=b – логарифмируем левую и правую части уравнения по основанию a:

и решаем дальше

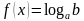
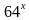
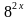
Пример: решить уравнение = ( у доски решает ученик),

= ; 9-х=2х; -3х=-9; х=3.

Пример: решить уравнение

=3;

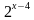
х-4= ;

х=4+ = + = ; —

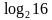
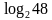
решают на закрытой части доски, затем открываем и проверяем с классом;

Простейшие логарифмические уравнения:

= при выполнении условий:

=c, f(x)= по определению логарифма.

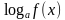
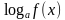
2) = ; 15+х=3; х=3-15; х=3.

— на закрытой доске с последующей проверкой

Проверяем навыки применения методов решения простейших уравнений на практике –

Алгебра

План урока:

Задание. Укажите корень логарифмического уравнения

Задание. Решите урав-ние

В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид

Задание. Найдите решение логарифмического уравнения

Задание. Решите урав-ние

Задание. Решите урав-ние

Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:

Уравнения вида log_af(x) = log_ag(x)

Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.

Задание. Решите урав-ние

Задание. Найдите корень урав-ния

Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид

С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.

Задание. Решите урав-ние

Получили квадратное уравнение, которое решаем с помощью дискриминанта:

Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:

Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:

Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log₃ (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).

Уравнения, требующие предварительных преобразований

Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду log_af(x) = log_ag(x).

Задание. Решите урав-ние

с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:

Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:

Задание. Решите урав-ние

Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем

Задание. Решите урав-ние

Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log₅ 5. Тогда урав-ние можно преобразовать:

Задание. Решите урав-ние

Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что

Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что

Задание. Решите урав-ние

Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log₂₅x 4 к основанию 5, используя известную нам формулу

Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:

Логарифмические уравнения с заменой переменных

Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.

Задание. Решите уравнение методом замены переменной

Задание. Найдите решение уравнения методом замены переменной

Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:

Логарифмирование уравнений

Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.

Задание. Укажите корни урав-ния

Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:

Возвращаемся от переменной t к переменной х:

Переход от логарифмических неравенств к нелогарифмическим

Рассмотрим график логарифмической функции у = log_ax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства

Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.

Задание. Найдите решение логарифмического неравенства

Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 log_as:

Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 log_a s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение

Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:

Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).