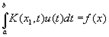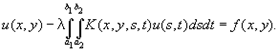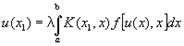Методы решения интегро дифференциальных уравнений

Приближённые методы решения интегро-дифференциальных уравнений Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Ахмадиев М.Г., Хасанов Ю.Х.

В работе для численного решения сингулярного интегро-дифференциального уравнения задачи дифракции используется метод механических квадратур . Доказано, что этот метод устойчив относительно малых возмущений элементов аппроксимирующих уравнений .

Похожие темы научных работ по математике , автор научной работы — Ахмадиев М.Г., Хасанов Ю.Х.

Drawn near methods of the decision integro-differential equations

In work for the numerical decision singular integro-differential equations of the problem diffraction is used method of the mechanical squarings. It is proved that this method is stable for small indignations element aproximating equations .

Текст научной работы на тему «Приближённые методы решения интегро-дифференциальных уравнений»

ДОКЛАДЫ АКАДЕМИИ НАУК РЕСПУБЛИКИ ТАДЖИКИСТАН _2015, том 58, №3_

ПРИБЛИЖЁННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Казанский химико-технологический университет, Россия, Российско-Таджикский (Славянский) университет

(Представлено членом корреспондентом АН Республики Таджикистан З.Х.Рахмоновым 10.07.2014 г.)

В работе для численного решения сингулярного интегро-дифференциального уравнения задачи дифракции используется метод механических квадратур. Доказано, что этот метод устойчив относительно малых возмущений элементов аппроксимирующих уравнений.

Ключевые слова: приближенные методы — задача дифракции — метод механических квадратур -сингулярные интегро-дифференциальные уравнения — аппроксимирующие уравнения — операторные уравнения.

В работах 6 рассмотрены прямые методы решения следующего уравнения теории крыла

B(t)Г(Г) — — f ^^ dt = f (t), -1 1т=/(,). — 1 /1 — Г с

обычной нормой. Через обозначим пространство функций, удовлетворяющих условиям (2), пер-

вые производные которых квадратично-суммируемы с весом р(г)

Пусть X = ^р, У = Ь2 . Тогда задачу (1)-(2) запишем в виде операторного уравнения, эквивалентного ей

Кр = 8р + Тр = /, реX, / еУ, (6)

р Л | РР\1 \ Тр = | ^-\рр(т)Лт. т — г г — т

Теорема. Пусть / е С, И(г, т) непрерывна по переменному г и удовлетворяет условию Ди-ни-Липшица по переменной т и уравнение (6) однозначно разрешимо в X при любой правой части / еУ. Тогда при п таких, что

1п п !> Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

\\KVn — К(Р„12р=\\ТкРп — РпТРпт(кРп)

Замечание 1. Так как в условиях теоремы операторы Ки линейно обратимы и обратные ограничены по норме в совокупности, то из результатов работы [10] (см. §5 главы 1) следует, что рассмотренный нами метод устойчив относительно малых возмущений элементов аппроксимирующих уравнений.

Замечание 2. Поскольку в условиях теоремы существует число обусловленности ] = ]](К) для точного уравнения (6), то из результатов работы [10] (см. §5 главы 1) следует, что в условиях теоремы хотя бы при достаточно больших п существуют число обусловленности ] = ]](Кп) для аппроксимирующих уравнений (61), причём

т]п 0, п > п0(е)\ Иш]п=].

Поступило 12.07.2014 г.

1. Каландия А.И. Математические методы двумерной теории упругости. — М.: Наука, 1973.

2. Габдулхаев Б.Г. — Изв. вузов. Матем., 1974, №2, с. 29-44.

3. Иванов В.В. Теория приближенных методов и ее применение к численному решению сингулярных интегральных уравнений. — Киев: Наукова думка, 1968.

4. Габдулхаев Б.Г. — Итоги науки и техники. Серия Математика. — М.: ВИНИТИ, 1980, т.18, с.251-307.

5. Ioakimidis N.I. — Int.j. Meth. Fluids, 1984, 4, № 3, рр.283-290.

6. Белоцерковский С.М., Лифанов И.К. Численные методы в сингулярных интегральных уравнениях и их применение в аэродинамике, теории упругости, электродинамике. — М.: Наука, 1985.

7. Захаров Е.В., Собянина И.В. — Журн. выч. матем. и матем. физ. 1986, т. 26, №4, с.632-636.

8. Панасюк В.В., Саврук М.П., Назарчук З.Т. Метод сингулярных интегральных уравнений в двумерных задачах дифракции. — Киев: Наукова думка, 1984.

9. Ахмадиев М.Г. — Прямые методы решения некоторых сингулярных интегро-дифференциальных уравнений. Казан. ун-т. Казань, 1986, 18 с. Деп. в ВИНИТИ 02.01.86, № 43-В.

10. Габдулхаев Б.Г. Оптимальные аппроксимации решений линейных задач. — Казань: Изд-во КГУ, 1980.

11. Натансон П.Н. Конструктивная теория функций. — М.-Л.: Гостехиздат, 1949.

УСУЛ^ОИ ТАЦРИБИИ ^АЛЛИ МУОДИЛА^ОИ ИНТЕГРО-ДИФФЕРЕНЦИАЛЙ

Донишго^и химико-технологии Казон, *Донишго%и (Славянии) Россияю Тоцикистон

Дар макола барои хдлли такрибии муодилах,ои сингулярии интегро-дифференциалии масъалаи дифракция усули квадратураи механикй истифода карда шудааст. Устувории ин усул нисбати тамоили хурдтарини элементх,ои муодилах,ои аппроксимативй нишон дода мешавад. Калима^ои калиди: усулуои тацрибй — масъалаи дифраксия — усули квадратураи механики -муодилауои синулярии интегро-дифференсиалй — муодилауои аппроксимативй — муодилауои операторй.

M.G.Akhmadiev, Yu.Kh.Khasanov* DRAWN NEAR METHODS OF THE DECISION INTEGRO-DIFFERENTIAL

Kazan chemist-technology University, Russian-Tajik (Slavonic) University In work for the numerical decision singular integro-differential equations of the problem diffraction is used method of the mechanical squarings. It is proved that this method is stable for small indignations element aproximating equations.

Key words: approximate methods — diffraction problem — method of the mechanical squaring — singular and integro-differential equations — aproximating equations — operators equations.

Интегро-дифференциальные уравнения

Ряд задач математической физики приводит к интегральным уравнениям различных типов. Так, например, интегральные уравнения Вольтерра возникают в тех задачах физики, в которых существует предпочтительное направление изменения независимого переменного (например, времени, энергии и т.д.). В задаче о крутильных колебаниях возникает некоторое интегро-дифференциальное уравнение.

Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У. м. ф. много усилий было затрачено на отыскание их общего решения. Уже Ж. Д’Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л. Эйлером (1770), П. Лаплас предложил (1773) «каскадный метод», дающий общее решение некоторых др. линейных однородных гиперболических уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значительного класса уравнений, для которых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось, что при анализе физических процессов У. м. ф. обычно появляются вместе с дополнительными условиями, характер которых коренным образом влияет на направление исследования.

Широкое распространение получили методы приближённого решения краевых задач, в которых задача сводится к решению системы алгебраических (обычно линейных) уравнений. При этом за счёт увеличения числа неизвестных в системе можно достичь любой степени точности приближения.

Интегро-дифференциальные уравнения, уравнения, содержащие неизвестную функцию под знаком интеграла и под знаком производной. Например, уравнение, полученное итальянским математиком В. Вольтерра в задаче о крутильных колебаниях:

Иногда интегро-дифференциальные уравнения можно свести к интегральным уравнениям или дифференциальным уравнениям. Решение интегро-дифференциальных уравнений можно искать по методу последовательных приближений[4].

Интегральные уравнения, уравнения, содержащие неизвестные функции под знаком интеграла. Многочисленные задачи физики и математической физики приводят к интегральным уравнениям различных типов. Пусть, например, требуется с помощью некоторого оптического прибора получить изображение линейного объекта А, занимающего отрезок 0 £ x £ l оси Ox, причём освещённость объекта характеризуется плотностью u(x). Изображение В представляет собой некоторый отрезок другой оси x₁; последний путём подходящего выбора начала отсчёта и единицы длины также можно совместить с отрезком 0 £ x₁ £ l . Если дифференциально малый участок (х, х + Dх) объекта А вызывает освещённость изображения В с плотностью K(x₁, x)u(x)dx, где функция K(x₁, x) определяется свойствами оптического прибора, то полная освещённость изображения будет иметь плотность

В зависимости от того, хотят ли добиться заданной освещённости v(x₁) изображения или «точного» фотографического изображения [v(x) = ku(x), где постоянная k заранее не фиксируется], или, наконец, определённой разницы освещённости А и В [u(x) — v(x) = f(x)], приходят к различным интегральным уравнениям относительно функции u(x):

Вообще, линейным интегральным уравнением 1-го рода называется уравнение вида

линейным интегральным уравнением 2-го рода, или уравнением Фредгольма,— уравнение вида

[при f (x) = 0 оно называется однородным уравнением Фредгольма]; обычно рассматриваются уравнения Фредгольма с параметром l:

Во всех уравнениях функция

— так называемое ядро интегрального уравнения — известна, так же, как функция f (x) (а £ х £ b); искомой является функция u(x) (а £ х £ b).

Функции K(x, y), f (x), u(x) и параметр уравнения l могут принимать как действительные, так и комплексные значения. В частном случае, когда ядро K(x, y) обращается в нуль при у > х, получается уравнение Вольтерра:

Интегральное уравнение называется особым, если хотя бы один из пределов интегрирования бесконечен или ядро K(x, y) обращается в бесконечность в одной или нескольких точках квадрата а £ х £ b, а £ y £ b или на некоторой линии. И. у. может относиться и к функциям нескольких переменных: таково, например, уравнение

Рассматриваются также нелинейные И. у., например уравнения вида

Линейные интегральные уравнение 2-го рода решаются следующими методами:

1) решение u(x) получается в виде ряда по степеням l (сходящегося в некотором круге |l|