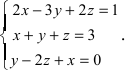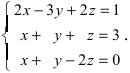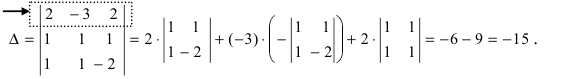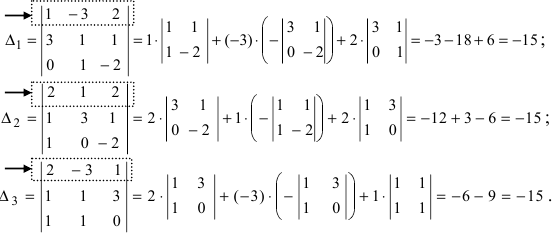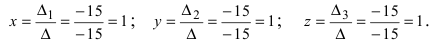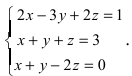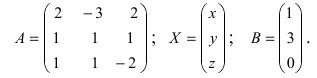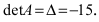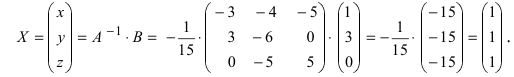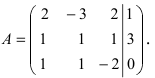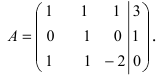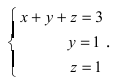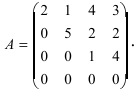Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 

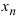
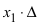
Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
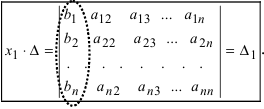
Определение: Определитель 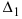
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 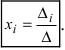
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 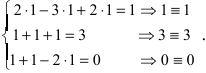
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 
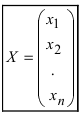
Тогда СЛАУ можно записать в матричном виде 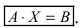
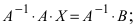
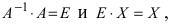
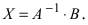
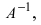
Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 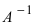
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 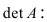
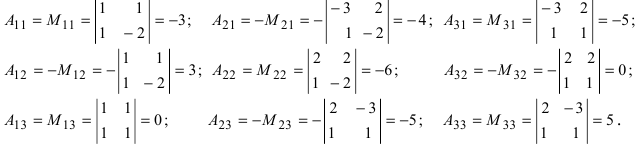
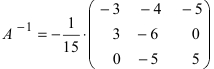
Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 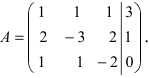
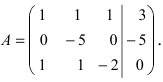
Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 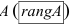
Если 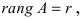
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 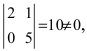
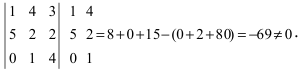
Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Примеры решения СЛАУ
Методы решения систем линейных уравнений широко используются в задачах математики, экономики, физики, химии и других науках. На практике, они позволяют не делать лишних действий, а записать систему уравнений в более компактной форме и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять основные методы решения и научиться выбирать оптимальный.
Перед изучением примеров решения задач советуем изучить теоретический материал по СЛАУ, прочитать все теоремы и методы решения. Список тем находится в правом меню.
Примеры по темам:
СЛАУ: основные понятия, виды
Задание. Проверить, является ли набор $<0,3>$ решением системы $\left\<\begin
Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$ :
$$3 x-2 y=-6 \Rightarrow 3 \cdot 0-2 \cdot 3=-6 \Rightarrow-6=-6$$ $$5 x+y=3 \Rightarrow 5 \cdot 0+3=3 \Rightarrow 3=3$$
Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.
Ответ. Набор $<0,3>$ является решением системы $\left\<\begin
Задание. Систему $\left\<\begin
Решение. Заданную СЛАУ записываем в матричной форме $A \cdot X=B$ , где матрица системы:
$$A=\left(\begin
$$A=\left(\begin
вектор-столбец свободных коэффициентов:
то есть, запись СЛАУ в матричной форме:
$$\left(\begin
Задание. Записать матрицу и расширенную матрицу системы $\left\<\begin
Решение. Матрица системы $A=\left(\begin
Критерий совместности системы
Задание. При каких значениях $\lambda$ система $\left\<\begin
Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываем расширенную матрицу системы $\tilde$ (слева от вертикальной черты находится матрица системы $A$ ):
и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от второй строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:
Третью строку складываем с первой:
и меняем первую и вторую строки матрицы местами
Квадратные СЛАУ. Матричный метод решения
Теоретический материал по теме — матричный метод решения.
Задание. Найти решение СЛАУ $\left\<\begin
Решение. Выпишем матрицу системы $\left\<\begin
$$X=\left(\begin
Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что $x_<1>=-11$, $x_<2>=31$
Ответ. $x_<1>=-11$, $x_<2>=31$
Задание. Решить с помощью обратной матрицы систему $\left\<\begin
Решение. Запишем данную систему в матричной форме:
где $A=\left(\begin
Найдем обратную матрицу $A^-1$ к матрице $A$ с помощью союзной матрицы:
Определитель матрицы $A$
$$\Delta=\left|\begin
Отсюда искомая матрица
Метод / Теорема Крамера
Теоретический материал по теме — метод Крамера.
Задание. Найти решение СЛАУ $\left\<\begin
Решение. Вычисляем определитель матрицы системы:
$$\Delta=\left|\begin
Так как $\Delta \neq 0$ , то по теореме Крамера система совместна и имеет единственное решение. вычислим вспомогательные определители. Определитель $\Delta_<1>$ получим из определителя $\Delta$ заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:
$$\Delta_<1>=\left|\begin
Аналогично, определитель $\Delta_<2>$ получается из определителя матрицы системы $\Delta$ заменой второго столбца столбцом свободных коэффициентов:
$$\Delta_<2>=\left|\begin
Тогда получаем, что
Ответ. $x_<-1>=-11$, $x_ <2>= 31$
Задание. При помощи формул Крамера найти решение системы $\left\<\begin
Решение. Вычисляем определитель матрицы системы:
$$\Delta=\left|\begin
Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:
$$\Delta_<1>=\left|\begin
Метод Гаусса. Метод последовательного исключения неизвестных
Теоретический материал по теме — метод Гаусса.
Задание. Решить СЛАУ $\left\<\begin
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_<1>$ равнялся 1 (это мы делаем для упрощения вычислений):
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac<1><2>$:
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
От третьей строки отнимаем вторую, умноженную на 3:
Умножив третью строку на $\left(-\frac<1><2>\right)$ , получаем:
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент $$\tilde \sim\left(\begin
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
Полученной матрице соответствует система
$\left\<\begin
Однородные СЛАУ. Фундаментальная система решений
Теоретический материал по теме — однородные СЛАУ.
Задание. Выяснить, имеет ли однородная СЛАУ $\left\<\begin
Решение. Вычислим определитель матрицы системы:
$$\Delta=\left|\begin
Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$
Ответ. Система имеет только нулевое решение.
Задание. Найти общее решение и ФСР однородной системы $\Delta=\left|\begin
Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):
$$A=\left(\begin
с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:
$$A \sim\left(\begin
Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:
$$A \sim\left(\begin
От четвертой строки отнимем $$\frac<4><3>$$ третьей и третью строку умножим на $$\frac<1><3>$$ :
$$A \sim\left(\begin
Нулевые строки можно далее не рассматривать, тогда получаем, что
$$A \sim\left(\begin
Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:
$$A \sim\left(\begin
то есть получаем систему, соответствующую данной матрице:
Или, выразив одни переменные через другие, будем иметь:
Здесь $x_<2>, x_<4>$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_<1>,x_<3>,x_<5>$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$
Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3-2$ (для проверки, это число должно равняться количеству свободных переменных).
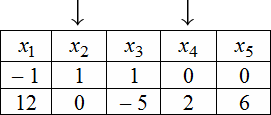
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
Тогда придавая в первом случае, например, независимым переменным значения $x_<2>=1$ , $x_<4>=0$ получаем, что $\left\<\begin
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:
Общее решение является линейной комбинацией частных решений:
$$X=C_ <1>X_<1>+C_ <2>X_<2>=C_<1>\left(\begin
где коэффициенты $C_<1>, C_<2>$ не равны нулю одновременно. Или запишем общее решение в таком виде:
Придавая константам $C_<1>, C_<2>$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.
Численные методы решения СЛАУ
Постановка задачи
Прикладные задачи, характерные для проектирования современных объектов новой техники, часто сводятся к многомерным в общем случае нелинейным уравнениям, которые решаются методом линеаризации, т.е. сведением нелинейных уравнений к линейным. В общем случае система [math]n[/math] уравнений с [math]n[/math] неизвестными записывается в виде
где [math]f_1,f_2,\ldots,f_n[/math] — функции [math]n[/math] переменных, нелинейные или линейные ( [math]x_i[/math] в функции [math]f_i[/math] входят в первых или частично в нулевых степенях). Здесь рассматривается частный случай задачи (1.1) — линейная неоднородная задача для систем линейных алгебраических уравнений (СЛАУ), которая сокращенно записывается в виде
где [math]A=(a_
i,\,j[/math] — переменные, соответствующие номерам строк и столбцов (целые числа); [math]b=(b_1,\ldots,b_n)^T\in \mathbb
x=(x_1,\ldots,x_n)^T\in \mathbb
1. Из линейной алгебры известно, что решение задачи (1.2) существует и единственно, если детерминант матрицы [math]A[/math] отличен от нуля, т.е. [math]\det A \equiv |A|\ne0[/math] ( [math]A[/math] — невырожденная матрица, называемая также неособенной).
2. Поставленная задача часто именуется первой задачей линейной алгебры. Подчеркнем, что в ней входными (исходными) данными являются матрица [math]A[/math] и вектор [math]b[/math] , а выходными — вектор [math]x[/math] .
3. Задача (1.2) имеет следующие особенности:
а) задача линейная (все переменные [math]x_[/math] , входящие в систему, имеют степени не выше первой) и неоднородная [math](b\ne0)[/math] ;
б) количество уравнений равно количеству неизвестных (система замкнута);
в) количество уравнений для некоторых практических задач велико: k\cdot10^3
г) при больших [math]n[/math] использовать формулу [math]x=A^<-1>b[/math] не рекомендуется в силу трудностей нахождения обратной матрицы.
4. Важнейшим признаком любой математической задачи, который надо в первую очередь принимать во внимание при ее анализе и выборе метода решения, является ее линейность или нелинейность. Это связано с тем, что нелинейные задачи с вычислительной точки зрения являются наиболее трудными. Так, нелинейная задача (1.1) является достаточно сложной при числе уравнений [math]n[/math] , пропорциональном [math]10^2[/math] , а линейная задача — при [math]n[/math] , пропорциональном [math]10^6[/math] .
Число обусловленности
Характер задачи и точность получаемого решения в большой степени зависят от ее обусловленности, являющейся важнейшим математическим понятием, влияющим на выбор метода ее решения. Поясним это понятие на примере двумерной задачи: [math]\begin
На рис. 1.1,б применительно к трем наборам входных данных, заданных с некоторыми погрешностями и соответствующих различным системам линейных уравнений, иллюстрируется характер обусловленности системы. Если [math]\det A[/math] существенно отличен от нуля, то точка пересечения пунктирных прямых, смещенных относительно сплошных прямых из-за погрешностей задания [math]A[/math] и [math]b[/math] , сдвигается несильно. Это свидетельствует о хорошей обусловленности системы. При [math]\det A\approx0[/math] небольшие погрешности в коэффициентах могут привести к большим погрешностям в решении (плохо обусловленная задача), поскольку прямые близки к параллельным. При [math]\det A=0[/math] прямые параллельны или они совпадают, и тогда решение задачи не существует или оно не единственно.
Более строго обусловленность задачи характеризуется числом обусловленности [math]\nu(A)= \|A\|\cdot \|A^<-1>\|[/math] , где [math]\|A\|[/math] — норма матрицы [math]A[/math] , а [math]\|A^<-1>\|[/math] — норма обратной матрицы. Чем больше это число, тем хуже обусловленность системы (при [math]\nu(A)\approx 10^3\div 10^4[/math] система линейных алгебраических уравнений плохо обусловлена). В качестве нормы матрицы может быть принято число, являющееся максимальным из сумм (по модулю) элементов всех строк этой матрицы. Подчеркнем, что реализация хорошей или плохой обусловленности в корректной и некорректной задачах напрямую связана с вытекающей отсюда численной устойчивостью или неустойчивостью. При этом для решения некорректных задач обычно применяются специальные методы или математические преобразования этих задач к корректным.
В численном анализе используются два класса численных методов решения систем линейных алгебраических уравнений:
1. Прямые методы , позволяющие найти решение за определенное число операций. К прямым методам относятся: метод Гаусса и его модификации (в том числе метод прогонки), метод [math]LU[/math] — разложения и др.
2. Итерационные методы , основанные на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений. Операции, входящие в повторяющийся процесс, составляют итерацию. К итерационным методам относятся: метод простых итераций, метод Зейделя и др.
Численные схемы реализации метода Гаусса
Рассмотрим частный случай решения СЛАУ — задачу нахождения решения системы линейных алгебраических уравнений
b=\begin
Согласно изложенному ранее, метод Гаусса содержит две совокупности операций, которые условно названы прямым ходом и обратным ходом.
Прямой ход состоит в исключении элементов, расположенных ниже элементов, соответствующих главной диагонали матрицы [math]A[/math] . При этом матрица [math]A[/math] с помощью элементарных преобразований преобразуется к верхней треугольной, а расширенная матрица [math](A\mid b)[/math] — к трапециевидной:
Заметим, что в отличие от общего подхода здесь не требуется приводить расширенную матрицу к упрощенному виду. Считается, что для реализации эффективных численных процедур достаточно свести проблему к решению системы с треугольной матрицей коэффициентов.
Обратный ход состоит в решении системы [math]\widetildex= \widetilde[/math] .
Алгоритм численного метода Гаусса
а) Положить номер шага [math]k=1[/math] . Переобозначить все элементы расширенной матрицы [math](A\mid b)[/math] через [math]a_
б) Выбрать ведущий элемент одним из двух способов.
Первый способ (схема единственного деления). Выбрать в качестве ведущего элемента [math]a_
Второй способ (схема с выбором ведущего элемента). На k-м шаге сначала переставить [math](n-k+1)[/math] оставшихся уравнений так, чтобы наибольший по модулю коэффициент при переменной [math]x_k[/math] попал на главную диагональ, а затем выбрать в качестве ведущего элемента [math]a_
в) каждый элемент строки, в которой находится ведущий элемент, поделить на него:
г) элементы строк, находящихся ниже строки с ведущим элементом, подсчитать по правилу прямоугольника, схематически показанного на рис. 10.1 (исключить элементы, стоящие ниже ведущего элемента).
Поясним алгоритм исключения на рис. 10.1. Пусть рассчитывается значение [math]a_
д) если [math]k\ne n[/math] , то перейти к пункту «б», где вместо [math]k[/math] положить [math]k+1[/math] .
Если [math]k=n[/math] , завершить прямой ход. Получена расширенная трапециевидная матрица из элементов [math]a_
1. Схема единственного деления имеет ограничение, связанное с тем, что ведущие элементы должны быть отличны от нуля. Одновременно желательно, чтобы они не были малыми по модулю, поскольку тогда погрешности при соответствующем делении будут большими. С этой точки зрения схема с выбором ведущего элемента является более предпочтительной.
2. По окончании прямого хода может быть вычислен определитель матрицы [math]A[/math] путем перемножения ведущих элементов.
3. В расчетных формулах все элементы расширенной матрицы обозначаются одним символом [math]a[/math] , так как они преобразуются по единым правилам.
4. Понятие нормы квадратной невырожденной матрицы позволяет исследовать влияние малых изменений правой части и элементов матрицы на решение систем линейных уравнений. Положительное число [math]A=\|A\|\cdot\|A^<-1>\|[/math] называется числом обусловленности матрицы . Существует и более общее определение числа обусловленности, применимое к вырожденным матрицам: [math]\operatorname
Пример 10.3. Найти число обусловленности матрицы системы [math]\begin
По формуле (4.2) для матрицы [math]A=\begin
В результате [math]\operatorname
При [math]b_1=11[/math] система имеет единственное решение [math]x_1=1,
x_2=1[/math] , а при [math]b_1=11,\!01[/math] , единственное решение [math]x_1=11,\!01,
x_2=0[/math] . Несмотря на малое различие в исходных данных: [math]\Delta b_1=|11-11,\!01|=0,\!01[/math] , полученные решения отличаются существенно: [math]\Delta x=\left\| \begin
Таким образом, решение плохо обусловленной системы может существенно изменяться даже при малых изменениях исходных данных.
Пример 10.4. Решить систему линейных алгебраических уравнений методом Гаусса (схема единственного деления)
1. Прямой ход. Запишем расширенную матрицу и реализуем прямой ход с помощью описанных преобразований:
Согласно пункту 2 замечаний 10.2 определитель матрицы системы равен произведению ведущих элементов: [math]\det=2\cdot\frac<1><2>\cdot26=26[/math] .
Решая эту систему, начиная с последнего уравнения, находим: [math]x_3=3,
Пример 10.5. Методом Гаусса с выбором ведущего элемента по столбцам решить систему:
1. Прямой ход. Реализуем поиск ведущего элемента по правилу: на k-м шаге переставляются [math](n-k+1)[/math] оставшихся уравнений так, чтобы наибольший по модулю коэффициент при [math]x_k[/math] попал на главную диагональ:
Согласно пункту 2 замечаний 10.2 определитель матрицы системы равен произведению ведущих элементов:
Решая ее, последовательно получаем: [math]x_3=1,
Пример 10.6. Решить систему уравнений методом Гаусса единственного деления
В результате получено решение: [math]x_<\ast>= \begin
Метод прогонки для решения СЛАУ
Метод применяется в случае, когда матрица [math]A[/math] — трехдиагональная. Сформулируем общую постановку задачи.
Дана система линейных алгебраических уравнений с трехдиагональной матрицей [math]A[/math] . Развернутая запись этой системы имеет вид
которому соответствует расширенная матрица
Здесь первое и последнее уравнения, содержащие по два слагаемых, знак минус (–) при коэффициенте [math]\beta_i[/math] взят для более удобного представления расчетных формул метода.
Если к (10.2) применить алгоритм прямого хода метода Гаусса, то вместо исходной расширенной матрицы получится трапециевидная:
Учитывая, что последний столбец в этой матрице соответствует правой части, и переходя к системе, включающей неизвестные, получаем рекуррентную формулу:
Соотношение (10.3) есть формула для обратного хода, а формулы для коэффициентов [math]P_i,\,Q_i[/math] которые называются прогоночными , определяются из (10.2), (10.3). Запишем (10.3) для индекса [math]i-1\colon[/math] [math]x_
Приводя эту формулу к виду (10.3) и сравнивая, получаем рекуррентные соотношения для [math]P_i,\,Q_i\colon[/math]
Определение прогоночных коэффициентов по формулам (10.4) соответствует прямому ходу метода прогонки.
Обратный ход метода прогонки начинается с вычисления [math]x_n[/math] . Для этого используется последнее уравнение, коэффициенты которого определены в прямом ходе, и последнее уравнение исходной системы:
Тогда определяется [math]x_n:[/math]
Остальные значения неизвестных находятся по рекуррентной формуле (10.3).
Алгоритм решения систем уравнений методом прогонки
Q_1=-\frac<\delta_1><\beta_1>[/math] (в (10.4) подставить [math]\alpha_1=0[/math] ).
2. Вычислить прогоночные коэффициенты: [math]P_2,Q_2;\,P_3,Q_3;\,\ldots;\,P_
2. Значения [math]x_
1. Аналогичный подход используется для решения систем линейных алгебраических уравнений с пятидиагональными матрицами.
2. Алгоритм метода прогонки называется корректным, если для всех [math]i=1,\ldots,n,
\beta_i-\alpha_iP_
3. Достаточным условием корректности и устойчивости прогонки является условие преобладания диагональных элементов в матрице [math]A[/math] , в которой [math]\alpha_i\ne0[/math] и [math]\gamma_i\ne0[/math] [math](i=2,3,\ldots,n-1)\colon[/math]
и в (10.6) имеет место строгое неравенство хотя бы при одном [math]i[/math] .
4. Алгоритм метода прогонки является экономичным и требует для своей реализации количество операций, пропорциональное [math]n[/math] .
Пример 10.7. Дана система линейных алгебраических уравнений с трехдиагональной матрицей [math]A
\gamma_4=0)[/math] . Решить эту систему методом прогонки.
Данная система удовлетворяет условию преобладания диагональных элементов (10.3): в первом уравнении 3″>[math]5>3[/math] , во втором уравнении 3+1″>[math]6>3+1[/math] ; в третьем уравнении 1+2″>[math]4>1+2[/math] , в четвертом уравнении 1″>[math]3>1[/math] . Далее выполняем прямой и обратный ход, учитывая, что расширенная матрица имеет вид
1. Прямой ход. Вычислим прогоночные коэффициенты:
Подчеркнем, что [math]\beta_1=-5;
\beta_4=3[/math] , так как в (10.2) во втором слагаемом взят знак «минус»:
Подстановкой решения [math]x_<\ast>=\begin
i=1,2,3,4;[/math] [math]|P_i| , т.е. метод прогонки оказался корректным и устойчивым (см. пункт 3 замечаний 10.3).
Для наглядности представления информации исходные данные и результаты расчетов поместим в табл. 10.1, где в первых четырех колонках содержатся исходные данные, а в последних трех — полученные результаты.
Пример 10.8. Дана система линейных алгебраических уравнений с трехдиагональной матрицей [math]A[/math] , решить систему методом прогонки:
Результаты расчетов в прямом и обратном ходе занесены в табл. 10.2.
В результате получено решение: [math]x_<\ast>=\begin
Пример 10.9. Решить методом прогонки систему уравнений
Расширенная матрица системы имеет вид [math]\begin
1. Прямой ход. Вычислим прогоночные коэффициенты:
Получено решение системы: [math]x_<\ast>=\begin
Метод LU-разложения для решения СЛАУ
Рассмотрим ещё один метод решения задачи (10.1). Метод опирается на возможность представления квадратной матрицы [math]A[/math] системы в виде произведения двух треугольных матриц:
где [math]L[/math] — нижняя, a [math]U[/math] — верхняя треугольные матрицы,
С учётом (10.7) система [math]Ax=b[/math] представляется в форме
Решение системы (10.8) сводится к последовательному решению двух простых систем с треугольными матрицами. В итоге процедура решения состоит из двух этапов.
Прямой ход. Произведение [math]Ux[/math] обозначим через [math]y[/math] . В результате решения системы [math]Ly=b[/math] находится вектор [math]y[/math] .
Обратный ход. В результате решения системы [math]Ux=y[/math] находится решение задачи — столбец [math]x[/math] .
В силу треугольности матриц [math]L[/math] и [math]U[/math] решения обеих систем находятся рекуррентно (как в обратном ходе метода Гаусса).
Из общего вида элемента произведения [math]A=LU[/math] , а также структуры матриц [math]L[/math] и [math]U[/math] следуют формулы для определения элементов этих матриц:
Результат представления матрицы [math]A[/math] в виде произведения двух треугольных матриц (операции факторизации) удобно хранить в одной матрице следующей структуры:
Вычисления на k-м шаге метода LU-разложения удобно производить, пользуясь двумя схемами, изображенными на рис. 10.2.
1. Всякую квадратную матрицу [math]A[/math] , имеющую отличные от нуля угловые миноры
можно представить в виде LU-разложения, причем это разложение будет единственным. Это условие выполняется для матриц с преобладанием диагональных элементов, у которых
2. В результате прямого хода может быть вычислен определитель матрицы [math]A[/math] по свойствам определителя произведения матриц (теорема 2.2) и определителя треугольных матриц:
Алгоритм метода LU-разложение
1. Выполнить операцию факторизации исходной матрицы [math]A[/math] , применяя схемы (рис. 10.2) или формулы (10.9), и получить матрицы [math]L[/math] и [math]U[/math] .
2. Решить систему [math]L\cdot y=b[/math] .
3. Решить систему [math]U\cdot x=b[/math] .
Пример 10.10. Решить систему линейных алгебраических уравнений методом LU-разложения
1. Выполним операцию факторизации:
В результате получены две треугольные матрицы:
Согласно пункту 2 замечаний 10.4, определитель матрицы [math]A[/math] находится в результате перемножения диагональных элементов матрицы [math]L\colon\,\det=2\cdot0,\!5\cdot26=26[/math] .
2. Решим систему [math]L\cdot y=b[/math] :
\begin
3. Решим систему [math]U\cdot x=y:[/math]
\begin
Пример 10.11. Решить систему линейных алгебраических уравнений методом LU-разложения.
1. Выполним операцию факторизации:
2. Решим систему линейных уравнений [math]L\cdot y=b[/math] :
\begin
3. Решим систему [math]U\cdot x=y[/math] :
\begin
Пример 10.12. Решить систему линейных алгебраических уравнений методом LU-разложения
1. Выполним процедуру факторизации:
В результате получаем матрицы LU-разложения:
2. Решим систему уравнений [math]L\cdot y=b:[/math]
\begin
3. Решим систему уравнений [math]U\cdot x=y:[/math]
Отсюда записываем решение исходной системы уравнений: [math]x_<\ast>= \begin
Метод квадратных корней для решения СЛАУ
При решении систем линейных алгебраических уравнений с симметрическими матрицами можно сократить объем вычислений почти вдвое.
Пусть [math]A[/math] — симметрическая квадратная матрица системы [math]Ax=b[/math] порядка [math]n[/math] . Решим задачу ее представления в виде
Находя произведение [math]U^T\cdot U[/math] , составим систему уравнении относительно неизвестных элементов матрицы [math]U:[/math]
Система имеет следующий вид:
Из первой строки системы находим
Из второй строки определяем
Из последней строки имеем [math]\textstyle
Таким образом, элементы матрицы [math]U[/math] находятся из соотношений
При осуществлении [math]U^TU[/math] -разложения симметрической матрицы могут возникать ситуации, когда [math]u_
Если матрица [math]A[/math] представима в форме [math]U^TU[/math] , то система [math]Ax=b[/math] имеет вид [math]U^TUx=b[/math] . Решение этой системы сводится к последовательному решению двух систем с треугольными матрицами. В итоге процедура решения состоит их двух этапов.
1. Прямой ход. Произведение [math]Ux[/math] обозначается через [math]y[/math] . В результате решения системы [math]U^Ty=b[/math] находится столбец [math]y[/math] .
2. Обратный ход. В результате решения системы [math]Ux=y[/math] находится решение задачи — столбец [math]x[/math] .
Алгоритм метода квадратных корней
1. Представить матрицу [math]A[/math] в форме [math]A=U^T\cdot U[/math] , используя (10.10).
2. Составить систему уравнений [math]U^T\cdot y=b[/math] и найти [math]y[/math] .
3. Составить систему уравнений [math]U\cdot x=y[/math] и найти [math]x[/math] .
Найти решение системы уравнений методом квадратных корней
Решение. 1. Представим матрицу [math]A[/math] в форме [math]A=U^T\cdot U[/math] , используя (10.10):
при [math]i=1[/math] получаем [math]u_<11>= \sqrt
при [math]i=2[/math] имеем
Таким образом, получили
2. Решим систему [math]U^T\cdot y=b[/math] :
3. Решим систему [math]U\cdot x=y[/math] :
В результате получили решение исходной системы [math]x_1=1,
Метод простых итераций для решения СЛАУ
Альтернативой прямым методам решения СЛАУ являются итерационные методы, основанные на многократном уточнении [math]x^<(0)>[/math] , заданного приближенного решения системы [math]A\cdot x=b[/math] . Верхним индексом в скобках здесь и далее по тексту обозначается номер итерации (совокупности повторяющихся действий).
Реализация простейшего итерационного метода — метода простых итераций — состоит в выполнении следующих процедур.
1. Исходная задача [math]A\cdot x=b[/math] преобразуется к равносильному виду:
где [math]\alpha[/math] — квадратная матрица порядка [math]n[/math] ; [math]\beta[/math] — столбец. Это преобразование может быть выполнено различными путями, но для обеспечения сходимости итераций (см. процедуру 2) нужно добиться выполнения условия [math]\|\alpha\| .
2. Столбец [math]\beta[/math] принимается в качестве начального приближения [math]x^<(0)>= \beta[/math] и далее многократно выполняются действия по уточнению решения, согласно рекуррентному соотношению
или в развернутом виде
3. Итерации прерываются при выполнении условия (где 0″>[math]\varepsilon>0[/math] — заданная точность, которую необходимо достигнуть при решении задачи)
1. Процесс (10.12) называется параллельным итерированием , так как для вычисления (k+1)-го приближения всех неизвестных учитываются вычисленные ранее их k-е приближения.
2. Начальное приближение [math]x^<(0)>[/math] может выбираться произвольно или из некоторых соображений. При этом может использоваться априорная информация о решении или просто «грубая» прикидка. При выполнении итераций (любых) возникают следующие вопросы:
а) сходится ли процесс (10.12), т.е. имеет ли место [math]x^<(k)>\to x_<\ast>[/math] , при [math]k\to\infty[/math] , где [math]x_<\ast>[/math] — точное решение?
б) если сходимость есть, то какова ее скорость?
в) какова погрешность найденного решения [math]x^<(k+1)>[/math] , т.е. чему равна норма разности [math]\bigl\|x^<(k)>-x_<\ast>\bigr\|[/math] ?
Ответ на вопросы о сходимости дают следующие две теоремы.
Теорема (10.1) о достаточном условии сходимости метода простых итераций. Метод простых итераций, реализующийся в процессе последовательных приближений (10.12), сходится к единственному решению исходной системы [math]Ax=b[/math] при любом начальном приближении [math]x^<(0)>[/math] со скоростью не медленнее геометрической прогрессии, если какая-либо норма матрицы [math]\alpha[/math] меньше единицы, т.е. [math]\|\alpha\|_s .
1. Условие теоремы 10.1, как достаточное, предъявляет завышенные требования к матрице [math]\alpha[/math] , и потому иногда сходимость будет, если даже [math]\|\alpha\|\geqslant1[/math] .
2. Сходящийся процесс обладает свойством «самоисправляемости», т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, так как ошибочное приближение можно рассматривать, как новое начальное.
3. Условия сходимости выполняются, если в матрице [math]A[/math] диагональные элементы преобладают, т.е.
и хотя бы для одного [math]i[/math] неравенство строгое. Другими словами, модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов (свободные члены не рассматриваются).
4. Чем меньше величина нормы [math]\|\alpha\|[/math] , тем быстрее сходимость метода.
Теорема (10.2) о необходимом и достаточном условии сходимости метода простых итераций. Для сходимости метода простых итераций (10.12) при любых [math]x^<(0)>[/math] и [math]\beta[/math] необходимо и достаточно, чтобы собственные значения матрицы [math]\alpha[/math] были по модулю меньше единицы, т.е. [math]\bigl|\lambda_i(\alpha)\bigr| .
Замечание 10.7. Хотя теорема 10.2 дает более общие условия сходимости метода простых итераций, чем теорема 10.1, однако ею воспользоваться сложнее, так как нужно предварительно вычислить границы собственных значений матрицы [math]\alpha[/math] или сами собственные значения.
Преобразование системы [math]Ax=b[/math] к виду [math]x=\alpha x+\beta[/math] с матрицей [math]\alpha[/math] , удовлетворяющей условиям сходимости, может быть выполнено несколькими способами. Приведем способы, используемые наиболее часто.
1. Уравнения, входящие в систему [math]Ax=b[/math] , переставляются так, чтобы выполнялось условие (10.14) преобладания диагональных элементов (для той же цели можно использовать другие элементарные преобразования). Затем первое уравнение разрешается относительно [math]x_1[/math] , второе — относительно [math]x_2[/math] и т.д. При этом получается матрица [math]\alpha[/math] с нулевыми диагональными элементами.
Например, система [math]\begin
|4|>|-2,\!8|+|1|[/math] , т.е. диагональные элементы преобладают.
Выражая [math]x_1[/math] из первого уравнения, [math]x_2[/math] — из второго, а [math]x_3[/math] — из третьего, получаем систему вида [math]x=\alpha x+\beta:[/math]
Заметим, что [math]\|\alpha\|_1=\max\<0,\!9;\,0,\!8;\,0,\!95 \>=0,\!95 , т.е. условие теоремы 10.1 выполнено.
Проиллюстрируем применение других элементарных преобразований. Так, система [math]\begin
2. Уравнения преобразуются так, чтобы выполнялось условие преобладания диагональных элементов, но при этом коэффициенты [math]\alpha_
Например, систему [math]\begin
i,j=1,\ldots,n[/math] достаточно малы, условие сходимости выполняется.
Алгоритм метода простых итераций
1. Преобразовать систему [math]Ax=b[/math] к виду [math]x=\alpha x+\beta[/math] одним из описанных способов.
2. Задать начальное приближение решения [math]x^<(0)>[/math] произвольно или положить [math]x^<(0)>=\beta[/math] , а также малое положительное число [math]\varepsilon[/math] (точность). Положить [math]k=0[/math] .
3. Вычислить следующее приближение [math]x^<(k+1)>[/math] по формуле [math]x^<(k+1)>= \alpha x^<(k)>+\beta[/math] .
4. Если выполнено условие [math]\bigl\|x^<(k+1)>-x^<(k)>\bigr\| , процесс завершить и в качестве приближенного решения задачи принять [math]x_<\ast>\cong x^<(k+1)>[/math] . Иначе положить [math]k=k+1[/math] и перейти к пункту 3 алгоритма.
Методом простых итераций с точностью [math]\varepsilon=0,\!01[/math] решить систему линейных алгебраических уравнений:
Решение. 1. Так как [math]|2| , то условие (5.41) не выполняется. Переставим уравнения так, чтобы выполнялось условие преобладания диагональных элементов:
|10|>|2|+|2|[/math] . Выразим из первого уравнения [math]x_1[/math] , из второго [math]x_2[/math] , из третьего [math]x_3:[/math]
Заметим, что [math]\|\alpha\|_1= \ma\<0,\!2;\,0,\!3;\,0,\!4 \>=0,\!4 , следовательно, условие сходимости (теорема 10.1) выполнено.
2. Зададим [math]x^<(0>=\beta= \begin
3. Выполним расчеты по формуле (10.12):
до выполнения условия окончания и результаты занесем в табл. 10.4.
4. Расчет закончен, поскольку выполнено условие окончания [math]\bigl\|x^<(k+1)>-x^ <(k)>\bigr\|=0,\!0027 .
Приближенное решение задачи: [math]x_<\ast>\cong \begin
Приведем результаты расчетов для другого начального приближения [math]x^<(0)>=\begin
Приближенное решение задачи: [math]x_<\ast>\cong \begin
Метод Зейделя для решения СЛАУ
Этот метод является модификацией метода простых итераций и в некоторых случаях приводит к более быстрой сходимости.
Итерации по методу Зейделя отличаются от простых итераций (10.12) тем, что при нахождении i-й компоненты (k+1)-го приближения сразу используются уже найденные компоненты (к +1) -го приближения с меньшими номерами [math]1,2,\ldots,i-1[/math] . При рассмотрении развернутой формы системы итерационный процесс записывается в виде
В каждое последующее уравнение подставляются значения неизвестных, полученных из предыдущих уравнений.
Теорема (10.3) о достаточном условии сходимости метода Зейделя. Если для системы [math]x=\alpha x+\beta[/math] какая-либо норма матрицы [math]\alpha[/math] меньше единицы, т.е. [math]\|\alpha\|_s , то процесс последовательных приближений (10.15) сходится к единственному решению исходной системы [math]Ax=b[/math] при любом начальном приближении [math]x^<(0)>[/math] .
Записывая (10.15) в матричной форме, получаем
где [math]L,\,U[/math] являются разложениями матрицы [math]\alpha:[/math]
Преобразуя (10.16) к виду [math]x=\alpha x+\beta[/math] , получаем матричную форму итерационного процесса метода Зейделя:
Тогда достаточное, а также необходимое и достаточное условия сходимости будут соответственно такими (см. теоремы 10.1 и 10.2):
1. Для обеспечения сходимости метода Зейделя требуется преобразовать систему [math]Ax=b[/math] к виду [math]x=\alpha x+\beta[/math] с преобладанием диагональных элементов в матрице а (см. метод простых итераций).
2. Процесс (10.15) называется последовательным итерированием , так как на каждой итерации полученные из предыдущих уравнений значения подставляются в последующие. Как правило, метод Зейделя обеспечивает лучшую сходимость, чем метод простых итераций (за счет накопления информации, полученной при решении предыдущих уравнений). Метод Зейделя может сходиться, если расходится метод простых итераций, и наоборот.
3. При расчетах на ЭВМ удобнее пользоваться формулой (10.16).
4. Преимуществом метода Зейделя, как и метода простых итераций, является его «самоисправляемость».
5. Метод Зейделя имеет преимущества перед методом простых итераций, так как он всегда сходится для нормальных систем линейных алгебраических уравнений, т.е. таких систем, в которых матрица [math]A[/math] является симметрической и положительно определенной. Систему линейных алгебраических уравнений с невырожденной матрицей [math]A[/math] всегда можно преобразовать к нормальной, если ее умножить слева на матрицу [math]A^T[/math] (матрица [math]A^TA[/math] — симметрическая). Система [math]A^TAx= A^Tb[/math] является нормальной.
Алгоритм метода Зейделя
1. Преобразовать систему [math]Ax=b[/math] к виду [math]x=\alpha x+\beta[/math] одним из описанных способов.
2. Задать начальное приближение решения [math]x^<(0)>[/math] произвольно или положить [math]x^<(0)>=\beta[/math] , а также малое положительное число [math]\varepsilon[/math] (точность). Положить [math]k=0[/math] .
3. Произвести расчеты по формуле (10.15) или (10.16) и найти [math]x^<(k+1)>[/math] .
4. Если выполнено условие окончания [math]\bigl\|x^<(k+1)>-x^<(k)>\bigr\| , процесс завершить и в качестве приближенного решения задачи принять [math]x_<\ast>\cong x^<(k+1)>[/math] . Иначе положить [math]k=k+1[/math] и перейти к пункту 3.
Пример 10.15. Методом Зейделя с точностью [math]\varepsilon=0,\!001[/math] решить систему линейных алгебраических уравнений:
1. Приведем систему [math]Ax=b[/math] к виду [math]x=\alpha x+\beta[/math] (см. пример 10.14):
Так как [math]\|\alpha\|_1=\max\<0,\!2;\,0,\!3;\,0,\!4 \>=0,\!4 , условие сходимости выполняется.
2. Зададим [math]x^<(0)>= \begin
Выполним расчеты по формуле (10.15): [math]\begin
Очевидно, найденное решение [math]x_<\ast>= \begin
4. Расчет завершен, поскольку выполнено условие окончания [math]\bigl\|x^<(k+1)>-x^<(k)>\bigr\|= 0,\!0004 .
Пример 10.16. Методом Зейделя с точностью [math]\varepsilon=0,\!005[/math] решить систему линейных алгебраических уравнений:
|5|>|-1|+|-2|[/math] , в данной системе диагональные элементы преобладают. Выразим из первого уравнения [math]x_1[/math] , из второго [math]x_2[/math] , из третьего [math]x_3:[/math]
2. Зададим [math]x^<(0)>= \begin
k=0,1,\ldots[/math] и результаты занесем в табл. 10.7.
Очевидно, найденное решение [math]x_<\ast>= \begin
4. Расчет завершен, поскольку выполнено условие окончания [math]\bigl\|x^<(k+1)>-x^<(k)>\bigr\|= 0,\!001 .
http://www.webmath.ru/poleznoe/formules_5_7.php
http://mathhelpplanet.com/static.php?p=chislennyye-metody-resheniya-slau
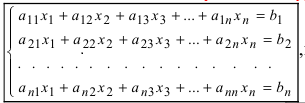

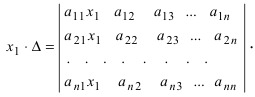
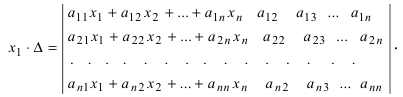

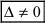 ), то система имеет единственное решение;
), то система имеет единственное решение;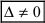 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 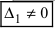 или
или 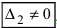 , или, . или
, или, . или 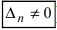 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);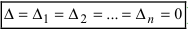 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.