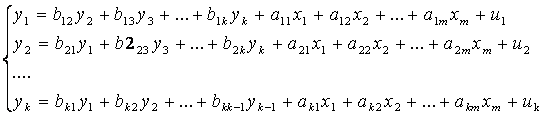Методы решения систем одновременных уравнений

Система одновременных эконометрических уравнений

Вы будете перенаправлены на Автор24

Общие сведения о системе одновременных эконометрических уравнений

Система одновременных экономических уравнений – это совокупность уравнений, которые позволяют исследователям установить наличие и степень связи (взаимозависимости) между эконометрическими переменными.

Выделяют две группы экономических переменных, из которых образуют эконометрические уравнения:

• эндогенные переменные, чьи значения определяют в результате функционирования изучаемой экономической системы (эндогенные переменные зависят как от экзогенных, так и от других эндогенных переменных);
• экзогенные переменные, чьи значения задаются извне (т.е. определяются вне эконометрической модели) и являются основой для определения значений эндогенных переменных (экзогенные переменные являются независимыми).

Функционирование сложных экономических систем может быть объяснено благодаря построению изолированных уравнений регрессии и измерению на их основе тесноты связи между переменными. Однако истинное влияние отдельных признаков на вариацию результирующей переменной не может быть описано одним отдельно взятым уравнением регрессии. В связи с этим в изучении экономических процессов важное значение приобрело структурирование связей между системой переменных.

В качестве примера системы одновременных эконометрических уравнений можно привести простейшую макроэкономическую (кейнсианскую) модель, которая состоит из двух уравнений:

В данной модели эндогенными переменными являются C (расходы на потребление) и Y (доход), а экзогенной переменной – I (инвестиции). b представляет собой коэффициент, который выражает предельную склонность к потреблению.

Характеристика структурной и приведенной форм системы уравнений

Данная система от всех других систем уравнения отличается наличием определенной структурной формы эконометрической модели. Это форма предполагает, что в правых и левых частях разных уравнений системы находятся одни и те же экономические переменные. Структурная форма системы одновременных эконометрических уравнений в случае переноса всех эндогенных переменных в левую часть может быть представлено в следующем матричном виде: YA = XB + E.

Готовые работы на аналогичную тему

Кроме структурной также выделяют приведенную (прогнозную) форму системы. По сути она есть представление системы, в котором эндогенные переменные выражены через экзогенные, то есть в каждом уравнении имеется только одна эндогенная переменная. Тогда она выглядит так: Y = XП + U.

Приведенную форму системы всегда можно получить, если задана структурная форма. Однако обратное действие не всегда возможно, а если оно и возможно, то не всегда получается однозначный результат.

Если через коэффициенты приведенной формы можно выразить коэффициенты структурного уравнения, то оно называется идентифицируемым (в противном случае оно – неидентифицируемое). Точная индентифицируемость свойственна ситуации, когда способ подобного выражения является единственным. Если же их несколько, то говорят о сверхидентифицируемости.

Чтобы имела место идентифицируемость, требуется выполнение такого необходимого условия, как непревышение количества переменных правой части уравнения над количеством всех экзогенных переменных системы. Формулировка этого условия может отличаться. Так, часто говорят: количество экзогенных переменных, которые исключены из данного уравнения, должно быть не меньше количества эндогенных переменных, которые включены в уравнение, за вычетом единицы.

Также выделяют условие, достаточное для признания идентифицируемости системы. Оно заключается в том, чтобы общее число эндогенных переменных системы за вычетом единицы не превышало ранг матрицы, который составлен из коэффициентов (в других уравнениях) при переменных, отсутствующих в данном уравнении.

Методы оценки систем одновременных эконометрических уравнений

Для того, чтобы оценить представленные в структурной форме уравнения системы, нецелесообразно непосредственно применять обычный метод наименьших квадратов. Это связано с тем, что подобное применение нарушит важнейшее условие регрессионного анализа — экзогенность (предопределенность, независимость) факторов. Тогда будут получены смещённые и несостоятельные оценки параметров.

Поэтому системы одновременных эконометрических уравнений оценивают посредством применения следующих методов:

• косвенный метод наименьших квадратов – подстановка в аналитическое выражение зависимости структурных коэффициентов от их приведённых оценок, которые получают в результате применения обычного метода наименьших квадратов;
• двухшаговый метод наименьших квадратов – оценивание сначала зависимости эндогенных переменных от всех экзогенных (первый шаг), а затем – структурной формы модели, в которой эндогенные переменные заменены на их оценки, полученные на первом шаге (второй шаг);
• трехшаговый метод наименьших квадратов – предыдущий метод дополняется третьим шагом, с помощью которого оценивают ковариационную матрицу вектора случайных ошибок системы уравнений;
• методы максимального правдоподобия – использование всей информации об ограничениях на приведённую форму эконометрической модели.

Системы эконометрических уравнений

Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а₀ + а₁х + а₂р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.

Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
   
2. Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:

От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:

Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.

Проблема идентификации

Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.

Правила идентификации

Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y₃, x₂, х₃:
y₃ x ₂ x₃
b₁₃ a ₁₃ 0 — в 1-ом уравнении
1 a₃₂ a₃₃ — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y₁, x₂:
y ₁ x ₂
1 a₁₂ — в 1-ом уравнении
b₂₁ 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.

Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.

Каковы уравнения одновременности? (с решенными упражнениями)

одновременные уравнения это те уравнения, которые должны выполняться одновременно. Следовательно, чтобы иметь одновременные уравнения, нужно иметь более одного уравнения.

Когда у вас есть два или более разных уравнения, которые должны иметь одно и то же решение (или одинаковые решения), вы говорите, что у вас есть система уравнений, или вы говорите, что у вас есть одновременные уравнения.

Когда у вас есть одновременные уравнения, может случиться так, что они не имеют общих решений или имеют конечное количество или имеют бесконечное количество.

Одновременные уравнения

Учитывая два разных уравнения Eq1 и Eq2, мы имеем, что система этих двух уравнений называется уравнениями одновременности.

Уравнения одновременного выполнения показывают, что если S является решением уравнения (1), то S также является решением уравнения (2) и наоборот

черты

Когда речь идет о системе одновременных уравнений, вы можете иметь 2 уравнения, 3 уравнения или N уравнений.

Наиболее распространенные методы, которые используются для решения одновременных уравнений: подстановка, выравнивание и редукция. Существует также другой метод, называемый правилом Крамера, который очень полезен для систем с более чем двумя уравнениями одновременно..

Примером одновременных уравнений является система

Уравнение 2: 2x-y = 1

Можно заметить, что x = 0, y = 2 является решением уравнения Eq1, но не является решением уравнения Eq2.

Единственное общее решение, которое имеют оба уравнения, это x = 1, y = 1. То есть x = 1, y = 1 — решение системы уравнений.

Решенные упражнения

Затем мы приступим к решению системы уравнений, показанной выше, с помощью 3 упомянутых методов.

Первое упражнение

Решите систему уравнений Eq1: x + y = 2, Eq2 = 2x-y = 1, используя метод подстановки.

решение

Метод подстановки состоит в очистке одного из неизвестных одного из уравнений, а затем замене его в другом уравнении. В этом конкретном случае вы можете очистить «y» из уравнения Eq1 и получить y = 2-x.

При замене этого значения «y» в уравнении 2 получается, что 2x- (2-x) = 1. Таким образом, мы получаем, что 3x-2 = 1, то есть x = 1.

Затем, поскольку значение x известно, оно подставляется в «y» и получается y = 2-1 = 1..

Поэтому единственное решение системы одновременных уравнений Eq1 и Eq2 — это x = 1, y = 1.

Второе упражнение

Решить систему уравнений Eq1: x + y = 2, Eq2 = 2x-y = 1, используя метод выравнивания.

решение

Метод выравнивания состоит в том, чтобы очистить один и тот же вопрос от обоих уравнений, а затем выровнять полученные уравнения..

Очистив «x» от обоих уравнений, мы получим, что x = 2-y, а x = (1 + y) / 2. Теперь эти два уравнения приравнены, и мы получаем, что 2-y = (1 + y) / 2, где получается, что 4-2y = 1 + y.

Группировка неизвестного «у» на одной стороне приводит к у = 1. Теперь, когда вы знаете «и», вы приступаете к поиску значения «x». При замене y = 1 получаем, что x = 2-1 = 1.

Следовательно, общее решение между уравнениями Eq1 и Eq2 имеет вид x = 1, y = 1.

Третье упражнение

Решите систему уравнений Eq1: x + y = 2, Eq2 = 2x-y = 1, используя метод редукции.

решение

Метод редукции состоит в умножении уравнений, заданных на соответствующие коэффициенты, так что при сложении этих уравнений одна из переменных отменяется.

В этом конкретном примере вам не нужно умножать какое-либо уравнение на какой-либо коэффициент, просто сложите их вместе. При сложении Eq1 плюс Eq2 получаем, что 3x = 3, из чего получаем, что x = 1.

Оценивая x = 1 в уравнении (1), получаем, что 1 + y = 2, из чего получается, что y = 1.

Следовательно, x = 1, y = 1 — единственное решение уравнений уравнения Eq1 и Eq2..

Четвертое упражнение

Решить систему уравнений одновременного уравнения (2x-3y = 8) и уравнения (2): 4x-3y = 12.

решение

Это упражнение не требует какого-либо конкретного метода, поэтому вы можете применить метод, который наиболее удобен для каждого читателя.

В этом случае будет использован метод сокращения. Умножение Eq1 на -2 дает уравнение Eq3: -4x + 6y = -16. Теперь, добавив Eq3 и Eq2, получим 3y = -4, поэтому y = -4 / 3.

Теперь при оценке y = -4 / 3 в уравнении (1) мы получаем, что 2x-3 (-4/3) = 8, где 2x + 4 = 8, следовательно, x = 2.

В заключение, единственное решение системы одновременных уравнений Eq1 и Eq2 — это x = 2, y = -4 / 3..

наблюдение

Методы, описанные в этой статье, могут быть применены к системам с более чем двумя уравнениями одновременно.

Чем больше уравнений и больше неизвестных, тем сложнее процедура решения системы..

Любой метод решения систем уравнений даст одинаковые решения, то есть решения не зависят от применяемого метода..