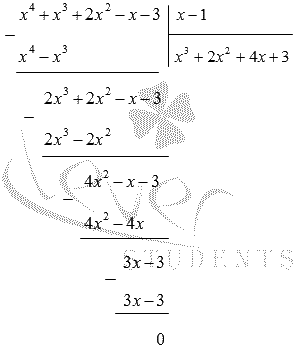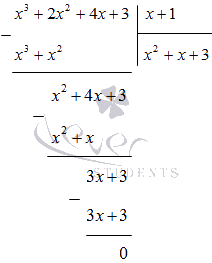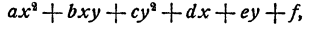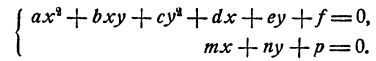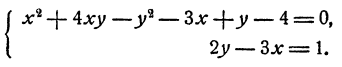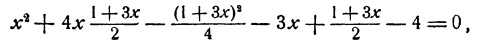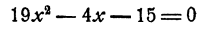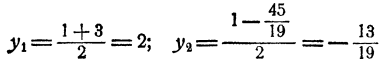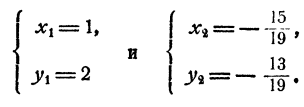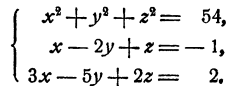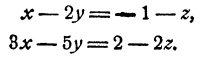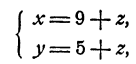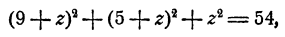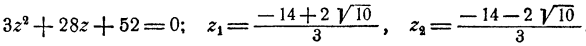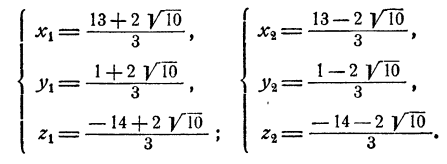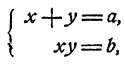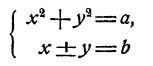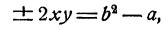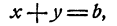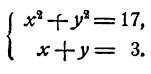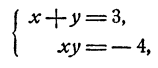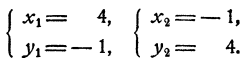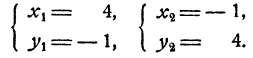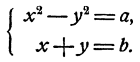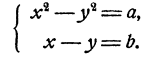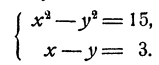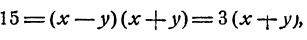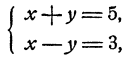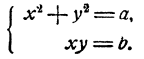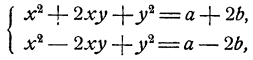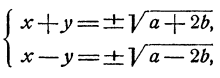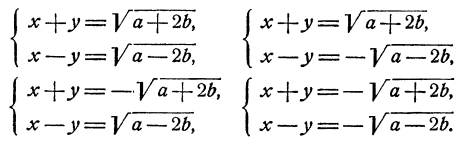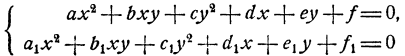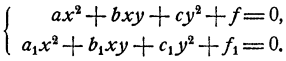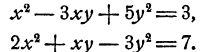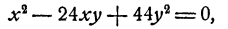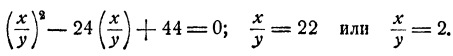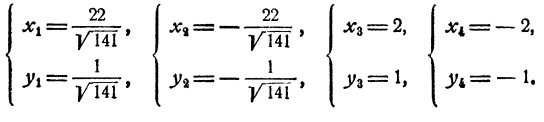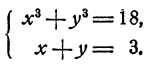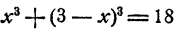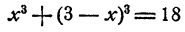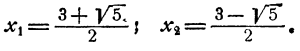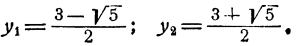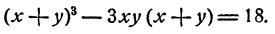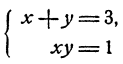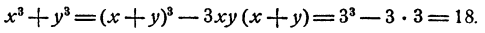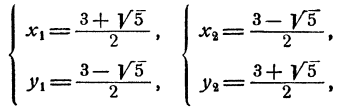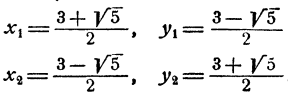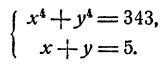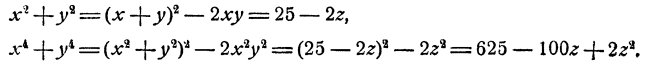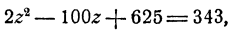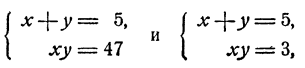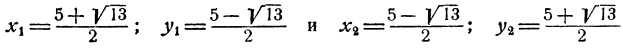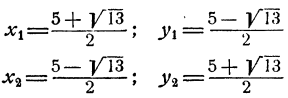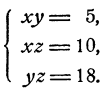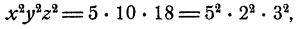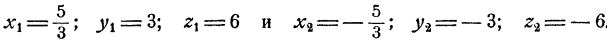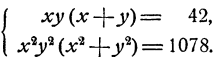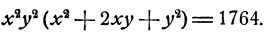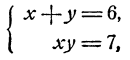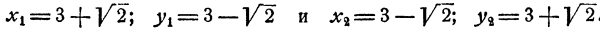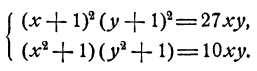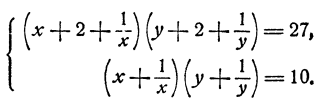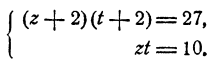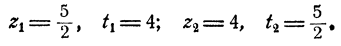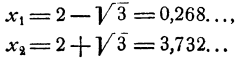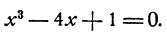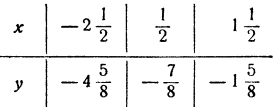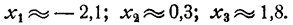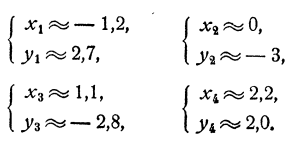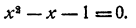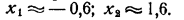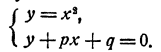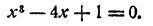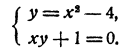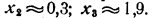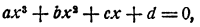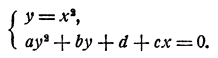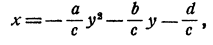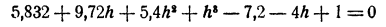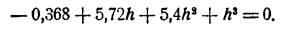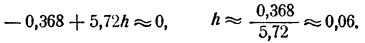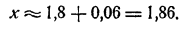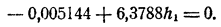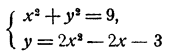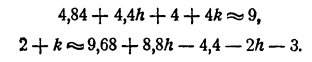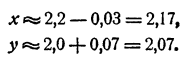Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Системы уравнений высших степеней в математике с примерами решения и образцами выполнения
Системы двух уравнений первой и второй степени с двумя неизвестными:
Общий вид многочлена второй степени от двух переменных у и x, очевидно, следующий:
где а, b, с, d, е, f—данные числа. Общий вид системы уравнений с двумя неизвестными, состоящей из одного уравнения первой степени и одного уравнения второй степени, следующий:
Система такого вида легко решается способом подстановки. Именно, из второго уравнения можно выразить одно из неизвестных через другое и затем подставить в первое уравнение. В результате этого первое уравнение превратится в уравнение с одним неизвестным, вообще говоря, квадратное. Решив это уравнение, мы сможем определить затем и значения нового неизвестного.
При этом способе решения систем проверка полученных решений посредством подстановки в уравнение системы не обязательна и производится только для контроля правильности вычислений, ибо можно доказать, что при исключении одного неизвестного указанным способом лишних решений возникнуть не может.
Пример:
Решение:
Исключим из системы неизвестное у. С этой целью решим второе уравнение относительно у. Получим 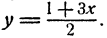
откуда после преобразований
и, следовательно, 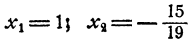
Ответ. Система имеет два решения
Тот же прием исключения следует применять при решении систем трех уравнений с тремя неизвестными, если два уравнения имеют первую степень, третье квадратное. При этом из двух уравнений первой степени нужно выразить два неизвестных через третье неизвестное, и полученные выражения подставить в уравнение второй степени.
Таким же образом можно поступать при решении систем я уравнений с п неизвестными при любом я, если все уравнения, кроме одного квадратного, имеют первую степень.
Пример:
Решение:
Перепишем два последних уравнения системы в виде
Решая эту систему относительно х и у по обычным правилам, получим
Подставив эти выражения в первое уравнение, получим
Остается определить соответствующие значения для х и у, что делается подстановкой значений z₁, и z₂ в выражении х и у через z. Мы получим два решения системы:
Системы уравнений, решаемые особыми приемами
В гл. II, § 9 мы рассматривали системы уравнений вида
которые легко решаются при помощи формул Виета. Но, конечно, можно решать такие системы и способом исключения, описанным в предыдущем параграфе.
Часто встречающиеся системы уравнений вида
легко решаются методом исключения, но их можно решать и иначе. Именно, возведя в квадрат второе уравнение и вычитая из него первое, мы получим новое уравнение
которое является следствием данной системы. Объединив его с уравнением
мы получим систему, решаемую при помощи формул Виета.
Пример:
Решение:
Если х и у удовлетворяют уравнениям системы, то 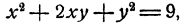
для которой получаем два решения
Оба они удовлетворяют уравнениям исходной системы.
Еще проще решаются системы вида
Действительно, х² — y² = (x — у)(х + у), и потому если допустить, что х и у удовлетворяют обоим уравнениям системы, то (х—у) b = а, и следовательно, 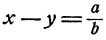
Пример:
Решение:
Если х и у удовлетворяют уравнениям системы, то
и следовательно, х + у =b. Решая систему
получим х = 4; v = 1.
Ответ. х = 4; v = 1.
Наконец отметим системы вида
Такие системы уравнений можно решить способом исключения, именно, в силу второго уравнения 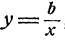
Однако здесь следует рекомендовать другой прием. Именно, если к первому уравнению добавить, а затем вычесть удвоенное второе, то мы получим новую систему
являющуюся следствием исходной.
Но новая система легко решается, ибо из нее следует, что
и система распадается на 4 системы уравнений первой степени
Следует отметить, что сопоставление результатов решения рассмотренной системы по способу исключения и при помощи указанного искусственного приема приводит к тем же соотношениям, которые были получены из сопоставления двух способов решения биквадратного уравнения.
Системы двух уравнений второй степени, не содержащие линейных членов
Решение системы двух уравнений второй степени с двумя неизвестными общего вида
представляет значительные трудности. Именно, можно доказать, что решение такой системы зачастую сводится к решению уравнения четвертой степени, а нахождение решения общего уравнения четвертой степени представляет довольно сложную задачу, не входящую в рамки курса элементарной алгебры.
Для некоторых систем частного вида возможно элементарное решение. Важным примером таких систем являются системы двух квадратных уравнений, каждое из которых не содержит членов первой степени относительно неизвестных, т. е. системы вида
В этом случае система решается посредством уничтожения свободных членов. Это делается так. Первое уравнение умножается на f₁ второе на f и полученные уравнения вычитаются. Составленное так новое уравнение является следствием исходной системы и имеет вид Ах²+Вху+Су² =0, из которого следует, что
(если только у ≠ 0), откуда мы можем определить отношение
Найдя это отношение, мы можем выразить х через у и затем подставить в одно из уравнений исходной системы. Получившееся в результате неполное квадратное уравнение относительно у легко решается.
Нетрудно видеть, что если А ≠ 0 и хотя бы один из свободных членов в исходных уравнениях отличен от 0, то сделанное выше предположение у ≠ 0 не нарушает общности.
Действительно, если в уравнении Ах² + Вху + Су² == 0 при А ≠ 0 положим у = 0, то и х = 0. Но x = 0; y = 0 не может быть решением исходной системы, если хотя бы один из ее свободных членов отличен от нуля.
Если же коэффициент А = 0, то решение вспомогательного уравнения Вху + Су² = 0 только упрощается, для решения достаточно вынести за скобку у и приравнять к нулю каждый множитель.
Пример:
Решение:
Умножив первое уравнение на 7 и второе на 3, получим после вычитания
Таким образом, х = 22у или х = 2у. Дальнейшее очевидно. Доведя решение до конца, получим четыре решения системы
Решение систем уравнений высших степеней
Задача о решении системы уравнений высших степеней с несколькими неизвестными в общем случае является очень трудной, часто не допускающей решения средствами элементарной алгебры. Однако во многих случаях, комбинируя известные методы решения уравнений и систем уравнений — метод сложения и вычитания, исключения неизвестного с помощью подстановки, введения нового неизвестного— удается найти путь к решению системы. Но в каждой отдельной задаче приходится использовать ее частные особенности для того, чтобы найти удачный метод решения. Рассмотрим несколько примеров.
Пример:
Решить систему уравнений.
Решение:
Способ 1. Из второго уравнения находим, что у = 3 — х. Подставив в первое уравнение, получаем
и, после упрощений,
Соответствующие значения для у будут такими:
Система имеет два решения.
Способ 2. Представим х³ + y³ = 18 как
Принимая во внимание второе уравнение, получим 27 — 9xy = 18, откуда ху = 1. Система
есть следствие исходной, но и исходная есть следствие преобразованной, ибо если х + у = 3; ху = 1, то
Решая преобразованную систему при помощи формул Виета, получим те же два решения:
Пример:
Решение:
Исключение одной из неизвестных величин приводит к решению уравнения четвертой степени, в котором все коэффициенты отличны от нуля. Поэтому лучше избежать этого пути. Это легко сделать, введя новую неизвестную z = xy. Тогда
Таким образом, для z получаем уравнение
откуда z₁ = 47; z₂ = 3.
Итак, данная система расщепилась на две системы:
первая из которых не имеет действительных решений, а вторая имеет следующие решения:
Указанный прием удобно применять к системам двух уравнений с двумя неизвестными, в случае если каждое из уравнений симметрично относительно х и у, т. е. если уравнения не изменяются при перемене х и у местами.
Пример:
Решить систему уравнений:
Решение:
Перемножив уравнения системы, получим
откуда xyz = ±30. Но так как ху = 5, то отсюда следует, что =5z±30 и z = ±6. Теперь х и у легко определить из второго и третьего уравнений системы. Мы приходим к двум решениям:
Пример:
Решить систему уравнений
Решение:
Возвысив обе части первого уравнения в квадрат, получим
Вычитая из этого уравнения второе уравнение данной системы, получим 2x³y³ = 686, откуда (xy)³ = 343; ху = 7. Теперь из первого уравнения данной системы находим, что 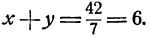
Пример:
Решить систему уравнений
Решение:
В первом уравнении раскроем скобки в каждом множителе. Затем поделим обе части обоих уравнений на ху. Получим
Теперь введем новые неизвестные 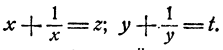
Эта система легко решается. Получаем:
Далее находим значения для х и у из уравнений
Всего получим восемь решений:
Многообразие приемов, которые могут применяться при решении систем уравнений высших степеней, неисчерпаемо, и тем не менее найти путь к решению данной системы удается далеко не всегда. Важно проявлять изобретательность при решении системы в тех случаях, когда это возможно.
Графическое решение уравнений с одним неизвестным
Как уже было сказано, алгебраические методы решения систем уравнений далеко не всегда применимы. Но для целей практики бывает важно находить решения систем уравнений хотя бы приближенно. Эта цель хорошо достигается применением графических методов. Сначала рассмотрим применение графиков к приближенному решению одного уравнения с одним неизвестным.
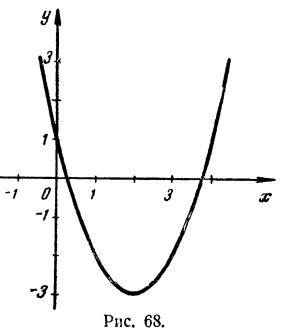
Пусть дано уравнение х²- 4x+1 = 0. Для того чтобы графически решить такое уравнение, рассматриваем неизвестное х как независимое переменное, а левую часть уравнения как функцию этой переменной, т. е. введем в рассмотрение функцию y = x²-4x+1
Решить предложенное уравнение — значит узнать, при каких значениях независимой переменной х функция у обращается в нуль.
Точки графика, соответствующие таким значениям независимой переменной, лежат на оси абсцисс, ибо ордината каждой такой точки равна нулю. Следовательно, интересующие нас точки графика являются точками пересечения графика с осью абсцисс, а корни уравнения x²-4x+1=0 являются абсциссами этих точек пересечения. При этом абсцисса каждой точки пересечения графика с осью абсцисс является корнем уравнения x²-4x+1=0
Строим график функции y = x²-4x+1 Он имеет вид параболы с вершиной в точке (2,-3) (рис. 68). По чертежу находим, что 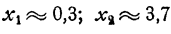
Совершенно такие же рассуждения можно применить к любому уравнению .у —0, где у есть алгебраическое выражение от неизвестной х. Именно, для графического решения такого уравнения нужно построить график выражения у, рассматриваемого как функция от переменной х, и найти точки пересечения этого графика с осью абсцисс. Абсциссы точек пересечения будут корнями уравнения. Конечно, при графическом решении уравнений корни получаются приближенно и довольно грубо, так как на чертеже произвести измерение абсцисс с высокой степенью точности невозможно.
Пример:
Решение:
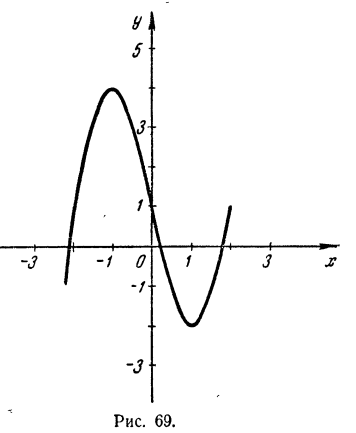
Строим график функции у = x³ — 4x + 1, вычислив предварительно таблицу значений:
По результатам этих вычислений мы видим, что при изменении х от —3 до —2 функция переходит от отрицательных значений к положительным, на участке от 0 до 1 переходит от положительных значений к отрицательным и на участке от 1 до 2 снова от отри-
нательных значений к положительным. На этих участках и следует ожидать, что график пересечет ось абсцисс.
Проводим вычисления для некоторых промежуточных значений х, взятых на этих участках с целью уточнения хода функции:
Теперь построим график по всем вычисленным точкам, соединив их плавной линией (рис. 69).
Из этого чертежа мы получаем:
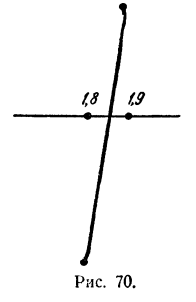
Для того чтобы уточнить значения корней, следует построить в бoльшем масштабе участки графика, примыкающие к корням, вычислив дополнительно значения функции на этих участках. Например, для уточнения корня х₃ проведем следующее вычисление:
Изобразим эти точки на чертеже, приняв большую единицу масштаба (рис. 70).
На таком малом участке изменения х мы вправе считать, что график очень близок к прямой линии. Исходя из этого предположения, получим
Графическое решение систем двух уравнений с двумя неизвестными
Пусть дана система уравнений с двумя неизвестными х и у. Каждое из этих уравнений, взятое отдельно, определяет зависимость между величинами х и у.
Построим на одном чертеже графики этих зависимостей. Числа (x₀y₀), образующие решение системы, должны удовлетворять обоим уравнениям системы, а следовательно, точка с координатами (х₀ у₀) должна лежать на графиках обеих зависимостей, т. е. должна являться точкой пересечения этих графиков.
Обратно, координаты (x₀у₀) любой точки пересечения построенных графиков удовлетворяют обоим уравнениям системы, т. е. образуют решение системы.
Таким образом, для того чтобы графически решить систему двух уравнений с двумя неизвестными, нужно построить график для каждого из уравнений и найти точки пересечения этих графиков. Координаты каждой точки пересечения образуют решение системы.
Пример:
Решить графически систему уравнений
Решение:
Алгебраическое решение этой системы затруднительно. Хотя неизвестное у и легко исключается посредством подстановки в первое уравнение его выражения через дг из второго уравнения, но в результате такого исключения получается уравнение четвертой степени относительно х, решение которого выходит за рамки элементарного курса алгебры.
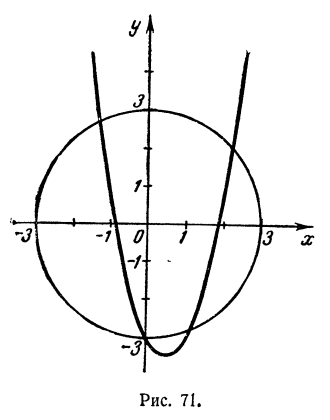
Обратимся к построению графиков. Графиком зависимости х² + у² = 9 является, как мы видели (гл. III, § 3, третий пример), окружность с центром в начале координат и радиусом, равным 3. Графиком зависимости у= 2х² — 2х — 3 является парабола, которую легко построить по таблице значений (рис. 71). Графики пересекаются в четырех точках, координаты которых суть приближенно (—1,2; 2,7); (0; —3); (1,1; —2,8) и (2,2: 2,0).
Следовательно, данная система имеет четыре решения
Второе решение оказывается точным. Остальные три — приближенные.
Графическое решение системы двух уравнений с двумя неизвестными почти не сложнее графического решения одного уравнения с одним неизвестным, а иногда даже проще.
Поэтому часто бывает полезно преобразовать посредством введения нового неизвестного одно уравнение с одним неизвестным в систему двух уравнений с двумя неизвестными, а затем решать эту систему графически. При таком преобразовании следует заботиться о том, чтобы построение графиков обоих уравнений полученной системы было как можно проще.
Рассмотрим несколько примеров на применение этого приема.
Пример:
Решить графически уравнение
Решение:
Представим предложенное уравнение в виде x²=x+1. Мы видим, что в левой и правой частях уравнения находятся некоторые функции от х. Решить уравнение — значит найти, при каких значениях независимого параметра обе функции принимают равные значения. Графически это означает, что нужно найти абсциссы точек пересечения графиков функций у = х² и у =х 1.
Действительно, если при х = а а² = а + 1, то это значит, что точка (а, а²) совпадает с точкой (a, a+1) и, следовательно, принадлежит как графику функции у = х², так и графику функции у = х + 1.
Очевидно и обратное. Если графики функций у = х² и у = x + 1 пересекаются в точке (а, b), то b = a² = a + 1 и, следовательно, при х = а обе функции принимают равные значения. Все сказанное можно коротко изложить так.
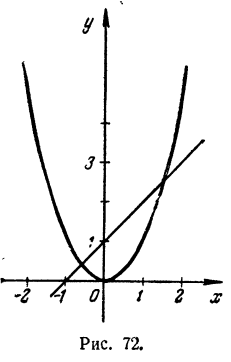
Вводим новую неизвестную y = х². Тогда данное уравнение переходит в уравнение у — х—1= 0, которое вместе с введенной зависимостью дает систему
Графиком зависимости у = х² является .парабола, графиком зависимости у = х + 1— прямая линия (рис. 72). Решение задачи дают абсциссы точек пересечения. Они равны приближенно:
Любое приведенное квадратное уравнение х² + рх + q = 0 может быть решено тем же образом, посредством преобразования в систему
Это удобно тем, что графиком первой зависимости является одна и та же парабола, а графиком второй зависимости является прямая линия, которую очень легко построить в каждом частном случае по двум точкам. Поэтому, тщательно построив в большом масштабе параболу у=х3, мы получаем возможность быстро решать любое приведенное квадратное уравнение.
Подобным образом для решения кубического уравнения, имеющего вид х³ + рх + q = 0, достаточно заготовить график функции у = х³. Абсциссы точек пересечения этого графика с прямой у + рх + q = 0 дают корни уравнения x³ + + q = 0.
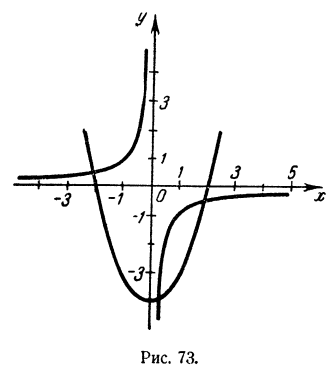
Пример:
Превратив в систему, решить графически уравнение
Решение:
Это делают приемом, указанным выше. Однако это можно сделать и иначе. Именно, перепишем уравнение в виде х(х² — 4)+1=0
и положим х² — 4 = у. Уравнение заменится системой
Графиком первого уравнения системы является парабола, графиком второго — гипербола (рис. 73). Абсциссы точек пересечения суть
Этим приемом можно решить любое кубическое уравнение
Графиком первого уравнения является парабола, графиком второго — гипербола.
Решение уравнения четвертой степени ах⁴ + bх² + сх + d = 0 при с ≠ 0 легко сводится к определению точки пересечения двух парабол.
Для этого вводим новое неизвестное у = х² У и уравнение заменяем системой
Графиком первого уравнения является парабола с вершиной в начале координат и осью, совпадающей с осью ординат. Графиком второго уравнения тоже является парабола, но только ее ось параллельна оси абсцисс. Действительно, решив второе уравнение относительно х, мы получим
т. с. х является квадратичной функцией от у, графиком которой является парабола с осью, параллельной оси абсцисс.
Из рассмотренных примеров ясно, что каждое данное уравнение с одним неизвестным можно преобразовать а систему двух уравнений с двумя неизвестными многими способами и при выборе какого-нибудь способа следует заботиться о наиболее выгодном расположении графиков на чертеже.
Уточнение корня уравнения или решения системы нелинейных уравнений, исходя из грубого приближения
При графическом решении корень уравнения или решение системы уравнение определяется лишь грубо приближенно. Уточнение результата за счет увеличения масштаба не очень эффективно, так как повышение точности требует пропорционального увеличения масштаба. Например, чтобы определить новую значащую цифру после занятой в десятичном разложении корня, т. е. увеличить точность в 10 раз, нужно и масштаб увеличить в 10 раз.
Однако существует весьма хорошо действующий алгебраический способ для подобного рода уточнения. Мы не будем излагать его в общем виде, а ограничимся только рассмотрением примеров его применения.
Пример:
Для уравнения x³ — 4x + 1= 0 известно приближенное значение одного из корней х ≈1,8. Требуется вычислить этот корень с большей точностью.
Решение:
Поступаем так. Положим x =1,8 + h, где h — новая неизвестная. Мы можем быть уверены, что h есть маленькое число, во всяком случае меньшее, чем 0,1. Подставив в уравнение вместо х его выражение через h, получим
Так как h² меньше h во столько же раз, во сколько h меньше единицы, для приближенного вычисления h отбросим в полученном уравнении члены с h² и h³. Получим
Для дальнейшего уточнения мы можем еще раз применить тот лее прием. Положим x≈1,86 + h₁,. Для h₁ получим, отбрасывая члены, содержащие h₁² и h₁³, приближенное уравнение
(При этом нет надобности вычислять коэффициенты при h₁² и h₁³ , ибо соответствующие члены мы все равно отбрасываем.) Отсюда h≈ 0,0008 и, следовательно,x ≈ 1,8608.
Продолжая этот прием, мы можем получить значение корня уравнения с любой степенью точности.
В общем виде идея метода такова. Если х₀ есть приближенное значение корня данного уравнения, мы полагаем в уравнении x= x₀ + h и в полученном уравнении относительно h отбрасываем члены, содержащие h выше, чем в первой степени, и решаем приближенно получившееся уравнение первой степени относительно h. Тогда число x₁ = x₀ + h оказывается, вообще говоря, значительно лучшим приближением к корню, чем исходное приближение х₀. В случае надобности процесс можно повторить.
Пример:
Для одного решения системы уравнений
известны приближенные значения х ≈ 2,2, у ≈ 2,0. Найти решение с большей точностью.
Решение:
Будем действовать тем же способом, как при уточнении корня одного уравнения с одним неизвестным. Именно, положим x = 2,2 + h; .у = 2,0 + к и, подставив в уравнение, отбросим все члены, содержащие h², k², hk, так как эти величины значительно меньше самих h и k. Получим
Решив эту систему, получим h ≈ — 0,03, k ≈ 0,07. Таким образом, уточненными значениями для х и у являются значения
Для дальнейшего уточнения можно повторить тот же процесс.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Об уравнениях высших степеней
Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.
Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:

В этой статье я рассмотрю:
1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.
Кубические уравнения
Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:
Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:
В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.
Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.
Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.
Возвратные кубические уравнения
Возвратные кубические уравнения имеют вид:
Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:
Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.
Теорема Безу и схема Горнера
Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:
Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.
Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.
Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:
И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:
(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:
Возвратные биквадратные уравнения
Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:
В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:
Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы.
Уберём -2 из скобки, предварительно домножив его на a, после чего вводим новую переменную, t и получаем квадратное уравнение.
А теперь перейдём к примеру:
Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).
Область применения
В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.
http://lfirmal.com/sistemy-uravneniy-vysshih-stepeney/
http://habr.com/ru/post/484902/