Дифференциальные уравнения конвективного теплообмена. Основные понятия конвективного теплообмена
Основные понятия конвективного теплообмена
Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом перенос теплоты осуществляется одновременно конвекцией и теплопроводностью.
Если в единицу времени через единицу контрольной поверхности нормально к ней проходит масса жидкости 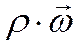
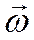
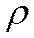
Конвекция теплоты всегда сопровождается теплопроводностью, т.к. при движении жидкости или газа происходит соприкосновение отдельных частиц, имеющих различные температуры. В результате конвективный теплообмен описывают уравнением
При расчетах конвективного теплообмена между текущей жидкостью и твёрдой стенкой используют закон Ньютона – Рихмана
Коэффициент теплоотдачи α зависит от большого количества факторов. В общем случае α является функцией
— формы и размеров тела,
— скорости и температуры жидкости,
— физических параметров жидкости,
Чтобы привести жидкость в движение, к ней необходимо приложить силу. Силы, действующие на какой-либо элемент жидкости, можно разделить на массовые (или объемные) и поверхностные.
Массовыми называют силы, приложенные ко всем частицам жидкости и обусловленные внешними силовыми полями (например, гравитационным или электрическим).
Поверхностные силы возникают вследствие действия окружающей жидкости или твердых тел; они приложены к поверхности контрольного объема жидкости. Такими силами являются силы внешнего давления и силы трения.
Различают свободную и вынужденную конвекцию.
В первом случае жидкость с неоднородным распределением температуры, и, как следствие, с неоднородным распределением плотности, находится в поле земного тяготения. Поэтому в ней может возникнуть свободное гравитационное движение.
Вынужденное движение объема жидкости происходит под действием внешних поверхностных сил, приложенных на его границах, за счет предварительно сообщенной кинетической энергии (например, за счет работы насоса, вентилятора, ветра).
Вынужденное движение в общем случае может сопровождаться свободным движением. Относительное влияние последнего тем больше, чем больше разница температур отдельных частиц среды и чем меньше скорость вынужденного движения.
Дифференциальные уравнения конвективного теплообмена
Из уравнения 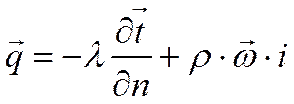
Связь между температурой и энтальпией может быть установлена следующим образом. Для реальной жидкости 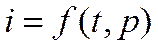
Отсюда
Для многих задач в предположении о несжимаемости жидкости (ρ=const) с достаточной степенью точности можно принять 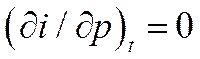
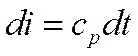
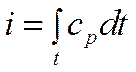
Выведем дифференциальное уравнение, описывающее температурное поле в движущейся жидкости.
При выводе будем полагать, что
— её физические параметры постоянны,
— энергия деформации мала по сравнению с изменением внутренней энергии.
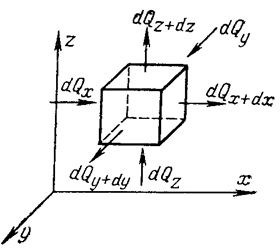
Через грани параллелепипеда теплота переносится теплопроводностью и конвекцией; в общем случае в рассматриваемом объеме может выделяться теплота внутренними источниками.
Вывод уравнения энергии, соответствующего принятым здесь условиям, был получен ранее:
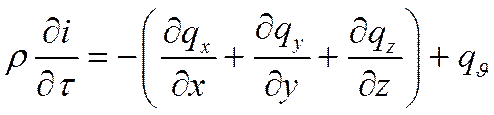
Проекции плотности теплового потока 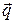
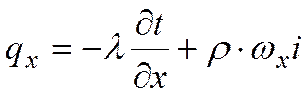
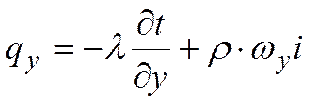
Подставляя значения qx,qy и qz в уравнение Фурье, можно получить
Для несжимаемых жидкостей (ρ=const) из закона сохранения массы следует:
Тогда,
или, если 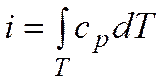
Последнее уравнение является уравнением энергии, описывающим распределение температур внутри движущейся жидкости.
Если 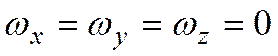
Как следует из уравнения энергии, температурное поле в движущейся жидкости зависит от составляющих скорости 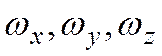
Чтобы сделать систему уравнений замкнутой, необходимо добавить уравнения, которые бы описывали изменение скорости во времени и пространстве. Такими уравнениями являются дифференциальные уравнения движения.
Уравнение движения вдоль оси Ох
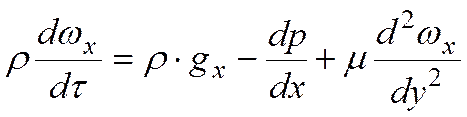
Описание движения жидкости усложняется, если скорость изменяется по трем направлениям.
для оси Ох
для оси Оу
для оси Оz
В общем случае составляющие скорости 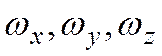
На основании понятия о полной (субстанциальной) производной для оси Ох имеем
Аналогичные уравнения можно записать и для осей Оу, Оz.
Используя векторную форму записи:
Уравнение движения получено без учета зависимости физических параметров жидкости от температуры. В частности, не учтена зависимость плотности от температуры.
В то же время свободное движение жидкости определяется разностью плотностей холодных и нагретых частиц жидкости.
Приближенный учет переменности плотности возможен с введением температурного коэффициента объемного расширения β.
Т.к. в уравнение движения, помимо 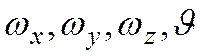
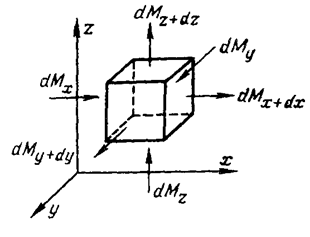
В направлении оси Ох в параллелепипед втекает масса жидкости
Величина 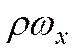
Ограничиваясь первыми двумя членами разложения в ряд, получаем, что масса dMx+dx, вытекающая из элементарного параллелепида в направлении оси Ох
Излишек массы жидкости, вытекающий из элементарного объема в направлении оси Ох
Аналогичным образом можно получить уравнения для направлений по осям Оу и Оz.
Полный избыток массы жидкости, вытекающей из элементарного объема в направлении всех трех осей обусловливается изменением плотности жидкости в объеме dυ и равен изменению массы данного объема во времени 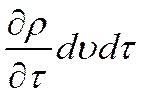
Произведя сокращение на dυ и dτ и перенеся все члены в левую часть равенства, окончательно получим дифференциальное уравнение сплошности для сжимаемых жидкостей
Для несжимаемых жидкостей, полагая ρ=const, получаем
Уравнение сплошности является уравнением сохранения массы.
| | | следующая лекция ==> | |
| Пути интенсификации теплопередачи | | | Критерии подобия и уравнения подобия |
Дата добавления: 2016-02-09 ; просмотров: 2731 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Система дифференциальных уравнений конвективного теплообмена
Для полного аналитического описания процесса конвективного теплообмена необходимо задать систему дифференциальных уравнений, выражающих законы сохранения массы (уравнение неразрывности, сплошности), импульса (уравнение движения), энергии (уравнение энергии), соответствующие специальные законы импульса и теплоты, зависимость физических свойств теплоносителя от температуры и давления и, наконец, условия однозначности, включающие начальные и граничные условия. В частности, для потока несжимаемой жидкости при условии, что вязкая диссипация (рассеяние) энергии пренебрежимо мала, эти уравнения имеют вид:
уравнение неразрывности 
 (13)
(13) (14)
(14)где через xj обозначены декартовы оси координат; 
В уравнениях (13) и (14) в качестве специальных законов переноса используются закон трения Ньютона

и закон теплопроводности Фурье

Система дифференциальных уравнений (12)-(14) справедлива для турбулентных течений только при условии, что под параметрами потока в этих уравнениях подразумеваются их актуальные (мгновенные) значения. Если в (12)-(14) ввести условие ∂/∂ 



Члены 

 |
 |
Формула (15.49) не учитывает волновой характер движения пленки, приводящий к увеличению теплоотдачи; это увеличение можно учесть
умножением Nu = l/ на Re0,04.
Конденсация пара на наружной поверхности горизонтальной трубы отличается от рассмотренного
случая тем, что направления силы тяжести и вектора скорости для пленки не совпадают. Расчет средней теплоотдачи можно производить по формуле (15.49), заменив коэффициент на 0,728 и взяв диаметр трубы в качестве определяющего размера. Кипение представляет собой процесс образования па — ра внутри жидкости, нагретой выше температуры насы — щения. Обычно необходимая для кипения теплота посту — пает в жидкость от поверхности нагрева, температура которой tc>tн. В этом случае на поверхности нагрева идет непрерывно возобновляемое образование паровых пузырей или паровой пленки.
На рис. 15.8 схематично представлена зависимость коэффициента теплоотдачи а на поверхности нагрева от температурного напора t=tc—tн. Участок АВ соответствует области свободного движения жидкости, при котором возникновение пузырей возможно, но происходит весьма вяло. Для воды при атмосферном давлении параметры точки В примерно равны: а = 1000 Вт/(м2К), t = 5 К. Участок ВК соответствует развитому пузырьковому режиму кипения, при котором интенсивно образующиеся пузыри разрушают вязкий подслой на стенке и обеспечивают высокие значения коэффициента теплоотдачи. Аналогичные приведенным выше параметры точки К равны: кр=50 000 Вт/(м2К), tкр = 25 К. В точке К интенсивность образования пара становится больше возможной скорости его отвода от поверхности нагрева. Происходит кризис теплоотдачи при кипении, сопровождающийся резким ухудшением теплоотдачи (величина а в точках С, С1 и D примерно такая же, как в точке В). Если тепловой поток на поверхности нагрева при переходе через точку К не изменяется, то осуществляется скач
кообразный переход по линии КС1, при этом температурный напор возрастает до значения 103 К и происходит разрушение поверхностей нагрева (например, труб парогенератора в топке). Ухудшение теплоотдачи объясняется возникновением низкотеплопроводной паровой прослойки между поверхностью нагрева и жидкостью, например, при 100 °С теплопроводность водяного пара примерно в 29 раз меньше теплопроводности воды. Участок CD соответствует пленочному режиму кипения, а линия СК\ — обратному переходу от пленочного режима к пузырьковому. Участку КС отвечает так называемый переходный режим, при котором на поверхности реализуются в различных местах оба режима.
С практической точки зрения важно организовать кипение в области пузырькового режима с высокими значениями а, причем так, чтобы не допустить возникновения кризиса.
Теоретический анализ показывает, что пузырьки пара образуются в микроскопических углублениях на поверхности нагрева, которая чаще всего является металлической. Основными факторами, от которых зависит теплоотдача при кипении, являются критический радиус пузыря и частота отрыва пузырей от поверхности нагрева. Критический радиус Rкр определяется условиями термодинамического равновесия фаз, которые представлены, например, выражениями (4.37) — (4.39). В данном случае необходимо учесть кривизну поверхности пузыря и связанное с этим дополнительное давление p = 2R, где R—радиус пузыря, а о — поверхностное натяжение. Условие (4.39) поэтому примет вид р»=р’+ 2/Rкр, откуда
Внутри пузыря находится насыщенный пар, поэтому t» = tn<p«)- Согласно условию термического равновесия фаз (4.38) должно быть t» — t‘, поэтому жидкость вокруг пузыря находится в перегретом состоянии, т. е. t‘> >tн(р’). Отметим, что давление р’ определяется внешними условиями, это — атмосферное давление, давление в парогенераторе и т. п.
Жизнеспособные пузыри возникают только в углублениях с радиусом R>Rкр. В этом случае рпара 0 и -> ¥ плотность потока излучения стремится к нулю.
что позволяет экспоненциальную функцию в уравнении (16.3) представить в виде ряда:
Закон Планка имеет два предельных случая. Первый предельный случай относится к области больших длин волн при высоких значениях температур. В этом случае
Условие (16.4) позволяет ограничиться двумя членами этого ряда. Подставляя эти члены в формулу (16.3) вместо экспоненциальной функции, получим:
Зависимость (16.5) выражает закон Релея — Джинса, являющийся частным случаем закона Планка.
Второй предельный случай закона Планка соответствует коротковолновой области спектра при высоких температурах, где С2.
Тогда в уравнении (16.3) можно пренебречь единицей по сравнению с членом С2/Т и получить следующую приближенную формулу:
Зависимость (16.6) известна как закон Вина
Положения максимумов излучения (см. рис. 16.3) можно получить из. выражения (16.3), исследуя функцию на экстремум. Приравнивая производную нулю и находя значение = mах, при котором E достигает экстремального значения,
где max — длина волны, м, которой соответствует максимальная плотность излучения.
Зависимость (16.7) выражает закон смещения Вина для абсолютно черного тела. Согласно этому закону максимальное значение спектральной плотности потока излучения с повышением температуры сдвигается в сторону более коротких волн.
Закон Стефана — Больцмана устанавливает зависимость плотности интегрального полусферического излучения * от температуры абсолютно черного тела и может быть получен из формулы Планка. Интегрируя выражение (16.3) во всем интервале длин волн, получим:
где =5,67*10-8 Вт/(м2*К4)—постоянная Стефана — Больцмана. Согласно уравнению (16.8), плотность интегрального полусферического излучения абсолютно черного тела зависит только от температуры и изменяется пропорционально четвертой степени абсолютной температуры. При высоких температурах величина Г4 достигает больших значений, поэтому для удобства практических расчетов формулу (16.8) записывают в виде:
где С0=*108=5,67 Вт/(м2*К4)


Закон Стефана — Больцмана позволяет определить суммарное излучение поверхности тела по всем направлениям в пределах полусферы.
Энергия излучения, испускаемая телом по отдельным направлениям, устанавливается законом Ламберта. Согласно закону Ламберта, поток излучения абсолютно черного тела в данном направлении пропорционален потоку излучения в направлении нормали к поверхности и косинусу угла между ними. Для интенсивности излучения закон Ламберта
где I и In — интенсивности интегрального излучения в направлении, определяемом углом T2. Обе плоскости излучают в пространство энергию, которая частично поглощается и отражается самими плоскостями, при этом процессы поглощения и отражения многократно повторяются. Воспользовавшись понятиями эффективного потока, запишем для результирующей плотности, полусферического излучения Eрез от первого тела ко второму:
Согласно зависимости (16.1), эффективную излуча-тельную способность Eэф1 и Eэф2 каждой плоскости можно представить
При составлении зависимостей (16.16) предполагалось, что Eпад1=Eэф2; Eпад2=Eэф1. Решим систему урав-
нений (16.16)
Подставив значения Eэф1и Eэф2 в уравнение (16.15), получим:

Тепловой поток q, переносимый излучением от первой плоскости ко второй, найдем из уравнений (16.12), (16.14) и (16.17)

где пр — приведенная степень черноты системы, определяемая формулой

Из формулы (16.19) следует, что если одна из плоскостей обладает значительной степенью черноты по сравнению с другой: 1>>2, то пр определяется величиной меньшей степени черноты: пр=2. Для тел с большой степенью черноты (1 и 2 не менее 0,8) пр приближенно может быть принята равной 12.
Рассмотрим теплообмен между телом и его оболочкой. На рис. 16.4,а, б представлены следующие системы двух тел: тело 1 находится в замкнутой полости тела 2, тело 2 охватывает плоское или выпуклое тело 1.
Пусть тело 1 имеет более высокую температуру, тогда теплообмен излучением между телами 1 и 2 приведет к переносу тепловой энергии от тела 1 к телу .2. Результирующая плотность полусферического излучения в рассматриваемом случае может быть найдена изложенным выше методом. Однако в отличие от предыдущей задачи необходимо учесть, что не весь лучистый поток с тела 1 попадает на тело 2 (см. рис. 16.4).
Введем понятие угловых коэффициентов излучения j1,2 и 2,1 Они показывают, какая часть лучистого потока, испускаемого одним телом, падает на другое тело, находящееся в лучистом теплообмене с первым, т. е.
ч
Результирующий тепловой поток Q1,2 может быть представлен в следующем виде:
Для случаев, изображенных на рис. 16.4, 2,1 =0,8. Требуется определить результирующий тепловой поток.
Выделим на каждом из рассматриваемых тел элементарные площадки dF1 и dF2, бесконечно малые по сравнению с расстоянием r между ними; введем углы 1 и 2 между линией, соединяющей середины элементарных площадок, и нормалями n1 и п2 к площадкам (рис. 16.5). Вычисления приводят к следующему выражению для Q1,2 •!•
имеет единицу площади и называется взаимной поверхностью излучения тел 1 и 2.
Можно показать, что величина Н1,2 связана с угловыми коэффициентами излучения 1,2 и 2,1 простыми
соотношениями: Н1,2 = 1,2F1; Н2,1 = 2,1F2; Н1,2 = H2,1 .
Следовательно, задача вычисления результирующего теплового потока Q1,2 между двумя произвольно расположенными в пространстве поверхностями конечных размеров сводится к определению коэффициента 1,2.
Угловые коэффициенты излучения характеризуют геометрические свойства различных систем тел, в которых рассматривается теплообмен излучением. При расчетах коэффициентов излучения ij или взаимных поверхностей излучения Hij часто используют метод лучистой (поточной) алгебры, базирующийся на некоторых общих свойствах лучистых потоков.
Рассмотрим теплообмен излучением при наличии экранов. Экраны уменьшают теплообмен излучением между телами, они устанавливаются ортогонально к направлению потока излучения и выполняются из тонких металлических листов.
Рассмотрим теплообмен излучением между двумя параллельными стенками, между которыми расположен экран (рис. 16.6). Тепловой поток можно определить из выражения (16.18). Примем C1 = C2=Cэ=C. Если экрана нет, то

При наличии экрана тепловой поток между первой стенкой и экраном выразится формулой

От экрана ко второй стенке передается теплота
При одинаковых
Из условия стационарности q1э=q2э=qэ. Приравнивая правые части равенств (16.25) и (16.26), определим. (Tэ/100)4=l/2[(T1/100)4+(T2/100)4].
Подставив (Tэ/100)4 в уравнение (16.25) или (16.26),
получим
Сопоставление формулы (16.27) с формулой (16.24), в которой C1,2=Cпр, показывает, что постановка экрана с таким же коэффициентом излучения, как у стенок, приводит к уменьшению теплового потока в 2 раза. Аналогично можно показать, что при п экранах тепловой поток уменьшится в n+1 раз. Таким образом, при одинаковых коэффициентах
Если коэффициенты излучения экрана и стенок неодинаковы (С1 С2 Сэ), то при одном экране
Здесь С1э С2э С1,2. Эти коэффициенты определяются по формуле приведенного коэффициента излучения. С помощью формулы (16.29) легко показать, что при уменьшении Сэ повышается эффективность экрана. Так, при Сэ=0,3 и С1 = С2 = 5,25 один экран уменьшает поток теплоты в 30 раз.
Повышение эффективности экрана при уменьшении коэффициента излучения обусловлено повышением его отражательной способности (так как С=АС0, a A+R = = 1). Но уменьшение потока теплоты обусловлено не только отражением экрана, но и тем, что благодаря экрану уменьшается перепад температур, определяющий тепловой поток. В самом деле,
Поэтому даже при С1 = С2=Сэ=С0, т. е. когда экран ничего не отражает, благодаря условию (16.29′) всегда qэ ¥, то теплота переносится только теплопроводностью, N ->0 — только излучением. Радиа-ционно-кондуктивный: теплообмен является весьма слож-
ным видом теплообмена. Сравнительно простые решения задачи получаются лишь для некоторых частных случаев.
При оптически тонком слое (kl = 0) излучение не поглощается в среде, а переносится от одной поверхности к другой, как в случае диатермичной среды. Полный тепловой поток определяется простым суммированием лучистого и кондуктивного потоков
При оптически толстом слое (kl->¥) влияние радиационных свойств поверхностей простирается в глубь объема, а характеристики излучения в любой точке объема зависят лишь от условий в непосредственной близости от этой точки. В этом случае полный тепловой поток складывается иначе, чем в уравнении (16.33), радиационный поток несколько видоизменен:
Радиационно-конвективный теплообмен весьма сложен в физическом отношении и описывается довольно сложной системой уравнений. Эти два обстоятельства затрудняют как аналитические, так и экспериментальные исследования сложного теплообмена, в связи с чем задача его инженерного расчета еще далека от своего решения. Для практических расчетов обычно используют принцип независимости конвективного и лучистого потоков, что оказывается достаточно верным, если один из них значительно меньше другого. Так, для учета теплоотдачи излучением к коэффициенту теплоотдачи конвекцией, подсчитанному обычным образом, т. е. без учета влияния радиационного теплообмена на профили скорости и температуры, рекомендуется прибавлять условный коэффициент теплоотдачи излучением л, поэтому суммарный коэффициент теплоотдачи равен = к+л.
Для сложных процессов теплообмена используют ряд чисел подобия, в частности числа Больцмана — Во и Кирпичева — Ki, имеющие вид:
Число Больцмана Во характеризует радиационно-конвективный теплообмен: чем оно меньше, тем большую роль играет лучистый теплообмен в среде по
сравнению с конвективным. Число Кирпичева Ki характеризует радиационно-кондуктивный теплообмен. Число Бугера Вu=kl0 характеризует оптическую плотность среды, т. е. прохождение через нее лучистой энергии.
ГЛАВА 17. ТЕПЛООБМЕННЫЕ АППАРАТЫ
§ 62. Классификация теплообменных аппаратов
Теплообменными аппаратами (теплообменниками) называют устройства, предназначенные для передачи теплоты от одной среды к другой при осуществлении различных тепловых процессов (например, нагревания, охлаждения, кипения, конденсации). Жидкие среды, воспринимающие или отдающие теплоту, именуют горячими или холодными теплоносителями.
По принципу действия теплообменные аппараты разделяются на поверхностные (рекуперативные и регенеративные), в которых тепловой перенос осуществляется с использованием разделяющих поверхностей и твердых тел, и смесительные, процессы нагревания и охлаждения в которых происходят при непосредственном контакте теплоносителей.
В рекуперативных теплообменниках горячий и холодный теплоносители перемещаются одновременно, а теплота непрерывно передается через разделяющую их стенку.
Регенеративными (регенераторами) называются теплообменные аппараты, в которых теплоносители попеременно соприкасаются с поверхностью так называемой насадки, аккумулирующей теплоту от горячего теплоносителя и отдающей ее холодному теплоносителю. Таким образом, для регенераторов характерен нестационарный теплообмен.
В зависимости от агрегатного состояния теплоносителей рекуперативные теплообменники классифицируются на газогазовые, газожидкостные, парогазовые, па-рожидкостные и жидкостножидкостные. В основу классификации рекуперативных теплообменников может быть также положен способ компоновки теплопередаю-щей поверхности или ее конфигурация: теплообменники типа «труба в трубе», кожухотрубчатые, с прямыми трубками, змеевиковые, пластинчатые, ребристые.
По относительному движению потоков теплоносителей теплообменники делят на прямоточные, противоточ-ные и со смешанным током.
В особую группу выделяют теплообменные аппараты с внутренними источниками теплоты, отвод которой осуществляется одним теплоносителем. Примером таких теплообменников могут служить электронагреватели, ядерные реакторы и др.
В связи с широким использованием теплообменников в различных областях техники возросло число их наименований, определяемых спецификой работы этих устройств. Так, встречаются парогенераторы, экономайзеры, воздушные калориферы, конвекторы, холодильники, конденсаторы, градирни, испарители, скрубберы, охладители выпара и т. д. Но несмотря на различное функциональное назначение этих аппаратов, методика теплового расчета является для них общей.
§ 63. Тепловой расчет рекуперативных теплообменников
При проектировании новых теплообменных аппаратов необходимо выполнить конструкторский тепловой расчет, целью которого является определение площади поверхности теплообмена, обеспечивающей передачу заданного количества теплоты от одного теплоносителя к другому. Для выявления возможности использования имеющихся аппаратов в тех или иных целях производят поверочный тепловой расчет, определяя конечные температуры теплоносителей t«г и t«x и количество переданной теплоты.
Основными расчетными уравнениями, записанными в дифференциальной форме, являются уравнение теплопередачи для элемента площади поверхности теплообмена dF:
и уравнение теплового баланса:
где Мг, Мх — массовые расходы горячего и холодного теплоносителей, кг/с; hг, hx — энтальпии теплоносителей, кДж/кг; dQпот — потери в окружающую среду, кВт.
В общем случае температуры теплоносителей в теплообменнике изменяются, изменяется и температурный
напор t = tг— tx. В расчетах используется среднее по всей площади поверхности теплообмена значение температурного напора tcp. В этом случае уравнение теплопередачи (17.1) записывается в виде (k=const):
Удельные изобарные теплоемкости ср теплоносителей зависят от температуры. Если использовать среднее значение изобарной теплоемкости в интервале температур от t‘ (вход) до t« (выход) и пренебречь потерями теплоты в окружающую среду Qпот, то уравнение (17.2) преобразуется
Произведение Mcp является полной теплоемкостью массового расхода теплоносителя в единицу времени и измеряется в Вт/К. Эта величина часто называется водяным эквивалентом.
Уравнение (17.4) при введении в него полных теп-лоемкостей W примет вид:
Соотношение (17.6) может быть записано для элемента площади поверхности теплообмена dF: Wx/Wг= =dtг/dtx.
Таким образом, отношение изменения температур теплоносителей обратно пропорционально отношению полных теплоёмкостей массовых расходов. На характер изменения температур теплоносителей вдоль по-верхности теплообмена, а значит и на температурный напор, значительное влияние оказывает схема движе-ния (рис. 17.1). При прямоточной схеме теплоносители движутся параллельно и в одном направлении (рис. 17.1,а). При параллельном, но противоположном направлении движения теплоносителей схема называется противотоком (рис: 17.1,6). Если теплоносители движутся во взаимно перпендикулярных направлениях, то схема их движения называется перекрестным током (рис. 17.1,в). На практике приходится осуществлять и более сложные схемы движений: многократный перекрестный ток, одновременный прямоток и противоток
(рис. 17.1,г) и т. д. При этом один или оба потока могут перемешиваться по своему сечению или же протекать по изолированным каналам.
На рис. 17.2 изображены характерные кривые изменения температуры вдоль поверхности теплообмена F для прямотока и противотока в зависимости от соотношений полных теплоемкостей Wг и Wx. На графиках, как следует из уравнения (17.6), меньшее изменение температуры получается для того теплоносителя, у которого полная теплоемкость массового расхода больше.
В случаях, когда один из теплоносителей имеет постоянную температуру (кипение жидкости или конденсация пара), прямоток и противоток равнозначны и среднее значение температурного напора не зависит от схемы движения потоков.
Рассмотрим теплообменный аппарат, работающий по противоточной схеме. Характер изменения темпера-
тур теплоносителей в этом теплообменнике показан на рис. 17.3.
При передаче теплоты dQ через элемент площади поверхности dF температура горячего теплоносителя снижается
а холодного возрастает на величину
Так как
Считая коэффициент теплопередачи k постоянным вдоль всей поверхности нагрева, интегрируем уравнение
или 
Если сравнить уравнение (17.8) с уравнением (17.3), то получаем
Обычно при расчете теплообменников формула (17.9) используется в виде
где tб и tм — наибольшая и наименьшая разности температур для данного теплообменного аппарата.
В формулу (17.10) введена поправка t учитывающая снижение среднего температурного напора для
теплообменников с перекрестным и смешанным токами по сравнению с теплообменниками с противотоком. Величина t зависит от значений вспомогательных характеристик P=(t«x—t‘x)/(t‘г-t»г) и R=(t‘г—
На рис. 17.4 представлены кривые, позволяющие определить поправку t для теплообменника, у которого схема движения теплоносителей более сложна, чем противоток и прямоток.
Рассчитанная по формуле (17.10) средняя разность температур называется среднелогарифмическим температурным напором и применяется для различных схем аппаратов при постоянстве массовых расходов теплоносителей.
Вместо среднелогарифмического температурного напора в расчетах может быть использован среднеарифметический напор
если tб/tм Wx величина At возрастает в том же направлении.
Для расчета конечных температур теплоносителей при
Для прямотока применимы такие формулы: и
зависят только от заданных величин, т. е. от kF/Wг и Wг/Wx. Они могут быть затабулированы, что значительно облегчает решение поставленной задачи.
Рассмотрим частные случаи для противоточного теплообменника. Если Wг=Wх=W, т. е. полные теплоемкости массовых расходов теплоносителей численно равны, то уравнения (17.20) и (17.21) для прямотока трансформируются
Для противотока
В случаях, когда температура одного из теплоносителей остается постоянной вдоль поверхности теплообмена, т. е. прямоточная и противоточная схемы равноценны, получаем:


§ 65. Сравнение прямоточной и противоточной схем движения теплоносителей
Анализ рис. 17.2 позволяет выявить одно важное преимущество противоточной схемы: конечная температура холодного теплоносителя t«x может быть более высокой, чем температура горячего теплоносителя на выходе из теплообменника. Такая ситуация невозможна в прямоточном теплообменнике, где всегда t«г>t«х-Лишь при бесконечно большой площади поверхности теплообмена на выходе из идеализированного прямоточного теплообменника можно получить равные температуры теплоносителей.
Вторым важным достоинством противоточной схемы является то, что средний температурный напор получается большим, чем для тех же температур при прямоточной схеме. Это значит, что при противоточном движении теплоносителей можно уменьшить площадь поверхности теплообмена [см. уравнение (17.3)].
Сравнение двух схем движения теплоносителей может быть., проведено путем сопоставления количества теплоты Qп, передаваемой при прямоточной схеме, и количества теплоты Qпр, передаваемой при противоточной схеме, при равенстве прочих условий.
На рис. 17.5 показана зависимость отношения Qп/Qпр от двух безразмерных характеристик Wг/Wx и kF/Wг. Равноценность двух схем наблюдается в случае, когда полная теплоемкость одного из тепдоносителей значительно больше полной теплоемкости другого (Wг/Wx>15 или Wг/Wx 1. При tг = tx существует равновесие между двумя потоками теплоносителей; линия, выражающая это равновесие, также представлена на рис. 17.7, она проходит через начало координат.
Из определения
Решая совместно уравнения (17.33) и (17.1), получаем
Интегрирование этого выражения в пределах температур входа и выхода горячей жидкости приводит к следующему уравнению:
В соответствии с рис. 17.7 можно получить равенства:
Таким
Решая совместно уравнения (17.36) и (17.38), получаем окончательно
По этому уравнению построен график на рис. 17.6.
Анализ зависимости =f(N) для противоточного теплообменника приведен выше. Следует добавить, что меньшее соотношение полных теплоемкостей теплоносителей позволяет получить большую эффективность при заданном значении N.
На практике встречаются два предельных вида уравнения (17.39). Если в процессе передачи теплоты одна из жидкостей остается при постоянной температуре (кипение или конденсация), то ее полная теплоемкость бесконечно велика, т. е. Wmin/Wmax= 0 и при этом
Если при расчете теплообменника требуется определить необходимую площадь поверхности теплообмена F и при этом заданы k, Wx, Wг, конечные температуры и характер относительного движения потоков, то применяют схему расчета с использованием зависимости г = —f(N); в общем виде схема расчета приведена ниже.
По известным конечным температурам вычисляют эффективность , а также отношение Wmin/Wmax. Используя зависимости для заданной схемы движения потоков, по величине Wmin/Wmax определяют N. Площадь поверхности теплообмена
При указанной формулировке задачи использование среднелогарифмической разности температур также не вызывает сложностей и трудоемкость расчета примерно такая же, как и при расчете по методу безразмерных характеристик.


Значения конечных температур теплоносителей определяют из уравнений:
Метод безразмерных характеристик позволяет определить эффективность работы теплообменных аппаратов различных типов. При этом появляется возможность учесть влияние различных факторов на эффективность работы аппарата: схемы движения теплоносителей, числа ходов в перекрестноточных теплообменниках, а также наличия перемешивания теплоносителя (или течения его по отдельным параллельным каналам). Кроме того, этот метод позволяет установить, что перемешивание теплоносителя с меньшей полной теплоемкостью массового расхода приводит к более высокой эффективности работы теплообменника, а также оценить влияние отношения полных теплоемкостей массового расхода теплоносителей на характеристики теплообменника-
http://kskz.ru/stati_sistema_differentsialnyh_uravneniy
http://pandia.ru/text/78/045/84935.php
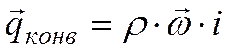
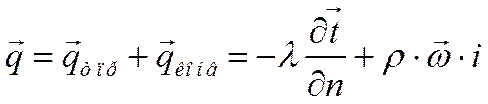
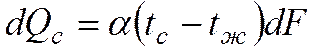
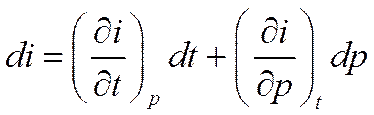
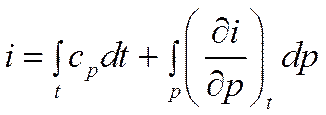
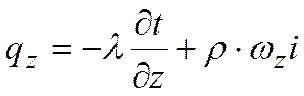
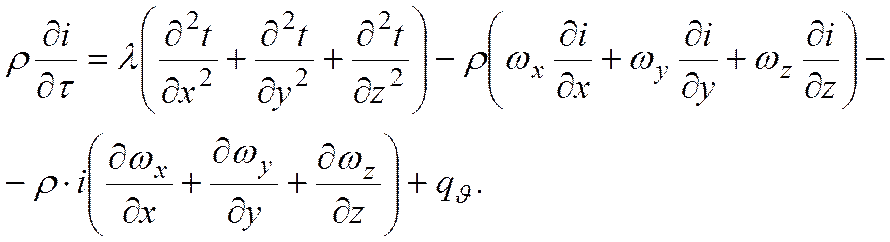
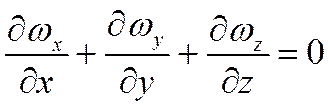
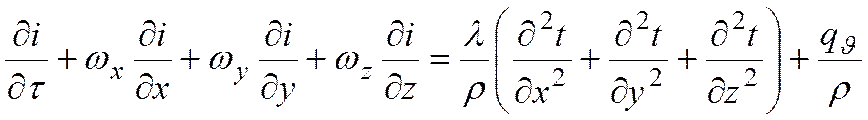
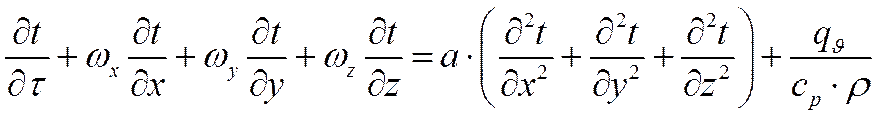
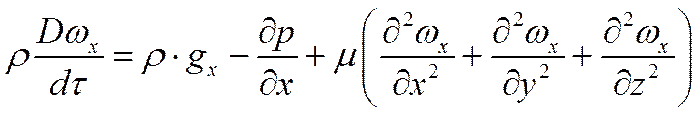
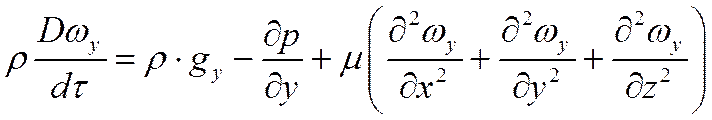
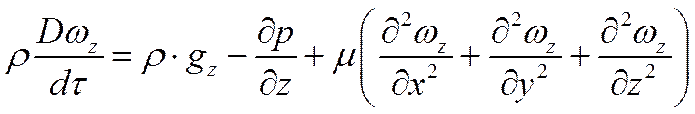
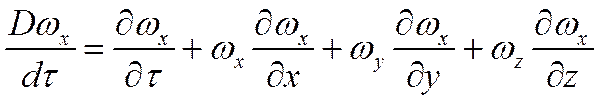
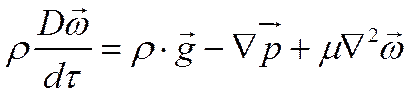
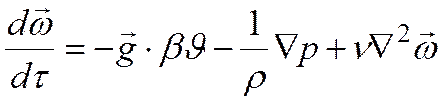
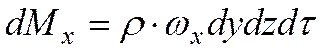
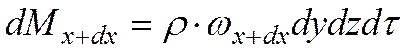
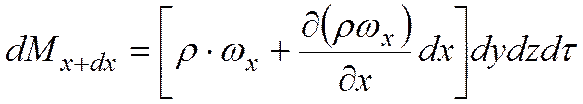
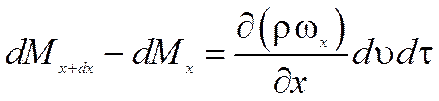
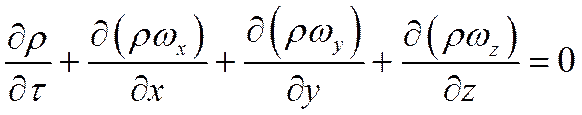
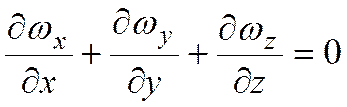

 ,
,  . Точное решение уравнений движения и энергии, составляющих систему нелинейных дифференциальных уравнений в частных производных, возможно лишь в ограниченном числе простейших случаев.
. Точное решение уравнений движения и энергии, составляющих систему нелинейных дифференциальных уравнений в частных производных, возможно лишь в ограниченном числе простейших случаев.
 ГЛАВА 14. ОСНОВЫ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
ГЛАВА 14. ОСНОВЫ КОНВЕКТИВНОГО ТЕПЛООБМЕНА









































