Методы решения уравнений — обзор
В этой статье дан краткий обзор всех основных методов решения уравнений. Здесь также приведены ссылки на материалы с подробной информацией по каждому методу. Это дает возможность познакомиться со всеми методами решения уравнений, а в случае необходимости — изучить методы решения уравнений углубленно.
Метод введения новой переменной (замены переменной)
Метод введения новой переменной, он же метод замены переменной, позволяет решать уравнения f(g(x))=0 или f1(g(x))=f2(g(x)) , где f , f1 и f2 – некоторые функции, а x – неизвестная переменная, а также уравнения, которые могут быть приведены к указанному виду. Состоит метод во введении новой переменной t=g(x) . Введение переменной позволяет от исходного уравнения f(g(x))=0 или f1(g(x))=f2(g(x)) перейти к уравнению с новой переменной f(t)=0 или f1(t)=f2(t) соответственно. Дальше находятся корни полученного уравнения с новой переменной: t1, t2, …, tn . После этого осуществляется возврат к старой переменной, для чего составляется совокупность уравнений g(x)=t1, g(x)=t2, …, g(x)=tn . Решение этой совокупности дает интересующее нас решение исходного уравнения.
Например, метод введения новой переменной позволяет решить уравнение . Здесь стоит принять . Это позволяет перейти от исходного уравнения к квадратному уравнению t 2 −3·t+2=0 с новой переменной t , которое имеет два корня t1=1 и t2=2 . Обратная замена происходит путем составления совокупности двух уравнений и . Это рациональные уравнения. Решением первого является x=2 , а решением второго является x=1,5 . Так методом введения новой переменной получено решение исходного уравнения: 1,5 , 2 .
Подробное описание метода введения новой переменной, включающее обоснование метода, алгоритм решения уравнений этим методом и примеры решения характерных уравнений, дано в этой статье.
Метод разложения на множители
Метод разложения на множители предназначен для решения уравнений f1(x)·f2(x)·…·fn(x)=0 , где f1(x), f2(x),…, fn(x) – некоторые выражения, x – переменная. То есть, методом разложения на множители решаются уравнения, в левой части которых находится произведение нескольких выражений, а в правой – нуль. Суть метода состоит в замене решения уравнения f1(x)·f2(x)·…·fn(x)=0 решением совокупности уравнений f1(x)=0, f2(x)=0, …, fn(x)=0 на области допустимых значений (ОДЗ) для исходного уравнения.
Приведем простой пример. Уравнение может быть решено методом разложения на множители. Переходим от исходного уравнения к совокупности двух уравнений и . Иррациональное уравнение имеет единственное решение x1=1 . Логарифмическое уравнение тоже имеет единственное решение x2=4 . Значит, совокупность уравнений имеет два решения x1=1 , x2=4 . Но области допустимых значений для исходного уравнения, которой является множество (3, +∞) , принадлежит лишь одно из решений x1=1 , x2=4 , а именно, x2=4 . Оно и является единственным корнем уравнения .
Подробное описание этого метода и решения других характерных примеров смотрите в статье «метод разложения на множители».
Метод решения уравнений «дробь равна нулю»
Из названия понятно, что этот метод используется при решении уравнений f(x)/g(x)=0 . Например, он позволяет решить уравнение . Метод состоит в переходе от решения уравнения f(x)/g(x)=0 к решению уравнения f(x)=0 на ОДЗ для исходного уравнения. Следовательно, чтобы решить уравнение , надо решить уравнение (x−1)·(x 2 −4)=0 на ОДЗ для исходного уравнения.
Обоснование метода и примеры с решениями смотрите здесь.
Метод решения уравнений через преобразования
Метод базируется на преобразовании уравнений с целью выстраивания последовательностей равносильных уравнений и уравнений-следствий со сравнительно простыми последними уравнениями, по решениям которых находятся решения исходных уравнений.
Например, для решения уравнения 3·x 4 −48=0 последовательно проводятся два преобразования: переносится слагаемое −48 из левой части уравнения в правую с противоположным знаком, после чего проводится деление обеих частей уравнения на число 3 . В результате получается равносильное уравнение x 4 =16 , причем очень простое в плане решения. Оно имеет два корня x1=−2 и x2=2 . Они и составляют решение исходного уравнения.
Вот другой пример. Замена выражения в левой части уравнения тождественно равным выражением (x−1)·(x+2) дает уравнение-следствие (x−1)·(x+2)=0 , имеющее два корня x1=1 и x2=−2 . Проверка показывает, что только первый корень является корнем исходного уравнения, а второй корень – посторонний.
Какие преобразования используются при решении уравнений? Когда нужно делать проверку для отсеивания посторонних корней, а когда такую проверку делать необязательно? Ответы на эти и многие другие вопросы по теме есть в этом материале.
Метод решения уравнений, сводящихся к числовым равенствам
Иногда в результате преобразования уравнений получаются числовые равенства. Например, уравнение сводится к верному числовому равенству 0=0 , а уравнение сводится к неверному числовому равенству 0=5 . Решением уравнений, сводящихся к верным числовым равенствам, является множество, совпадающее с ОДЗ для исходного уравнения. Так, решением уравнения является множество x≥0 . А уравнения, сводящиеся к неверным числовым равенствам, не имеют решений. То есть, уравнение не имеет решений.
Здесь есть один нюанс. Если среди преобразований, приводящих уравнение к верному числовому равенству, есть возведение обеих частей уравнения в одну и ту же четную степень, то нельзя утверждать, что решением уравнения является любое число из ОДЗ. Этот нюанс разобран в статье «решение уравнений, сводящихся к числовым равенствам».
Функционально-графический метод
Обзор методов решения уравнений продолжаем функционально-графическии методом. Этот метод предполагает использование функций, отвечающих частям решаемого уравнения, а точнее, их графиков и свойств. Можно выделить три основных направления функционально-графического метода:
- Графический метод
- Метод, базирующийся на возрастании-убывании функций
- Метод оценки
Давайте рассмотрим их.
Графический метод
Первое направление базируется на использовании графиков функций. Это так называемый графический метод решения уравнений. По этому методу, во-первых, выполняется построение в одной прямоугольной системе координат графиков функций, отвечающих частям уравнения. Во-вторых, по чертежу определяется количество точек пересечения графиков, сколько точек пересечения – столько и корней у решаемого уравнения. В-третьих, определяются абсциссы точек пересечения – это значения корней.
Например, графически можно решить уравнение . Из чертежа, приведенного ниже, видно, что графики имеют единственную точку пересечения с абсциссой 2 . Это единственный корень уравнения.
Метод, базирующийся на возрастании-убывании функций
Второе направление в своей основе имеет использование свойств возрастающих и убывающих функций. Соответствующий метод используется тогда, когда есть возможность подобрать корень уравнения и доказать возрастание функции, отвечающей одной из частей уравнения, и убывание функции, отвечающей другой части уравнения. В этом случае подобранный корень является единственным.
Приведем пример. Для уравнения 3 (1−x) 3 +1=2 x несложно подобрать корень, им является число 1 . Также несложно обосновать убывание функции, соответствующей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Это доказывает единственность подобранного корня.
За более полной информацией следуйте сюда
Метод оценки
Третье направление основано на использовании свойств ограниченности функций. Это так называемый метод оценки. Согласно этому методу, в первую очередь нужно оценить значения выражений, находящихся в левой и правой части уравнения. Если множества, соответствующие полученным оценкам, не пересекаются, то уравнение не имеет корней. Если множества имеют конечное число общих элементов t1 , t2 , …, tn , то решение уравнения f(x)=g(x) заменяется решением совокупности систем , , …, . Если же множества, соответствующие оценкам имеют бесконечно много общих элементов, то надо либо уточнять оценки, либо искать другой метод решения.
Например, методом оценки можно решить уравнение . Значения левой части этого уравнения не превосходят нуля, а значения правой части не меньше нуля. Это позволяет перейти к системе , решение которой дает искомое решение уравнения.
Метод освобождения от внешней функции
Метод освобождения от внешней функции используется для решения уравнений h(f(x))=h(g(x)) , где f , g и h – функции, причем функция y=h(t) принимает каждое свое значение по одному разу, в частности, строго возрастает или строго убывает, а x – независимая переменная. Этот метод состоит в переходе от уравнения h(f(x))=h(g(x)) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения.
Например, методом освобождения от внешней функции можно решить уравнение . Здесь в качестве внешней функции выступает y=h(t) , где . Эта функция возрастающая как сумма двух возрастающих функций и , значит, каждое свое значение она принимает по одному разу. Это позволяет перейти от исходного уравнения к уравнению . Равносильные преобразования позволяют привести последнее уравнение к квадратному уравнению x 2 +x−2=0 , которое имеет два корня x1=−2 и x2=1 . Из этих корней только x1=−2 принадлежит ОДЗ для исходного уравнения. Следовательно, x1=−2 – единственный корень исходного уравнения.
Рекомендуем детально разобраться с этим методом решения уравнений, обратившись к материалу статьи «метод освобождения от внешней функции».
Метод решения уравнений через ОДЗ
Через ОДЗ решаются уравнения, области допустимых значений которых являются либо пустыми множествами, либо состоят из конечного количества чисел. Когда ОДЗ есть пустое множество, уравнение не имеет решений. Когда ОДЗ состоит из конечного количества чисел, то следует по очереди проверить эти числа через подстановку. Те из них, которые удовлетворяют решаемому уравнению являются его корнями, остальные – не являются.
Например, уравнение не имеет решений, так как ОДЗ для него есть пустое множество. А для уравнения ОДЗ состоит из двух чисел −1 и 7 . Проверка подстановкой показывает, что −1 является корнем уравнения, а 7 – не является.
Более полная информация по этому методу решения уравнений содержится в этой статье.
Метод возведения обеих частей уравнения в одну и ту же степень
Этот метод, в основном, используется для решения иррациональных уравнений. Он заключается в возведении обеих частей уравнения в одну и ту же степень с целью избавления от корней. Например, возведение обеих частей уравнения в квадрат дает уравнение без корня 1−5·x=(x−3) 2 . Возведение в нечетную степень дает равносильное уравнение. Возведение в четную степень в общем случае дает уравнение-следствие, поэтому, при этом необходимо позаботиться об отсеивании посторонних корней. Причем отсеивание следует проводить способом, не связанным с ОДЗ, обычно, через проверку подстановкой, так как возведение частей уравнения в четную степень может приводить к появлению посторонних корней в рамках ОДЗ.
Аналогично разбираемый метод может использоваться и для решения уравнений, в которых фигурируют степени с рациональными и иррациональными показателями. Решения соответствующих примеров смотрите здесь.
Метод решения уравнений по определению логарифма
По определению логарифма, как правило, решают уравнения следующего вида logh(x)f(x)=g(x) , например, log2(x 2 +4·x+3)=3 , log2(9−2 x )=3−x , logx(3·x lgx +4)=2·lgx и т.п.
Согласно методу решения уравнений по определению логарифма, решение уравнения logh(x)f(x)=g(x) заменяется решением уравнения f(x)=(h(x)) g(x) на ОДЗ переменной x для исходного уравнения. Например, от уравнения logx(3·x lgx +4)=2·lgx можно перейти к уравнению 3·x lgx +4=x 2·lgx на ОДЗ для исходного уравнения.
Более полная информация содержится в основной статье.
Метод потенцирования
Методом потенцирования решаются логарифмические уравнения, обе части которых являются логарифмами по одному и тому же основанию, например, lgx=lg(3·x+5) , и т.п. Метод заключается в замене решения уравнения logh(x)f(x)=logh(x)g(x) решением уравнения f(x)=g(x) на ОДЗ для исходного уравнения. По этому методу от уравнения lgx=lg(3·x+5) следует перейти к уравнению x=3·x+5 на ОДЗ для исходного уравнения, которая определяется двумя условиями: x>0 , 3·x+5>0 .
Обоснование метода и примеры с подробными решениями смотрите в этой статье.
Метод логарифмирования
Метод подразумевает логарифмирование обеих частей уравнения по одному и тому же основанию. К нему следует прибегать тогда, когда логарифмирование позволяет избавиться от степеней с переменной в показателях. В частности, его можно использовать для решения показательных уравнений, обе части которых являются степенями с одинаковыми основаниями, например, 5 1−x =5 2·x+1 . Почленное логарифмирование этого уравнения дает очень простое уравнение 1−x=2·x+1 , решение которого дает решение исходного уравнения.
Также метод подходит для решения показательных уравнений, степени в которых имеют разные основания и отличающиеся показатели, например, . Более того, метод логарифмирования является чуть ли не основным методом решения показательно-степенных уравнений, вроде таких x lgx−1 =100 , .
Более детальная информация и примеры с решениями есть в этом материале.
Виды уравнений и методы их решения
В разработке рассматриваются виды алгебраических уравнений и методы их решения.
Просмотр содержимого документа
«Виды уравнений и методы их решения»
Виды уравнений и методы их решения
Уравнения подразделяются на две большие группы: алгебраические и трансцендентные. Алгебраическим называется такое уравнение, в котором для нахождения корня уравнения используются только алгебраические действия, а именно четыре арифметических – сложение, вычитание, умножение и деление, а также возведение в степень и извлечение натурального корня. Трансцендентным называется уравнение, в котором для нахождения корня используются не алгебраические функции: например, тригонометрические, логарифмические и иные.
В курсе математики основной школы рассматриваются только алгебраические уравнения. Рассмотрим более подробно их виды и алгоритм решения.
Группу алгебраических уравнений можно условно разделить на такие виды уравнений как:
целые — с обеими частями, состоящими из целых алгебраических выражений по отношению к неизвестным;
дробные — содержащие целые алгебраические выражения в числителе и знаменателе;
иррациональные — алгебраические выражения здесь находятся под знаком корня.
Дробные и иррациональные уравнения можно свести к решению целых уравнений.
Существует также и ещё одна классификация, которая основывается на степени, которая имеется в левой части многочлена. Исходя из этого различают линейные, квадратные и кубические уравнения. Линейные уравнения также могут называться уравнениями первой степени, квадратные — второй, а кубические, соответственно, третьей.
Рассмотрим особенности решения алгебраических уравнений
В алгебре рассматриваются два вида равенств – тождества и уравнения.
Остановимся на основных понятиях.
Тождество — это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв. Для записи тождества наряду со знаком 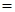
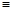
Уравнение — это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют параметрами или коэффициентами уравнения и обычно обозначают первыми буквами латинского алфавита:a, b, c. – или теми же буквами, снабженными индексами: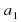
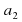
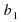
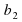
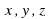
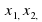
В общем виде уравнение может быть записано так:
F (
В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.
Значение неизвестных, обращающие уравнение в тождество (верное равенство), называют решениями уравнения.
Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.
Если все решения одного уравнения являются решениями другого уравнения, то такие уравнения называют эквивалентными.
Рассмотрим некоторые эквивалентные уравнения:
Уравнение 
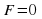
Уравнение 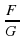
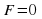
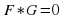
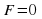
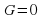
Уравнение 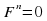
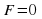
Уравнение 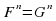
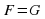
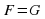
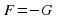
Алгебраическим уравнением называется уравнение вида 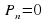
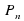
Алгебраическим уравнением с одним неизвестным называется уравнение, сводящееся к уравнению вида:
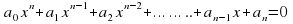
где n – неотрицательное целое число; коэффициенты многочлена называются , ……коэффициентами (или параметрами), называется неизвестным и является искомым. Число n называется степенью уравнения.
Значения неизвестного , обращающие алгебраическое уравнение в тождество, называются корнями (решениями) алгебраического уравнения.
Есть несколько видов уравнений, которые решаются по готовым формулам. Это линейное и квадратное уравнения, а также уравнения вида , где F – одна из стандартных функций (степенная или показательная функция, логарифм, синус, косинус, тангенс или котангенс). Такие уравнения считаются простейшими. Так же существуют формулы и для кубического уравнения, но его к простейшим не относят.
Главная задача при решении любого уравнения – свести его к простейшим.
Все ниже перечисленные уравнения имеют так же и свое графическое решение, которое заключается в том, чтобы представить левую и правую части уравнения как две одинаковые функции от неизвестного. Затем строится график сначала одной функции, а затем другой и точка (и) пересечения двух графиков даст решение (я) исходного уравнения. Примеры графического решения всех уравнений даны в приложении.
Рассмотрим методы решения уравнений.
Линейным уравнением называется уравнение первой степени.
где a и b – некоторые действительные числа.
Линейное уравнение всегда имеет единственный корень , который находится следующим образом.
Прибавляя к обеим частям уравнения (1) число -b, получаем уравнение
, (2) эквивалентное уравнению (1). Разделив обе части уравнения (2) на величину , получаем корень уравнения (1):
Алгебраическое уравнение второй степени (3),
где a, b, с– некоторые действительные числа, называется квадратным уравнением.
Если , то квадратное уравнение (3) называется приведенным.
Корни квадратного уравнения вычисляются по формуле
Выражение называется дискриминантом квадратного уравнения.
если , то уравнение имеет два различных действительных корня;
если , то уравнение имеет один действительный корень кратности 2;
если , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
Частными видами квадратного уравнения (3) являются:
1) Приведенное квадратное уравнение (в случае, если ), которое обычно записывается в виде
Корни приведенного квадратного уравнения вычисляются по формуле
Эту формулу называют формулой Виета – по имени французского математика конца XVI в., внесшего значительный вклад в становление алгебраической символики.
2) Квадратное уравнение с четным вторым коэффициентом, которое обычно записывается в виде
Корни этого квадратного уравнения удобно вычислять по формуле
Формулы (4) и (5) являются частными видами формулы для вычисления корней полного квадратного уравнения.
Корни приведенного квадратного уравнения
связаны с его коэффициентами Формулами Виета
В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
если , , то оба корня отрицательны;
если , , то оба корня положительны;
если , , то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного;
если , , уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
Перепишем еще раз квадратное уравнение
и покажем еще один способ как можно вывести корни квадратного уравнения (6) через его коэффициенты и свободный член. Если
то корни квадратного уравнения вычисляются по формуле
которая может быть получена в результате следующих преобразований исходного уравнения, а так же с учетом формулы (7).
Заметим, что , поэтому
но , из формулы (7) поэтому окончательно
Если положить, что + , то
Заметим, что , поэтому
но , поэтому окончательно
Уравнения n-й степени вида
называется двучленным уравнением. При и заменой (2))
где — арифметическое значение корня, уравнение (8) приводится к уравнению
которое и будет далее рассматриваться.
Двучленное уравнение при нечетном n имеет один действительный корень . В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и комплексных):
Двучленное уравнение при четном n в множестве действительных чисел имеет два корня , а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
Двучленное уравнение при четном n имеет один действительный корней , а в множестве комплексных чисел корней, вычисляемых по формуле
Двучленное уравнение при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет корней, вычисляемых по формуле (10).
Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.
Уравнение имеет два действительных корня .
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение имеет два действительных корния и два комплексных корня .
Уравнение действительных корней не имеет. Комплексные корни: .
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение действительных корней не имеет. Комплексные корни:
Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида
оказались «крепким орешком». В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнем с упрощения
Если кубическое уравнение общего вида
разделить на , то коэффициент при станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:
Чтобы не путаться в коэффициентах, заменим здесь на и перегруппируем слагаемые:
Мы видим, что надлежащим выбором , а именно взяв , можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
Если здесь сделать замену , получим кубическое уравнение относительно без члена с :
Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида
Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:
Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу :
Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений
и взять в качестве сумму и . Заменой , эта система приводится к совсем простому виду:
Дальше можно действовать по-разному, но все «дороги» приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при со знаком минус, а произведение – свободному члену. Отсюда следует, что и — корни уравнения
Выпишем эти корни:
Переменные и равны кубическим корням из и , а искомое решение кубического уравнения (13) – сумма этих корней:
Эта формула известная как формула Кардано.
подстановкой приводится к «неполному» виду
Корни , , «неполного» кубичного уравнения (14) равны
Пусть «неполное» кубичное уравнение (14) действительно.
а) Если («неприводимый» случай), то и
Во всех случаях берется действительное значение кубичного корня.
Алгебраическое уравнение четвертой степени.
где a, b, c – некоторые действительные числа, называется биквадратным уравнением. Заменой уравнение сводится к квадратному уравнению с последующим решением двух двучленных уравнений и ( и — корни соответствующего квадратного уравнения).
Если и , то биквадратное уравнение имеет четыре действительных корня:
Если , (3)), то биквадратное уравнение имеет два действительных корня и мнимых сопряженных корня:
Если и , то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
можно избавиться от члена подстановкой . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
Идея Феррари состояла в том, чтобы представить уравнение в виде , где левая часть – квадрат выражения , а правая часть – квадрат линейного уравнения от , коэффициенты которого зависят от . После этого останется решить два квадратных уравнения: и . Конечно, такое представление возможно только при специальном выборе параметра . Удобно взять в виде , тогда уравнение перепишется так:
Правая часть этого уравнения – квадратный трехчлен от . Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
Это уравнение называется резольвентным (т.е. «разрешающим»). Относительно оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень . При правая часть уравнения (15) принимает вид
а само уравнение сводится к двум квадратным:
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде
и добавим к обеим частям выражение , чтобы в левой части образовался полный квадрат:
Теперь приравняем к нулю дискриминант правой части уравнения:
или, после упрощения,
Один из корней полученного уравнения можно угадать, перебрав делители свободного члена: . После подстановки этого значения получим уравнение
откуда . Корни образовавшихся квадратных уравнений — и . Разумеется, в общем случае могут получиться и комплексные корни.
подстановкой приводится к «неполному» виду
Корни , , , «неполного» уравнения четвертой степени (16) равны одному из выражений
в которых сочетания знаков выбираются так, чтобы удовлетворялось условие
причем , и — корни кубичного уравнения
Уравнения высоких степеней
Разрешимость в радикалах
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения данной степени ( ) можно «обслужить» одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель в начале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля-Руффини звучит так:
Общее уравнение степени при неразрешимо в радикалах.
Таким образом, общей формулы, применимой ко всем уравнениям данной степени , не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой степени – так называемых абелевых уравнений. Теорема Абеля-Руффини не исключает даже и того, что корни каждого конкретного алгебраического уравнения можно записать через его коэффициенты с помощью знаков арифметических операций и радикалов, в частности, что любое алгебраическое число, т.е. корень уравнения вида
с целыми коэффициентами, можно выразить в радикалах через рациональные числа. На самом деле такое выражение существует далеко не всегда. Это следует из теоремы разрешимости алгебраических уравнений, построенной выдающимся французским математиком Эваристом Галуа в его «Мемуаре об условиях разрешимости уравнений в радикалах» (1832 г.; опубликован в 1846 г.).
Подчеркнем, что в прикладных задачах нас интересует только приближенные значения корней уравнения. Поэтому его разрешимость в радикалах здесь обычно роли не играет. Имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам.
Уравнения, которые решаются
Хотят уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнения выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.
В основе одного из таких приемов лежит теорема о рациональных корнях многочлена:
Если несократимая дробь является корнем многочлена с целыми коэффициентами, то ее числитель является делителем свободного члена , а знаменатель — делителем старшего коэффициента .
Для доказательства достаточно подставить в уравнение и умножить уравнение на . Получим
Все слагаемые в левой части, кроме последнего, делятся на , поэтому и делится на , а поскольку и — взаимно простые числа, является делителем . Доказательство для аналогично.
С помощью этой теоремы можно найти все рациональные корни уравнения с целыми коэффициентами испытанием конечного числа «кандидатов». Например, для уравнения
старший коэффициент которого равен 1, «кандидатами» будут делители числа –2. Их всего четыре: 1, -1, 2 и –2. Проверка показывает, что корнем является только одно из этих чисел: .
Если один корень найден, можно понизить степень уравнения. Согласно теореме Безу,
остаток от деления многочлена на двучлен равен , т. е. .
Из теоремы непосредственно следует, что
Если — корень многочлена , то многочлен делится на , т. е. , где — многочлен степени, на 1 меньшей, чем .
Продолжая наш пример, вынесем из многочлена
множитель . Чтобы найти частное , можно выполнить деление «уголком»:
О методах решения линейных систем
Методы решения систем линейных уравнений делятся на две группы – прямые и итерационные. Прямые методы используют конечные соотношения (формулы) для вычисления неизвестных. Они дают решение после выполнения заранее известного числа операций. Эти методы сравнительно просты и наиболее универсальны, т.е. пригодны для решения широкого класса линейных систем.
Вместе с тем прямые методы имеют и ряд недостатков. Как правило, они требуют хранения в оперативной памяти компьютера сразу всей матрицы, и прибольших значениях п расходуется много места в памяти. Далее, прямые методы обычно не учитывают структуру матрицы при большом числе нулевых элементов в разреженных матрицах (например, клеточных или ленточных) эти элементы занимают место в памяти машины, и над ними проводятся арифметические действия. Исключением здесь является метод прогонки (см. разд. 2.2.4). Существенным недостатком прямых методов является также накапливание погрешностей в процессе решения, поскольку вычисления на любом этапе используют результаты предыдущих операций. Это особенно опасно для больших систем, когда резко возрастает общее число операций, а также для плохо обусловленных систем, весьма чувствительных к погрешностям. В связи с этим прямые методы используются обычно для не слишком больших 
Отметим еще, что прямые методы решения линейных систем иногда называют точными, поскольку решение выражается в виде точных формул через коэффициенты системы. Однако точное решение может быть получено лишь при точном выполнении вычислений (и, разумеется, при точных значениях коэффициентов системы). На практике же при использовании компьютеров вычисления проводятся с погрешностями. Поэтому неизбежны погрешности и в окончательных результатах.
Итерационные методы – это методы последовательных приближений. В них необходимо задать некоторое приближенное решение – начальное приближение. После этого с помощью некоторого алгоритма проводят один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводят до получения решения с требуемой точностью. Алгоритмы решения линейных систем с использованием итерационных методов обычно более сложные по сравнению с прямыми методами. Объем вычислений заранее определить трудно.
Тем не менее, итерационные методы в ряде случаев предпочтительнее. Они требуют хранения в памяти машины не всей матрицы системы, а лишь нескольких векторов с п компонентами. Иногда элементы матрицы можно совсем не хранить, а вычислять их по мере необходимости. Погрешности окончательных результатов при использовании итерационных методов не накапливаются, поскольку точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений. Эти достоинства итерационных методов делают их особенно полезными в случае большого числа уравнений, а также плохо обусловленных систем. Следует отметить, что при этом сходимость итераций может быть очень медленной; поэтому ищутся эффективные пути ее ускорения.
Итерационные методы могут использоваться для уточнения решений, полученных с помощью прямых методов. Такие смешанные алгоритмы обычно довольно эффективны, особенно для плохо обусловленных систем. В последнем случае могут также применяться методы регуляризации.
http://multiurok.ru/files/vidy-uravnienii-i-mietody-ikh-rieshieniia.html
http://3ys.ru/metody-resheniya-nelinejnykh-uravnenij-i-zadach-linejnoj-algebry/o-metodakh-resheniya-linejnykh-sistem.html


