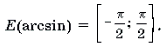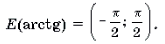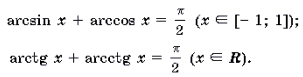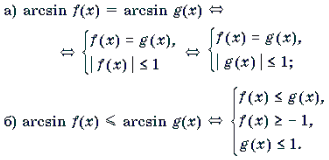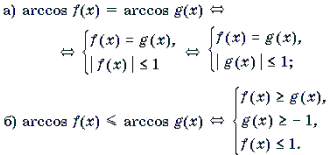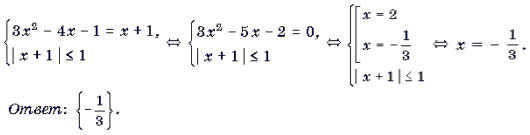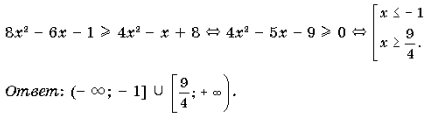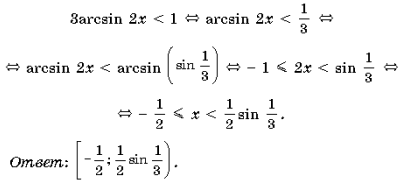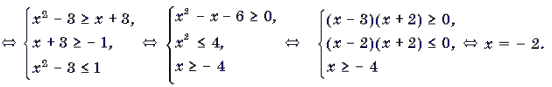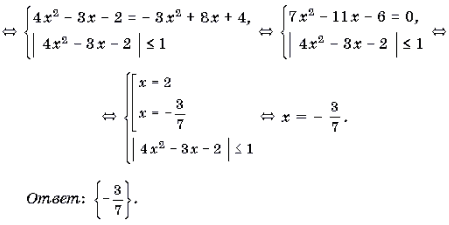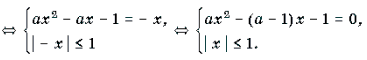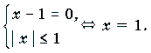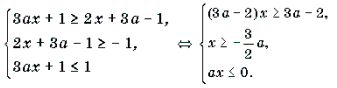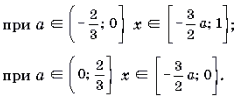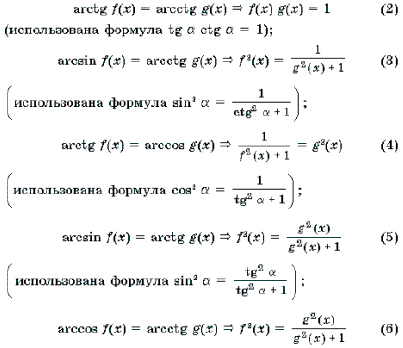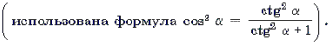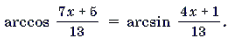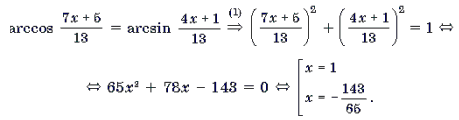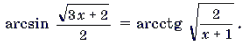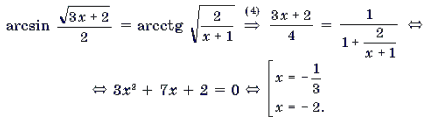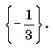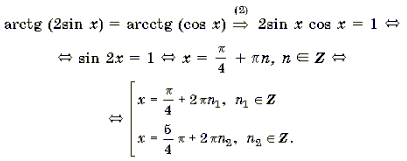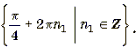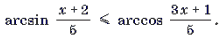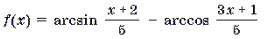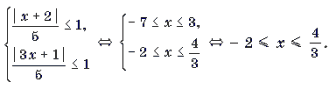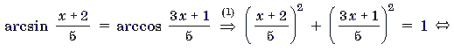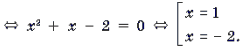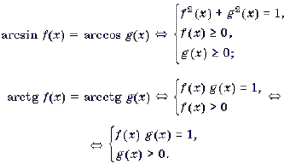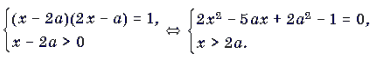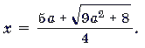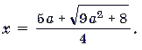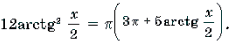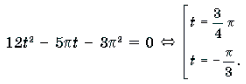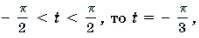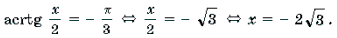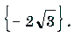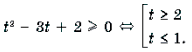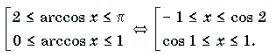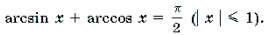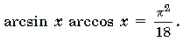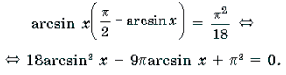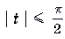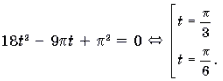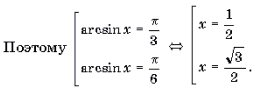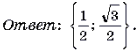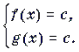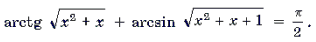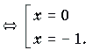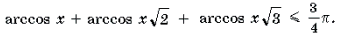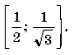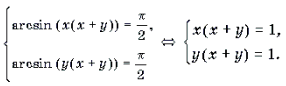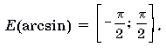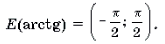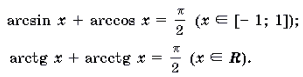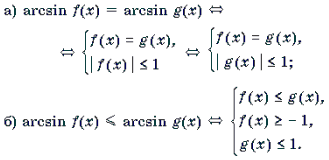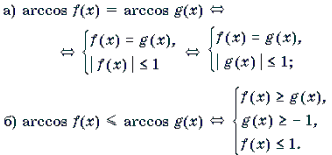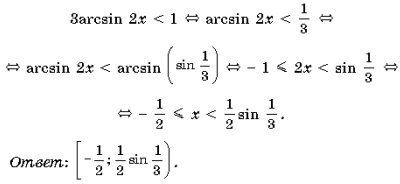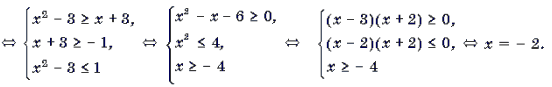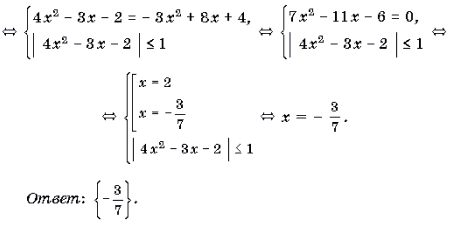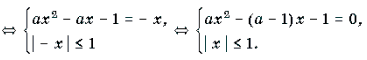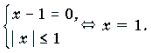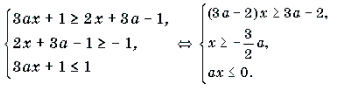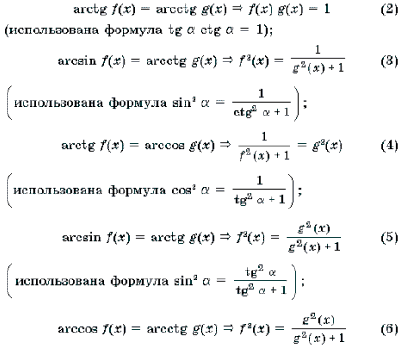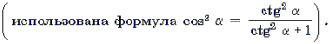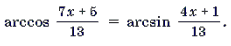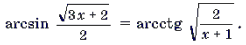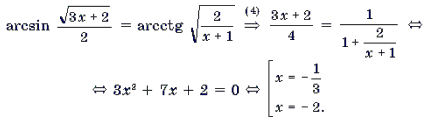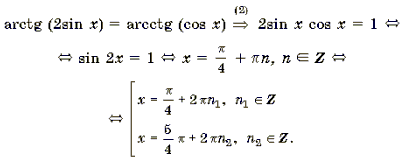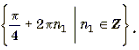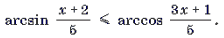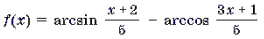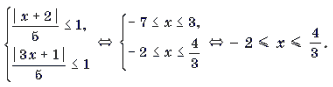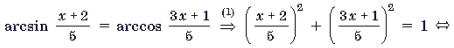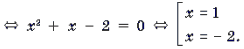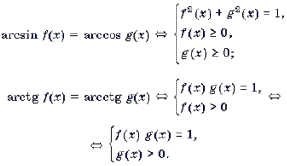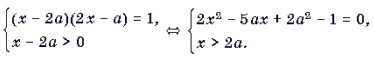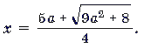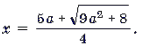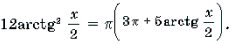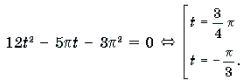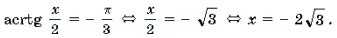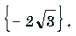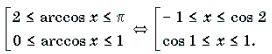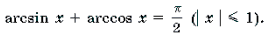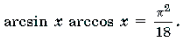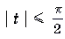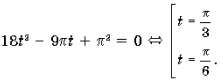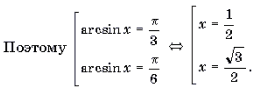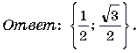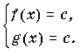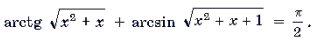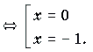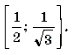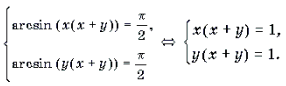Методы решения уравнений содержащих обратные тригонометрические функции

Уравнения и неравенства, содержащие обратные тригонометрические функции

Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода. Предлагаемая вашему вниманию статья посвящена методам решения уравнений и неравенств, содержащих обратные тригонометрические функции. Надеемся, что она окажется полезной для учителей, работающих в старших классах – как общеобразовательных, так и математических.

Вначале напомним важнейшие свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x О [– 1; 1]);

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x О R);

4 Функция y = arcctg x определена и монотонно убывает на R;

Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.

I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями

Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность. Напомним, что функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения. Поэтому справедливы следующие равносильные переходы.

1 .

2 .

3 .

4 .

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

Пример 3. Решить неравенство 3arcsin 2x

Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .

Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:

arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид:

2) a № 0. В этом случае уравнение системы является квадратным. Его корни: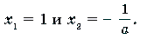
Так как | x | Ј 1, то 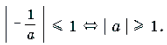. Если a = – 1, то x₂ = x₁ = 1. Если a О (– Ґ Ч ; – 1) И [1; Ґ ), то уравнение имеет два корня.

Ответ: при 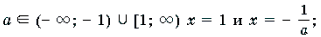при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).

Решение. Неравенство равносильно системе

Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > первое неравенство системы равносильно неравенству x і 1, при a – неравенству x Ј 1, при a = решением первого неравенства является любое действительное число. Множество всех точек (x; a) плоскости Oxa, удовлетворяющих системе, показано на рис. 1 штриховкой.

Ответ: при | a | > решений нет; при a = – x = 1;

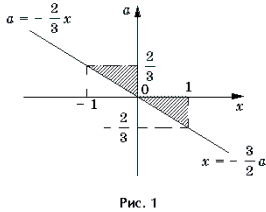
II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями

При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x₀ – решение этого уравнения. Обозначим arcsin f(x₀) = arccos g(x₀) через a. Тогда sin a = f(x₀), cos a = g(x₀), откуда f 2 (x₀) + g 2 (x₀) = 1. Итак, arcsin f(x) = arccos g(x) Ю f 2 (x) + g 2 (x) = 1. (1)

Рассуждая аналогично, можно получить следующие переходы:

Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x₀, для которого f(x₀) і 0 и g(x₀) і 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.

Пример 9. Решить уравнение

Корень 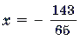является посторонним.

Пример 10. Решить уравнение

Корень x = – 2 является посторонним.

Ответ: .

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Корни вида 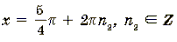являются посторонними.

Ответ:

При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций.

Пример 12. Решить неравенство

Решение. Рассмотрим функцию

и решим неравенство f(x) Ј 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

2) Найдем нули f(x). Для этого решим уравнение

Корень x = – 2 является посторонним.

3) Решим неравенство f(x) Ј 0 методом интервалов.

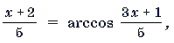
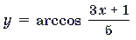
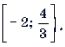
Замечание 4. Заметим, что найдя корень уравнения можно было не обращаться к методу интервалов, а воспользоваться тем, что функция является монотонно возрастающей, а функция монотонно убывающей на отрезке . Поэтому решением исходного неравенства является промежуток [– 2; 1]. Следует, однако, понимать, что метод интервалов является более универсальным, – ведь его можно применять и в тех случаях, когда использование свойств монотонных функций не приводит к искомому результату.

При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе

Графиком квадратного трехчлена f(x) = 2x 2 – 5ax + 2a2 – 1 является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 2a. Это корень

Ответ: при любом a

III. Замена переменной

Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.

Пример 14. Решить уравнение

Решение. Обозначим 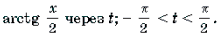После преобразований получим уравнение

Поскольку

откуда

Ответ:

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.

Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда

Поскольку 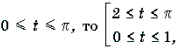откуда

Ответ: [– 1; cos 2] И [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Пример 16. Решить уравнение

Решение. Данное уравнение равносильно следующему:

Пусть arcsin x = t,

Тогда

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.

Теорема 3. Если 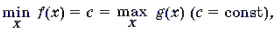то на множестве X уравнение f(x) = g(x) равносильно
системе

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.

Пример 18. Решить уравнение

Решение. Пусть x 2 + x = t. Тогда уравнение примет вид

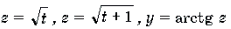
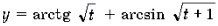
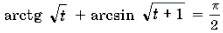
Функции являются монотонно возрастающими. Поэтому функция также является монотонно возрастающей. В силу теоремы 1 уравнение имеет не более одного корня. Очевидно, что t = 0 является корнем этого уравнения. Поэтому x 2 + x = 0

Пример 19. Решить неравенство

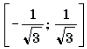
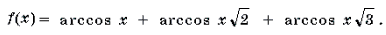
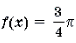
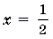
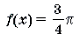
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения. Поэтому решением неравенства является отрезок

Ответ:

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .

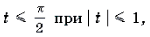
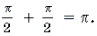
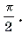
Решение. Поскольку arcsin то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно . Таким образом, уравнение равносильно системе:

Решение последней системы не представляет труда.

Методы решения уравнений содержащих обратные тригонометрические функции

Вначале напомним важнейшие свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x О [– 1; 1]);

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x О R);

4 Функция y = arcctg x определена и монотонно убывает на R;

I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями

1 .

2 .

3 .

4 .

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

Пример 3. Решить неравенство 3arcsin 2x

Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .

Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:

arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид:

Ответ : при при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).

Решение. Неравенство равносильно системе

Ответ: при | a | > решений нет; при a = – x = 1;

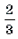
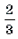
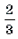
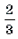
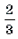
II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями

Рассуждая аналогично, можно получить следующие переходы:

Пример 9. Решить уравнение

Корень является посторонним.

Пример 10. Решить уравнение

Корень x = – 2 является посторонним.

Ответ : .

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Корни вида 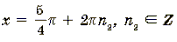являются посторонними.

Ответ :

Пример 12. Решить неравенство

Решение. Рассмотрим функцию

и решим неравенство f(x) Ј 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

2) Найдем нули f(x). Для этого решим уравнение

Корень x = – 2 является посторонним.

3) Решим неравенство f(x) Ј 0 методом интервалов.

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе

Ответ: при любом a

III. Замена переменной

Пример 14. Решить уравнение

Решение. Обозначим 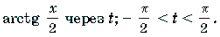После преобразований получим уравнение

Поскольку

откуда

Ответ :

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.

Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда

Поскольку 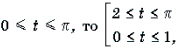откуда

Ответ : [– 1; cos 2] И [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Пример 16. Решить уравнение

Решение. Данное уравнение равносильно следующему:

Пусть arcsin x = t,

Тогда

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.

Теорема 3. Если 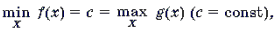то на множестве X уравнение f(x) = g(x) равносильно
системе

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.

Пример 18. Решить уравнение

Решение. Пусть x 2 + x = t. Тогда уравнение примет вид

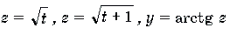
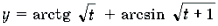
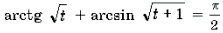
Пример 19. Решить неравенство

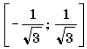
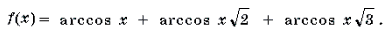
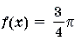
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения. Поэтому решением неравенства является отрезок

Ответ :

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .

Решение. Поскольку arcsin 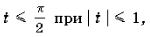то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно . Таким образом, уравнение равносильно системе:

Решение последней системы не представляет труда.

Проектная работа по математике «Методы решения уравнений и неравенств, содержащие обратные тригонометрические функции»

Тригонометрические функции (от греческих слов trigonon – «треугольник» и metreo – «измеряю») – один из важнейших классов функций.

Обратным тригонометрическим функциям в школе обычно уделяется слишком мало времени, и в результате многие учащиеся имеют о них очень смутное представление. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода. Вся теория этих функций кажется туманной и сложной, заполненной к тому же большим количеством головоломных формул, которые невозможно ни вывести, ни запомнить . Предлагаемая вашему вниманию работа посвящена методам решения уравнений и неравенств, содержащих обратные тригонометрические функции. Надеюсь, что она окажется полезной для учеников, которые будут поступать в вузы, и учителей, работающих в старших классах – как общеобразовательных, так и математических.

Составить классификацию методов решений уравнений и неравенств, содержащих аркфункции.

Задачи с аркфункциями в логическом смысле столь же естественны, как и логарифмические функции по отношению к показательным. Однако в школьной программе недостаточно времени уделяется изучению аркфункций. Следует подчеркнуть, что уравнения и графики с аркфункциями столь же разнообразны, как и соответствующие задачи с прямыми тригонометрическими функциями. Они могут быть дополнением к тригонометрии, а также помогут в развитии гибкости математического мышления. Задачи с аркфункциями, т.е. с «непри вычными функциями» позволили нам заглянуть «за страницы» учебника, попробовать начать творческую исследовательскую работу, расширить свой кругозор.

1)Изучить литературу по теме «Тригонометрические функции и тригонометрические уравнения»

2)Составить классификацию методов решения уравнений

3)Применять классификацию методов решения при изучении математики и подготовки к ЕГЭ.

2)От частного к общему

Скачать:

Вложение	Размер
proektnaya_rabota_po_matematike_10_klass.doc	369 КБ

Предварительный просмотр:

Школьная научно- практическая конференция

«Юность — науке и технике»

Тема: « Методы решения уравнений и неравенств, содержащие обратные тригонометрические функции »

Ф.И.О. автора: Ф.И.О. научного

Порозков Александр Иванович, руководителя:

школа 34, 10а класс; Сюткина Надежда

Ежов Николай Николаевич, Михайловна

школа 34, 10а класс. учитель математики

1.1. Основные свойства обратных тригонометрических функций…………….6

1.2. Графики обратных тригонометрических функций………………………. 7

Методы решения уравнений и неравенств, содержащих обратные

2.1. Решение уравнений и неравенств, левая и правая части которых являются одноименными обратными тригонометрическими функциями. ….8

2.2. Решение уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями…………. 13

2.3. Решение методом замены переменной…………………………………….18

2.4. Использование при решении свойств монотонности и ограниченности обратных функций……………………………………………………………. 19

2.5. Решение уравнений и неравенств, используя « прямые» тригонометрические функции от обеих частей…………………………….….23

Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и есть тригонометрические функции, встречаются уже в III в. до н.э. в работах Евклида, Архимеда, Аполлония, Пергского и других. Современную форму теории тригонометрических функций и вообще тригонометрии придал Л. Эйлер. Ему принадлежат определения тригонометрических функции принятая в наши символика.

Составить классификацию методов решений уравнений и неравенств, содержащих аркфункции.

Задачи с аркфункциями в логическом смысле столь же естественны, как и логарифмические функции по отношению к показательным. Однако в школьной программе недостаточно времени уделяется изучению аркфункций. Следует подчеркнуть, что уравнения и графики с аркфункциями столь же разнообразны, как и соответствующие задачи с прямыми тригонометрическими функциями. Они могут быть дополнением к тригонометрии, а также помогут в развитии гибкости математического мышления. Задачи с аркфункциями, т.е. с «непривычными функциями» позволили нам заглянуть «за страницы» учебника, попробовать начать творческую исследовательскую работу, расширить свой кругозор.

1)Изучить литературу по теме «Тригонометрические функции и тригонометрические уравнения»

2)Составить классификацию методов решения уравнений

3)Применять классификацию методов решения при изучении математики и подготовки к ЕГЭ.

2)От частного к общему

Раздел «Тригонометрия», где на основе изучено теоретического материала создавалась классификация методов решения уравнений и неравенств, содержащих аркфункции.

Процесс применения теоретических знаний в практической деятельности на уроках математики и подготовки к ЕГЭ.

В завершении исследовании получены следующие результаты:

1) Приобретение навыков исследовательских работ;

2) Повышение уровня предметной и психологической готовности к ЕГЭ по математике;

3) Побуждение к самостоятельной работе по получению информации и формирование методов и умений самообразования.

1.1. Основные свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x [– 1; 1]);

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

arccos (– x) = – arccos x (x [– 1; 1]);
E(arccos) = [0; ].

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x R);

4 Функция y = arcctg x определена и монотонно убывает на R;

arcctg (– x) = – arcctg x (x R);
E(arcctg) = (0; ).

1.2. Графики обратных тригонометрических функций

y = arcsin x y = arccos x

Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции.

2.1. Решение уравнений и неравенств, левая и правая части которых являются одноименными обратными тригонометрическими функциями.

а) arctg f(x) = arctg g(x) f(x) = g(x);
б) acrtg f(x) ≤ arctg g(x) f(x) ≤ g(x).

а) arcctg f(x) = arcctg g(x) f(x) = g(x);
б) arcctg f(x) ≤ arcctg g(x) f(x) ≥ g(x).

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | ≤ 1 (тогда используем первую систему), или | g(x) | ≤ 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) ≤ arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

Пример 3. Решить неравенство 3arcsin 2x

Пример 4. Решить неравенство arccos (x 2 – 3) ≤ arccos (x + 3).

arccos (x 2 – 3) ≤ arccos (x + 3)

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = .

Решение. Так как – arccos t = arccos (– t), то имеет место следующая цепочка

arccos (4x 2 – 3x – 2) = – arccos (3x 2 – 8x – 4)
arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4)

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a:

arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

arcsin ( ax 2 – ax +1) = – arcsin x
arcsin (ax 2 – ax + 1) = arcsin (– x)

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид:

2) a ≠ 0. В этом случае уравнение системы является квадратным. Его корни:
Так как | x | ≤ 1, то . Если a = – 1, то x 2 = x 1 = 1. Если a (– ∞; – 1) [1; ∞), то уравнение имеет два корня.

Ответ: при при a = – 1 и a = 0,x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) ≤ arccos (2x + 3a – 1).

Решение. Неравенство равносильно системе

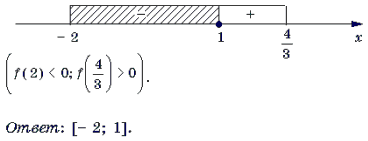
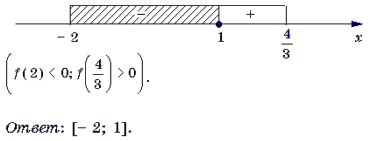
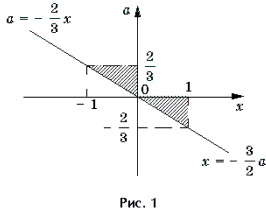
Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > первое неравенство системы равносильно неравенству x ≥ 1, при a – неравенству x ≤ 1, при a = решением первого неравенства является любое действительное число. Множество всех точек (x; a) плоскости Oxa, удовлетворяющих системе, показано на рис. 1 штриховкой.

Ответ: при | a | > решений нет; при a = – x = 1;

2.2. Решение уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями

При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x 0 – решение этого уравнения.

Обозначим arcsin f(x 0 ) = arccos g(x 0 ) через a. Тогда sin a = f(x 0 ), cos a = g(x 0 ), откуда f 2 (x 0 ) + g 2 (x 0 ) = 1. Итак, arcsin f(x) = arccos g(x) f 2 (x) + g 2 (x) = 1. (1)

Рассуждая аналогично, можно получить следующие переходы:

Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x 0 , для которого f(x 0 ) ≥ 0 и g(x 0 ) ≥ 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.

Пример 9. Решить уравнение

Корень является посторонним.

Пример 10. Решить уравнение

Корень x = – 2 является посторонним.

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Корни вида являются посторонними.

Ответ:

Пример 12. Решить неравенство

Решение. Рассмотрим функцию

и решим неравенство f(x) ≤ 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

2) Найдем нули f(x). Для этого решим уравнение

Корень x = – 2 является посторонним.

3) Решим неравенство f(x) ≤ 0 методом интервалов.

Замечание 4. Заметим, что найдя корень уравнения можно было не обращаться к методу интервалов, а воспользоваться тем, что функция является монотонно возрастающей, а функция монотонно убывающей на отрезке . Поэтому решением исходного неравенства является промежуток [– 2; 1]. Следует, однако, понимать, что метод интервалов является более универсальным, – ведь его можно применять и в тех случаях, когда использование свойств монотонных функций не приводит к искомому результату.

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе

Ответ: при любом a

2.3. Решение методом замены переменной.

Пример 14. Решить уравнение

Решение. Обозначим После преобразований получим уравнение

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 ≥ 2.

Решение. Пусть arccos x = t, 0 ≤ t ≤ . Тогда

Ответ: [– 1; cos 2] [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Пример 16. Решить уравнение

Решение. Данное уравнение равносильно следующему:

Пусть arcsin x = t, где

2.4. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 3. Если то на множестве X уравнение f(x) = g(x) равносильно
системе

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Пример 18. Решить уравнение

Решение. Пусть x 2 + x = t. Тогда уравнение примет вид

Пример 19. Решить неравенство

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = .

Решение последней системы не представляет труда.

источники:

http://www.sites.google.com/site/trigonometriavneskoly/obratnye-trigonometriceskie-uravnenia-i-neravenstva

http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2014/09/24/proektnaya-rabota-na-npk-po-matematike-0