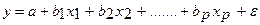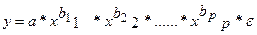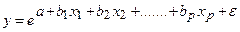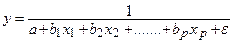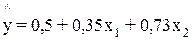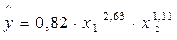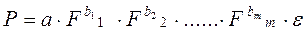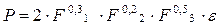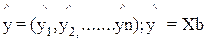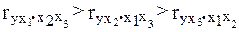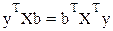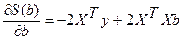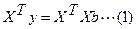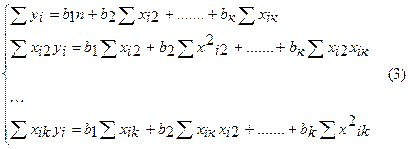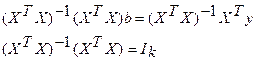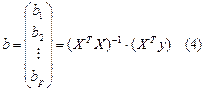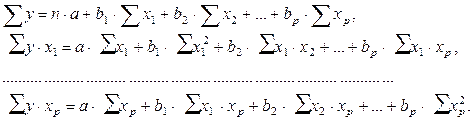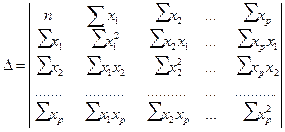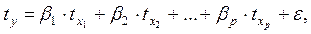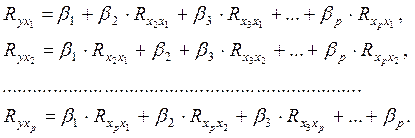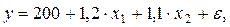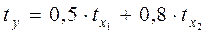Выбор формы уравнения регрессии.
Для построения уравнения множественной регрессии чаще используются следующие функции
1. линейная:
2. степенная:
3. экспоненциальная:
4. гипербола:
В виду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной множественной регрессии параметры при Х называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.
Пример. Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:
где у – расходы семьи за месяц на продукты питания, тыс.руб.;
х1 – месячный доход на одного члена семьи, тыс.руб.;
х2 – размер семьи, человек.
Анализ данного уравнения позволяет сделать выводы – с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35% дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Параметр а не подлежит экономической интерпретации.
При изучении вопросов потребления коэффициенты регрессии рассматривают как характеристики предельной склонности к потреблению. Например, если функции потребления Сt имеет вид:
то потребление в период времени t зависит от дохода того же периода Rt и от дохода предшествующего периода Rt-1. Соответственно коэффициент b0 обычно называют краткосрочной предельной склонностью к потреблению. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на b= b0 + b1. Коэффициент b рассматривается здесь как долгосрочная склонность к потреблению. Так как коэффициенты b0 и b1 >0, то долгосрочная склонность к потреблению должна превосходить краткосрочную b0. Например, за период 1905 – 1951 гг. (за исключением военных лет) М.Фридман построил для США следующую функцию потребления: Сt = 53+0,58 Rt+0,32 Rt-1 с краткосрочной предельной склонностью к потреблению 0,58 и с долгосрочной склонностью к потреблению 0,9.
Функция потребления может рассматриваться также в зависимости от прошлых привычек потребления, т.е. от предыдущего уровня потребления
В этом уравнении параметр b0 также характеризует краткосрочную предельную склонность к потреблению, т.е. влияние на потребление единичного роста доходов того же периода Rt. Долгосрочную предельную склонность к потреблению здесь измеряет выражение b0/(1- b1).
Так, если уравнение регрессии составило:
то краткосрочная склонность к потреблению равна 0,46, а долгосрочная – 0,575 (0,46/0,8).
В степенной функции 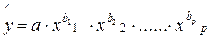
Предположим, что при исследовании спроса на мясо получено уравнение:
где у – количество спрашиваемого мяса
Следовательно, рост цен на 1% при том же доходе вызывает снижение спроса на мясо в среднем на 2.63%. Увеличение дохода на 1% обусловливает при неизменных ценах рост спроса на 1.11%.
В производственных функциях вида:
где P – количество продукта, изготавливаемого с помощью m производственных факторов (F1, F2, ……Fm).
b – параметр, являющийся эластичностью количества продукции по отношению к количеству соответствующих производственных факторов.
Экономический смысл имеют не только коэффициенты b каждого фактора, но и их сумма, т.е. сумма эластичностей: В = b1 +b2+……+bm. Эта величина фиксирует обобщенную характеристику эластичности производства. Производственная функция имеет вид
где Р – выпуск продукции
F1 – стоимость основных производственных фондов
F2 — отработано человеко-дней
F3 – затраты на производство
Эластичность выпуска по отдельным факторам производства составляет в среднем 0,3% с ростом F1 на 1% при неизменном уровне других факторов; 0,2% — с ростом F2 на 1% также при неизменности других факторов производства и 0,5% с ростом F3 на 1% при неизменном уровне факторов F1 и F2. Для данного уравнения В = b1 +b2+b3 = 1. Следовательно, в целом с ростом каждого фактора производства на 1% коэффициент эластичности выпуска продукции составляет 1%, т.е. выпуск продукции увеличивается на 1%, что в микроэкономике соответствует постоянной отдаче на масштаб.
При практических расчетах не всегда 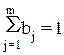
Для уравнения применили равенство:
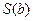
Система нормальных уравнений (1) содержит k линейных уравнений относительно k неизвестных i = 1,2,3……k
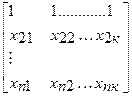
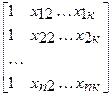
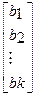
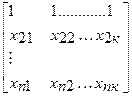
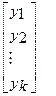
Перемножив (2) получим развернутую форму записи систем нормальных уравнений
Оценка коэффициентов
Стандартизированные коэффициенты регрессии, их интерпретация. Парные и частные коэффициенты корреляции. Множественный коэффициент корреляции. Множественный коэффициент корреляции и множественный коэффициент детерминации. Оценка надежности показателей корреляции.
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.
Так, для уравнения 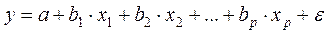
Ее решение может быть осуществлено методом определителей:
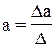
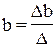
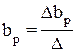
где D – главный определитель системы;
Dа, Db1, …, Dbp – частные определители.
а Dа, Db1, …, Dbp получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Возможен и иной подход в определении параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:
где 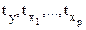
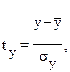
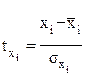
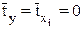
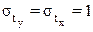
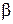
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных вида
Решая ее методом определителей, найдем параметры – стандартизованные коэффициенты регрессии (b-коэффициенты).
Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор хi изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии bI сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.
Пример. Пусть функция издержек производства у (тыс. руб.) характеризуется уравнением вида
где х1 – основные производственные фонды;
х2 – численность занятых в производстве.
Анализируя его, мы видим, что при той же занятости дополнительный рост стоимости основных производственных фондов на 1 тыс. руб. влечет за собой увеличение затрат в среднем на 1,2 тыс. руб., а увеличение численности занятых на одного человека способствует при той же технической оснащенности предприятий росту затрат в среднем на 1,1 тыс. руб. Однако это не означает, что фактор х1 оказывает более сильное влияние на издержки производства по сравнению с фактором х2. Такое сравнение возможно, если обратиться к уравнению регрессии в стандартизованном масштабе. Предположим, оно выглядит так:
Это означает, что с ростом фактора х1 на одну сигму при неизменной численности занятых затрат на продукцию увеличиваются в среднем на 0,5 сигмы. Так как b1
Дата добавления: 2016-05-16 ; просмотров: 2404 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Выбор формы уравнения регрессии
Различают следующие виды уравнений множественной регрессии: линей-ные, нелинейные, сводящиеся к линейным, и нелинейные, не сводящиеся к ли-нейным (внутренне нелинейные). В первых двух случаях для оценки парамет-ров модели применяются классического линейного регрессионного анализа. В случае внутренне нелинейных уравнений для оценки параметров приходится применять методы нелинейной оптимизации.
Основное требование, предъявляемое к уравнениям регрессии, заключает-ся в наличии наглядной экономической интерпретации модели и ее параметров.
Исходя из этих соображений, наиболее часто используются линейная и
| степенная зависимости. | |
| Линейная множественная регрессия имеет вид | |
| yˆ a b1 x1 b2 x2. b p x p. | (3.4) |
Параметры bi при факторах хi называются коэффициентами «чистой» регрессии. Они показывают, на сколько единиц в среднем изменится результативный при-знак y за счет изменения соответствующего фактора на единицу при неизме-ненном значении других факторов, закрепленных на среднем уровне.
Предположим, например, что зависимость спроса на товар (Q d ) от цены (P) и дохода (I) характеризуется следующим уравнением:
Коэффициенты данного уравнения говорят о том, что при увеличении цены на единицу, спрос уменьшится в среднем на 0,12 единиц измерения спроса, а при увеличении дохода на единицу, спрос возрастет в среднем 0,23 единицы.
Параметр а в (3.14) не всегда может быть содержательно проинтерпретирован. Степенная множественная регрессия имеет вид
| yˆ | a x | b | x | b | . x | b p | (3.5) |
| p |
Параметры bj(степени факторов хi) являются коэффициентами эластично-сти. Они показывают, на сколько процентов в среднем изменится результатив-ный признак y за счет изменения соответствующего фактора хi на 1 % при не-измененном значении остальных факторов.
Наиболее широкое применение этот вид уравнения регрессии получил в производственных функциях, а также при исследовании спроса и потребления.
Например, зависимость выпуска продукции Y от затрат капитала K и труда L
говорит о том, что увеличение затрат капитала K на 1 % при неизменных затра-тах труда вызывает увеличение выпуска продукции Y на 0,23 %. Увеличение за-трат труда L на 1 % при неизменных затратах капитала K вызывает увеличение выпуска продукции Y на 0,81 %.
Экономический смысл имеет также сумма коэффициентов bi каждого фак-тора (сумма эластичностей)b = bi. Эта величина дает обобщенную харак-теристику эластичности производства.
Если значение b> 1, то говорят, что функция имеет возрастающий эффект от масштаба производства. Значение b= 1 говорит о постоянном масштабе производства. Если значение b 2 b4 x1 x2 2 ,
величины x1 2 ,x1x2 2 рассматривать как новые дополнительные факторы, то,
| используя замену переменных z | x , z | x | , z | x 2 | , z | x x 2 | , ее можно |
| привести к линейному уравнению регрессии с четырьмя факторами: | |||||||
| y a b1 z1 b2 z2 b3 z3 b4 z4 | . | ||||||
| 3.4. Оценка параметров уравнения линейной | |||||||
| множественной регрессии | |||||||
| Рассмотрим уравнение линейной множественной регрессии | |||||||
| y a b1 x1 b2 x2 | . bpxp . | (3.6) |
Для оценки параметров уравнения множественной регрессии обычно при-меняется метод наименьших квадратов (МНК), согласно которому следует вы-бирать такие значения параметров а и bi, при которых сумма квадратов откло-нений фактических значений результативного признака yi от теоретических значений ŷ= f (x1i,x2i. xpi)(при тех же значениях фактора xij) минимальна, т. е.
С учетом (3.6) величина S является функцией неизвестных параметров а и bi
Оптимальные значения параметров а и bi удовлетворяют условиям
| S | 0, | S | 0, | S | 0, . | S | 0. | (3.8) |
| a | b1 | b2 | bp |
Выполняя соответствующие вычисления, получим для определения пара-метров а и bi следующую систему уравнений
| S | n | |
| 2 ( yia b1x1 | b2 x2 | . bpxp ), |
| a | ||
| i 1 | ||
| S | n | |
| 2b1 ( yia b1x1b2x2 . bpxp ), | ||
| b1 | (3.9) | |
| i 1 | ||
| . | ||
| S | n | |
| 2bp ( yia b1 | x1 b2 | x2. bp x p), |
| bp | ||
| i 1 |
откуда после некоторых преобразований получается система нормальных урав-нений метода наименьших квадратов
| y n a b1 x1 | b 2 x 2 | . bpxp ; | |||||
| yx1 a x1 b1 x1 2 b2 x2 x1 | . bpxpx1 | ; | (3.10) | ||||
| . | |||||||
| yx p a x p | b 1 x 1 x p | b2 x2 x p. bp x2 2 . | |||||
| Решение системы (3.10) удобно записать с помощью матричных обозначе- | |||||||
| ний. Обозначим | 1x11. xp1 | ||||||
| a | y | ||||||
| . x | |||||||
| y | |||||||
| b | , | Y | , | X | 1x | , | (3.11) |
| B 1 | p2 | ||||||
| . | . | ||||||
| . | |||||||
| y | 1x | . x | |||||
| bp | n | ||||||
| 1n | pn |
где B матрица-столбец (p+1×1) из коэффициентов а и bi;
Y матриц-столбец (n×1) исходных значений зависимой переменнойy;
X матрица(p+1×n)исходных значений независимых переменных xi,в ко-торой первый столбец из единиц можно рассматривать как значения «фиктив-
| ной» переменной, соответствующей коэффициенту а. | |
| В этих обозначениях система (3.10) примет вид | |
| (3.12) | |
| (X X )B | X Y , |
| где X‘ транспонированная матрица X. | является неособенной |
| Матрица X X |
квадратной размерности (p+1×p+1) при условии, что столбцы матрицы X ли-нейно независимы.
| Решение системы (3.12) определяется соотношением | |
| (3.13) | |
| B (X X ) | X Y . |
Независимые переменные xi имеют различный экономический смысл, раз-ные единицы измерения и масштаб. Если нужно определить степень относи-тельного влияния отдельных факторов xi на изменение результативной пере-менной y, то переменные xi следует привести к сопоставимому виду. Это мож-но осуществить, вводя, так называемые, «стандартизованные» переменные t y,tx1. txpс помощью соотношений
| t y | y | , | t xi | xi | , (i = 1, 2, …, p) | (3.14) |
| y | x i |
Стандартизованные переменные обладают следующими свойствами: 1) средние значения равны нулю tytxi0; 2) средние квадратические отклоне-
Уравнения множественной регрессии в стандартизованных переменных принимает вид
| t y | 1 | t x | 2 t x | . | p t x | . | (3.15) |
| p |
Величины βi называются стандартизованными коэффициентами. Их связь коэффициентами множественной регрессии bi задается соотношениями
| b | y | или | b | xi | (i = 1, 2, …, p). | (3.16) |
| i | i | |||||
| i | x i | i | y | |||
| Параметр а уравнения (3.6) можно определить из соотношения | ||||||
| a | b2 | . bp | (3.17) |
Стандартизованные коэффициенты регрессии βi показывают, на сколько сигм (средних квадратических отклонений) изменится в среднем результатив-ный признак y за счет изменения соответствующего фактора на одну сигму при неизмененном значении других факторов, закрепленных на среднем уровне.
Система нормальных уравнений МНК (3.10) в стандартизованных пере-менных принимает вид:
| r yx | 1 | 2 rx x | 3rx x | . prx x ; | |||||
| 3 1 | p 1 | ||||||||
| r yx | 1rx x | 2 | 3rx x | . prx x | ; | (3.18) | |||
| p 2 | |||||||||
| . | |||||||||
| r yx | p | 1 r x x | p | 2 rx | x | p | 3 r x x | p | . p . |
Стандартизованные коэффициенты регрессии βi сравнимы между собой, что позволяет ранжировать факторы по силе их воздействия на результат. Большее относительное влияние на изменение результативной переменной y оказывает тот фактор, которому соответствует большее по модулю значение коэффициента βi.
Отметим, что в случае парной линейной регрессии стандартизованный ко-эффициент регрессии β совпадает с линейным коэффициентом корреляции ryx.
Для оценки параметров нелинейных уравнений множественной регрессии предварительно осуществляется преобразование последних в линейную форму (с помощью замены переменных) и МНК применяется для нахождения пара-метров линейного уравнения множественной регрессии в преобразованных пе-ременных.
В случае внутренне нелинейных зависимостей (которые невозможно при-вести к линейному виду) для оценки параметров по методу наименьших квад-ратов приходится применять методы нелинейной оптимизации (п. 2.4).
http://megaobuchalka.ru/5/7167.html