Миллион за уравнение навье стокса

Математики нашли проблему в знаменитых уравнениях для описания жидкостей

Два математика доказали, что при определённых экстремальных условиях уравнения Навье-Стокса выдают бессмыслицу

Уравнения Навье-Стокса при помощи нескольких лаконичных членов описывают одно из самых распространённых явлений физического мира: течение жидкостей. Сегодня эти уравнения, появившиеся ещё в 1820-х, используются для описания всего, от океанских течений и турбулентности, следующей за самолётом до потока крови в сердце.

Хотя физики считают эти уравнения надёжными, как молоток, математики относятся к ним с недоверием. Для математика то, что эти уравнения вроде бы работают, мало что значит. Им нужны доказательства того, что уравнения безошибочны: что для любой жидкости и для долгосрочного прогноза, распространённого сколь угодно далеко в будущее, математика уравнений не подведёт. Такую гарантию оказалось нелегко отыскать. Первый человек или команда, которая сумеет доказать, что уравнения Навье-Стокса будут работать всегда — или представить пример, доказывающий, что они не работают — сможет получить награду за решение одной из «Задач тысячелетия», анонсированных математическим институтом Клэя, и миллионом долларов в придачу [по состоянию на 2017 год только одна из семи задач тысячелетия (гипотеза Пуанкаре) решена Григорием Перельманом / прим. перев.].

Математики разработали множество способов для решения этой задачи. Новая работа, опубликованная в сентябре, ставит серьёзные вопросы по поводу того, сможет ли добиться успеха один из самых популярных подходов к задаче, разрабатываемый в течение многих лет. Работа, которую написали Тристан Бакмастер и Влад Викол из Принстонского университета, представляет собой первый результат, показывающий, как при определённых условиях уравнения Навье-Стокса дают противоречивое описание физического мира.

«Мы пытаемся понять определённые проблемы, присущие этим уравнениям, и то, почему людям, вероятно, придётся их переосмыслить», — говорит Бакмастер.

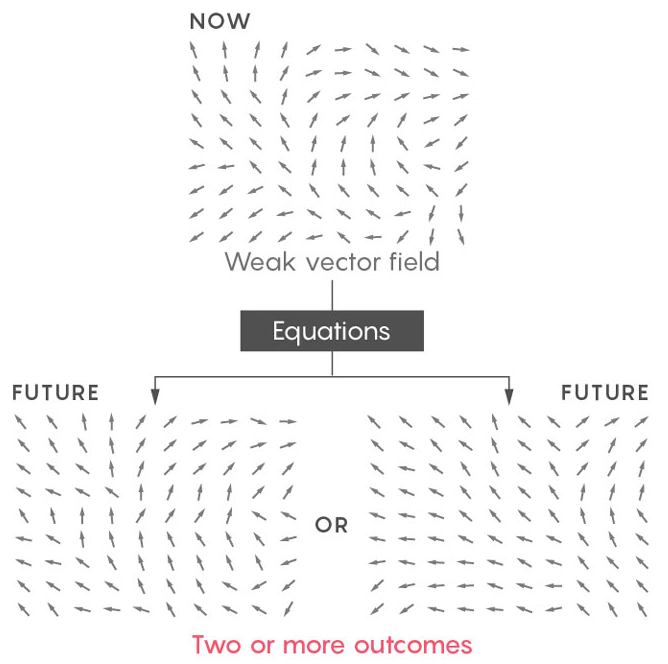
Работа Бакмастера и Викола показывает, что, если принять при решении уравнений Навье-Стокса очень грубые допущения, они начинают выдавать бессмыслицу: утверждают, что одна и та же жидкость с одними и теми же начальными условиями может прийти в два или более различных состояний. Она может течь одним образом, или же совершенно другим. Если так, то эти уравнения не могут надёжно описывать физический мир, для которого они были разработаны.

Взрывая уравнения

Чтобы понять, как уравнения могут сломаться, представьте себе океанское течение. В его рамках могут существовать локальные течения, в результате чего некоторые его части могут перемещаться в одном направлении и с одной скоростью, а другие — в другом направлении с другой скоростью. Локальные течения взаимодействуют друг с другом в постоянном взаимном действии трения и давления воды, определяющих её поток.

Математики моделируют это взаимодействие при помощи карты, сообщающей вам о направлениях и скорости потока в любой точке жидкости. Эта карта, называемая векторным полем — снимок внутренней динамики жидкости. Уравнения Навье-Стокса берут этот снимок и воспроизводят его, как видео, сообщая, как именно будет выглядеть векторное поле в каждый последующий момент времени.

Карта ветров (windy.com) работает похожим на векторное поле образом. В каждой точке у ветра есть определённое направление и сила

Эти уравнения работают. Они описывают течение жидкости так же надёжно, как уравнения Ньютона предсказывают будущие положения планет; физики постоянно используют их, и они постоянно совпадают с результатами экспериментов. Однако математикам нужно нечто большее, чем эпизодическое подтверждение — им нужно доказательство того, что уравнения не нарушаются, что вне зависимости от того, с какого векторного поля вы начнёте, и от того, как далеко в будущее вы будете его воспроизводить, уравнения всегда дадут вам новое, уникальное векторное поле.

Это и есть тема Задачи тысячелетия, спрашивающей, есть ли у уравнений Навье-Стокса решения (решение, по сути, и есть векторное поле) для всех начальных точек во все моменты времени. Эти решения должны обеспечить точное направление и силу потока в каждой точке жидкости. Решения, дающие информацию с таким бесконечно мелким разрешением, называются «гладкими». У гладкого решения каждая точка поля имеет связанный с ней вектор, позволяющий вам «гладко» путешествовать по полю, не застревая в точках, где вектор отсутствует — в точке, дальнейшее движение из которой вам будет непонятно.

Гладкие решения — полное представление физического мира, но с математической точки зрения они могут существовать не всегда. Математики, работающие над уравнениями, подобными этим, переживают по поводу такой ситуации: вы запускаете уравнения Навье-Стокса и наблюдаете за изменениями векторного поля. По прошествии какого-то конечного времени уравнения говорят вам, что некая частица жидкости двигается с бесконечной скоростью. Тогда у вас будут проблемы. В уравнения входит измерение изменений таких свойств, как давление, трение, скорость жидкости — говоря жаргонным языком, они берут производные этих величин — но производную от бесконечной величины взять не проще, чем поделить на ноль. Так что если уравнения выдают бесконечное значение, можно сказать, что они отказали вам, или «взорвались». Они уже не могут описывать последующие состояния вашей жидкости.

Такой «взрыв» — свидетельство того, что в уравнениях не хватает описания каких-то свойств физического мира, который они должны описывать. «Возможно, уравнения охватывают не все эффекты реальной жидкости, поскольку в реальной жидкости мы не ожидаем» бесконечной скорости движения частиц, как говорит Бакмастер.

Решение Задачи тысячелетия состоит либо в том, чтобы показать, что уравнения Навье-Стокса никогда не взрываются, либо найти условия, при которых это происходит. Одна из стратегий, используемых математиками — смягчить требования к тому, как точно эти уравнения должны описывать требуемые решения.

Нарушение потока

Уравнения Навье-Стокса должны описывать течение любой жидкости, с любыми начальными условиями, и распространять описание бесконечно далеко в будущее. Пытаясь доказать эту их способность, математики иногда «ослабляют», то есть, используют приближённые описания векторных полей, описывающих жидкость. Но с этим возникают трудности.

В идеале, математики хотят доказать, что применение уравнений Навье-Стокса к любой непрерывной, «гладкой» жидкости выдаст один уникальный результат.

Однако проще работать со «слабыми», не такими детализированными векторными полями. И вот математики обнаружили, что некоторые слабые описания выдают неуникальные результаты — позволяют одной и той же жидкости в одних и тех же начальных условиях течь двумя способами.

От слабых к гладким

Когда математики изучают такие уравнения, как эти, они иногда начинают расширять определение того, что считается решением. Гладким решениям требуется максимум информации — в случае с Навье-Стоксом им требуется, чтобы в каждой точке векторного поля, связанного с жидкостью, существовал вектор. Но что, если ослабить требования, и сказать, что вам нужно подсчитывать вектора только для некоторых точек поля, или нужно получить только примерные значения векторов? Такие решения называют «слабыми». Они позволяют математикам почувствовать поведение уравнения без утомительной работы по поиску абсолютно всех решений (что на практике может оказаться и невозможным).

Тристан Бакмастер, математик из Принстонского университета

«С какой-то точки зрения слабые решения ещё легче описать, чем реальные, поскольку знать нужно гораздо меньше», — сказал Камилло Де Леллис, в соавторстве с Лазло Щекелихиди написавший несколько важных работ, заложивших фундамент для работы Бакмастера и Викола.

Слабые решения бывают разной градации. Если представить себе гладкое решение в виде математического изображения жидкости с бесконечным разрешением, то слабые решения будут представлять собой нечто вроде 32-битных, 16-битных или 8-битных версий этого изображения.

В 1934 году французский математик Жан Лере определил важный класс слабых решений. Вместо работы с точными векторами, «решения Лере» берут среднее значение векторов в небольшой окрестности векторного поля. Лере доказал, что всегда можно решить уравнения Навье-Стокса, позволяя вашим решениям принимать форму такого вида. Иначе говоря, решения Лере не взрываются.

Достижение Лере определило новый подход к задаче Навье-Стокса: начать с решений Лере, о существовании которых уже известно, и посмотреть, можно ли превратить их в гладкие решения, существование которых вы хотите доказать. Этот процесс напоминает тот, где вы начинаете с грубой картинки, и смотрите, нельзя ли постепенно подкрутить разрешение, чтобы достичь идеального изображения реальности.

«Одна из возможных стратегий — показать, что эти слабые решения Лере гладкие, и если вы сможете показать, что они гладкие — вы решите Задачу тысячелетия», — сказал Бакмастер.

Влад Вкол представляет собой половину команды, вскрывшей проблемы в подходе к проверке уравнений Навье-Стокса.

Есть и ещё один подвох. Решения уравнений Навье-Стокса соответствуют реальным физическим событиям, а физические события происходят одним возможным образом. Учитывая это, хотелось бы, чтобы у ваших уравнений был только один набор уникальных решений. Если уравнения дают вам множество возможных решений, они не справляются со своей задачей.

Поэтому математики смогут использовать решения Лере для решения Задачи тысячелетия, только если решения Лере уникальны. Неуникальные решения Лере будут означать, что, согласно правилам Навье-Стокса, одна и та же жидкость с одними и теми же начальными условиями может прийти к двум разным физическим состояниям, что не имеет физического смысла, и подразумевает, что уравнения на самом деле не описывают то, что должны.

Новый результат Бакмастера и Викола — первый намёк на то, что для определённых определений слабых решений может происходить именно это.

Множество миров

В своей новой работе Бакмастер и Викол рассматривают ещё более слабые решения, чем решения Лере — решения, в которых используется тот же принцип усреднения, что у и Лере, но ослаблено ещё одно дополнительное требование (известное, как неравенство энергий). Они используют метод «выпуклого интегрирования», берущий начало из работ по геометрии математика Джона Нэша, и позднее привлечённый к изучению жидкостей Де Леллисом и Щекелихиди.

Используя такой подход, Бакмастер и Викол доказывают, что эти очень слабые решения уравнений Навье-Стокса неуникальны. Они, к примеру, демонстрируют, что если начать с полностью спокойной жидкости, к примеру, со стакана с водой рядом с кроватью, возможны два вида развития событий. Первый очевиден: вода начинает со спокойного состояния и остаётся спокойной всегда. Второй фантастичный, но математически возможный: вода начинает со спокойного состояния, взрывается в середине ночи, а затем возвращается в спокойное состояние.

«Это доказывает отсутствие уникальности, поскольку из начальных данных можно сконструировать по меньшей мере два объекта», — говорит Викол.

Бакмастер и Викол доказали существование множества неуникальных слабых решений (не только тех двух, что описаны выше) уравнений Навье-Стокса. Важность этого доказательства ещё предстоит понять. В какой-то момент слабые решения могут стать настолько слабыми, что они перестанут быть связанными с более гладкими решениями, которые должны имитировать. Если так и есть, тогда результат, полученный Бакмастером и Виколом, мало к чему приведёт.

«Такой результат однозначно является предупреждением, но можно спорить о том, что это предупреждение касается самой слабой идеи слабых решений. Существует множество слоёв более сильных решений, на гораздо лучшее поведение которых можно возлагать надежду» в случае уравнений Навье-Стокса, — говорит Де Леллис.

Бакмастер и Викол также мыслят в терминах слоёв, и он нацелились на решения Лере — на доказательство того, что и те допускают множественную физику, в которой одна и та же жидкость из одного и того же состояния может прийти к разным формам в будущем.

«Мы с Тристаном считаем, что решения Лере неуникальны. Мы пока этого не доказали, но наша работа закладывает плацдарм для атаки на эту задачу», — сказал Викол.

Чтобы заработать миллион долларов, достаточно решить эти задачи

Математическим институтом Клэя было предложено несколько интересных вопросов, за ответ на каждый из них предусмотрена денежная премия. Чтобы заработать миллион долларов, достаточно решить эти задачи. Испытать свои силы может каждый. Пока удалось справиться лишь с одним. В 2006 году Григорий Перельман был награждён Филдсофской премией (гипотеза Пуанкаре). Примечательно, что от материального вознаграждения учёный отказался.

Проблема перебора

К классу P относят задачи, которые компьютер способен решить очень быстро. Те, правильность результата которых можно проверить, относят к NP.

Допустим, есть 5 монеток номиналом 2, 3, 5, 6 и 7. Необходимо заплатить всего 21 рубль. Возможно ли набрать требуемую сумму из имеющихся монет? Чтобы доказать, что решить задачу нельзя, понадобится перебрать все варианты, а для получения ответа — рассмотреть несколько из них. При увеличении числа монеток на несколько порядков решение окажется непрактичным. Одновременно с этим, для проверки результата необходимо лишь сложить номиналы.

Чтобы решить эту задачу, потребуется ответить на следующий вопрос: равны ли классы P и NP. Удостовериться, что решение верно, или опровергнуть правильность полученного результата несложно, однако специалисты утверждают, что всё не так легко. Если вдруг окажется, что рассматриваемые классы равны, в криптографии произойдёт настоящий переворот.

Можно привести ещё один пример. Известно, что на дне моря находится клад, однако нет сведений о том, где именно он расположен. Так, поиски сокровищ могут длиться сколько угодно. Если известно, что объект находится в определённом квадрате, есть конкретные координаты, его удастся отыскать гораздо быстрее.

Чтобы получить миллион долларов, необходимо найти хотя бы одну задачу, на решение которой ушло бы меньше времени, чем на проверку верности полученного результата.

Гипотезы Ходжа и Римана

Вильям Ходж выдвинул предположение о том, что каждое геометрическое тело может быть исследовано по типу алгебраического уравнения и можно сформировать математическую модель любого подобного объекта. Удобнее всего анализировать составляющие по отдельности, но тут появляется одна проблема. Ведь исследование одного взятого камня не позволяет сделать выводы о крепости, созданной из подобных объектов. Невозможно узнать, как много в ней комнат и какими очертаниями обладает каждое из помещений.

Помимо этого, при формировании первоначального объекта из составных частей могут появиться лишние компоненты. Можно также и недосчитаться некоторых составляющих. Условия, при которых не будут появляться «лишние» части, но одновременно с этим ни один компонент не потеряется, были описаны Ходжем. Он вывел соответствующую формулу. Так, уже 70 лет никто из учёных не может ни доказать, ни опровергнуть это предположение.

Гипотеза указывает на глубокую связь между:

Если удастся её доказать, то такие инструменты, как уравнение Лапласа и топологические варианты, позволят ответить на многие вопросы.

Наверное, каждый помнит из школьной программы, что существуют числа, которые можно разделить только на единицу или на самих себя, они называются простыми. Наибольшее из них включает 12978189 цифр. Число удалось найти ещё в 2008 году. Для математиков подобные значения крайне важны, однако до сих пор непонятно, каким образом происходит их распределение по числовому ряду.

Бернхард Риман выявил метод, позволяющий находить простые числа, не превышающие определённое заданное значение. Пока проверка этого способа проходит успешно (найдено уже полтора триллиона числовых решений), однако нет уверенности, что так будет продолжаться и дальше. Тот, у кого получится доказать его дальнейшую успешность, получит огромное денежное вознаграждение.

Уравнения Навье-Стокса

Подобные уравнения выступают базой для проведения расчётов в геофизической гидродинамике. Каждое движение сопровождают те или иные изменения в среде. Допустим, когда плывёт лодка, это заставляет волны расходиться, а после летящего самолёта появляются турбулентные потоки. Рассматриваемые уравнения как раз и описывают подобные процессы. Однако до сих пор никто не смог их решить.

Не исключено, что сделать это попросту невозможно. Учёные из различных сфер с успехом используют уравнения, задействуя известные значения:

Если кто-то сумеет применить уравнения в обратном направлении или доказать, что решить их невозможно, этот человек получит огромную сумму.

Теория Янга-Миллса

Физикам удалось отыскать метод объединения теорий слабого и мощного электромагнитного воздействия. На основе этих гипотез было спрогнозировано открытие новых частиц, однако не получилось определить их правильную массу. До сих пор остаётся неясным, как именно работают уравнения учёных и действительно ли они верны.

Таким образом, в жизни человека, так или иначе, всё связано с математикой. Бесспорно, это царица наук. Исследователи уже много лет бьются над объяснением некоторых гипотез. Тот, кто сможет решить хотя бы одну из этих непростых задач, получит огромное денежное вознаграждение суммой 1 миллион долларов.

Так, любой из тех, кому нравится жить в мире цифр и формул, может оказаться счастливым миллионером.

Гидродинамика Шрёдингера на пальцах

В этой статье в качестве эксперимента я постараюсь максимально доступно рассказать, как работает новый метод расчёта гидродинамики, основанный на решении уравнения Шрёдингера.

Всем привет. В этой статье я хотел бы рассказать о новом методе расчёта гидродинамики, основанном на решении уравнения Шрёдингера вместо уравнений, типично используемых для гидродинамики вроде Навье-Стокса. Сам метод очень подробно и полно раскрыт в диссертации Albert Chern’а, названной «Fluid Dynamics with Incompressible Schrödinger Flow». Однако, статья Chern’а кому-то может показаться написанной на не самом доступном языке, поэтому своей статьёй я бы хотел в первую очередь если не объяснить в деталях, как работает этот метод, то хотя бы объяснить, какими интересными свойствами он обладает, и что же именно скрывается за его математикой. Попутно я кратко расскажу о том, как устроены классические методы расчёта гидродинаимики и как новый подход от них отличается. В качестве эксперимента я бы хотел попробовать написать статью так, чтобы каждый, кто отдалённо интересуется программированием физики, нашёл в ней что-то интересное, понятное, и новое для себя — от начинающего программиста до бывалых расчётчиков.

Вступление

Почему это важно? В первую очередь потому, что это обозначает глубинное родство квантовомеханических и гидродинамических систем. В диссертации того паренька больше сотни страниц уделено тому, как это вообще так получилось. С участием явления сверхтекучести, которая является загадочным связующим звеном, так как проявляет очевидные свойства идеальной жидкости, являющиеся исключительно следствием квантовой механики. Я же в этой статье далее я рассмотрю только некоторые из параллелей, которые из этого, простите, вытекают.

Следующее очень важное следствие эквивалентности уравнения Шрёдингера и Навье-Стокса — это что решение одного из них эквивалентно решению другого. Так вот уравнение Навье-Стокса — нелиненое, его очень неудобно и неэффективно в общем случае решать, в то время как уравнение Шрёдингера — линеное и его решать гораздо проще. Чтобы составить представление, насколько же неудобным по сей день считается уравнение Навье-Стокса, могу сообщить, что существует целый международный фонд грантов для исследователей, которым хоть какую-то базу под них подстроит, так как(цитата):

Even basic properties of the solutions to Navier–Stokes have never been proven.

Уравнение Шрёдингера же, хоть и описывает мутную квантовую физику, поддаётся решению гораздо легче и эффективнее. Короче, я могу очень долго гудеть про то, как это невероятно и офигенно, но давайте уже перейдём к чему-то более конкретному.

Решение классической гидродинамики на пальцах

Что вообще такое — уравнение гидродинамики? Что такое уравнение Навье-Стокса и как его понять? С ответом на этот вопрос гораздо лучше меня справились миллионы авторов статей по этому делу, например, классическая статья от нвидии, по которой многие начинали: https://developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html Однако, я попробую написать очень сжато и на пальцах, что это всё значит и что с этим обычно делают.
Уравнение Навье-Стокса описывает закон, которому обязана подчиняться скорость каждой точки пространства, заполненного равномерной несжимаемой жидкостью. Представьте себе, например, бассейн с водой, в котором выделили некоторый куб, достаточно далеко от стенок, поверхности и дна, в котором нет ничего кроме воды. Вода в нём может как угодно течь, но не может ни образовывать пузырей, ни с чем-то сталкиваться (мы для простоты опустим эти эффекты). Тогда само уравнение Навье-Стокса описывает закон, которому будет подчиняться скорость каждой точки воды в этом кубе:

\(\frac<\partial \vec u><\partial t>=-(\vec u \cdot \vec \nabla)\vec u-\frac<1><\rho>\vec \nabla p + \nu <\vec \nabla>^2 \vec u + \vec F\)
\(\vec \nabla \vec u = 0\)

прежде чем вообще смотреть на это уравнение, предлагаю сразу из него выбросить ненужное — то, что нам всё равно не пригодится для понимания и только место занимает. Это член, отвечающий за диффузию \(\nu <\vec \nabla>^2 \vec u\) (у идеальной жидкости один фиг диффузии нет), и за внешнюю силу \(\vec F\) (так как мы обойдёмся без неё). Остаётся система:
\(\frac<\partial \vec u><\partial t>=-(\vec u \cdot \vec \nabla)\vec u-\frac<1><\rho>\vec \nabla p\)
\(\vec \nabla \vec u = 0\)
Здесь перевёрнутый треугольник называется оператором Набла, который обозначает дифференцирование. Причём смысл этого оператора меняется в зависимости от того, где именно он стоит (например, перед вектором или скаляром). Я постараюсь объяснить смысл каждого его вхождения по порядку. На пальцах смысл всей формулы в следующем. \(\vec u(\vec x)\) — это значение скорости жидкости, которое определяется в каждой точке пространства \(\vec x\) . Уравнение описывает закономерности, которым обязана подчиняться эта величина, если она описывает поведение несжимаемой жидкости. Работает хоть для двумерного, хоть для трёхмерного случая. В левой части первого уравнения стоит \(\frac<\partial \vec u(\vec x)><\partial t>\) — это величина называется производной по времени и показывает, как быстро и куда(это вектор) изменится скорость в точке \(\vec x\) в момент времени \(t\) .

Нулевой вектор производной по времени обозначает, что скорость в этой точке сейчас не меняется, а, например, вектор (10, 0)[м/c 2 ] обозначает, что за следующую секунду скорость вырастет на 10[м/с] по оси x(если сама производная не поменяется).

Слагаемое вида \(-(\vec v \cdot \vec \nabla)\vec u\) называется адвекцией и говорит, что поле скоростей \(\vec u\) в этой точке утекает в направлении \(\vec v\) . В нашем же случае \(\vec u = \vec v\) , то есть поле скоростей сносит само себя. Это, кстати, и называется нелинейностью и из-за этого возникает миллион проблем при решении этого уравнения.

В принципе, смысл этого члена достаточно интуитивно можно представить именно как утекание каждой точки воды по вектору её скорости. Однако, в общем случае производная векторного поля \(\vec u\) по направлению \(\vec v\) обозначается как \((\vec v \cdot \vec \nabla)\vec u\) и обозначает, как меняется функция \(\vec u\) в направлении \(\vec v\) для этой точки.

Слагаемое же \(-\frac<1><\rho>\vec \nabla p\) является ускорением, которое получает жидкость в точке из-за градиента давления.

Оператор \(\vec \nabla\) , действующий на скалярное поле(например, давление), называется градиентом. Если слева от некоторой точки давление больше, чем справа, то градиент в ней будет направлен вправо и будет увлекать за собой жидкость в этом направлении. Например, ветер всегда дует в направлении, обратном градиенту давления воздуха (отсюда и минус). Электрический ток течёт в направлении градиента электрического потенциала:
\(E=\vec \nabla \phi\)

Второе уравнение \(\vec \nabla \vec u = 0\) называется уравнение непрерывности, а оператор \(\vec \nabla\) здесь действует на вектор и называется дивергенцией.

Оператор дифференцирования, действующий на вектор, называется дивергенцией. Дивергенция, равная нулю, говорит, что для каждого маленького кубика сколько в него жидкости втекает, столько и вытекает. А так как любой объём можно разбить на маленькие кубики, то свойство будет справедливо и для объёма любой формы. Это свойство называют также условием несжимаемости, так как если бы в какой-то объём втекало больше жидкости, чем вытекало, это бы означало, что жидкость в объёме накапливается, сжимаясь. Другой случай применения дивергенции, который может помочь её представить — это теорема Гаусса:
\(\vec \nabla E=\rho\)
Эта теорема говорит, что напряжённость электрического поля, которая «вытекает» из некоторого объёма, всегда вызвана электрическим зарядом плотности \(\rho\) внутри этого объёма. Если в объёме заряда нет, то и дивергенция нулевая.

То есть, одним предложением уравнение Навье-Стокса можно описать так: темп изменения скорости определяется течением и градиентом давления, но жидкость при этом не может сжиматься.

Классическое решения уравнения Навье-Стокса

Посмотрим теперь, как это уравнение можно программно решить. Для этого можно использовать подход, который называется расщеплением — разбить сложный физический процесс, состоящий из нескольких элементарных, на отдельные чередующиеся стадии и считать, что на каждой стадии работает только один элементарный процесс, а остальные выключены. Как ни странно, можно доказать (см. статью выше), что это — на самом деле математически обоснованная стратегия. Поэтому будем считать, что состояние скоростей для каждой точки в текущий момент времени \(\vec u(\vec x, t)\) нам известно. А для расчёта состояния в следующий момент времени \(t+dt\) , разобьём сложный процесс гидродинамической эволюции на простые стадии:
1) снесём поле скоростей по течению. это может немного «сжать» жидкость.
2) найдём такое давление, чтобы жидкость «расжалась».
Первый шаг называется адвекцией, второй — проекцией.

Адвекция

Адвекция, или течение, можно приближённо посчитать достаточно легко — если известно, что в точке \(\vec x\) , в момент времени \(t\) скорость равна \(\vec u(\vec x, t)\) , то в момент времени \(t+dt\) скорость в неё притечёт жидкость из точки \(\vec x — \vec u(x, t)\cdot dt\) .
\(\vec u^*(\vec x, t+dt)=\vec u(\vec x — \vec u(\vec x, t), t)\)
То есть мы получили промежуточное значение скорости, котороже уже утекло по течению, но теперь в нём нарушено условие непрерывности.

Это особенно удобно программируется на GPU, так как это можно посчитать, если хранить скорость в текстуре и её обновлять, просто читая тексели со смещением \(- \vec u(x, t)\cdot dt\) и используя стандартную аппаратную линейную интерполяцию.

Проекция

Проекция берёт скорость, для которой нарушено условие непрерывности \(\vec u^*\) и ищет такое давление, которое её «выправит» до нормальной скорости \(\vec u\) . Умные мужики доказали, что такое поле можно найти единственным образом и оно всегда будет градиентом некоторого скалярного поля (давления, в нашем случае):
\(\vec u(\vec x, t+dt)=\vec u^*(\vec x, t+dt) + \vec \nabla p\)
Помножим обе стороны этого равенства на оператор дифференцирования:
\(\vec \nabla \vec u(\vec x, t+dt)=\vec \nabla \vec u^*(\vec x, t+dt) + \vec \nabla^2 p\)
«ПОГОДИ-КА СУСЕЛ, ЭТО ЕЩЁ ЧТО» — можете меня спросить вы. Всё по порядку, но на самом деле отсюда для общего понимания достаточно знать, что если \(\vec u^*(\vec x)\) известно(а оно известно), то отсюда можно найти давление \(p(\vec x)\) . Если вспомнить, что в нашем случае дивергенция скорости равна нулю, то остаётся вот такое выражение.
\(\vec \nabla^2 p=-\vec \nabla u^*\)

В правой части этого равенства стоит дивергенция скорости, которую можно легко приблизительно посчитать, если известна скорость \(\vec u^*\) (а она известна). В левой части стоит штука, которая называется лапласианом давления.

Лапласиан — это оператор дифференцирования (ещё называется оператор набла) в квадрате, то есть применённый дважды к скалярному полю. Первый раз применяем оператор дифференцирования — получаем градиент. Второй раз — получаем дивергенцию. Таким образом оператор лапласа — это дивергенция градиента скалярного поля. Его можно представить как изменение потока скорости через маленький кубик, которое будет вызвано давлением в точке. Ещё одна аналогия — как поменяется дивергенция электрического поля в объёмчике, если в него положить заряд плотностью \(\rho\) (опять же, теорема Гаусса):
\(\vec nabla \vec E = \rho\) , \(\vec nabla \phi=\vec E\) => \(\vec nabla^2 \vec phi = \rho\)

Уравнение вида «лапласиан чего-то неизвестного равен чему-то известному» называется уравнением Пуассона. Что бы это ни значило, существует стандартный итеративный алгоритм, который позволяет его решить, то есть найти такое давление, чтобы его лапласиан был равен чему угодно. «Что угодно» мы знаем — это дивергенция промежуточной скорости, поэтому считаем по ней давление. Далее для давления считаем градиент и вычитаем результат из промежуточной скорости, чтобы получить окончательную скорость для следующего шага по времени:
\(\vec u=\vec u^* + \vec \nabla p\)

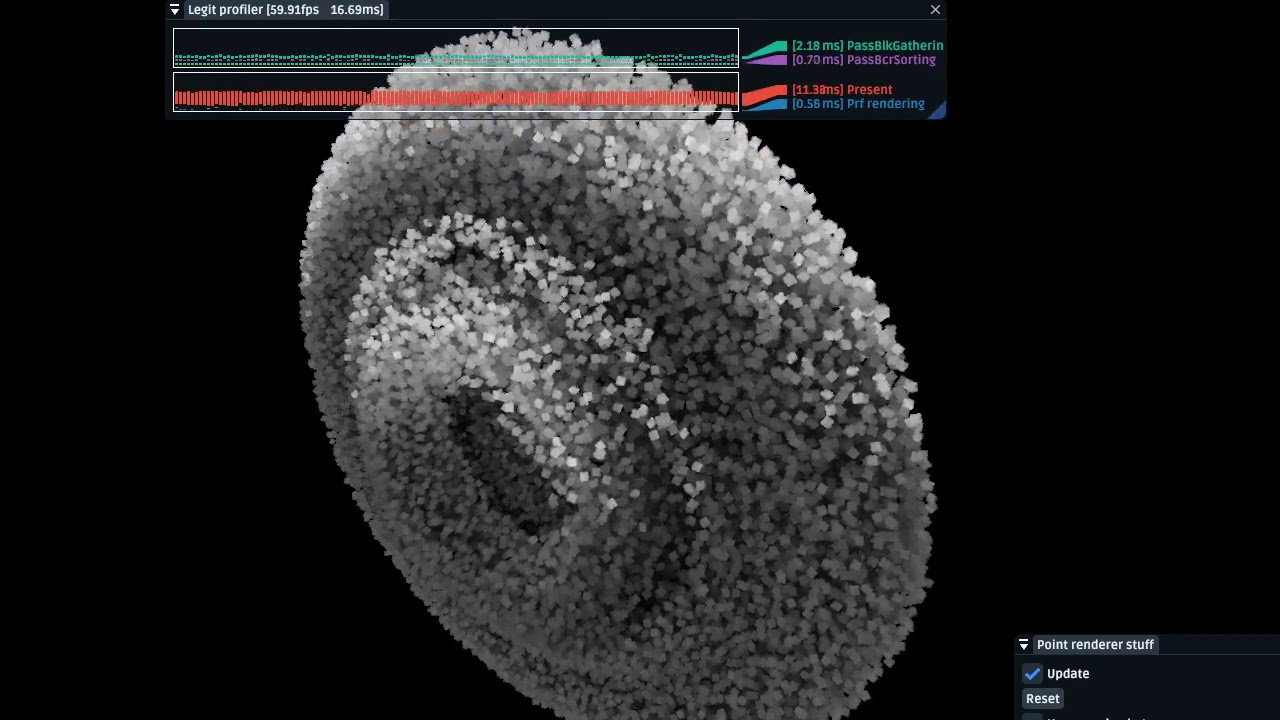
Шаги адвекции и проекции повторяем до посинения, рассчитывая всё дальше и дальше эволюцию поля течений по времени. Для визуализации можно, например, напускать частиц, которые могу сноситься этим полем скоростей. Результат выглядит так:

Важно понять, что в этом видосе, равно как и во всех остальных гифках этой статьи, жидкость на самом деле находится в большом кубе (границы которого не показаны), а не только там, где видны частицы. Частицы только уносятся полем скоростей, как, например, частицы дыма уносятся полем скоростей воздухе. Сами частицы никакой роли в физике процесса не играют и только позволяют относительно наглядно его продемонстрировать. Частицы обычно добавляются заранее туда, где ожидаются какие-то интересные турбулентности.

Важные особенности классического подхода

«Всё здорово, сусел, но в названии статьи ты написал что-то там про Шрёдингера! Он вообще где? Зачем нам это всё?» — спросите вы. Вопрос резонный. Но всю крутость подхода со Шрёдингером можно осознать, только если иметь представление о слабых сторонах классического солвера, который мы рассмотрели в предыдущей главе. В чём же они заключаются? Давайте об этом поговорим.

Основа любого расчётного метода — это то, как в нём представлены моделируемые данные. В рассмотренном нами подходе мы храним значение скорости для каждой точки. Например, в текселях двумерной или трёхмерной текстуры. Этот способ здорово работает, если требуется описать ровное поле течений, в котором нет особенностей (так называются завихрения и разные другие неоднородности). Неоднородностей обычно нет в вязких жидкостях вроде мёда или майонеза, поэтому метод очень здорово подходит, чтобы моделировать майонез. Но более текучие среды (например, вода, воздух и дым) отличаются тем, что в них существенную роль играют злополучные турбулентные течения — мелкие завихрения, имеющие очень сложную и нерегулярную структуру, даже образующие фракталы, которые очень неудобно описывать просто их значениями в каждой точке текстуры/массива. Если попытаться их моделировать, то все мелкие особенности быстро смазываются и расплываются, что соответствует поведению вязкой жидкости. Такое поведение называется численной вязкостью — это вязкость жидкости, которая появляется не потому что она является частью уравнения, которое мы решаем, а это паразитная вязкость, всплывающая как паразитное следствие нашего метода решения. Более того, напомню, что первое, что мы сделали, не успев взглянуть на уравнение Навье-Стокса — выкинули из него вязкость, так в ней недостатка точно не будет.

А вот избавиться от вязкости гораздо труднее, чем случайно её посчитать. Один из способов — это измельчать расчётную сетку. Чтобы таким методом получить что-то хоть как-то похожее на дым, понадобится сетка минимум 1024x1024x1024, то есть как минимум гигабайт памяти, если хранить по 1 байту на узел. А хранить захочется как минимум трёхкомпонентную скорость, то есть, скорее всего, 32 гигабайта в сумме. Это не только не разумно с точки зрения затрат памяти, это ещё и очень медленно. Другой способ — это представлять скорость не её направлением в каждой точке, а как сумму маленьких элементарных вихрей. Этот метод называется также методом дискретных вихрей. В нём вообще всё не так просто с процессами порождения новых вихрей и удаления старых, с поддержанием нужной плотности (так как вихри друг друга уносят, как частицы) и ещё миллион проблем, можете сами почитать, если интересно. Другой подход основан на том, что в реальных течениях вихри имеют свойство образовывать вращающиеся нити. Представьте медленно движущийся жгут, вокруг которого быстро вращается жидкость. Если такой жгут замыкается в кольцо, получается тороидальный вихрь, образующий знакомое кольцо дыма:

Существуют подходы, которые вместо хранения величины скорости в точках, хранят именно параметры таких жгутов. Но такие методы полагаются на топологию, поэтому в них необходимо считать, как жгуты взаимодействуют, сливаются, распадаются и вообще происходящее быстро теряет простоту и наглядность.

Однако, у классического метода есть одно очень важное положительное свойство — в нём вообще нет параметров. Обратите внимание, что для расчёта используется только скорость и больше вообще ничего — ни вязкости, ни даже плотности. В уравнении Навье-Стокса без вязкости есть плотность, но её можно «спрятать» в нормировку давления, поэтому можно сказать, что в исходном уравнении параметров также нет. Забегая вперёд, замему, что в солвере на уравнении Шрёдинге будет параметр. Загадочный.

На следующей странице мы рассмотрим, как же применить уравнения Шрёдингера, чтобы смоделировать тот же самый процесс, и какой в этом профит. Будет много картинок.