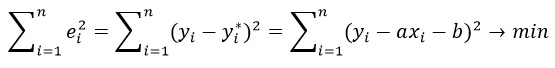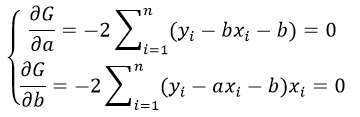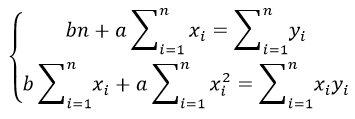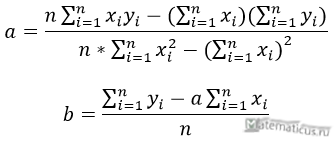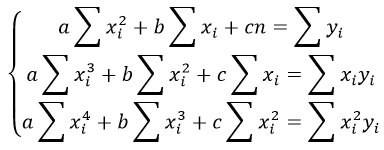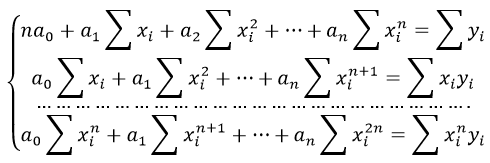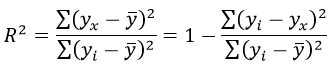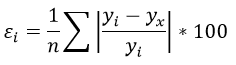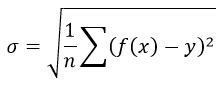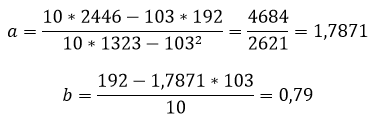Метод наименьших квадратов регрессия
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R 2 :
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
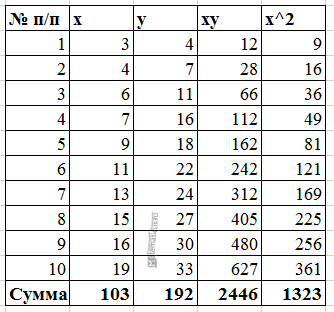
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
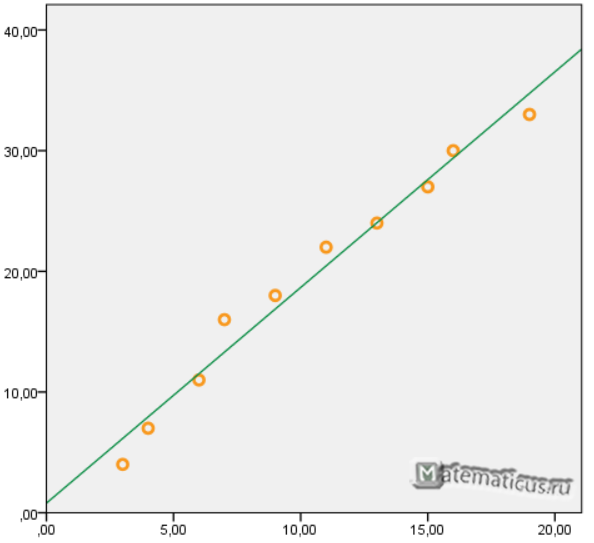
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Шпаргалка по «Эконометрике»
Автор: Пользователь скрыл имя, 13 Сентября 2013 в 13:45, шпаргалка
Краткое описание
Работа содержит ответы на 182 вопроса по дисциплине «Эконометрика».
Файлы: 1 файл
пучок эконометрика.docx
Для получения качественных оценок параметров этой модели .
- требуется подобрать соответствующую подстановку.
135. Зависимость валового национального продукта от денежной массы характеризуется линейно-логарифмической эконометрической моделью, которая имеет вид:
136. С помощью подходящих преобразований исходных переменных регрессионная зависимость представляется в виде линейного соотношения между преобразованными переменными. Этот процесс называется +++ модели.
137. Укажите верные характеристики коэффициента эластичности:
- коэффициент эластичности показывает на сколько процентов изменится значение результирующего фактора при изменении на один процент объясняющего фактора.
138. Временным рядом является совокупность значений .
- экономического показателя за несколько последовательных моментов (периодов) времени.
139. Автокорреляцией уровней временного ряда называют
- корреляционную зависимость между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на один или несколько периодов времени.
140. Гипотеза об аддитивной структурной схеме взаимодействия факторов, формирующих уровни временного
ряда, означает правомерность следующего представления
- уровень временного ряда = тренд + конъюнктурная компонента + сезонный фактор + случайная компонента.
141. Эконометрическая модель, являющаяся системой одновременных уравнений, состоит в общем случае
- из поведенческих уравнений и тождеств.
142. Система уравнений, в которых каждая эндогенная переменная рассматривается как функция только
предопределенных переменных, называется системой +++ уравнений.
143. Анализ возможности численной оценки неизвестных коэффициентов структурных уравнений по оценкам коэффициентов приведенных уравнений составляет:
144. С помощью традиционного метода наименьших квадратов нельзя определить параметры уравнений, входящих в систему ___ уравнений:
145. Отбор факторов в эконометрическую модель множественной регрессии может быть осуществлен на основе:
- матрицы парных коэффициентов корреляции
- сравнения остаточной дисперсии до и после включения фактора в модель
146. Фиктивная переменная может принимать значения:
147. В линейном уравнении парной регрессии переменными не являются:
148. Метод наименьших квадратов применим к уравнениям регрессии, .
- которые отражают линейную зависимость между двумя экономическими показателями
- которые отражают нелинейную зависимость между двумя экономическими показателями, но могут быть приведены к линейному виду
149. Предпосылками метода наименьших квадратов(МНК) являются следующие:
- гомоскедастичностью остатков
- отсутствие автокорреляции в остатках
150. Несмещенность оценки характеризуется.
- равенством нулю математического ожидания остатков
- отсутствием накопления остатков при большом числе выборочных оцениваний
151. Обобщенный метод наименьших квадратов подразумевает .
- преобразование переменных
- введение в выражение для дисперсии остатков коэффициента пропорциональности
152. Для зависимости спроса на некоторый товар от цены за единицу товара и дохода потребителя получено уравнение регрессии вида . Парными коэффициентами корреляции могут быть.
153. Значение коэффициента детерминации составило 0,9; следовательно, отношение ___ дисперсии к общей дисперсии равно ___.
154. Критическое (табличное) значение F-критерия является пороговым значением для определения .
- значимости (существенности) моделируемой связи между зависимой и совокупностью независимых переменных экономической модели
- статической значимости построенной модели
155. Пусть -рассчитанная для коэффициента статистики Стьюдента, а — критическое значение этой статистики. Коэффициент регрессии считается статистически значимым, если выполняются следующие неравенства:
156. Примером нелинейного уравнения регрессии не является уравнение вида .
157. Установите соответствие между названием модели и видом ее уравнения:
Параболическая модель третьего ряда(1)
158. Примерами уравнения регрессии, нелинейных относительно объясняющих переменных, но линейных по оцениваемым параметрам, являются .
159. Качество подбора нелинейного уравнения регрессии можно охарактеризовать на основе показателей .
- коэффициента эластичности
- индекса детерминации
- средней ошибки аппроксимации
160. Факторы, описывающие трендовую компоненту временного ряда, характеризуется .
- долговременным воздействием на экономический показатель
- возможностью расчета значения компоненты с помощью аналитической функции от времени
161. Укажите справедливые утверждения по поводу коэффициента автокорреляции уравнений временного ряда:
- характеризует тесноту линейной связи между уровнями ряда
- равен коэффициенту линейной корреляции между последовательными уровнями ряда
162. Построение модели временного ряда может быть осуществлено с использованием .
- аддитивной модели
- мультипликативной модели
163. Основные характеристики строго стационарного переменного ряда х(t)- его средняя величина и дисперсия .
164. Система эконометрических уравнений включает в себя следующие переменные:
165. Выберите верные утверждения по поводу системы одновременных уравнений
- в ней одни ите же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях — в правую часть системы
- может быть представлена в структурной форме модели и в приведенной форме
166. Эндогенные переменные .
- могут коррелировать с ошибками регрессии
167. Применение косвенного метода неменьших квадратов возможно для идентифицируемой системы одновременных уравнений, так как в идентифицируемых системах .
- возможно однозначное выражение коэффициентов структурной формы через коэффициенты приведенной формы системы
168. К видам эконометрических моделей по типам зависимости относятся модели:
- линейной регрессии
- нелинейной регрессии
169. Стахостический стационарный в сильном смысле процесс, включая временной ряд, независимо от рассматриваемого периода времени имеет постоянную величину:
- среднего значения процесса
- дисперсии процесса
- автоковариации процесса
170. Стахостический стационарный в слабом смысле процесс, включая временной ряд, независимо от рассматриваемого периода времени и длины лага между рассматриваемыми переменными, имеет постоянную величину:
- дисперсии процесса
- среднего значения процесса
171. В стационаром временном ряде отсутствуют:
- тренд
- систематическое изменение дисперсии
- строго периодичные флуктцации
172. При нахождении распределенного лага методом Алмон необходимо меть предварительную информацию:
- о величине лага
- о степени полинома, описывающего структуру лага
173. В методе Койка уменьшение во времени лаговых воздействий фактора на результат описывается формулой:
174. Нахождение тренда временного ряда путем аналитического выравнивания включает в себя этапы:
- спецификации, параметризации и последующей верификации различных функций
175. Выбор мультипликативной модели временного ряда производится, если сезонные колебания имеют:
- возрастающую или уменьшающуюся амплитуду колебаний
176. Если в коррелограмме наибольшее значение имеет коэффициент автокорреляции первого порядка то исследуемый временной ряд содержит только:
177. Если в коррелограмме наибольшее значение имеет коэффициент автокорреляции порядка то исследуемый временной ряд содержит только:
- циклические колебания с периодичностью
178. Если в коррелограмме ни один из коэффициентов автокорреляции не является значительным, то структура временного ряда:
- не содержит тенденции (тренд)
- содержит сильную нелинейную тенденцию
- не содержит циклической составляющей
179. Формула для определения сглаженного значения уровня временного ряда при использовании скользящей взвешенной имеет вид:
180. Формула для определения сглаженного значения уровня временного ряда при использовании скользящей средней имеет вид:
181. Формула для определения значения уровня временного ряда при использовании экспоненциального сглаживания имеет вид:
182. Выбор мультипликативной модели временного ряда производится, если сезонные колебания имеют:
- возрастающую или уменьшающуюся амплитуду колебаний
Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
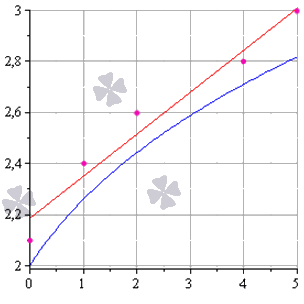
Как изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
http://student.zoomru.ru/ekonom/shpargalka-po-jekonometrike/257842.2241353.s3.html
http://zaochnik.com/spravochnik/matematika/stati/metod-naimenshih-kvadratov/