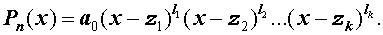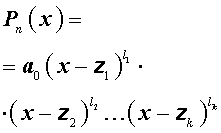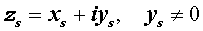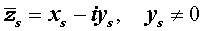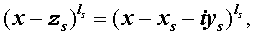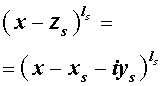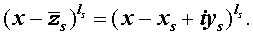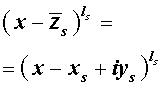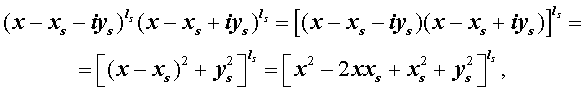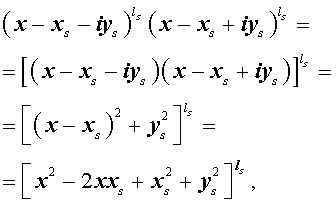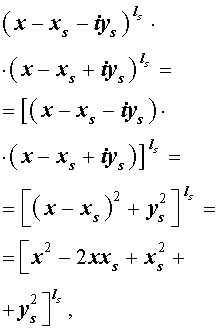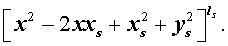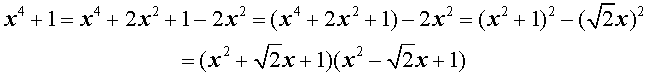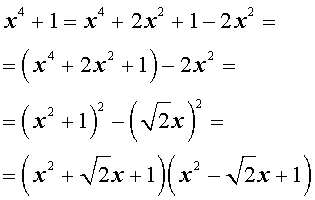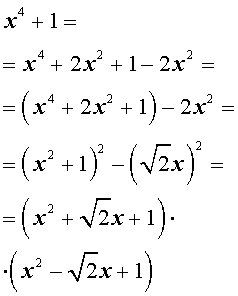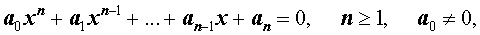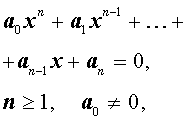Многочлены и алгебраические уравнения комплексные числа

Многочлены и алгебраические уравнения комплексные числа

КОМПЛЕКСНЫЕ ЧИСЛА И МНОГОЧЛЕНЫ

Оглянемся назад: после первой, вводной, темы мы занимались линейной алгеброй (главы 2 и 3). Затем применяли построенный алгебраический аппарат к геометрическим задачам (главы 4 и 5). Но подробно изучить мы смогли только прямые и плоскости, то есть линейные объекты, задаваемые уравнениями 1-й степени. Для работы с более сложными линиями и поверхностями нам потребуются новые алгебраические понятия и методы.

Кроме того, важным направлением алгебры является изучение уравнений n-й степени с одним неизвестным:

Выражение в левой части этого уравнения называется многочленом от переменной x. Изучению многочленов и расширению, обобщению понятия числа посвящается эта глава.

6.1. Поле комплексных чисел

Во введении мы проследили, как происходило развитие понятия числа: от натуральных чисел к целым, рациональным, действительным числам. Сделаем ещё один шаг, от действительных чисел перейдём к комплексным.

Пусть a, b — действительные числа, i — некоторый символ. Комплексным числом называется выражение вида a + bi.

Замечание. Можно было бы использовать любой другой значок, и записывать комплексные числа так: a + bd. Мы пользуемся общепринятыми обозначениями. Сначала, возможно, будет непривычно рассматривать числа 2 + 3i, . и так далее. Однако подумайте: переход от целых чисел к дробям был не менее трудным: одно число стали писать выше, другое ниже, между ними — черта. Теперь нам это кажется естественной записью.

Комплексные числа и многочлены

Вы будете перенаправлены на Автор24

После долгих сомнений, которые длились более столетия, известные математики пришли к единому заключению, что необходимо ввести некоторый новый вид чисел, который назвали комплексными числами.

Выражение вида $z=a+bi$, где $a$ и $b$ — вещественные числа, а $i$ — «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt <-1>$ или $i^ <2>=-1$.

Комплексное число вида $\overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Записать комплексно-сопряженные числа для заданных комплексных чисел:

$1) z_ <1>=12+3i; 2) z_ <2>=5; 3) z_ <3>=-2i.$

Для комплексного числа $z=a+bi$ комплексно-сопряженным будет являться число $\overline=a-bi$.

Для числа $z_ <1>=12+3i$ получим $\overline >=12-3i$.

Для числа $z_ <2>=5$ получим $\overline >=5$.

Для числа $z_ <3>=-2i$ получим $\overline >=2i$.

Некоторые комплексные числа $z_ <1>=a_ <1>+b_ <1>i$ и $z_ <2>=a_ <2>+b_ <2>i$ называются равными, если выполняются следующие равенства $a_ <1>=a_ <2>,b_ <1>=b_ <2>$. Обозначение: $z_ <1>=z_ <2>$.

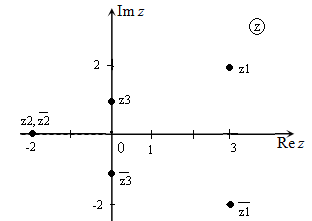
Любое комплексное число можно изобразить на плоскости, которую принято называть комплексной плоскостью. Комплексная плоскость аналогична прямоугольной декартовой системе координат, исключение составляют только названия осей:

• действительная ось (соответствует оси абсцисс);
• мнимая ось (соответствует оси ординат) (рис.1).

Выделяют три формы представления (записи) комплексных чисел:

• алгебраическая;
• тригонометрическая;
• показательная.

Алгебраическая форма записи

Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:

$a$ — вещественная (действительная) часть, обозначение $Rez=a$;

$b$ — мнимая часть, обозначение $Imz=b$.

Тригонометрическая форма записи

Запись комплексного числа $z$ в виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ — модуль комплексного числа $z$, определяемый формулой $r=|z|=|a+bi|=\sqrt +b^ <2>> $, а $\varphi $ — аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac $.

Показательная форма записи

Запись комплексного числа $z$ в виде $z=r\cdot e^ $ называется показательной формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt +b^ <2>> $, $\varphi $ — аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac $.

Над комплексными числами можно выполнять следующие действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Операции над комплексными числами

Сумма

Суммой двух заданных комплексных чисел $z_ <1>=a_ <1>+b_ <1>i$ и $z_ <2>=a_ <2>+b_ <2>i$ является комплексное число, которое определяется равенством $z_ <1>+z_ <2>=(a_ <1>+b_ <1>i)+(a_ <2>+b_ <2>i)=(a_ <1>+a_ <2>)+(b_ <1>+b_ <2>)\cdot i. $

Разность

Разностью двух заданных комплексных чисел $z_ <1>=a_ <1>+b_ <1>i$ и $z_ <2>=a_ <2>+b_ <2>i$ является комплексное число, которое определяется равенством $z_ <1>-z_ <2>=(a_ <1>+b_ <1>i)-(a_ <2>+b_ <2>i)=(a_ <1>-a_ <2>)+(b_ <1>-b_ <2>)\cdot i.$

Произведение

Произведением двух заданных комплексных чисел $z_ <1>=a_ <1>+b_ <1>i$ и $z_ <2>=a_ <2>+b_ <2>i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^ <2>=-1$.

Произведением двух заданных комплексных чисел $z_ <1>=r_ <1>\cdot (\cos \varphi _ <1>+i\sin \varphi _ <1>)$ и $z_ <2>=r_ <2>\cdot (\cos \varphi _ <2>+i\sin \varphi _ <2>)$ является комплексное число, которое определяется равенством $z_ <1>\cdot z_ <2>=r_ <1>\cdot r_ <2>\cdot [\cos (\varphi _ <1>+\varphi _ <2>)+i\sin (\varphi _ <1>+\varphi _ <2>)].$

Частное

Частным двух заданных комплексных чисел $z_ <1>=r_ <1>\cdot (\cos \varphi _ <1>+i\sin \varphi _ <1>)$ и $z_ <2>=r_ <2>\cdot (\cos \varphi _ <2>+i\sin \varphi _ <2>)$ является комплексное число, которое определяется равенством $z_ <1>\cdot z_ <2>=\frac > > \cdot [\cos (\varphi _ <1>-\varphi _ <2>)+i\sin (\varphi _ <1>-\varphi _ <2>)].$

Степень порядка

Степенью порядка $n$ комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством $z^ =r^ \cdot (\cos n\varphi +i\sin n\varphi _ <1>). $

Данная формула называется формулой Муавра.

Корень

Корнем $n$-й степени комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством $\sqrt[] =\sqrt[] \cdot (\cos \frac<\varphi +2\pi k> +i\sin \frac<\varphi +2\pi k> ),\, \, \, k=0..n-1.$

Готовые работы на аналогичную тему

Выполнить действия: 1) $z_ <1>+z_ <2>$; 2) $z_ <1>-z_ <2>$; 3) $z_ <1>\cdot z_ <2>$ для комплексных чисел $z_ <1>=1+3i$ и $z_ <2>=1-2i$.

$3) z_ <1>\cdot z_ <2>=(1+3i)\cdot (1-2i)=1\cdot 1+1\cdot 3i-1\cdot 2i-3\cdot 2\cdot i^ <2>=1+3i-2i+6=7+i $

Выполнить умножение и деление заданных комплексных чисел:

$z_ <1>=\sqrt <3>\cdot (\cos \pi +i\cdot \sin \pi )$ и $z_ <2>=\sqrt <3>\cdot (\cos \pi +i\cdot \sin \pi )$.

1) $ \cdot z_ <2>=\left(\sqrt <3>\cdot (\cos \pi +i\cdot \sin \pi )\right)\cdot \left(\sqrt <3>\cdot (\cos \pi +i\cdot \sin \pi )\right)=\sqrt <3>\cdot \sqrt <3>\cdot [\cos (\pi +\pi )+i\cdot \sin (\pi +\pi )]=> \\ <=3\cdot (\cos 2\pi +i\cdot \sin 2\pi )>$

2) $ =\left(\sqrt <3>\cdot (\cos \pi +i\cdot \sin \pi )\right)\div \left(\sqrt <3>\cdot (\cos \pi +i\cdot \sin \pi )\right)=\frac <\sqrt<3>> <\sqrt<3>> \cdot [\cos (\pi -\pi )+i\cdot \sin (\pi -\pi )]=> \\ <=1\cdot (\cos 0+i\cdot \sin 0)=\cos 0+i\cdot \sin 0>$

Многочлен

Многочленом $n$-ой степени называется функция

где коэффициенты $a_ <0>,a_ <1>,a_ <2>. a_ ,a_ $ — постоянные комплексные числа, $a_ \ne 0$, $z\in Z$ — комплексная переменная. Число $z_ <0>$, при котором заданный многочлен принимает нулевое значение ($P_ (z_ <0>)=0$), называется корнем этого многочлена.

Любой многочлен степени $n$ может быть представлен как разложение многочлена на $n$ линейных сомножителей вида $z-a$ и множитель, который равен коэффициенту при $z^ $:

$$P_ (z)=A_ <0>\cdot (z-a_ <1>)\cdot (z-a_ <2>)\cdot . \cdot (z-a_ ), $$

где $a_ <1>,a_ <2>. a_ $ — корни многочлена.

Если в разложении многочлена степени $n$ на линейные множители

$P_ (x)=A_ <0>\cdot (z-a_ <1>)\cdot (z-a_ <2>)\cdot . \cdot (z-a_ ), (*) $

некоторые линейные сомножители оказываются одинаковыми, то данные множители можно объединить, тогда разложение заданного многочлена на сомножители будет иметь следующий вид:

В формуле (*) корни многочлена $a_ <1>,a_ <2>. a_ $ могут быть не только вещественными, но и комплексными числами.

Для многочленов определены следующие операции: вычитание, сложение, умножение. Операция деления многочленов определена не для любых двух многочленов, однако, как и для целых чисел, имеется возможность выполнить деление с остатком.

Разложение многочленов на множители. Формулы Виета

Алгебраические уравнения

Основная теорема алгебры. Разложение многочленов на линейные множители в комплексной области

Разложение на множители многочленов с действительными коэффициентами

Теорема (формулы) Виета

Алгебраические уравнения

Пусть n – произвольное натуральное число. Рассмотрим многочлен n – ой степени от переменной x

Заметим, что в этом случае коэффициент a₀ отличен от нуля, и введем следующее определение.

Определение 1 . Алгебраическим уравнением степени n с неизвестным x называют уравнение вида

Определение 2 . Корнем уравнения (3) называют вещественное или комплексное число α , для которого

Определение 3 . Число α называют корнем кратности k уравнения (3), если справедливо равенство

.

Разложение многочленов на множители в комплексной области

Основная теорема алгебры (теорема Гаусса) утверждает, что любое алгебраическое уравнение вида (3) имеет n корней, при условии, что каждый корень считается столько раз, какова его кратность.

– полный набор корней уравнения (3), а

– их кратности, то, во-первых,

а, во-вторых, справедливо равенство

Замечание . Линейными множителями называют многочлены первой степени

входящие в формулу (4), а саму формулу (4) называют формулой разложения многочленов на линейные множители в комплексной области .

Разложение на множители многочленов с действительными коэффициентами

Рассмотрим теперь многочлены степени 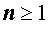, все коэффициенты которых являются вещественными числами.

Тогда справедливо следующее

Утверждение . Если комплексное число

является корнем кратности l_s многочлена с вещественными коэффициентами, то и комплексно сопряженное число

является корнем этого многочлена, причем тоже кратности l_s .

Из утверждения вытекает, что в разложение (4) степень каждого бинома, содержащая комплексный корень z_s и имеющая вид

входит в паре со степенью бинома, содержащей комплексно сопряженный корень 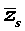и имеющей вид

то произведение каждой пары биномов (5) и (6), входящей в формулу (4), даёт степень квадратного трехчлена с вещественными коэффициентами:

Следствие . Каждый многочлен ненулевой степени, коэффициенты которого являются вещественными числами, разлагается на множители, являющиеся многочленами с вещественными коэффициентами первой или второй степени.

Пример . Разложить на множители многочлен четвертой степени

Теорема (формулы) Виета

Снова рассмотрим уравнение n – ой степени от переменной x

и, немного изменив предыдущие обозначения, предположим, что

— его корни, причем в записи (8) каждый корень взят столько раз, какова его кратность.

Тогда из формулы (4) вытекают следующие равенства, которые называют формулами Виета для уравнения n – ой степени :