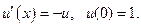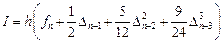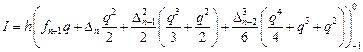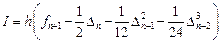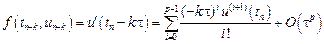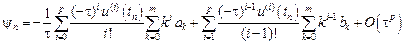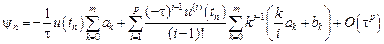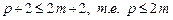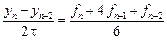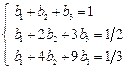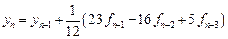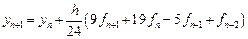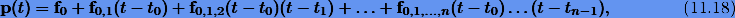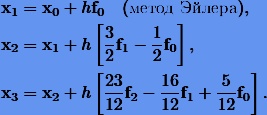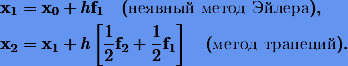Общая формулировка многошаговых методов
Многошаговые методы
Решения задачи коши
9.1. Метод “предиктор-корректор” 2
9.2. Общая формулировка многошаговых методов 4
9.3. Устойчивость и сходимость разностных методов 7
9.1. Метод “предиктор-корректор”
В одношаговых методах значение yn+1 определяется лишь значениями tn, yn и значением шага приращения аргумента h. В многошаговых методах используется также информация в предыдущих точках yn-1, yn-2,
Многошаговые методы строятся на равномерной сетке
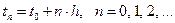
Обозначим: 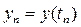
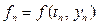
Линейный m-шаговый метод можно описать формулой:

Многошаговые методы не являются самостартующими. Для использования m-шагового метода необходимо предварительно задать m предыдущих значений y. Однако после того как многошаговый метод стартует, он работает быстрее, чем одношаговый. Например, при использовании метода Рунге-Кутта-Фельберга на каждом шаге приращения аргумента требуется шесть раз вычислять правую часть дифференциального уравнения 
Еще одним ограничением использования многошаговых методов является наличие равномерной сетки. Однако это ограничение легко преодолевается, например, с помощью интерполяции.
Многошаговые методы используются при решении жестких уравнений.
Порядок многошагового метода может выбираться автоматически и динамически изменяться.
Если 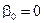
Если 
Частным случаем многошаговых методов являются методы Адамса:
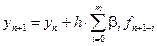
Методы Адамса также могут быть явными и неявными.
Трудности использования неявной формулы преодолевается в методе Предиктор–Корректор. В этом методе значение неизвестной функции в каждой точке сетки вычисляется дважды. Сначала вычисляется новое значение неизвестной функции 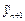

Простейшим примером метода Предиктор–Корректор является второй модифицированный метод Эйлера, который можно описать с помощью последовательности формул:

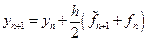
Метод Эйлера является одношаговым методом. Для построения многошаговых методов вновь используем утверждение: решение задачи Коши эквивалентно решению интегрального уравнения
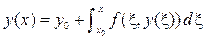
Для приближенного решения задачи Коши аппроксимируем подынтегральную функцию в формуле (9.3) с помощью интерполяционного многочлена. Интерполяционный многочлен Ньютона степени m для интерполирования назад от точки xn можно записать следующим образом

В формуле (9.4) 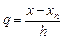

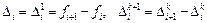

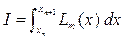
Найдем вначале формулы для двухшагового метода m=2. В качестве подынтегральной функции в формуле (9.6) будем использовать интерполяционный многочлен Ньютона первой степени.
Для вывода формулы предиктор вычислим интеграл (9.6) на отрезке экстраполяции 

и 
Подставив найденное значение интеграла в формулу (9.3), получим экстраполяционную формулу – формулу предиктор:

При выводе формулы корректор используем многочлен Ньютона для интерполирования от точки xn+1. Соответственно, в формуле (9.7) все индексы нужно увеличить на 1, а пределы интегрирования изменить на 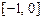
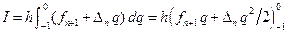
Подставив найденное значение интеграла в формулу (9.3), получим интерполяционную формулу – формулу корректор:
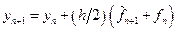
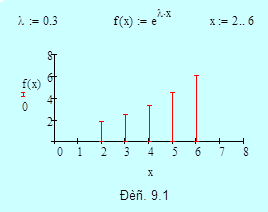
С помощью двухшагового метода предиктор-корректор найдем решение начальной задачи:
Точное решение представляет собой экспоненту 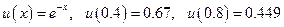
Выберем шаг приращения 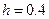
Начальное условие: 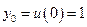
Дополнительное условие: 
С помощью формул (9.8) и (9.10) вычислим значение 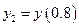
По формуле предиктор получаем: 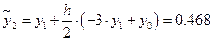
По формуле корректор уточняем решение: 
Для сравнения приведем расчеты значения 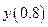

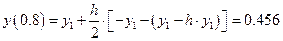
На практике обычно применяется четырехшаговый метод Адамса. Найдем формулы для четырехшагового метода. Повторяем весь ход рассуждений, использованных при выводе формул 2-шагового метода, но в отличие от предыдущего используем теперь многочлен Ньютона третьей степени.
Вывод формулы предиктор.
Подставив найденное значение интеграла в формулу (9.3), получим с учетом выражений (9.5) для конечных разностей формулу предиктор – формулу Адамса-Башфорта (Adams-Bashforth):
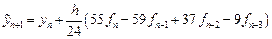
Вывод формулы корректор.
Аналогично предыдущему с учетом (9.3) и (9.5) получим формулу корректор – формулу Адамса-Мультона (Adams-Moulton):
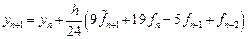
Общая формулировка многошаговых методов
Для решения задачи Коши
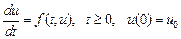
введем сетку с постоянным шагом 

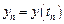

Линейным m-шаговым разностным методом называется система разностных уравнений
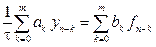
где 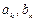
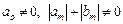
Уравнение (9.14) представляет собой рекуррентное соотношение, выражающее новое значение 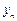
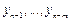
Заметим, что коэффициенты уравнения (9.14) определены с точностью до множителя. Для устранения неоднозначности будем считать, что выполнено условие нормировки

Метод называется явным, если 
Если 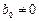
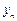

Это уравнение можно решить методом Ньютона, в качестве начального приближения взяв 
Погрешностью аппроксимации на решении или невязкой разностного метода (9.14) называется функция
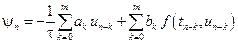
Функция невязки получается в результате подстановки точного решения дифференциального уравнения в разностное уравнение (9.14).
Подставим эти разложения в формулу для невязки
Изменим порядок суммирования. При этом во второй сумме будем суммировать по индексу i от 1 до p, соответственно уменьшив всюду индекс i на единицу.
Объединим суммы, выделив в первой сумме отдельно слагаемое с j=0.
Отсюда следует, что погрешность метода будет иметь порядок p, если выполнены условия:
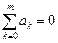
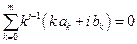

Заметим что, если в системе (9.17) отбросить последние s уравнений, то порядок метода понизится на s.
Итак, получили систему уравнений для коэффициентов ak, bk. К этим уравнениям нужно добавить еще условие нормировки (9.15): 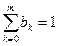
Для неявного метода имеем 2m+2 неизвестных: 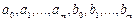
– для неявного метода порядок аппроксимации не превышает 2m.
Для явного метода имеем 2m+1 неизвестных: 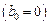
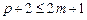
Преобразуем систему уравнений для коэффициентов ak, bk. С учетом условия нормировки уравнение 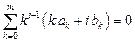
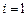
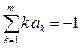
Окончательно получаем систему уравнений для коэффициентов линейного m-шагового разностного метода общего вида:
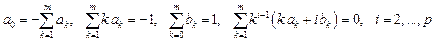
На практике часто используются методы Адамса, которые описываются формулой
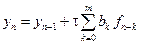
Для методов Адамса в системе (9.18) остаются только уравнения, определяющие коэффициенты bk.

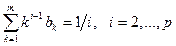
Имеем p уравнений. В случае неявного метода Адамса имеется m+1 неизвестных: 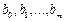
Рассмотрим варианты двухшаговых методов m=2. Максимальный порядок двухшагового метода равен p=4, так что можно написать следующую систему уравнений.
Ограничившись первыми четырьмя уравнениями этой системы, можно построить методы 2-го порядка. Если использовать пять уравнений, получим методы 3-го порядка. Система из шести уравнений определяет единственный двухшаговый метод 4-го порядка.
Варианты методов второго порядка.
1) Положим 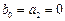
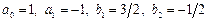

2) Положив 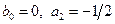

3) Положив 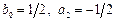
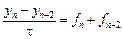
Варианты методов третьего порядка.
1) Положив 
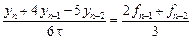
2) Если выбрать 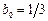

3) Выбрав 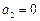
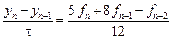
Метод четвертого порядка получим, используя все шесть уравнений:
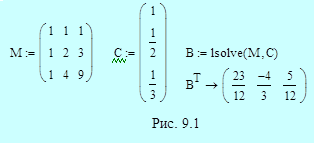
Явный трехшаговый метод имеет порядок p=3. В соответствии с формулами (9.20) для нахождения коэффициентов bk имеем систему уравнений, включающую условие нормировки и еще два уравнения для двух значений i: 
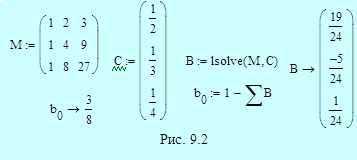
Неявный метод имеет четвертый порядок, и для коэффициентов 
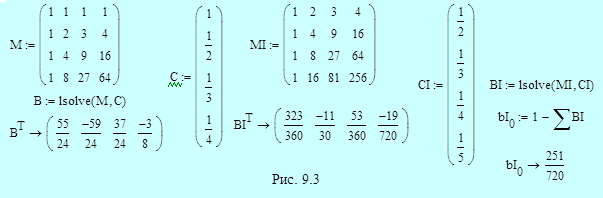 |
Пример 9.4. На рис. 9.3 приведено решение системы уравнений для коэффициентов явного и неявного четырехшаговых методов Адамса. Решение аналогично решению в примере 9.2 для трехшаговых методов. Обозначения M, C и B относятся к явному методу; обозначения MI, CI, BI и bI0 используются для описания неявного метода. Получаем в итоге:
- явный метод четвертого порядка (формула Адамса-Башфорта)
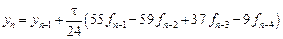
- неявный метод пятого порядка
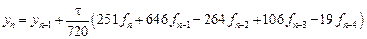
ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ
автор Авдюшев Виктор Анатольевич
11.3 Методы Адамса
Методы Рунге-Кутты — одношаговые: в них для получения решения на шаге требуется только одно решение предыдущего шага. Многошаговые методы в отличие от одношаговых используют несколько решений, вычисленных на предыдущих шагах. В начале интегрирования, когда известно только одно решение (начальное условие), первые (стартовые) решения для многошаговых методов, как правило, вычисляют с помощью одношаговых методов Рунге-Кутты. Затем на каждом следующем шаге выполняют многошаговую процедуру интегрирования.
Многошаговые методы появились гораздо раньше, чем методы Рунге-Кутты. Впервые их получил Адаме еще в 1855 г. Тем же способом, что и Адамc, выведем первое семейство многошаговых методов.
Предположим, для задачи Коши (2.7):
нам известны первые n + 1 решений 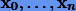

Заменим подынтегральную функцию на ее интерполирующий полином Ньютона, полученного по узловым значениям 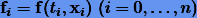
где разделенные разности вычисляются по формулам (7.10). Тогда численный аналог (11.17) будет
Согласно (11.19) для n = 0, 1, 2 получаем следующие явные формулы Адамса:
Формулы Адамса получаются при интегрировании интерполяционного многочлена (11.18) от tn до tn+1 т-е- вне интервала интерполяции. Однако, как мы знаем, вне этого интервала интерполяционный многочлен обычно дает довольно плохое приближение. Таким образом, явные методы Адамса не очень точны. Чтобы разрешить эту проблему, Адаме предложил для интерполяции использовать значение fn+1 вместо f0. В итоге, он получил неявные методы. Приведем первые из них для n = 0,1:
Итак, любой s-шаговый метод Адамса можно представить в общем виде
где bi — постоянные метода. Если bi = 0, метод — явный, иначе — неявный. Порядок метода определяется точностью интерполирующей формулы (11.18). В общем случае явный метод (11.20) имеет порядок р = s, неявный — р = s + 1.
Представление о многошаговых методах
Лекция 17
Одношаговые и многошаговые методы
Методы Рунге-Кутты
Метод Эйлера приятно радует своей простотой. Однако пример, рассмотренный в §20, наводит и на грустные размышления. Выполнив численное интегрирование уравнения 





Точка 2 пересечения касательной с вертикалью 
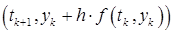

Посмотрите еще раз на рис.21.1. Не возникло ли у вас подозрения, что если провести из точки 1 прямую не под углом 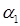

то результат (точка 3) будет лучше, чем в методе Эйлера (точка 2)? Возможно, во всяком случае, это стоит проверить.
Итак, проверяем «улучшенный» метод Эйлера, который согласно (21.4) предлагает для приближенного решения в очередной точке 
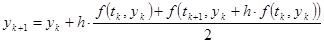
Для рассмотренной в § 20 задачи

результаты, полученные по методу (21.5), как видно из нижеследующей таблицы, совпадают с точным решением (21.6) – 
 |  |  |  |  |  |  |
| 0.0 | 0.00 | 0.0 | 0.00 | 0.2 | 0.01 | |
| 0.1 | 0.01 | 0.2 | 0.03 | 0.4 | 0.04 | |
| 0.2 | 0.04 | 0.4 | 0.08 | 0.6 | 0.09 | |
| 0.3 | 0.09 | 0.6 | 0.15 | 0.8 | 0.16 | |
| 0.4 | 0.16 | 0.8 | 0.24 | 1.0 | 0.25 | |
| 0.5 | 0.25 |
Конечно, это не означает, что метод (21.5) всегда так точен. В данном случае просто методу повезло с задачей. Метод Эйлера ‑ метод первого порядка ‑ как можно видеть из рис.20.1, заключается в замене неизвестной функции на линейную в пределах одного шага. «Улучшенный» метод Эйлера (20.5) является методом второго порядка (см, например, [17.1]). Можно показать, что формула (20.5) получена в результате аналогичной «подмены» неизвестной кривой на полином второй степени в пределах одного шага. Поскольку и искомое решение и кривая, аппроксимирующая решение, являются кривыми второго порядка, для этой конкретной задачи (20.6) значения, полученные, вообще говоря, приближенным методом, оказались точными. В общем случае полного совпадения, как правило, не бывает.
В качестве примера приведем решение обоими рассмотренными методами простого дифференциального уравнения

 |  | Точное решение  | Метод Эйлера | «Улучшенный» метод Эйлера |
| 0.0 | 1.000 | 1.000 | 1.000 | |
| 0.1 | 1.105 | 1.100 | 1.105 | |
| 0.2 | 1.221 | 1.210 | 1.220 | |
| 0.3 | 1.350 | 1.331 | 1.348 | |
| 0.4 | 1.492 | 1.464 | 1.487 | |
| 0.5 | 1.649 | 1.611 | 1.641 | |
| 0.6 | 1.822 | 1.772 | 1.810 | |
| 0.7 | 2.014 | 1.949 | 1.996 | |
| 0.8 | 2.226 | 2.144 | 2.201 | |
| 0.9 | 2.460 | 2.358 | 2.426 | |
| 1.0 | 2.718 | 2.594 | 2.673 |
Метод Эйлера и «улучшенный» метод, который, кстати, в литературе носит название метода Хьюна, несмотря на различия имеют много общего. И тот и другой метод можно представить в виде

В методе Эйлера:


Оба метода для получения очередного значения искомой функции требуют информации только об одной предыдущей точке. Такие методы называются одношаговыми или методами Рунге-Кутты. Для этих методов разработана теория, позволяющая получать с помощью формулы Тейлора методы любого порядка точности.
Использование метода высокого порядка позволяет добиться повышения точности и, следовательно, позволяет снизить необходимое число шагов интегрирования. Однако при этом усложняется вид 

Представление о многошаговых методах
Одношаговые методы никак не используют информацию о предыдущих шагах – предыстории решения. Для получения решения задачи Коши:

в точке 


Проинтегрируем дифференциальное уравнение (22.1) на отрезке 

Поскольку решение 


Здесь рассмотрим самый простой вариант, когда в качестве 


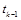



где 
Подставляя эту функцию в интеграл (22.2), получаем

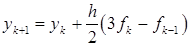
Выражение (22.5) описывает двухшаговый метод численного решения дифференциальных уравнений. Можно показать (см. [17.1]), что это метод второго порядка.
Используя значения 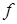

Очевидно формулы для многошаговых методов попроще, чем для одношаговых методов того же порядка. Однако у многошаговых методов есть и существенный недостаток – они не могут стартовать самостоятельно. Поэтому на практике обычно используется комбинированный подход. Сначала интегрирование ведется по методу Рунге-Кутты. Затем, когда уже пройдено достаточное количество шагов интегрирования, включается многошаговый метод.
ЗАКЛЮЧЕНИЕ
Данное пособие нельзя считать достаточно полным для детального изучения численных методов. Так, почти полностью опущены вопросы анализа погрешностей, доказательства сходимости. При обосновании методов предпочтение часто отдавалось не строгим математическим доказательствам, а геометрическим аналогиям, рассуждениям на «пальцах».
То есть надо отдавать себе отчет, что материал данного пособия предназначен лишь для предварительного знакомства с численными методами. Впрочем, воспользовавшись приведенными здесь описаниями алгоритмов, можно составить вполне корректные и работоспособные программы. Однако если вам придется заняться такой работой, очень скоро вы обнаружите, что для повышения быстродействия, точности результатов ваших программ понадобятся более полные сведения, которые можно найти, например, в литературе из списка в конце книги.
Еще немного о том, что стоит сохранить в своей памяти учащимся и зачем им это нужно. В самом деле, даже если по окончании института вы будете работать по специальности, то для расчетов вы будете чаще всего пользоваться не своими программами, а мощными программными комплексами типа NASTRAN, ДИАНА и др. Эти комплексы уже содержат программные средства для решения рассмотренных здесь задач. Так стоит ли тратить время на изучение всех этих численных методов, если можно будет воспользоваться готовыми программами? На взгляд автора, стоит и вот почему.
Во-первых, представление об этих методах необходимо хотя бы для того, чтобы можно было грамотно выбрать подходящий метод из предлагаемых вам конкретным программным комплексом. Так, для решения задачи о собственных значениях комплекс NASTRAN предлагает семь различных методов.
Во-вторых, стандартные программы, как правило, содержат специальные параметры, позволяющие управлять режимом работы программы. Чтобы более-менее обоснованно выбрать нужные значения таких параметров, необходимо хотя бы в общих чертах представлять себе, как работает данный метод, как он «устроен внутри».
В-третьих, первая же неприятность с использованием стандартных программ может поставить вас в положение автолюбителя, с тоской взирающего на остановившуюся машину и не представляющего, как сдвинуть ее с места. Для специалиста такая роскошь недопустима.
В-четвертых, при решении конкретных задач (например, расчет колебаний некоторой типовой конструкции) могут возникать достаточно специфические задачи с матрицами вполне определенной структуры. В таких случаях кустарные программы, учитывающие специфику конкретной задачи, могут оказаться эффективней профессионально выполненных стандартных программ, рассчитанных на общий случай.
Литература
17.1. Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989. – 432с.
http://astro.tsu.ru/OsChMet/11_3.html
http://lektsii.org/11-98535.html