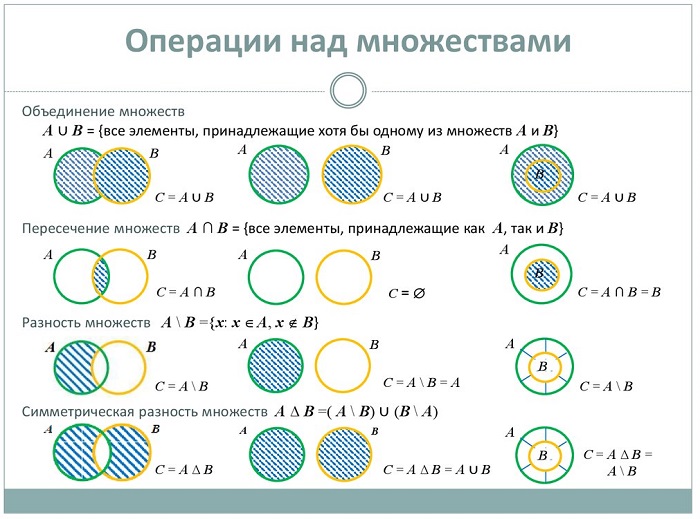
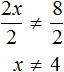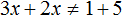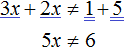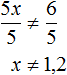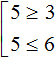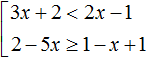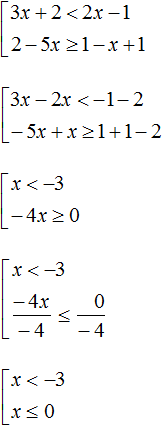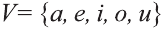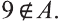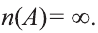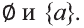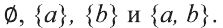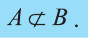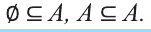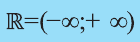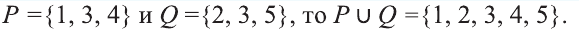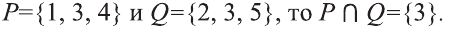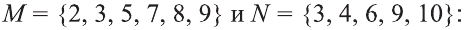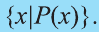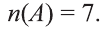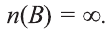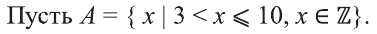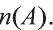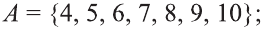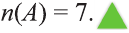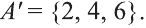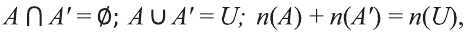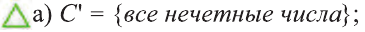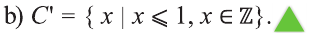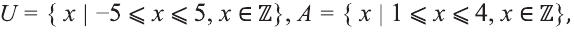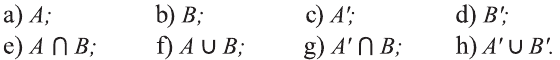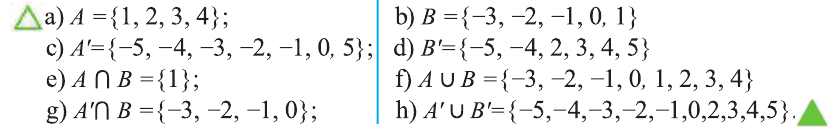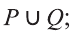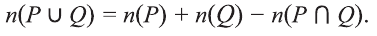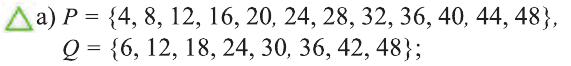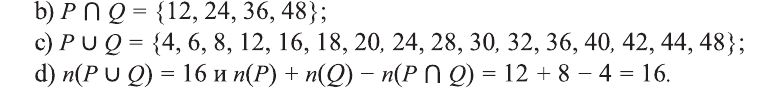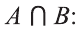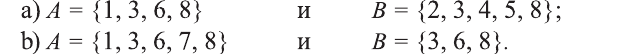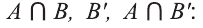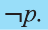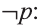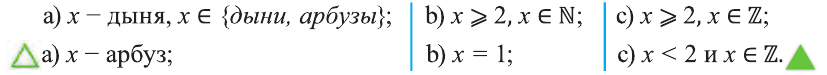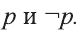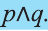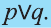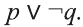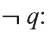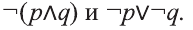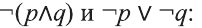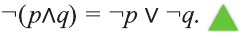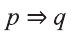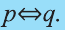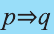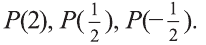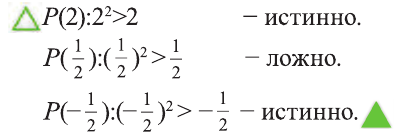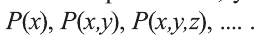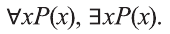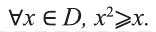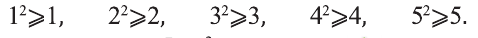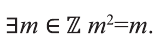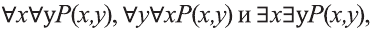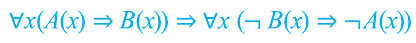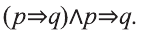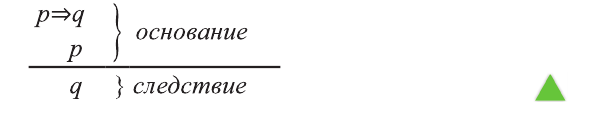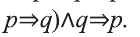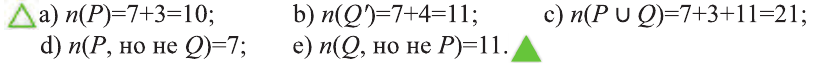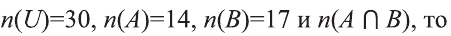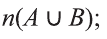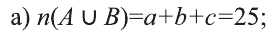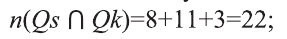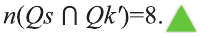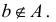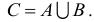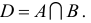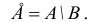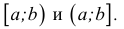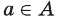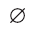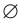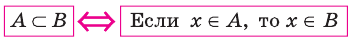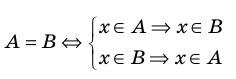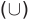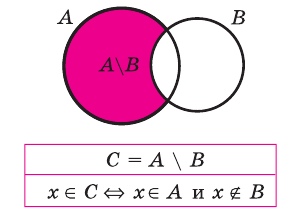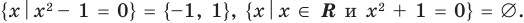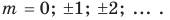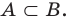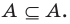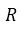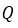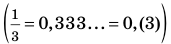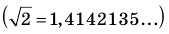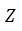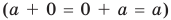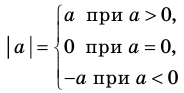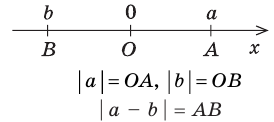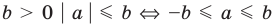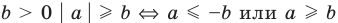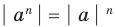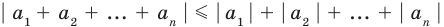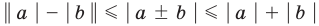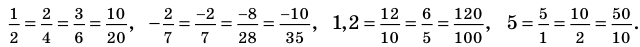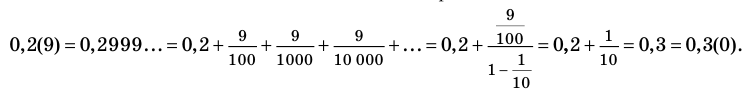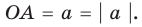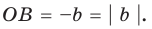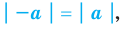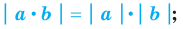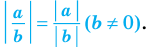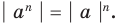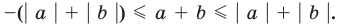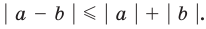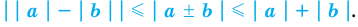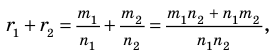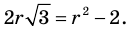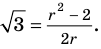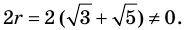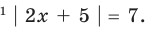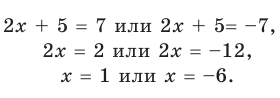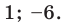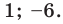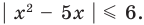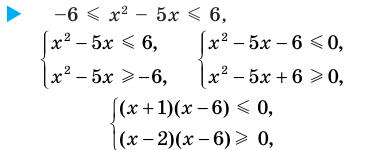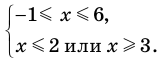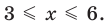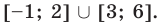Операции над множествами
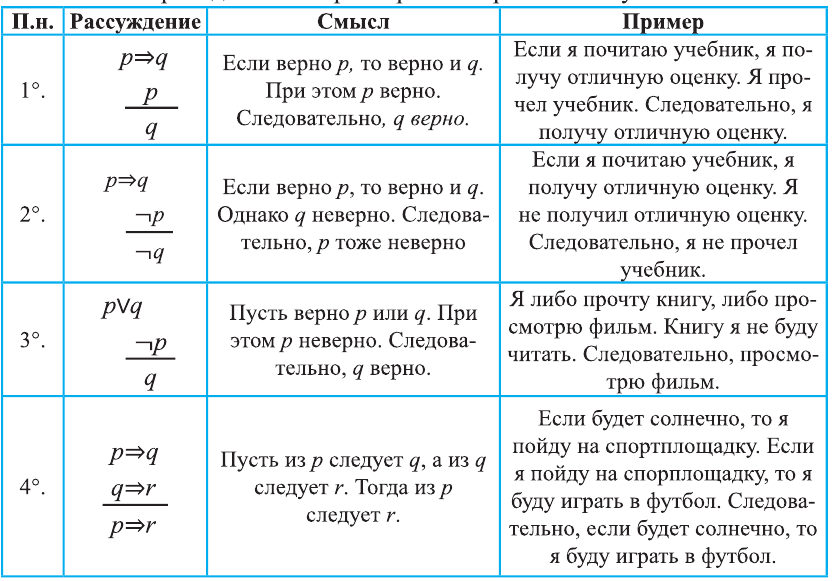
Пересечение множеств
Рассмотрим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Видим, что Том и Фред одновременно являются друзьями Джона и Майкла.
Говоря на языке множеств, элементы Том и Фред принадлежат как множеству друзей Джона, так и множеству друзей Майкла.
Зададим новое множество с названием «Общие друзья Джона и Майкла» и в качестве элементов добавим в него Тома и Фреда :
| Общие друзья Джона и Майкла | = |
В данном случае множество «Общие друзья Джона и Майкла» является пересечением множеств друзей Джона и Майкла.
Пересечением двух (или нескольких) исходных множеств называется множество, которое состоит из элементов, принадлежащих каждому из исходных множеств.
В нашем случае элементы Том и Фред принадлежат каждому из исходных множеств, а именно: множеству друзей Джона и множеству друзей Майкла.
Обозначим множество друзей Джона через букву A , множество друзей Майкла — через букву B , а множество общих друзей Джона и Майкла обозначим через букву C :
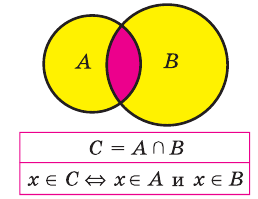
Тогда пересечением множеств A и B будет множество C и записываться следующим образом:
Символ ∩ означает пересечение.
Говоря о множестве, обычно подразумевают элементы, принадлежащие этому множеству. Символ пересечения ∩ читается, как союз И. Тогда выражение A ∩ B = C можно прочитать следующим образом:
«Элементы, принадлежащие множеству A И множеству B, есть элементы, принадлежащие множеству C».
«Друзья, одновременно принадлежащие Джону И Майклу, есть общие друзья Джона и Майкла».
Теперь представим, что у Джона и Майкла нет общих друзей. Для удобства, как и прежде обозначим множество друзей Джона через букву A , а множество друзей Майкла через букву B
В этом случае говорят, что исходные множества не имеют общих элементов и пересечением таких множеств является пустое множество. Пустое множество обозначается символом ∅
Пример 2. Рассмотрим два множества: множество A , состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Множество С является пересечением множеств A и B , поскольку элементы множества C одновременно принадлежат множеству A и множеству B
Пример 3. Рассмотрим два множества: множество A, состоящее из чисел 1, 5, 7, 9 и множество B , состоящее из чисел 1, 4, 5, 7
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Множество С является пересечением множеств A и B , поскольку элементы множества C одновременно принадлежат множеству A и множеству B.
Пример 4. Найти пересечение следующих множеств:
Пересечением множеств A , B и C будет множество, состоящее из элементов, принадлежащих каждому из множеств A , B и C . Этими элементами являются числа 3 и 9.
Зададим новое множество D и добавим в него элементы 3 и 9. Затем с помощью символа пересечения ∩ запишем, что пересечением множеств A, B и C является множество D
Чтобы найти пересечение, вовсе необязательно задавать множества с помощью букв. Если элементов мало, то множество можно задать прямым перечислением элементов.
К примеру, пусть первое множество состоит из элементов 1, 3, 5, а второе из элементов 2, 3, 5 . Пересечением в данном случае является множество, состоящее из элементов 3 и 5 . Чтобы записать пересечение, можно воспользоваться прямым перечислением:
Числовые промежутки, которые мы рассмотрели в предыдущих уроках, тоже являются множествами. Элементами таких множеств являются числа, входящие в числовой промежуток.
Например, отрезок [2; 6] можно понимать, как множество всех чисел от 2 до 6. Для наглядности можно перечислить все целые числа, принадлежащие данному отрезку:
Следует иметь ввиду, что мы перечислили только целые числа. Отрезку [2; 6] также принадлежат и другие числа, не являющиеся целыми, например, десятичные дроби. Десятичные дроби располагаются между целыми числами, но их количество настолько велико, что перечислить их не представляется возможным.
Еще пример. Интервал (2; 6) можно понимать, как множество всех чисел от 2 до 6, кроме чисел 2 и 6. Ранее мы говорили, что интервал это такой числовой промежуток, границы которого не принадлежат ему. Для наглядности можно перечислить все целые числа, принадлежащие интервалу (2; 6) :
Поскольку числовые промежутки являются множествами, то мы можем находить пересечения между различными числовыми промежутками. Рассмотрим несколько примеров.
Пример 5. Даны два числовых промежутка: [2; 6] и [4; 8] . Найти их пересечение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [2; 6] и [4; 8] :
Видно, что числа 4, 5, 6 принадлежат как первому промежутку [2; 6] , так и второму [4; 8] .
Тогда пересечением числовых промежутков [2; 6] и [4; 8] будет числовой промежуток [4; 6]
Изобразим промежутки [2; 6] и [4; 8] на координатной прямой. На верхней области отметим числовой промежуток [2; 6] , на нижней — промежуток [4; 8]
Видно, что числа, принадлежащие промежутку [4; 6] , принадлежат как промежутку [2; 6] , так и промежутку [4; 8] . Можно также заметить, что штрихи, входящие в промежутки [2; 6] и [4; 8] пересекаются в промежутке [4; 6] . В такой ситуации, когда перед глазами есть координатная прямая, понятие пересечения множеств можно понимать в прямом смысле, что очень удобно.
Пример 6. Найти пересечение числовых промежутков [−2; 3] и [4; 7]
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [−2; 3] и [4; 7] :
−2, −1, 0, 1, 2, 3 ∈ [−2; 3]
Видно, что числовые промежутки [−2; 3] и [4; 7] не имеют общих чисел. Поэтому их пересечением будет пустое множество:
Если изобразить числовые промежутки [−2; 3] и [4; 7] на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Пример 7. Дано множество из одного элемента < 2 >. Найти его пересечение с промежутком (−3; 4)
Множество, состоящее из одного элемента < 2 >, на координатной прямой изображается в виде закрашенного кружка, а числовой промежуток (−3; 4) это интервал, границы которого не принадлежат ему. Значит границы −3 и 4 будут изображаться в виде пустых кружков:
Пересечением множества < 2 >и числового промежутка (−3; 4) будет множество, состоящее из одного элемента < 2 >, поскольку элемент 2 принадлежит как множеству < 2 >, так и числовому промежутку (−3; 4)
На самом деле мы уже занимались пересечением числовых промежутков, когда решали системы линейных неравенств. Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
По сути, множество решений, удовлетворяющих обоим неравенствам, является пересечением множеств решений первого и второго неравенства. Роль этих множеств берут на себя числовые промежутки.
Например, чтобы решить систему неравенств 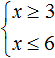
В данном примере решением первого неравенства x ≥ 3 является множество всех чисел, которые больше 3 (включая само число 3). Иначе говоря, решением неравенства является числовой промежуток [3; +∞)
Решением второго неравенства x ≤ 6 является множество всех чисел, которые меньше 6 (включая само число 6). Иначе говоря, решением неравенства является числовой промежуток (−∞; 6]
А общим решением системы будет пересечение множеств решений первого и второго неравенства, то есть пересечение числовых промежутков [3; +∞) и (−∞; 6]
Если мы изобразим множество решений системы 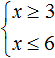
Поэтому в качестве ответа мы указывали, что значения переменной x принадлежат числовому промежутку [3; 6], то есть пересечению множеств решений первого и второго неравенства
Пример 2. Решить неравенство
Все неравенства, входящие в систему уже решены. Нужно только указать те решения, которые являются общими для всех неравенств.
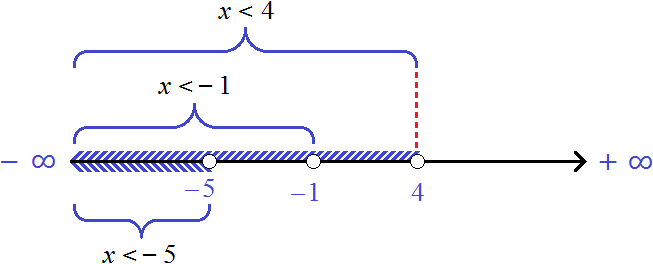
Решением первого неравенства является числовой промежуток (−∞; −1) .
Решением второго неравенства является числовой промежуток (−∞; −5) .
Решением третьего неравенства является числовой промежуток (−∞; 4) .
Решением системы 
На рисунке представлены числовые промежутки и неравенства, которыми эти числовые промежутки заданы. Видно, что числа, принадлежащие промежутку (−∞; −5) , одновременно принадлежат всем исходным промежуткам.
Запишем ответ к системе 
Пример 3. Решить неравенство
Решением первого неравенства y > 7 является числовой промежуток (7; +∞) .
Решением второго неравенства y является числовой промежуток (−∞; 4) .
Решением системы 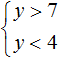
В данном случае пересечением числовых промежутков (7; +∞) и (−∞; 4) является пустое множество, поскольку эти числовые промежутки не имеют общих элементов:
Если изобразить числовые промежутки (7; +∞) и (−∞; 4) на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Объединение множеств
Объединением двух (или нескольких) исходных множеств называют множество, которое состоит из элементов, принадлежащих хотя бы одному из исходных множеств.
На практике объединение множеств состоит из всех элементов, принадлежащих исходным множествам. Поэтому и говорят, что элементы такого множества принадлежат хотя бы одному из исходных множеств.
Рассмотрим множество A с элементами 1, 2, 3 и множество B с элементами 4, 5, 6.
Зададим новое множество C и добавим в него все элементы множества A и все элементы множества B
В данном случае объединением множеств A и B является множество C и обозначается следующим образом:
Символ ∪ означает объединение и заменяет собой союз ИЛИ. Тогда выражение A ∪ B = C можно прочитать так:
Элементы, принадлежащие множеству A ИЛИ множеству B, есть элементы, принадлежащие множеству C.
В определении объединения сказано, что элементы такого множества принадлежат хотя бы одному из исходных множеств. Данную фразу можно понимать в прямом смысле.
Вернёмся к созданному нами множеству C , куда входят все элементы множеств A и B . Возьмём для примера из этого множества элемент 5. Что можно про него сказать?
Если 5 является элементом множества C , а множество С является объединением множеств A и B , то можно с уверенностью заявить, что элемент 5 принадлежит хотя бы одному из множеств A и B . Так оно и есть:
Возьмем ещё один элемент из множества С , например, элемент 2. Что можно про него сказать?
Если 2 является элементом множества C , а множество С является объединением множеств A и B , то можно с уверенностью заявить, что элемент 2 принадлежит хотя бы одному из множеств A и B . Так оно и есть:
Если мы захотим объединить два или более множества и вдруг обнаружим, что один или несколько элементов принадлежат каждому из этих множеств, то в объединение повторяющиеся элементы будут входить только один раз.
Например, рассмотрим множество A с элементами 1, 2, 3, 4 и множество B с элементами 2, 4, 5, 6.
Видим, что элементы 2 и 4 одновременно принадлежат и множеству A , и множеству B . Если мы захотим объединить множества A и B , то новое множество C будет содержать элементы 2 и 4 только один раз. Выглядеть это будет так:
Чтобы при объединении не допустить ошибок, обычно поступают так: сначала в новое множество добавляют все элементы первого множества, затем добавляют элементы второго множества, которые не принадлежат первому множеству. Попробуем сделать такое объединение с множествами A и B .
Итак, у нас имеются следующие исходные множества:
Зададим новое множество С и добавим в него все элементы множества A
Теперь добавим элементы из множества B , которые не принадлежат множеству A . Множеству A не принадлежат элементы 5 и 6 . Их и добавим во множество C
Пример 2. Друзьями Джона являются Том, Фред, Макс и Джордж. А друзьями Майкла являются Лео, Том, Фред и Эван. Найти объединение множеств друзей Джона и Майкла.
Для начала зададим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Зададим новое множество с названием «Все друзья Джона и Майкла» и добавим в него всех друзей Джона и Майкла.
Заметим, что Том и Фред одновременно являются друзьями Джона и Майкла, поэтому мы добавим их в новое множество только один раз, поскольку сразу двух Томов и двух Фредов не бывает.
| Все друзья Джона и Майкла | = |
В данном случае множество всех друзей Джона и Майкла является объединением множеств друзей Джона и Майкла.
Друзья Джона ∪ Друзья Майкла = Все друзья Джона и Майкла
Пример 3. Даны два числовых промежутка: [−7; 0] и [−3; 5] . Найти их объединение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие этим промежуткам:
−7, −6, −5, −4, −3,−2, −1 , 0 ∈ [−7; 0]
−3,−2, −1 , 0, 1, 2, 3, 4, 5 ∈ [−3; 5]
Объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5] , который содержит все числа промежутка [−7; 0] и [−3; 5] без повторов некоторых из чисел
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Обратите внимание, что числа −3,−2, −1 принадлежали и первому промежутку и второму. Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Значит объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5]
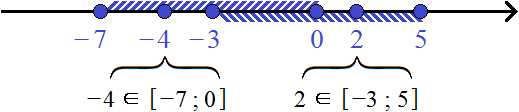
Изобразим на координатной прямой промежутки [−7; 0] и [−3; 5] . На верхней области отметим числовой промежуток [−7; 0] , на нижней — промежуток [−3; 5]
Ранее мы выяснили, что промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5] . Здесь полезно вспомнить про определение объединения множеств, которое было приведено в самом начале. Объединение трактуется, как множество, состоящее из всех элементов, принадлежащих хотя бы одному из исходных множеств.
Действительно, если взять любое число из промежутка [−7; 5] , то окажется, что оно принадлежит хотя бы одному из промежутков: либо промежутку [−7; 0] либо промежутку [−3; 5] .
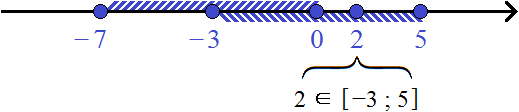
Возьмём из промежутка [−7; 5] любое число, например число 2 . Поскольку промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5] , то число 2 будет принадлежать хотя бы одному из этих промежутков. В данном случае число 2 принадлежит промежутку [−3; 5]
Возьмём ещё какое-нибудь число. Например, число −4 . Это число будет принадлежать хотя бы одному из промежутков: [−7; 0] или [−3; 5] . В данном случае оно принадлежит промежутку [−7; 0]
Возьмём ещё какое-нибудь число. Например, число −2 . Оно принадлежит как промежутку [−7; 0] , так и промежутку [−3; 5] . Но на координатной прямой оно указывается только один раз, поскольку в одной точке сразу два числа −2 не бывает.
Не каждое объединение числовых промежутков является числовым промежутком. Например, попробуем найти объединение числовых промежутков [−2 ; −1] и [4 ; 7].
Идея остаётся та же самая — объединением числовых промежутков [−2 ;−1] и [4 ; 7] будет множество, состоящее из элементов, принадлежащих хотя бы одному из промежутков: [−2; −1] или [4; 7] . Но это множество не будет являться числовым промежутком. Для наглядности перечислим все целые числа, принадлежащие этому объединению:
Получили множество < −2, −1, 4, 5, 6, 7 >. Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4 , не вошли в полученное множество
Числовой промежуток должен содержать все числа от левой границы до правой. Если одно из чисел отсутствует, то числовой промежуток теряет смысл. Допустим, имеется линейка длиной 15 см
Эта линейка является числовым промежутком [0; 15], поскольку содержит все числа в промежутке от 0 до 15 включительно. Теперь представим, что на линейке после числа 9 сразу следует число 12.
Эта линейка не является линейкой в 15 см, и её нежелательно использовать для измерения. Также, её нельзя назвать числовым промежутком [0; 15] , поскольку она не содержит все числа, которые должна была содержать.
Решение неравенств, содержащих знак ≠
Некоторые неравенства содержат знак ≠ (не равно). Например, 2x ≠ 8 . Чтобы решить такое неравенство, нужно найти множество значений переменной x , при которых левая часть не равна правой части.
Решим неравенство 2x ≠ 8 . Разделим обе части данного неравенства на 2, тогда получим:
Получили равносильное неравенство x ≠ 4 . Решением этого неравенства является множество всех чисел, не равных 4. То есть если мы подставим в неравенство x ≠ 4 любое число, которое не равно 4, то получим верное неравенство.
Подставим, например, число 5
5 ≠ 4 — верное неравенство, поскольку 5 не равно 4
7 ≠ 4 — верное неравенство, поскольку 7 не равно 4
И поскольку неравенство x ≠ 4 равносильно исходному неравенству 2x ≠ 8 , то решения неравенства x ≠ 4 будут подходить и к неравенству 2x ≠ 8 . Подставим те же тестовые значения 5 и 7 в неравенство 2x ≠ 8 .
Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:
Теперь запишем ответ в виде числового промежутка. Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞) . Напомним, что для слова «или» используется символ ∪
В этом выражении говорится, что значения, принимаемые переменной x , принадлежат промежутку (−∞; 4) или промежутку (4; +∞).
Неравенства, содержащие знак ≠ , также можно решать, как обычные уравнения. Для этого знак ≠ заменяют на знак = . Тогда получится обычное уравнение. В конце решения найденное значение переменной x нужно исключить из множества решений.
Решим предыдущее неравенство 2x ≠ 8 , как обычное уравнение. Заменим знак ≠ на знак равенства = , получим уравнение 2x = 8 . Разделим обе части данного уравнения на 2 , получим x = 4 .
Видим, что при x , равном 4, уравнение обращается в верное числовое равенство. При других значениях равенства соблюдаться не будет. Эти другие значения нас и интересуют. А для этого достаточно исключить найденную четвёрку из множества решений.
Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x
Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 5
Решением неравенства x ≠ 1,2 является множество всех чисел, не равных 1,2 .
Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:
В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)
Решение совокупностей неравенств
Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.
А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.
Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:
Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.
Решением первого неравенства x ≥ 3 является числовой промежуток [3; +∞) . Решением второго неравенства x ≤ 6 является числовой промежуток (−∞; 6] .
Множество значений x , при которых верно хотя бы одно из неравенств, будет принадлежать промежутку [3; +∞) или промежутку (−∞; 6] . Так и записываем:
В этом выражении говорится, что переменная x , входящая в
совокупность 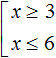
Например, число 9 из промежутка [3; +∞) удовлетворяет первому неравенству x ≥ 3. А число −7 из промежутка (−∞; 6] удовлетворяет второму неравенству x ≤ 6.
Посмотрите внимательно на выражение x ∈ [3; +∞) ∪ (−∞; 6], а именно на его правую часть. Ведь выражение [3; +∞) ∪ (−∞; 6] представляет собой объединение числовых промежутков [3; +∞) и (−∞; 6] . Точнее, объединение множеств решений первого и второго неравенства.
Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности 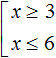
Объединением числовых промежутков [3; +∞) и (−∞; 6] является промежуток (−∞; +∞) . Точнее, объединением числовых промежутков [3; +∞) и (−∞; 6] является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.
Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.
Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6
Возьмем еще какое-нибудь число, например, число 5 . Оно удовлетворяет и первому неравенству x ≥ 3 и второму x ≤ 6
Пример 2. Решить совокупность неравенств
Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.
Для начала найдём множество решений первого неравенства x . Этим множеством является числовой промежуток (−∞; −0,25) .
Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).
Решением совокупности неравенств 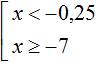
Иначе говоря, решением совокупности 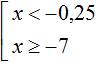
Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Пример 3. Решить совокупность неравенств
Решим каждое неравенство по отдельности:
Множеством решений первого неравенства x является числовой промежуток (−∞; −3) .
Множеством решений второго неравенства x ≤ 0 является числовой промежуток (−∞; 0] .
Решением совокупности неравенств 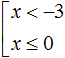
Иначе говоря, решением совокупности 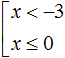
Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]
Ответ можно оставить таким, каким мы его записали ранее:
Множества — определение и вычисление с примерами решения
Содержание:
Множества
Понятие множества является одним из исходных понятий математики в том смысле, что его нельзя определить с помощью более простых, чем оно само, понятий. В повседневной жизни часто приходится рассматривать набор некоторых объектов как единое целое. Скажем, когда биолог изучает флору и фауну некоторой местности, он делит организмы на виды, а виды на семейства. При этом каждый вид рассматривается как единое целое, состоящее из организмов.
Множество может состоять из объектов различной природы. Например, вес реки Азии или все слова в словаре могут рассматриваться как множества.
Знаменитый немецкий математик Г. Кантор (1845 -1918) дал следующую описательную формулировку: «Множество есть совокупность, мыслимая как единое целое».
Объекты, составляющие множество, называются его элементами.
Обычно, для удобства, множество обозначается заглавными буквами латинского алфавита, например, А, В, С. а его элементы — прописными.
Множество А, состоящее из элементов а, b, с, . , будем записывать в виде A = <а, b, с. >. Отметим, что записи <6, 11>, <11, 6>, <11, 6, 6, 11>означают одно и то же множество.
При ведем примеры множеств. Например, множество <0, 1, 2, 3, 4, 5, 6, 7, 8, 9>— множество цифр десятичной системы счисления ,
То, что х является элементом множества А, будем обозначать как 
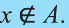
Например, для множества 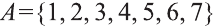

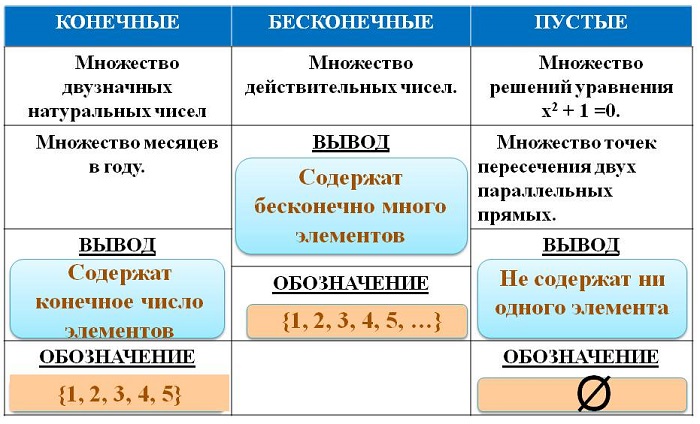
Если число элементов, составляющих множество, конечно, то такое множество будем называть конечным, в противном случае бесконечным. Например, множество 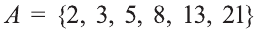
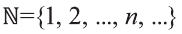
В качестве еще одного примера бесконечного множества можно привести множество всех натуральных чисел, не меньших 13.
Обозначим через 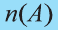
в силу того, что число всех его элементов равно 6. Множество, не содержащее ни одного элемента, называется пустым и обозначается так: 0
Пустое множество 0 считается конечным и для него я(0)= 0.
Для бесконечного множества А принято, что
Если вес элементы множества А также принадлежат множеству В, то говорят, что множество А — подмножество множества В и обозначают так: 
Во множестве <а>лежат два подмножества:
Множество <а, b>имеет четыре подмножества:
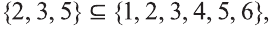
Если множество А имеет элементы, не принадлежащие В, то множество А не может быть подмножеством В. Этот факт мы будем записывать так:
Например, пусть А=< 1, 2, 3, 4>, В=<2, 3, 4, 5>. Так как 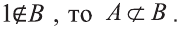
Если 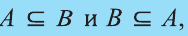
Например, множество всех правильных треугольников совпадает со множеством всевозможных треугольников, у которых все углы равны. Причина этого заключается в том, что у любого правильного треугольника
все углы равны, и, наоборот, если у треугольника все углы равны, то он является правильным.
Напомним основные числовые множества: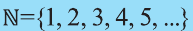
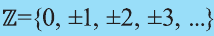
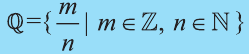
Множество действительных чисел
Объединение и пересечение множеств
1) Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А, В, называется объединением множеств.
Объединение множеств А, В обозначается через
Например, если
2) Множество, состоящее из элементов, принадлежащих обоим множествам А, В, называется пересечением множеств. Пересечение множеств А. В обозначается через
Например, если
Множества, не имеющие общих элементов, называются не пересекающимися.
Пример:
Для множеств
a) определите, какие из утверждений верны, а какие неверны:
b) найдите множества:
c) определите, какие из утверждений верны, а какие неверны:
Решение:
а) Так как число 4 не является элементом множества М, то утверждение 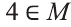
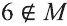
b). 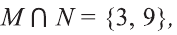
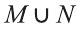
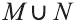
c) Утверждение 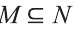
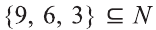
В некоторых случаях для задания множества указывается характеристическое свойство, истинное для всех элементов множества и ложное для остальных. Если мы кратко запишем тот факт, что элемент х удовлетворяет свойству Р как Р(х), то множество всех элементов, удовлетворяющих свойству Р обозначается так:
Например, запись 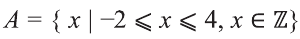
На числовом луче это множество изображается так:
Видно, что 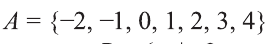
Аналогично запись 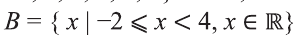
На числовом луче это множество изображается так:
Видно, что, 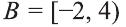
Пример:
a) Как читается эта запись?
b) Выпишите последовательно элементы этого множества.
c) Найдите
Решение:
a) «Множество всех целых чисел, больших 3 и меньших или равных 10»;
b).
c).
Рассмотрим множество всех натуральных чисел, больших или равных 1, но меньших или равных 8. Пусть нас интересуют только его подмножества.
В таком случае, обычно вводится множество 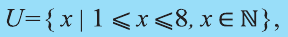
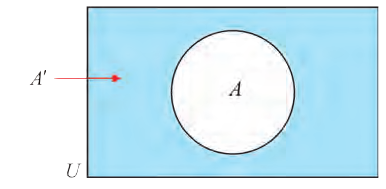
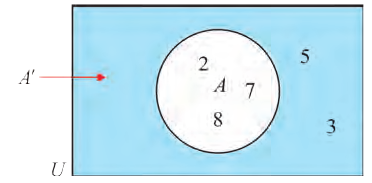
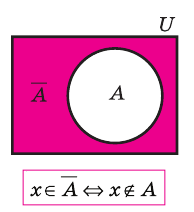
Множество А\ содержащее все элементы универсального множества U, не являющиеся элементами множества А, называется дополнением множества А.
Например, если 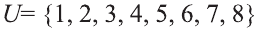
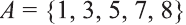
Очевидно, что
т.е. множества А и А’ не имеют общих элементов, а также вес составляющие их элементы образуют в совокупности универсальное множество U.
Пример:
Пусть U универсальное множество. Найдите С’, если:
Решение:
Пример:
Пусть
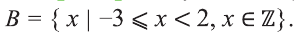
Решение:
Пример:
Пусть 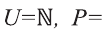
b) найдите 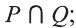
d) проверьте выполнение равенства
Решение:
Значит, 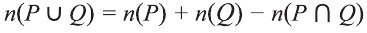
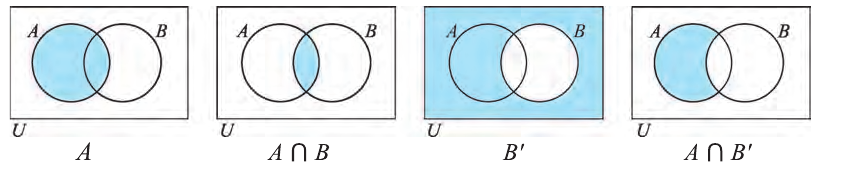
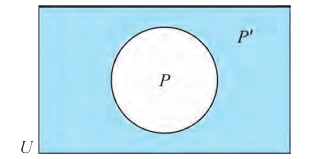
Диаграммы Венна
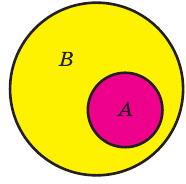
Например, на этом рисунке изображено множество А, лежащее внутри универсального множества 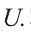
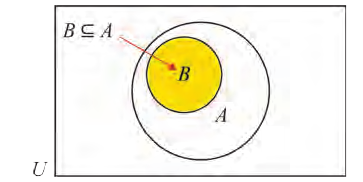
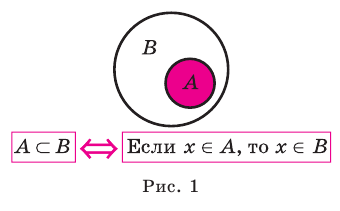
Если 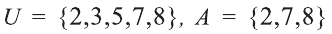
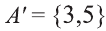
Мы знаем, что если 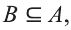
Все элементы пересечения 
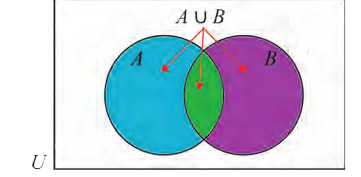
Все элементы объединения A U В принадлежат либо А, либо В, либо обоим одновременно. Значит, на соответствующей диаграмме Венна область, соответствующая множеству A U В, изображается следующим образом:
Пример:
Пусть 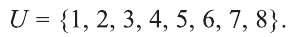
Решение:
Удобно на диаграмме Венна множества раскрашивать.
Например, на рисунке раскрашены множества А,
Высказывание
Высказывание — это повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Вопросительные предложения, повествовательные предложения, описывающие личное отношение субъекта, например «Зеленый цвет приятен», не являются высказываниями. Отметим, что существуют высказывания, истинность или ложность которых не определяются однозначно.
Например, высказывание «Этот писатель родился в Ташкенте» может быть истинным по отношению к некоторым писателям и ложным по отношению к другим.
Пример:
Укажите, какие из предложений являются высказываниями. В случае, когда предложение является высказыванием, однозначно ли определяется его истинность — ложность?
а) 20:4=80; b) 25-8=200;
с) Где мой карандаш? d) У тебя глаза голубые.
Решение:
a) Это высказывание и оно ложно, так как 20:4=5;
b) это высказывание и оно истинно;
c) это вопросительное предложение и поэтому оно не является высказыванием;
d) это высказывание. Истинность-ложность его определяется неоднозначно, так как применительно к некоторым людям оно истинно, а к другим — ложно.
Мы будем обозначать высказывания буквами p,q,r . .
Например, р: во вторник прошел дождь; q: 20:4=5; r: х — четное число. Для построения нескольких сложных высказываний служат символы, называемые логическими связками: 


Рассмотрим их подробней.
Отрицание
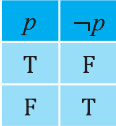
Для высказывания р высказывание вида «не р» или «неверно, что р» называется отрицанием высказывания р и обозначается как
р: Во вторник шел дождь
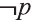
р: У Мадины глаза голубые
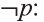
Ясно, что если р истинно, то 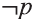
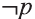
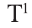
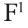
1 Буквы Т и F — начальные буквы английских слов «true» (истинно) и «false» (ложно) соответственно.
Пример:
Составьте отрицание высказывания:
Решение:
Удобно находить отрицание высказывания с помощью диаграмм Венна. Например, рассмотрим высказывание:
р: «Число х больше, чем 10 «.
На диаграмме U — множество всех чисел, множество Р — множество истинности высказывания р, то есть множество всех х , для которых это высказывание истинно. Множество Р’ является множеством истинности отрицания 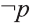
Пример:
На множестве 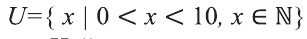
Решение:
Пусть множество Р — множество истинности высказывания р, а множество Р’ — множество высказывания 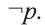
Конъюнкция
Высказывание, образованное из двух высказываний с помощью связки «и», называется конъюнкцией заданных высказываний.
Конъюнкция высказываний р, q обозначается через
Например, конъюнкция высказываний,
р: Эльдар на завтрак ел плов;
q: Эльдар на завтрак ел самсу.
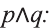
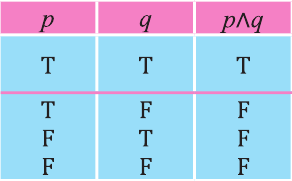
Видно, что высказывание 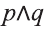
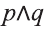
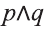
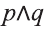
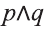
Первый и второй столбцы таблицы составлены из всех возможных значений истинности высказываний р, q.
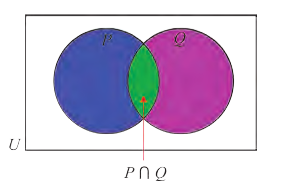
На диаграмме Р — множество истинности высказывания р, Q — множество истинности высказывания q , а множество истинности высказывания 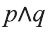
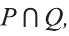
Дизъюнкция
Высказывание, образованное из двух высказываний с помощью связки «или», называется дизъюнкцией заданных высказываний.
Дизъюнкция высказываний р, q обозначается через
Например, дизъюнкция высказываний,
р: Эльдар сегодня посетит библиотеку,
q: Эльдар сегодня посетит театр .
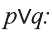
Высказывание 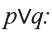
Высказывание 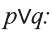
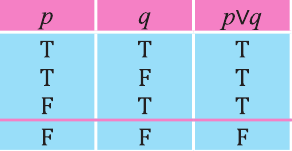
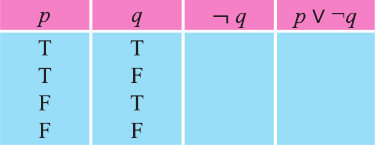
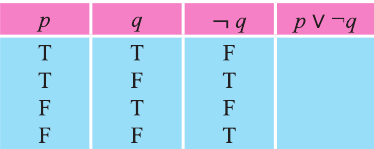
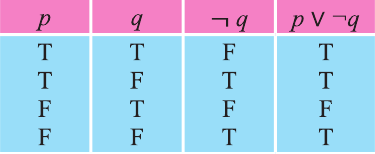
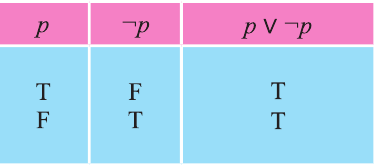
Дизъюнкция имеет следующую таблицу истинности:
pVq истинно, когда хотя бы одно из высказываний р, q истинно.
pVq ложно, когда оба высказывания p, q ложны.
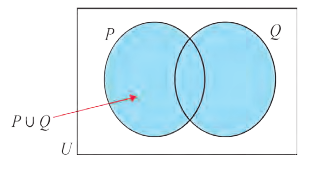
На диаграмме Р — множество истинности высказывания р, Q — множество истинности высказывания q, а множество истинности высказывания pVq является множество 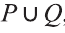
Логическая равносильность
Составим, используя буквы и символы логических связок таких, как отрицание, конъюнкция и дизъюнкция, символическую запись более сложных высказываний естественного языка, при этом не обращая внимания на их истинность или ложность.
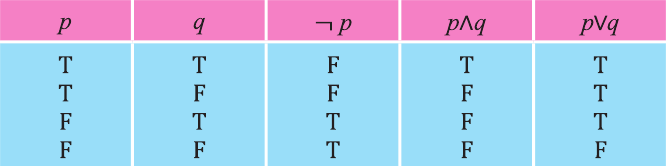
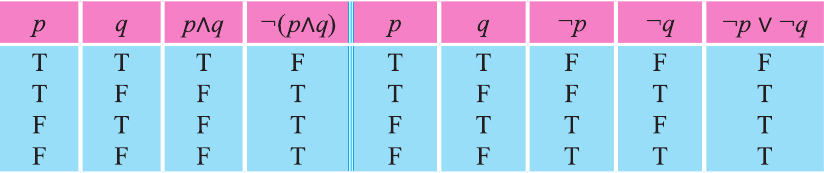
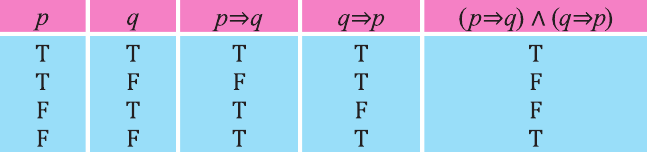
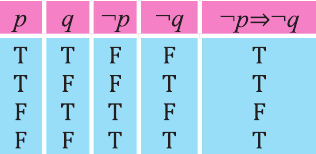
Объединяя таблицы истинности для отрицания, конъюнкции и дизъюнкции, можно составить таблицы истинности для более сложных высказываний:
Пример 1. Составьте таблицу истинности высказывания
1 шаг.
Выпишем таблицу и заполним сначала первый и второй столбец всеми возможными значениями истинности р и q:
2 шаг. Учитывая значения истинности q, заполним третий столбец значениями истинности
3 шаг Учитывая значения истинности p и 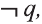
Высказывание, являющееся истинным всегда, называется законом логики или тавтологией.
То, что высказывание является законом логики, можно доказать при помощи таблицы истинности.
Пример:
Докажите, что высказывание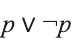
Заполним таблицу истинности:
Решение:
Видно, что высказывание 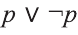
Если для двух высказываний соответствующие их значениям истинности столбцы одинаковы, то эти высказывания называются логически равносильными.
Пример:
Докажите, что следующие высказывания являются логически равносильными
Решение:
Составим таблицы истинности для высказываний
Так как у высказываний 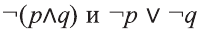
Мы будем обозначать этот факт так:
Импликация
Высказывание, образуемое из двух высказываний с помощью связки «если . то . » называется импликацией этих двух высказываний.
Импликация «Если р, то q» обозначается как 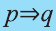
При этом высказывание р называется достаточным условием для q, а высказывание q — необходимым условием для р.
высказывание q — необходимым условием для р.
Рассмотрим , например, высказывания
р: У Сардора есть телевизор; q: Сардор будет смотреть кино.
Тогда высказывание 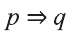
Если у Сардора есть телевизор, то он будет смотреть кино.
Точно также
Для того, чтобы Сардор смотрел кино достаточно, чтобы у него был телевизор.
Можно заметить, что высказывание 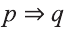
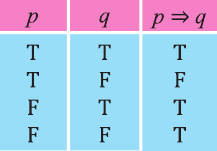
Пример:
р: «Анора часто смотрит кинофильмы»;
q: «Барно часто смотрит кинофильмы
r: «Барно не сдаст экзамен»;
s: «произойдет чудо».
Имеем: 1. 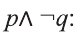
2. 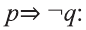
3. 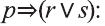
4. 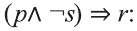
5. 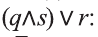
Эквиваленция
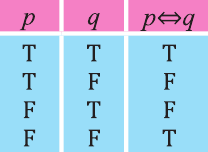
Высказывание вида 
Запись 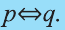
Пример:
р: х — четно, q: последняя цифра числа х четна. Выразите высказывание
Решение:
Рассмотрим высказывание,

Тогда запись 

Видно, что высказывание 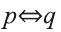
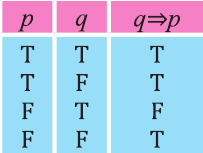
Конверсия
Конверсией высказывания 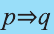
Конверсия имеет следующую таблицу истинности:
Пример:
р: треугольник равнобедренный,
q: два угла треугольника равны.
Выразите на естественном языке высказывание 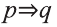
Решение:
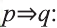
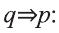
Инверсия
Инверсией высказывания 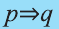
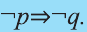
Эта таблица совпадает с таблицей истинности высказывания 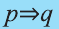
Контрапозиция
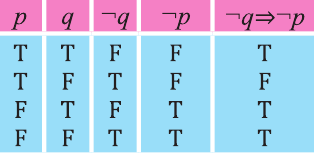
Контрапозицией высказывания 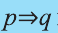

Эта таблица совпадает с таблицей истинности высказывания 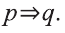
Пример:
Рассмотрим высказывание. Все учителя живут поблизости от школы». Составим его контрапозицию.
Решение:
Данное высказывание можно сформулировать так: «Если этот человек — учитель, что он живет поблизости от школы».
Это предложение имеет форму 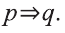
р: этот человек — учитель,
q: этот человек живет поблизости от школы.
Контрапозиция 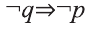
«Если этот человек не живет поблизости от школы, то он не является учителем.
Пример:
р: Самандар находится в библиотеке, q: Самандар читает книгу.
Составьте имликацию, конверсию, инверсию и контрапозицию
Решение:
Отметим, что импликация и конверсия логически не равносильны, так как , например , Самандар может читать книгу и в классе.
Предикаты и кванторы
В некоторых предложениях участвуют переменные, при этом подставив вместо них конкретные значения, получим высказывания. Такие предложения называются предикатами.
Пример:
Пусть задан предикат 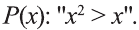
Решение:
В некоторых предикатах переменную можно определить исходя из контекста.
Например, в предложениях «Этот писатель родился в Ташкенте» и «Он родился в Ташкенте» переменными являются словосочетание». «Этот писатель» и местоимение «он» соответственно. Если вместо переменной подставить значение «Абдулла Кадыри», получим истинное высказывание «Абдулла Кадыри родился в Ташкенте». Если вместо переменной подставить значение «Шекспир», получим ложное высказывание «Шекспир родился в Ташкенте».
Обозначив переменную через х, вышеуказанные предложения можно записать в виде «х родился в Ташкенте».
В предикате могут участвовать одно или несколько переменных. В зависимости от количества переменных, участвующих в предикате, будем обозначать его так:
Используя совместно с предикатом специальные символы 
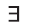
Например, новое высказывание вида 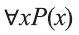
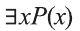
К примеру, рассмотрим предикат Р(х): «х родился в Самарканде». Тогда высказывание 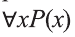
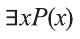
Приведем примеры, в которых можно определить истинность-ложность высказываний вида
Пример:
Пусть 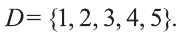
Решение:
Проверим:
Значит, высказывание, 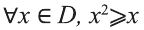
Следует отметить, что для того, чтобы доказать ложность высказывания 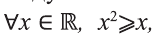
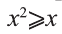
Действительно, при
Любое значениех, которое показывает, что высказывание 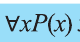
Пример:
Докажите истинность высказывания
Решение:
Так как 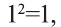
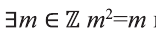
Если же 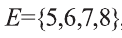
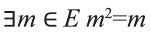
Приведем два важных закона логики, связанных с операцией отрицания:
Для понимания смысла этих законов приведем пример.
Если запись 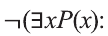
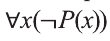
не существует отличников», тогда запись означает логически равносильное ему утверждение «Все мои одноклассники не являются отличниками».
Точно также, формула 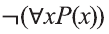
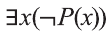
Очевидно, что с помощью кванторов и предиката 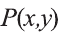
из которых, в свою очередь, можно построить всказывания вида:
В то время, когда смысл высказываний
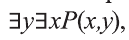
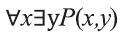
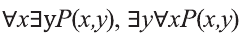
Рассмотрим, например, предикат Р(х,у): человек у — отец моего одноклассника х.
В этом случае 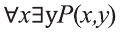
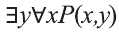
Аналогично можно показать, что высказывания,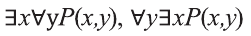
С помощью кванторов и предикатов можно построить и другие законы логики. Например, высказывание «Если все вороны черные, то ни одна не черная птица не является вороной «, служит примером закона логики вида:
Законы правильного мышления (аргументации)
В процессе познания действительности мы приобретаем новые знания. Некоторые из них непосредственно, в результате воздействия предметов внешнего мира на органы чувств. Но большую часть знаний мы получаем пу тем выведения новых знаний из знаний уже имеющихся. Чтобы научиться стройно и последовательно излагать свои мысли, правильно делать выводы, необходимо пользоваться законами логики. Определенность, непротиворечивость, последовательность и обоснованность являются обязательными качествами правильного мышления. Законы логики устанавливают необходимые связи в последовательном ряду мыслей и умозаключений.
Суждение представляет собой форму мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах или отношениях. Например, в суждении «Железо-металл» утверждается связь между предметом (железо) и его признаком (являться металлом). В суждении «Яйцо появилось раньше курицы » утверждается связь между двумя предметами (яйцо и курица). Так как суждение выражается в форме повествовательного предложения, причем суждение может быть либо истинным, либо ложным, то каждое суждение имеет форму высказывания.
Умозаключение- это такая форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам получается некоторое суждение, называемое заключением или выводом.
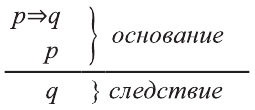
Пусть S-совокупность исходных суждений (посылок), Р- заключение. В этом случае, умозаключение имеет логическую форму вида 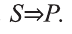
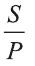
Если Собир занимается спортом, то будет здоров. Собир занимается спортом. Следовательно, Собир будет здоров.
Найдем логическую форму этого умозаключения.
Пусть р: Собир занимается спортом; q: Собир будет здоров. Тогда умозаключение имеет вид:
Так следствие вытекает из суждений 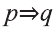
Составим соответствующую таблицу истинности:
Получили тавтологию. Это показывает правильность умозаключения, то есть мы из данного основания получили правильное следствие.
Пример:
Покажите неправильность умозаключения:
Если треугольник имеет три стороны, то 2+4-7.
Следовательно, треугольник имеет три стороны.
Решение:
Найдем логическую форму этого умозаключения.
р: треугольник имеет три стороны.
Так как здесь 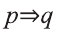
Составим соответствующую таблицу истинности:
В результате мы не получили тавтологию. Это показывает неверность умозаключения, то есть мы из данного основания не получили правильное следствие.
Ниже мы приведем некоторые правила правильных умозаключений:
Доказательство верности вышеуказанных умозаключений мы оставляем учащимся в качестве упражнения.
Софизмы и парадоксы
Одним из первых соответствующие примеры привел математик Зенон, живший в 5 веке до нашей эры в Древней Греции. Например, Зенон «доказал», что быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения она находится впереди Ахиллеса. Приведем его рассуждения. Допустим, Ахиллес бежит в 10 раз быстрее, чем черепаха, и находи тся позади нее на расстоянии в 100 шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползет 10 шагов.
За то время, за которое Ахиллес пробежит 10 шагов, черепаха проползет еще 1 шаг, и так далее. Процесс будет длиться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Примеры Зенона связаны с понятиями бесконечности и движения, которые имели большое значение в развитии физики и математики.
Некоторые софизмы обсуждали в переписке между собой наши великие соотечественники Беруни и Ибн Сино, а также они встречаются в произведениях Фараби.
Приведем простейшие примеры на софизмы и обсудим их.
Пример:
Куда пропали 1000 руб? Три друга отобедали в кафе, после чего официант дал им счет на 25000 руб. Каждый из трех друзей достал по купюре в 10000 руб, в итоге они отдали официанту 30000 руб. На сдачу официант отдал 5000 руб более мелкими купюрами. Друзья взяли по 1000 руб себе, а оставшиеся 2000 руб отдали другу на такси. Один из друзей стал рассуждать: «Каждый из нас потратил по 9000 руб, что в итоге составляет 27000 руб. Затем 2000 руб отдали на такси, значит, в итоге получается 29000 руб. Куда пропали 1000 руб?»
Решение:
Основной «подвох» в этом рассуждении заключается в том, что 2 От древнегреческого уловка.
расчеты сделаны неверно. Действительно, трое друзей сложились по 9000 руб и получили 27000 руб. Из этих денег 25000 руб заплатили за обед, а 2000 руб заплатили за такси. Следовательно, общая трата составила 27000 руб. Тс 2000 руб находятся внутри 27000 руб.
Пример:
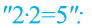
Сократим левую и правую часть последнего равенства на общий делитель (5-4-1). В итоге получим равенство 2-2=5.
Основной «подвох» в этом рассуждении заключается в том, что мы поделили обе части равенства 2-2-(5-4-1)=5-(5-4-1) на нуль.

Парадоксы, обычно, возникают в теориях, логические основы которых не определены полно.
Пример:
Парадокс лжеца. Рассмотрим высказывание «То, что я утверждаю сейчас — ложь».
Если это высказывание истинно, значит, исходя из его содержания, верно то, что данное высказывание -ложь. Но если оно -ложь, тогда неверно то, что оно утверждает, то есть утверждение о ложности данного высказывания неверно, значит, данное высказывание истинно. Таким образом, цепочка рассуждений возвращается в начало.
Пример:
Прилагательное русского языка назовем рефлексивным, если оно обладает свойством, которое определяет.
Например, прилагательное «русский» — рефлексивное, а прилагательное «английский» — нерефлексивное, прилагательное «трехсложный» — рефлексивное (это слово состоит из трех слогов), а прилагательное «четырехсложный» — нерефлсксивное (состоит из пяти слогов). Вроде бы ничто не мешает нам определить множество <все рефлексивные прилагательные>. Но давайте рассмотрим прилагательное «нерефлексивный». Оно рефлексивное или нет?
Можно заявить, что прилагательное «нерефлексивный» не является ни рефлексивным, ни нерефлексивным. Действительно, если это слово рефлексивное, то по своему смыслу, оно нерефлексивное. Если же это от древнегреческого 
Пример:
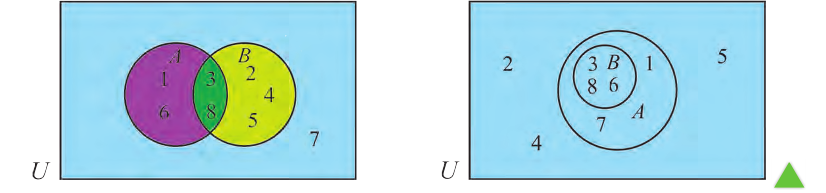
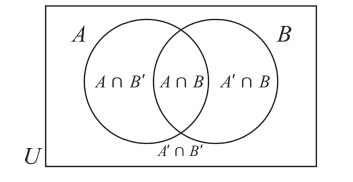
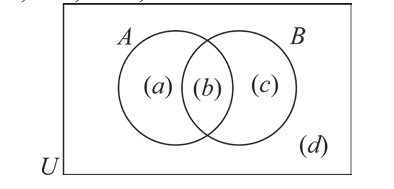
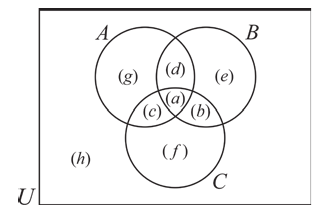
Два взаимно пересекающихся множества А, В делят универсальное множество на четыре части:
Следовательно, число элементов универсального множества является суммой количеств элементов этих частей.
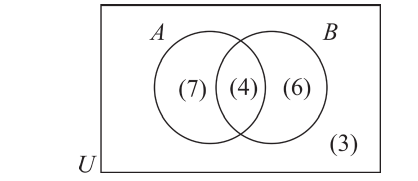
На следующей диаграмме мы заключили известные количества элементов частей универсального множества в круглые скобки:
Здесь, например, обоим множествам А, В принадлежат 4 элемента, а 3 элемента не принадлежат ни одному из них.
Так как произвольный элемент множества U, принадлежит только одному из этих 4 частей , то число элементов множества U равно 7+4+6+3=20.
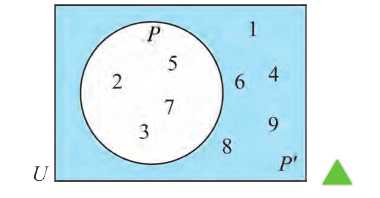
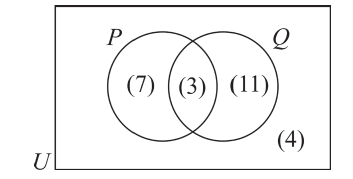
Пример:
Используя рисунок, найдите число элементов следующих множеств:
d). Множество элементов, принадлежащих Р, но не принадлежащих Q
е) Множество элементов, принадлежащих Q, но не принадлежащих Р;
f) Множество элементов, не принадлежащих ни Р, ни Q.
Пример:
Если
a) Найдите
b) Сколько элементов содержит множество элементов, принадлежащих А, но не принадлежащих В‘?
Решение:
Составим диаграмму Венна:
Из того, что 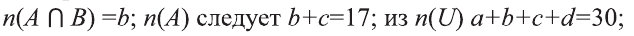
Из диаграммы получаем следующее:
b) Число элементов, принадлежащих А, но не принадлежащих В, равно а= 8
Пример:
Из 27 учеников, посещающих спортивную секцию, 19 имеют темные волосы, 14 — черные глаза, а 11 имеют и темные волосы и черные глаза одновременно.
a) Изобразите эту информацию с помощью диаграммы Венна. Объясните ситуацию.
b) Найдите число учеников, которые I имеют или темные волосы или черные глаза; II темноволосых, но не черноглазых?
Решение:
а) Пусть Qs — множество темноволосых, a Qk множество черноглазых учеников.
Изобразим ситуацию на диаграмме:
b) Используя диаграмму, определим следующее:
I количество учеников, имеющих или темные волосы или черные глаза:
II количество темноволосых учеников, не обладающих черными глазами:
Пример:
На футбольном соревновании город представляют три команды А, В и С. 20 процентов населения города болеют за команду И, 24 процента — за В, 28 процентов — за С. 4 процента жителей болеют и за С и за И, 5 процент, жителей болеют и за В и за А, а 6 процентов жителей болеют и за В и за С. Кроме того, 1 процент населения болеет за все три команды.
Сколько процентов жителей:
a) болеют только за команду А;
b) болеют и за А и за В, но не болеют за команду С;
c) не болеют ни за одну из команд?
Решение:
Заполним для начала соответствующую диаграмму Венна.
а= 1, так как 1 процент жителей болеет за все команды.
a+d=4, так как 4 процента жителей болеет и за И и за В.
а+b=6, так как 6 процентов жителей болеют и за В и за С а+с=5, так как 5 процентов жителей болеют
Множества
Понятие множества принадлежит к числу первичных, не определяемых через более простые. Под множеством понимается совокупность некоторых объектов, объединенных по определенному признаку. Объекты, которые образуют множество, называются элементами, или точками, этого множества.
Множества обозначаются прописными буквами, а их элементы — строчными. Если 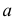
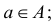
Например, 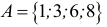
Множество, не содержащее ни одного элемента, называется пустым и обозначается 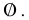
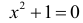
Два множества называются равными, если они состоят из одних и тех же элементов. Например, если 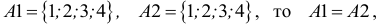
множества равны.
Объединением двух множеств А и В называется множество С, состоящее из элементов, принадлежащих хотя бы одному из данных множеств, т.е.
Пересечением двух множеств А и В называется множество D, состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств А и В, т.е.
Разностью двух множеств А и В называется множество E, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
Пример 1. Даны множества 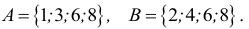
Решение. Объединение двух данных множеств — 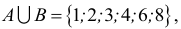
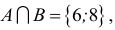
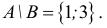
Множества, элементами которых являются действительные числа, называются числовыми.
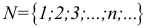
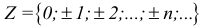
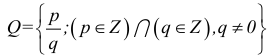
R — множество действительных чисел;
I — множество иррациональных чисел;
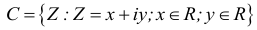
Геометрически, каждому действительному числу соответствует точка числовой оси, и наоборот, каждой точке прямой — определенное действительное число.
Множество X, элементы которого удовлетворяют: неравенству 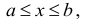
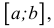
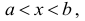
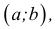
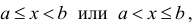
В дальнейшем все указанные множества мы объединяем термином промежуток X.
Множества и операции над ними
Под множеством будем понимать совокупность объектов, наделенных определенными свойствами. Эти свойства должны полностью определять данное множество, то есть являться признаками, по которым относительно любого объекта можно решить, принадлежит он данному множеству или нет. Синонимами термина «множество» являются термины «класс «семейство «совокупность». Объекты, из которых состоит данное множество, называют его элементами.
Чаще всего множество обозначают большими буквами латинского или греческого алфавита, а его элементы — малыми буквами. Если a — элемент множества A, то пишут a ∈ A (читают: «a принадлежит множеству A») или A 3 a (множество A содержит элемент a). Запись a ∈/ A означает, что a не является элементом множества A.
Множество обычно записывают одним из следующих способов:
Первая запись означает, что множество A состоит из элементов a, . . . , 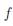
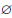
Определение 1.1. Множества A и B называются равными (или совпадающими), если они состоят из одних и тех же элементов, то есть x ∈ A тогда и только тогда, когда x ∈ B .
Коротко это высказывание записывают: A = B, а отрицание этого утверждения — в виде: 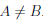
Определение 1.2. Если каждый элемент множества A является элементом множества B , то говорят, что A есть подмножество множества B (или A есть часть B ), и пишут A ⊂ B (читается: «Множество A содержится в множестве B») или B ⊃ A (читается: «Множестоо B содержит множество A»).
Отметим следующие свойства отношения включения:
1. A ⊂ A, то есть всякое множество есть подмножество себя самого;
2. Если A ⊂ B и B ⊂ C, то A ⊂ C (отношение включения транзитивно);
3. Если A ⊂ B и B ⊂ A, то A = B.
Удобно считать, что 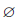
Пусть A и B — некоторые подмножества множества E. Введем наиболее простые операции с множествами.
Определение 1.3. Объединением множеств A и B называется множество, обозначаемое A ∪ B и состоящее из всех элементов, которые принадлежат или множеству A или B .
Таким образом, x ∈ A ∪ B , если x ∈ A, но x 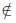
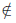
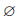
Определение 1.4. Пересечением множеств A и B называют множество, обозначаемое A∩B и состоящее из всех элементов, каждый из которых принадлежит и A и B .
Если множества A и B не имеют общих точек, то A ∩ B =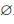
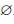
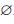
Определение 1.5. Разностью множеств A и B называют множество, обозначаемое A \ B и состоящее из всех элементов множества A, которые не принадлежат множеству B .
Если A ⊂ B , то часто множество A \ B называют дополнением множества B до A. По определению A \ A = 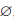
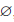
Пример 1.1. Пусть A = <1,3,4,8, 15>,B = <1,2,7,8, 12>. Тогда
Определение 1.6. Набор, состоящий из двух элементов x1 и x2, называют упорядоченным, если известно, какой из этих элементов является первым, а какой — вторым. Такой упорядоченный набор называют упорядоченной парой и обозначают (x1, x2). Элементы x1 , x 2 называют, соответственно, первой и второй координатами пары (x1, x2). Пары (x1, x2) и (y1 , y2) называют совпадающими, если x1 = y1 и x2 = y2 .
Определение 1.7. Декартовым (или, по-другому, прямым) произведением множеств A и B называют множество упорядоченных пар (x, y), где первый элемент x является элементом множества A, а второй y — элементом множества B . Это множество обозначают символом A × B .
Таким образом, A × B = < (x, y) | x ∈ A, y ∈ B>. Но, вообще говоря, A × B 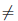
Пусть A и B — числовые отрезки, помещенные на взаимно перпендикулярных осях плоскости. Упорядоченная пара (x, y) — это точка пересечения перпендикуляров, восстановленных в точках x ∈ A и y ∈ B . Произведением A × B является прямоугольник.
Логическая символика
В последующем, как и в большинстве математических текстов используется ряд специальных символов, многие из которых вводятся по мере надобности. Применяются распространенные символы математической логики 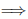
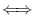
Запись A 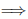
Запись A 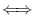
Запись «∃ x ∈ X » означает: существует элемент x из множества X .
Запись «∀ x ∈ X » означает: для любого элемента x из множества X или каков бы ни был элемент x из множества X .
Часто в символьной записи математических утверждений используют символ «:» или эквивалентный ему символ «| которые читают: «такой, что». В частности, запись «∃ x ∈ X : x 2 — 1 = 0» означает: существует такой элемент x в множестве X , что x 2 — 1 = 0.
Множества
Множества и операции над ними
Понятие множества и его элементов
Элемент 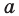
Элемент 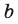
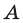
В множестве нет элементов
Множество можно представить как совокупность некоторых объектов, объединенных по определенному признаку. В математике множество — одно из основных неопределяемых понятий.
Каждый объект, принадлежащий множеству 
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается
Подмножество
Если каждый элемент множества 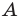
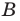
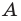
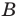
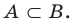
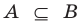
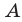
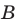
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества
Пересечение множеств
Пересечением множеств 
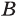

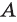
Объединение множеств
Объединением множеств 
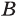


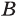
Разность множеств
Разностью множеств 
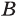


Если все рассматриваемые множества являются подмножествами некоторого универсального множества 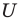




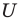
Объяснение и обоснование:
Понятие множества
Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты — элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы — ученики), множестве дней недели (элементы — дни недели), множестве натуральных делителей числа 6 (элементы — числа 1, 2, 3, 6) и т. д. В курсах алгебры и алгебры и начал анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество 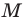
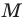
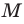
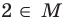
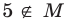
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например, множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом 
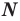

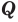
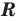
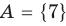
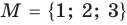
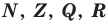
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило — характеристическое свойство, которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, множество 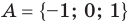
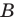

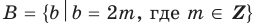
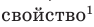
В общем виде запись множества с помощью характеристического свойства можно обозначить так: 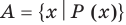
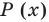
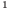
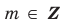
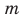
Равенство множеств
Пусть 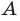
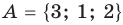
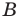
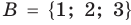
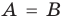
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, 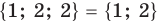
Подмножество
Если каждый элемент множества 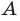
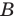
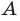
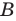
Это записывают следующим образом:
Например, 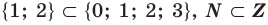
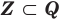
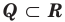
Полагают, что всегда 
Иногда вместо записи 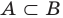
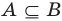
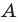
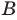
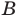
Сопоставим определение равенства множеств с определением подмножества. Если множества 




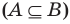



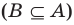
Таким образом, два множества равны, если каждое из них является подмножеством другого.
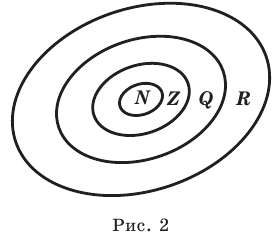
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера—Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами 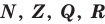
Операции над множествами
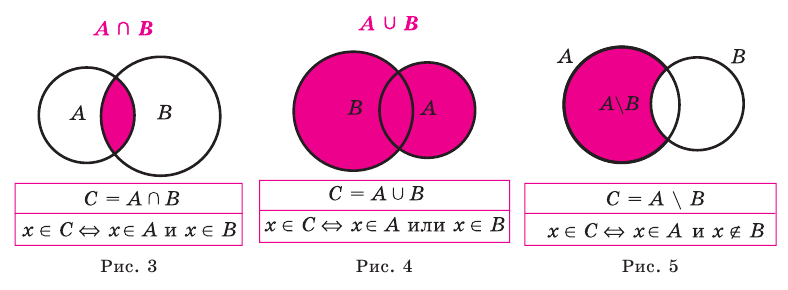
Над множествами можно выполнять определенные действия: пересечение, объединение, находить разность. Дадим определение этих операций и проиллюстрируем их с помощью кругов Эйлера—Венна.
Пересечением множеств 




Пересечение множеств обозначают знаком 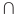
Например, если 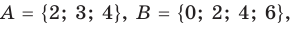
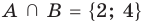
Объединением множеств 




Объединение множеств обозначают знаком 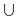
Например, для множеств 

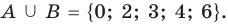
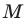
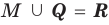
Разностью множеств 



Разность множеств обозначают знаком 
Например, если
Если 



Например, если обозначить множество всех иррациональных чисел через 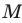
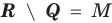
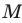
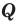
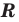
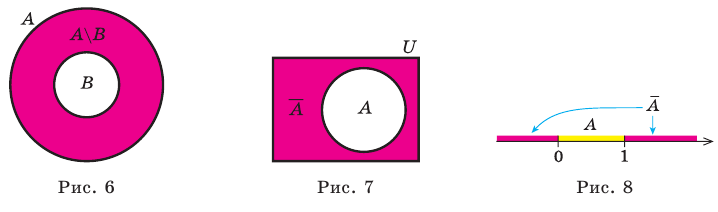
Если все множества, которые мы рассматриваем, являются подмножествами некоторого так называемого универсального множества 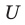
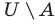
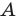
Дополнение множества 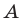
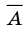
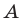
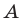
Например, если 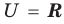
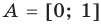
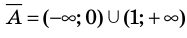
Числовые множества. Множество действительных чисел
Действительные числа
Числа, которые можно представить в виде бесконечной десятичной дроби
Рациональные числа
Можно представить в виде несократимой дроби 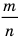
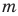
Нельзя представить в виде несократимой дроби 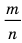
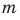
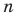
Целые числа
Включают натуральные числа, числа, противоположные им, и число нуль
Числа, состоящие из целого числа частей единицы
( 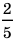
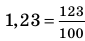
Натуральные числа 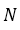
Для школьного курса математики натуральное число — основное не определяемое понятие
Такое число, при сложение с которым любое число не изменяется
Целые отрицательные числа
Числа, противоположные натуральным
Модуль действительного числа и его свойства
Определение:
Модулем положительного числа называется само это число, модулем отрицательного числа называется число, противоположное ему, модуль нуля равен нулю
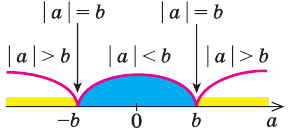
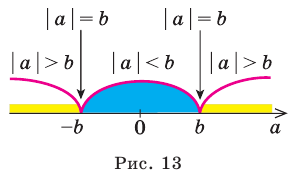
Геометрический смысл модуля
На координатной прямой модуль — это расстояние от начала координат до точки, изображающей это число.
Модуль разности двух чисел 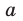
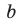
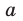
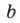
Свойства
1. 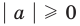
2. 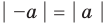
3. 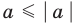
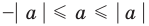
4. При
5. При
6. 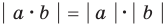
7. 
8.
9.
Модуль суммы не превышает суммы модулей слагаемых
10.
Объяснение и обоснование:
Числовые множества
В курсе математики вы встречались с разными числами: натуральными, целыми, рациональными, иррациональными, действительными. Представление о числах у человечества складывалось постепенно, под воздействием требований практики. Например, натуральные числа появились в связи с необходимостью подсчета предметов. Но для того чтобы дать ответ на вопрос «Сколько спичек в пустой коробке из-под спичек?», множества натуральных чисел 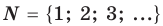
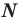
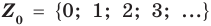
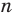
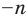
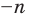
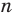
Натуральные числа, числа, противоположные натуральным, и число нуль составляют множество 
Измерение величин привело к необходимости расширения множества целых чисел и введения рациональных чисел. Например, средняя многолетняя температура воздуха в январе в г. Харькове — 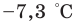
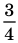
Таким образом, выбирая какую-либо единицу измерения, мы получаем числовое значение величин, которое может выражаться с помощью разных рациональных чисел — целых и дробных, положительных и отрицательных.
Целые и дробные числа составляют множество 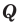
Любое рациональное число можно записать в виде дроби 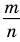
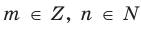
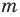
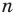
Рациональное число может быть записано разными дробями. Например,
Как видно из приведенных примеров, среди дробей, которые изображают данное рациональное число, всегда есть единственная несократимая дробь (для целых чисел — это дробь, знаменатель которой равен 1).
Обратим внимание, что рациональное число, записанное в виде дроби 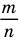
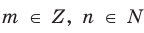
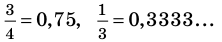
Договоримся, что конечную десятичную дробь можно изображать в виде бесконечной, у которой после последнего десятичного знака, отличного от нуля, на месте следующих десятичных знаков записываются нули, например, 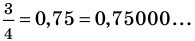
Целые числа также договоримся записывать в виде бесконечной десятичной дроби, у которой справа от запятой на месте десятичных знаков стоят нули, например 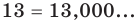
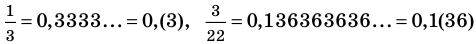
Таким образом, каждое рациональное число может быть записано в виде бесконечной периодической десятичной дроби и наоборот, каждая бесконечная периодическая дробь задает рациональное число.
Обратим внимание, что любая периодическая десятичная дробь с периодом девять равна бесконечной десятичной дроби с периодом нуль, у которой десятичный разряд, предшествующий периоду, увеличен на единицу по сравнению с разрядом первой дроби. Например, бесконечные периодические дроби 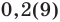
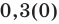
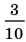
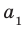
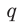
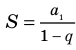
В дальнейшем, записывая рациональные числа с помощью бесконечных периодических десятичных дробей, договоримся исключить из рассмотрения бесконечные периодические дроби, период которых равен девяти.
Каждое рациональное число можно изобразить точкой на координатной прямой (то есть прямой, на которой выбраны начало отсчета, положительное направление и единица измерения). Например, на рисунке изображены несколько рациональных чисел 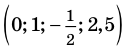
Однако на координатной прямой есть точки, изображающие числа, которые не являются рациональными. Например, из курса алгебры известно, что число 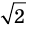
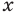
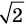
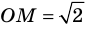
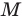
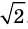
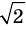
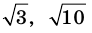
Рациональные и иррациональные числа составляют множество действительных чисел 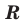
Каждое действительное число может быть записано в виде бесконечной десятичной дроби: рациональные числа — в виде бесконечной периодической десятичной дроби, а иррациональные — в виде бесконечной непериодической десятичной дроби.
Напомним, что для сравнения действительных чисел и выполнения действий над ними (в случае, когда хотя бы одно из них не является рациональным) используются приближенные значения этих чисел. В частности, для сравнения двух действительных чисел последовательно рассматриваем их приближенные значения с недостатком с точностью до целых, десятых, сотых и т. д. до тех пор, пока не получим, что какое-то приближенное значение одного числа больше соответствующего приближенного значения второго. Тогда то число, у которого приближенное значение больше, и считается большим. Например, если
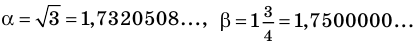
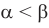
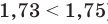
Для выполнения сложения или умножения рассмотренных чисел 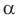
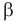
Как видим,
В курсе математического анализа доказывается, что в случае, когда приближенные значения чисел 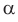
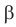
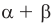
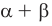
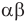
Модуль действительного числа и его свойства
Напомним определение модуля.
Модулем положительного числа называется само это число, модулем отрицательного числа — число, противоположное ему, модуль нуля равен нулю.
Это определение можно коротко записать несколькими способами. а при а > 0,
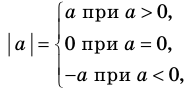
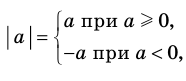
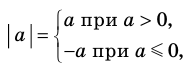
При необходимости мы будем пользоваться любой из этих записей определения модуля. Для нахождения 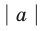
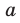
На координатной прямой модуль числа — это расстояние от начала координат до точки, изображающей это число.
Действительно, если 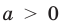
Если 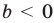
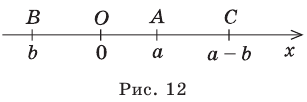
Модуль разности двух чисел 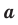
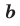
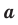
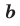
Для доказательства можно воспользоваться тем, что при параллельном переносе вдоль оси координат на 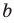
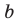
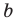
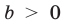
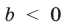
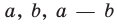
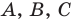

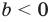
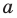
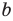
При параллельном переносе вдоль оси 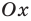
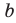
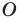
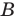
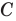
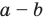
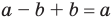
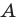
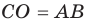
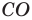
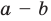
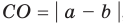
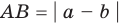
Используя определение модуля и его геометрический смысл, можно обосновать свойства модуля, приведенные в таблице 2.
Например, учитывая, что 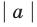
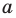
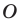
то есть модуль любого числа является неотрицательным числом.
Учитывая, что точки 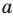
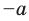
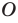
это означает, что модули противоположных чисел равны.
Если 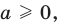
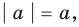
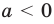
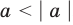
то есть каждое число не превышает его модуль.
Если в последнее неравенство вместо 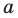
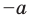
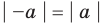
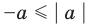
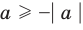
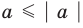

При 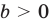

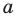
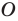
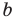
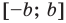
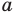
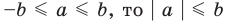
при 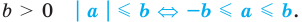
Обратим внимание, что последнее утверждение справедливо и при 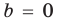
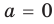
Аналогично при 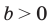
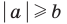
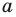
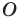
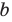
то есть в этом случае 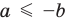
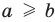
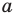
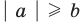

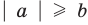

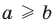
при
Свойства модуля произведения и модуля дроби фиксируют известные правила действий над числами с одинаковыми и разными знаками:
модуль произведения равен произведению модулей множителей, то есть
модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю), то есть
Формулу для нахождения модуля произведения можно обобщить для случая нескольких множителей
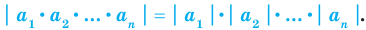
Если в формуле (3) взять 
Используя последнюю формулу справа налево при 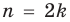
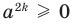
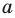
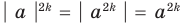
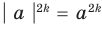
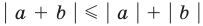
запишем неравенство (1) для чисел 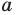
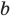
Складывая почленно эти неравенства, получаем
Учитывая неравенство (2), имеем

то есть модуль суммы не превышает суммы модулей слагаемых. Если в неравенстве (4) заменить 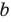
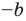
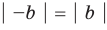
Если записать число 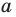
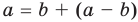
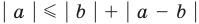

Если в неравенстве (6) заменить 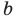
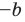
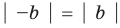

то есть модуль суммы двух чисел не меньше разности их модулей.
Меняя местами буквы 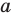
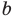
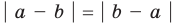

Полученные неравенства (4)-(8) можно коротко записать так:
Примеры решения задач:
Пример №402
Докажите, что сумма, разность, произведение, натуральная степень и частное (если делитель не равен нулю) двух рациональных чисел всегда является рациональным числом.
Решение:
► Пусть заданы два рациональных числа 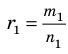
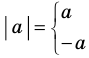
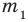
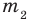
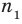
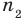
где 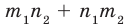
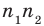
Любое рациональное число может быть записано как дробь 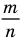
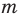
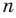
Чтобы доказать утверждение задачи, достаточно доказать, что сумма, разность, произведение и частное двух дробей вида 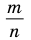
Пример №403
Докажите, что для любого натурального числа 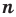
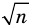
Для доказательства утверждения задачи можно использовать метод от противного: предположить, что заданное положительное число является рациональным ненатуральным (то есть дробью), и получить противоречие с условием или с каким-либо известным фактом.
Записывая 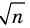
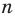
Решение:
► Допустим, что 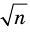
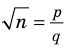
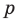
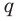
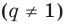
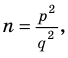
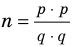
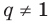
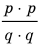
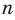
Следовательно, у натуральных множителей, которые стоят в числителе и знаменателе этой дроби, должен быть общий натуральный делитель, отличный от 1. Но в числителе стоят только множители 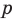
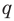

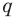
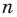
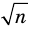
Например, поскольку числа 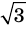
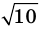
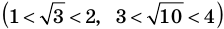
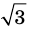
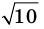
Пример №404
Докажите, что 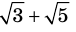
Решение:
► Допустим, что число 
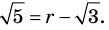
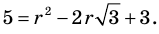
Следовательно,
Но правая часть этого равенства — рациональное число (поскольку по предположению 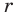
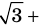
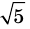
Для доказательства утверждения задачи можно использовать метод «от противного» — допустить, что заданное число является рациональным, и получить противоречие с каким-либо известным фактом, например с тем, что 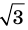
При анализе полученных выражений используем результат задачи 1: если число 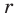
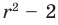
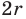
Заметим, что знаменатель полученной дроби
Пример №405
Решите уравнение
►
Ответ:
Заданное уравнение имеет вид 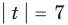
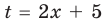
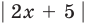
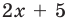
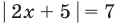
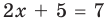
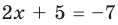
Ответ:
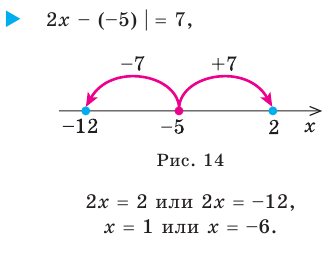
С геометрической точки зрения 
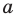
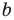
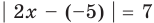
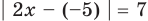
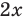
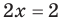
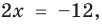
Пример №406
Решите неравенство
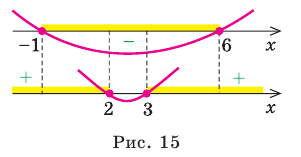
Решение:
Решая эти неравенства (рис. 15), получаем
Следовательно, 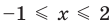
Ответ:
Заданное неравенство имеет вид 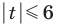
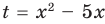
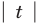
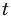
Тогда неравенству 
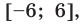
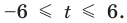
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Рациональные уравнения
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Функции, их свойства и графики
- Параллельность в пространстве
- Перпендикулярность в пространстве
- Векторы и координаты в пространстве
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Множество — виды, операции и примеры решения
Мы каждый день сталкиваемся с большим количеством одинаковых предметов, но не задумываемся о том, как называется совокупность этих объектов. Это множество — математическая единица, подчиняющаяся определенным законам и правилам, обладающая разными свойствами и функциями.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками < >.
А = <а, в, с, у>– А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N =
Выделяют три вида множеств:
конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
бесконечные — не являющиеся конечными (например, числовые);
пустые (обозначаются Ø) – не имеющие элементов.
Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.
Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
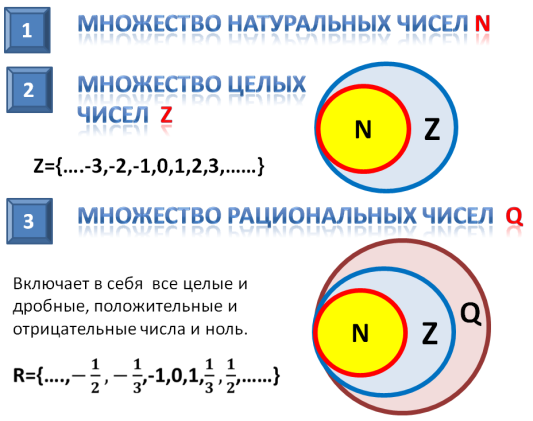
Множество натуральных чисел
К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.
Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
5 = 5/1 = 10/2 = 25/5;
0,45 = 45/100 = 9/20.
Следовательно, N и Z являются подмножествами Q.
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение
Пересечение
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
умножения S ∩ D = D ∩ S;
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
Транзитивность — законы включения:
если S ⊆ Fи F ⊆ J, то S ⊆ J;
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
О других свойствах операций можно узнать из картинки:
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно — несчетным. Другими словами, счетная единица — это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Теория множеств — достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.
http://www.evkova.org/mnozhestva
http://nauka.club/matematika/algebra/mnozhestvo.html