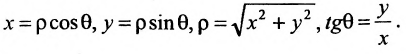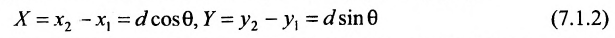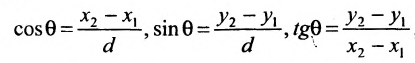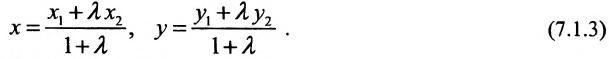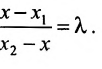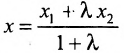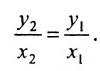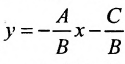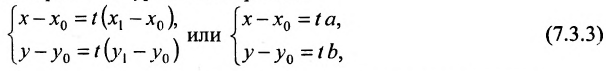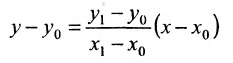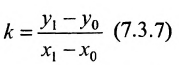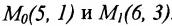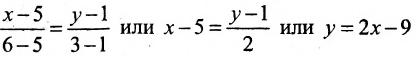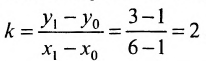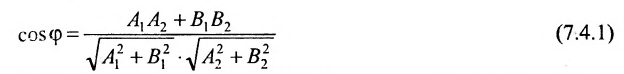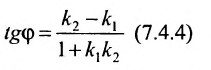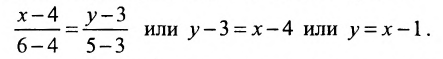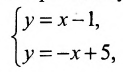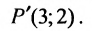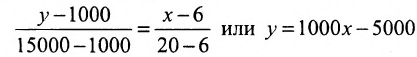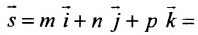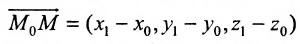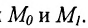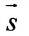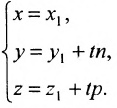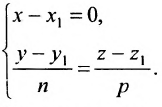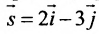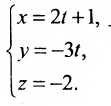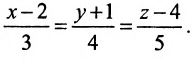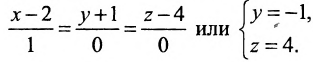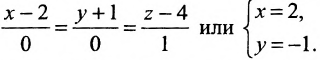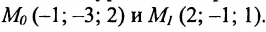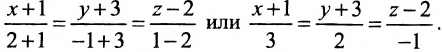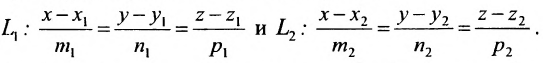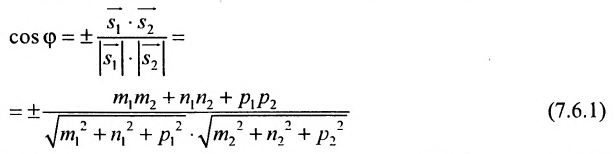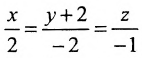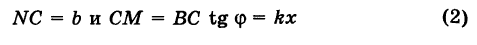Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
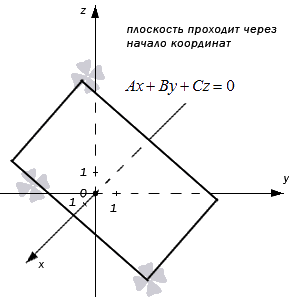
Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .
Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )
Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.
Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.
Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0
Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.
Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:
2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0
Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:
λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0
Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0
- Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:
M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0
Ответ: 3 x + 7 y — 5 z — 26 = 0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
- В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
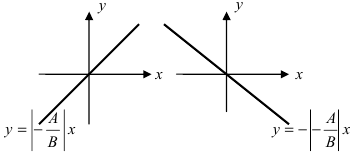
- Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.
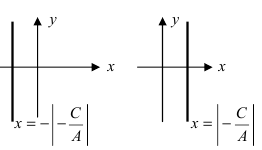
- При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0
Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0
Ответ: x — 7 = 0
Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .
Решение
Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .
Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .
Прямая линия на плоскости и в пространстве с примерами решения
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 — линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) — ему не удовлетворяет;
б)
в) 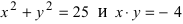
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 — уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
а) С = 0; 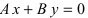
Рис. 20. Прямая, проходящая через начало координат.
б) 5 = 0; Ах+С=0 — прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
в) А = 0; Ву+С=0 — прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
Виды уравнений прямой
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 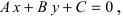
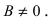
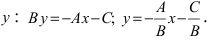
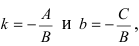
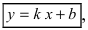
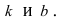
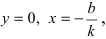
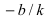
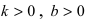
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 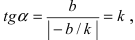
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 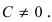
Обозначим через 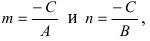
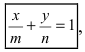
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 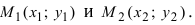
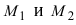
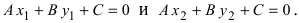
Пусть 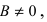
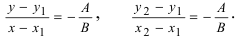
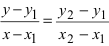
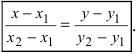
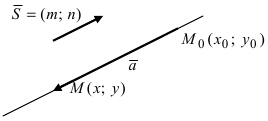
4. Уравнение прямой, проходящей через заданную точку 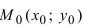
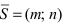
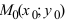
Определение: Вектор 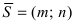
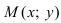
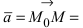
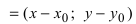
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 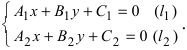
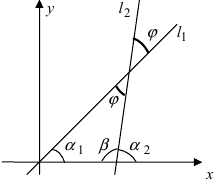
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что 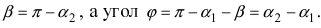
Наименьший угол между пересекающимися прямыми определим формулой 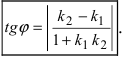
- а) если прямые
параллельны или совпадают
то
Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой
- б) если прямые
перпендикулярны
то
не существует.
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что 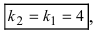
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты 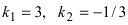
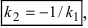
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 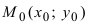
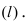
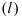
Если прямая 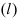
Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка 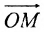
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая — второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси — координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую — осью ординат, обозначаемую Оу.
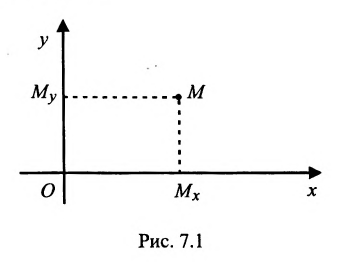
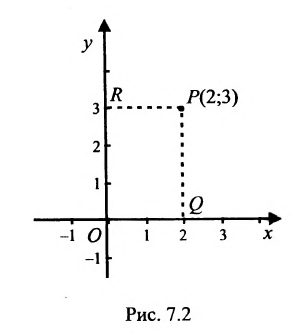
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно 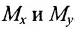
Координатами точки М в заданной системе называются числа 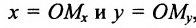
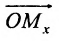
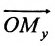
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у — М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
- первая координатная четверть: х>0, у>0;
- вторая координатная четверть: х
0, у>0;
- третья координатная четверть: х
0, у
0;
- четвертая координатная четверть: х>0, у
0.
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
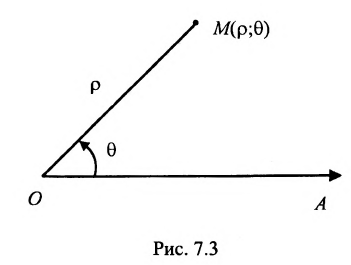
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат 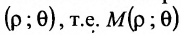
Декартова прямоугольная система координат связана с полярной системой формулами:
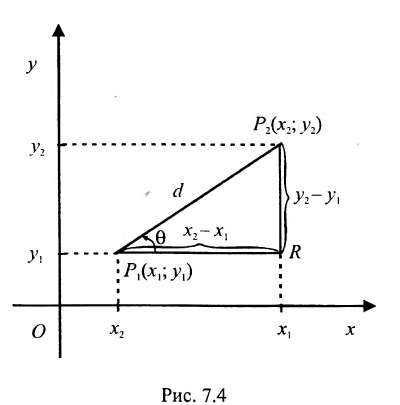
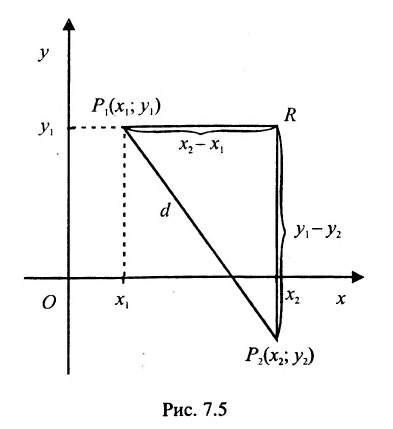
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками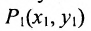
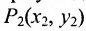
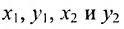
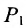
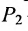
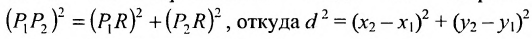
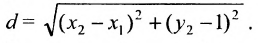
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки 
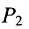
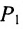
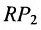
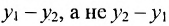
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как 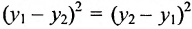
Если обозначить через 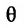
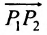
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u — произвольная ось, а 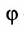
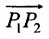
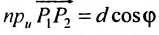
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая — второй. Обозначим их в заданном порядке через 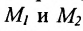
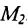
Определение 7.1.1. Число 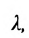
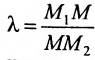
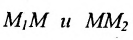
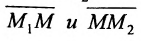
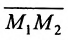
Число 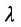
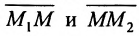
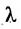
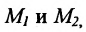
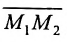
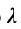
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек 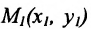
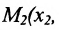
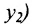
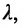
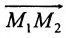
Решение задачи определяется следующей теоремой.
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок 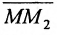
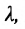
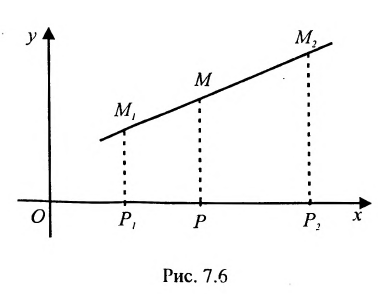
Доказательство:
Спроектируем точки 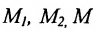
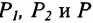
Подставив в (7.1.4) величины отрезков 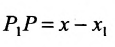
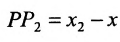
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если 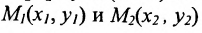
середина отрезка 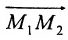
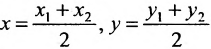
получаются из (7.1.3) при 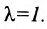
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора 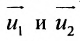
Для всех направляющих векторов 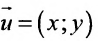
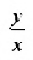
Действительно, если 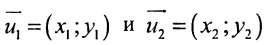
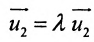
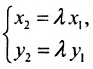
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
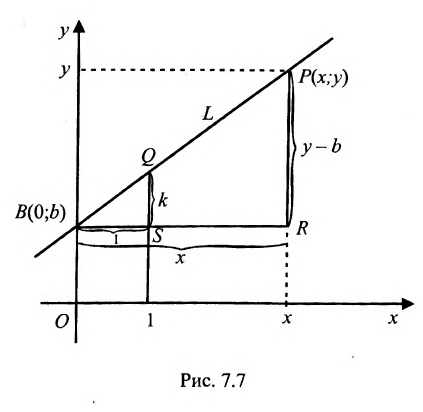
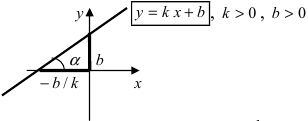
Доказательство: Пусть В = (О,b>- точка пересечения прямой L с осью у, а Р = (х,у) — любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р — прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то 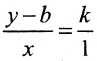
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
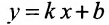
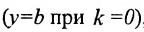
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Если 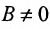
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
или 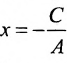
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как 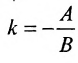
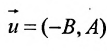
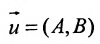
1. 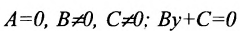
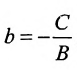
2. 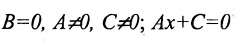
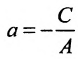
3. 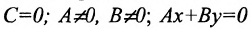
4. А=0; С=0; Ву-0 или у = 0 — это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 — это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где 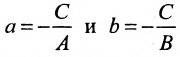
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки 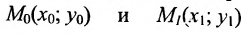
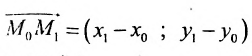
Геометрическое место концов всевозможных векторов вида 
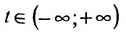
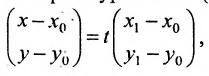
где 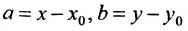
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
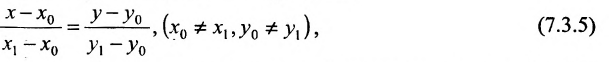
Если абсциссы точек 
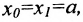
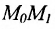
Если ординаты точек 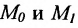
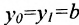
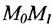
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку 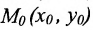
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек 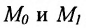
II способ. Зная координаты точек 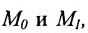
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: 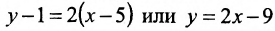
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
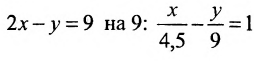
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями 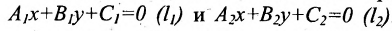
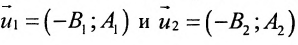
Если прямые параллельны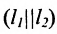
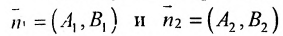
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые 
Например, прямые 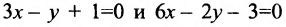
т. к.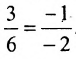
Если прямые перпендикулярны 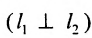
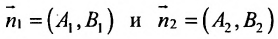
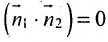
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые 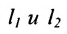
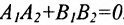
Например, прямые 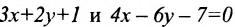
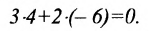
Если прямые заданы уравнениями вида 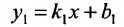
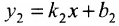
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
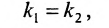
а для их перпендикулярности необходимо и достаточно, чтобы
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ — это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку 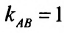
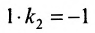
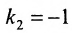
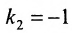
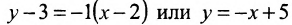
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
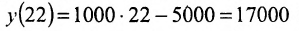
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: 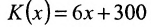
Прямая линия в пространстве
Системы координат в пространстве
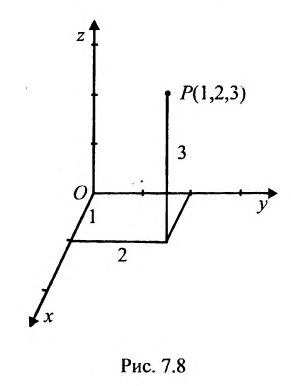
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
Пусть задано пространство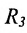
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки 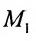
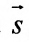
Вектор 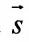
Итак, пусть прямая L проходит через точку 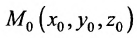
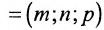
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор 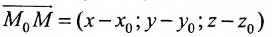
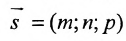
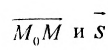
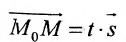
Уравнение 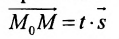
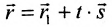
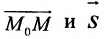
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками 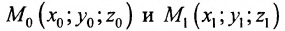
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где 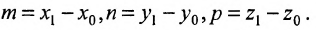
Пример:
Составить параметрические уравнения прямой, проходящей через точку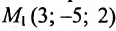
Решение:
В качестве направляющего вектора 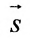
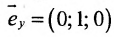
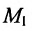
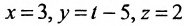
Пример:
Записать уравнения прямой 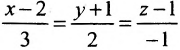
Обозначим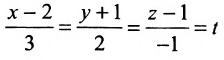
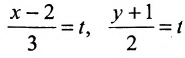
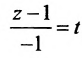
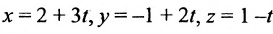
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде 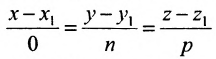
Аналогично, канонические уравнения
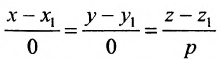
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку 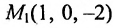
Решение:
Подставив координаты точки 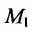
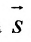
.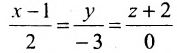
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой 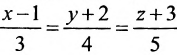
Решение:
а) Поскольку направляющий вектор заданной прямой
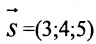
подставив координаты точки М(2; -1; 4) и вектора 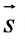
б) Поскольку единичный вектор оси О х: 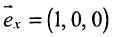
(7.5.3) координаты точки М(2; -1; 4 ) и вектора 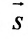
в) В качестве направляющего вектора 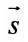
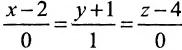
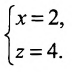
г) Единичный вектор оси Oz : 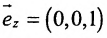
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек 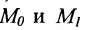
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол 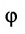
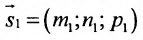
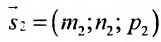
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов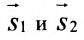
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. 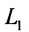
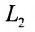
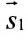
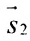
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми 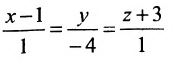
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов 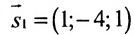
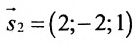
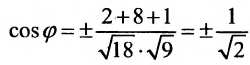
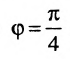
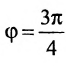
Вычисление уравнения прямой
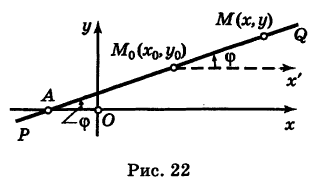
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х\ параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол 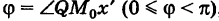
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала 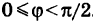
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
Нетрудно проверить, что формула (3) остается справедливой также и при х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Урок на тему «Метод областей». 11-й класс
Класс: 11
Презентация к уроку
«Считай несчастным тот день и тот час,
вк оторый ты не усвоил ничего нового и ничего
не прибавил к своему образованию».
Я.А Коменский
Тип урока: урок-обобщения и систематизации знаний учащихся.
Цели урока:
- создать условия для систематизации, обобщения знаний и умений обучающихся по применению различных методов решения неравенств;
- воспитание нравственных качеств личности, таких как ответственность, аккуратность, дисциплинированность;
- воспитание культуры общения.
- развитие у учащихся умений выделять главное, существенное в изучаемом материале, обобщать изучаемые факты, логически излагать свои мысли;
- развитие психических процессов, таких как память, внимание, мышление, а также наблюдательности, активности, самостоятельности.
Задачи:
- формировать умение классифицировать неравенства по методам решения;
- закрепить навыки решения неравенств различными методами;
- отрабатывать навыки самоконтроля с целью подготовки к итоговой аттестации;
- воспитывать чувство коллективизма, ответственности.
Оборудование:
- Компьютер
- Мультимедийный проектор, звуковые колонки
- Программа «MicrosoftPowerPoint 2003»
Методы обучения:
- частично-поисковый метод,
- репродуктивный,
- обобщающий.
План урока.
План урока рассчитан на 2 учебных часа (90 мин)
- Организационный момент.
- Вступительное слово учителя.
- Повторение теории.
- Решение неравенств различными методами (варианты ЕГЭ)
- Самостоятельная работа с самопроверкой.
- Итог урока.
- Рефлексия.
Ход урока
I. Организационный момент
«То, что мы знаем, — ограничено, а то чего
мы не знаем, — бесконечно».
Приветствие учащихся.Ученики под руководством учителя проверяют наличие дневника, рабочей тетради, инструментов, отмечаются отсутствующие, проверяется готовность класса к уроку, учитель психологически настраивает детей на работу на уроке.Формулируется тема и цели урока. Знакомство с этапами урока.
II. Вступительное слово учителя
Для успешного исследования многих задач повышенной сложности полезно уметь строить не только графики функций, но и множества точек плоскости, координаты которых удовлетворяют заданным уравнениям, неравенствам или их системам. Эффективно строить на координатной плоскости такие множества позволяет метод областей. Это весьма полезный прием можно назвать обобщающим методом интервалов.
Метод областей особенно полезен при решении уравнений или неравенств с параметром. Применение метода интервалов в таких случаях затруднено, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра. Это означает необходимость сравнивать их между собой и рассматривать различные случаи. В этой ситуации нам может помочь метод областей.
III. Повторение теории
Метод интервалов на координатной прямой и метод областей на координатной плоскости.
Точка х=а разбивает числовую прямую на два множества, задаваемые неравенствами x a
Всякая действительная кривая на координатной плоскости, заданная уравнением F(x;y)=0 разбивает координатную плоскость на конечное число областей, в каждой из которых для всех точек области выполняется только одно из неравенств: F(x;y)>0 или F(x;y) kx+p или y c
Решением системы неравенств с двумя переменными являются координаты точек пересечения множеств, удовлетворяющих одному из неравенств системы
Уравнение y= k(x-x0) + y0 задает множество прямых, проходящих через точку с координатами (x0,y0).
При изменении значений параметра прямые y= k(x-x0) + y0 «поворачиваются» вокруг данной точки. При увеличении параметра прямая поворачивается «против часовой стрелки», при уменьшении – «по часовой стрелке».
Уравнение y=kx+p при фиксированном значении параметра k = k0 задает семейство прямых, параллельных прямой y=kx+p проходящей через начало координат
Если точка с координатами 
Задача
Пусть M – множество точек плоскости с координатами (x; y) таких, что числа x, y, 6-2x являются сторонами некоторого треугольника. Найдите его площадь.
Если три числа являются сторонами некоторого треугольника, то это числа положительные и каждое из них меньше суммы двух других чисел. Поэтому, координаты точек, удовлетворяющих условию задачи, будут задаваться системой линейных неравенств с двумя переменными:
Геометрическое место точек на плоскости
Множество точек плоскости, равноудаленных от данной точки на расстояние, равное положительной величине R, называется окружностью.
Уравнением окружности называется уравнение вида
Множество точек, удаленных от данной точки на положительное расстояние, меньшее R, называется кругом. Круг задается неравенством
Множество точек, лежащих вне круга, задается неравенством
Геометрическое место точек на плоскости
Квадратным трехчленом относительно переменной, называется выражение
Графиком квадратного трехчлена является кривая, называемая параболой.
Расположение параболы зависит от знака старшего коэффициента и знака дискриминанта квадратного трехчлена
Парабола разбивает плоскость на часть, лежащую «над» параболой и лежащую «под» параболой. Первая задается неравенством
, а вторая –
Метод областей при решении задач с параметрами
1. Свойства функций
2. Графический прием
Параметр – «равноправная» переменная Þ отведем ему координатную ось, т.е. задачу с параметром будем рассматривать как функцию f(x ;a) >0
Общие признаки задач подходящих под рассматриваемый метод:
- В задаче дан один параметр а и одна переменная х
- Они образуют некоторые аналитические выражения F(x;a), G(x;a)
- Графики уравнений F(x;a)=0,G(x;a)=0 строятся несложно
- Строим графический образ
- Пересекаем полученный график прямыми, перпендикулярными параметрической оси
- «Считываем» нужную информацию
Обобщенный метод областей («переход» метода интервалов с прямой на плоскость)
Неравенства с одной переменной
Неравенства с двумя переменной
- ОДЗ
- Граничные линии
- Координатная плоскость
- Знаки в областях
- Ответ по рисунку
IV. Решение неравенств
Пример №1
Найти все значения параметра p, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства
Применим обобщенный метод областей.
1. Построим граничные линии
2. Определяем знаки в полученных областях и получаем решение 1 неравенства
3. Из полученного множества исключим решение
Пример № 2
При каких значениях параметра а система неравенств не имеет решений.
1. Рассмотрим 1 неравенство и получаем
2. Рассмотрим 2 неравенство и получаем
3. Заметим, что исходная система неравенств равносильна системе:
4. Изобразим систему неравенств в виде плоской фигуры на координатной плоскости. Для этого введём параметрическую плоскость Oax
5. Мы получили плоскую фигуру, множество точек которой является решением системы.
Таким образом, отвечая на вопрос задачи, решений системы нет при
Пример №3
При каких положительных значениях параметраа система уравнений имеет ровно 4 решения.
1. Запишем систему в следующем виде:
2. Построим график 1 уравнения.
3. Построим график 2 уравнения – семейство окружностей с центром в точке (2; 0) и радиусом а.
Ответ: при
V. Самостоятельная работа с самопроверкой
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству
1. ОДЗ:
2. Строим граничные линии:
3. Они разбивают плоскость на восемь областей, определяя знаки подстановкой в отдельных точках, получаем решение.
Ответ: заштрихованная область на рисунке
На координатной плоскости изобразите множество точек, координаты которых удовлетворяют неравенству
- На координатной плоскости нарисуем линии определённые равенствами x-y=0 и xy-1=0, которые разбивают плоскость на несколько областей.
- Определяем знаки в областях.
Ответ: заштрихованная область на рисунке
VI. Итог урока
(подвожу итог, комментирую работу учащихся, сообщаю оценки за урок.)
VII. Рефлексия.
Ребята. На этом урок окончен. Спасибо за урок!
Литература.
- П. И. Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. 3-е издание, дополненное и переработанное. — М.: Илскса, Харьков: Гимназия, 2005,- 328 с.
- Черкасов О. Ю., Якушев А. Г. Математика: интенсивный курс подготовки к экзамену.
- Экзаменационные материалы для подготовки к ЕГЭ-2007. Математика. М.: ООО «РУСТЕСТ», 2006. — 108с. Сост. — Клово А.Г.
- Задачи с параметром и другие сложные задачи. Козко А.И., Чирский В.Г. М.: МЦНМО, 2007. — 296с.
- ЕГЭ 2011. Математика. Задача С5. Козко А.И., Панферов В.С., Сергеев И.Н., Чирский В.Г.
http://www.evkova.org/pryamaya-liniya-na-ploskosti-i-v-prostranstve
http://urok.1sept.ru/articles/664756


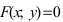
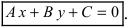
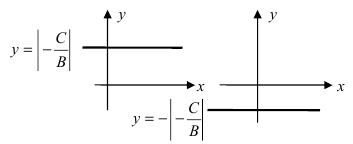
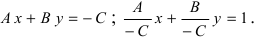
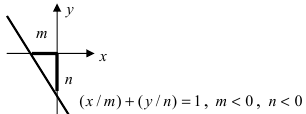
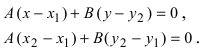
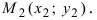
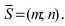
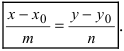
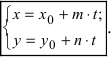
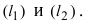
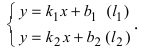
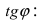
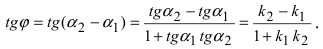
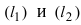 параллельны или совпадают
параллельны или совпадают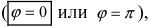 то
то 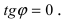 Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой
Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой 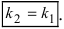
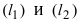 перпендикулярны
перпендикулярны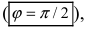 то
то 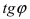 не существует.
не существует.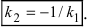
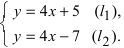
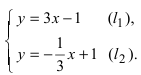
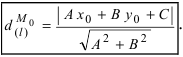
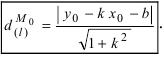
 0, у>0;
0, у>0; 0, у
0, у 0;
0; 0.
0.